Mathematics Grade 11 EUCLIDEAN GEOMETRY Presented By Avhafarei

Mathematics Grade 11 EUCLIDEAN GEOMETRY

Presented By Avhafarei Thavhanyedza Saint Georges Conference Centre 03 March 2017

TOPIC OVERVIEW 1: Revise Grade 10 work & earlier grades 2. Concepts learnt from earlier grades (and tan-chord theorem) must be used as axioms 3. Use theorems & their converses to solve riders

Proof theorems for Circle Geometry The line drawn from the centre of a circle perpendicular to a chord, bisects the chord (┴ from centre) The Perpendicular bisector of a chord passes through the centre of a circle The angle subtended by an arc at the centre of the circle is double the size of the angle subtended by the same arc at the circumference (angle at centre = 2 angle at circum)

Proofs of theorems (Cont ---) Angles subtended by a chord of a circle on the same side of the chord are equal The opposite angles of a cyclic quad are supplementary (opp angle cyclic quad) Two tangents from the same point are equal in length (2 tan to circle) The angle between tangent & chord = the angle in the alternate segment (tan-chord theorem)

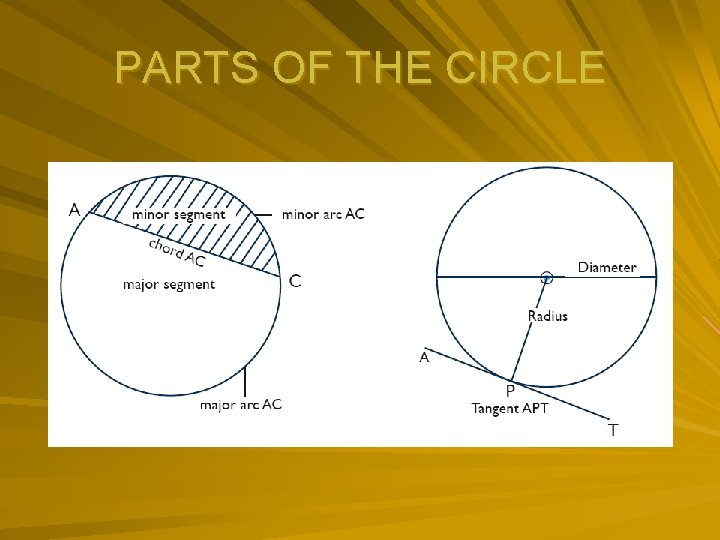
PARTS OF THE CIRCLE

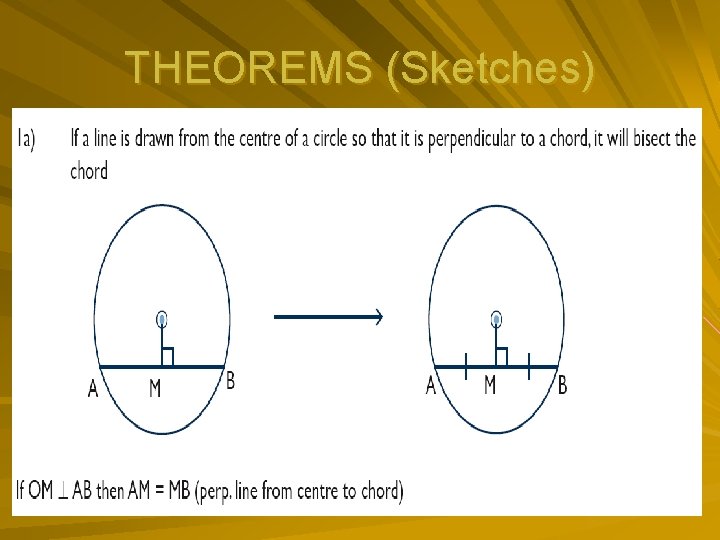
THEOREMS (Sketches)

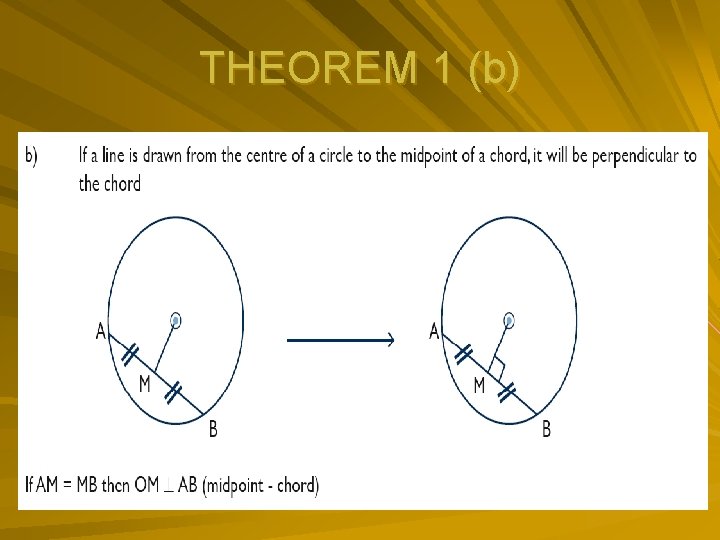
THEOREM 1 (b)

ANGLE AT CENTRE THEOREM

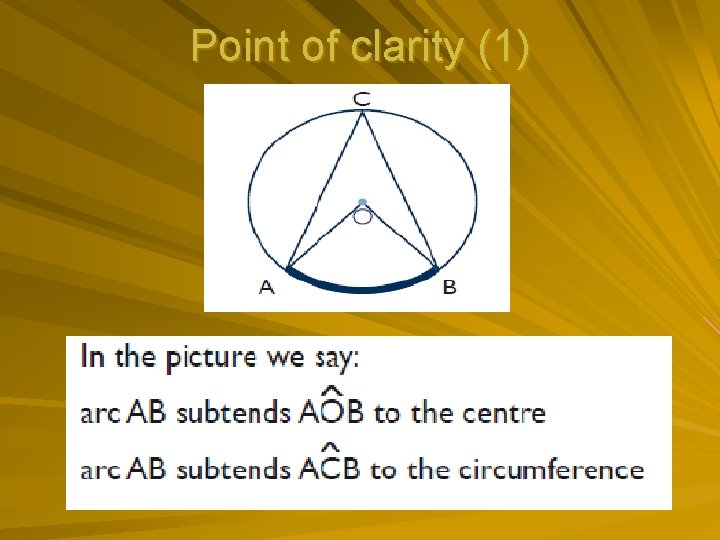
Point of clarity (1)

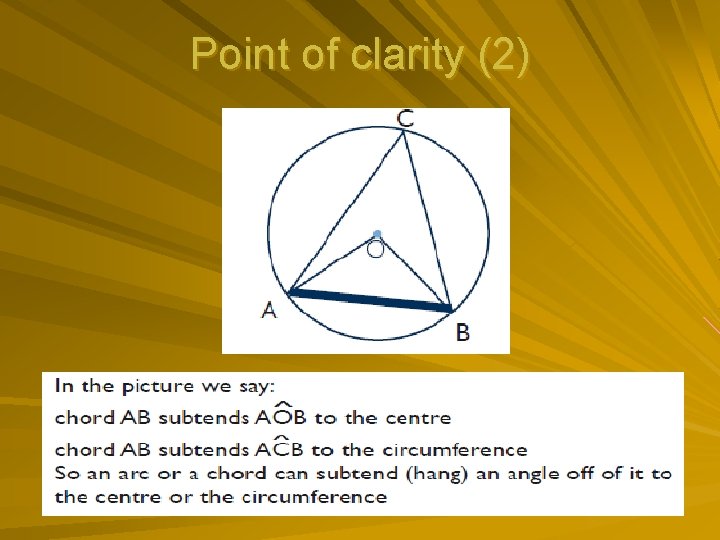
Point of clarity (2)

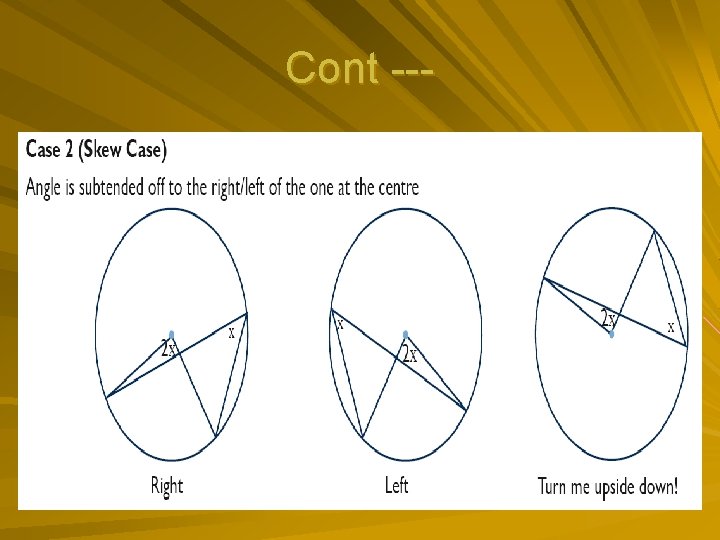
Cont ---

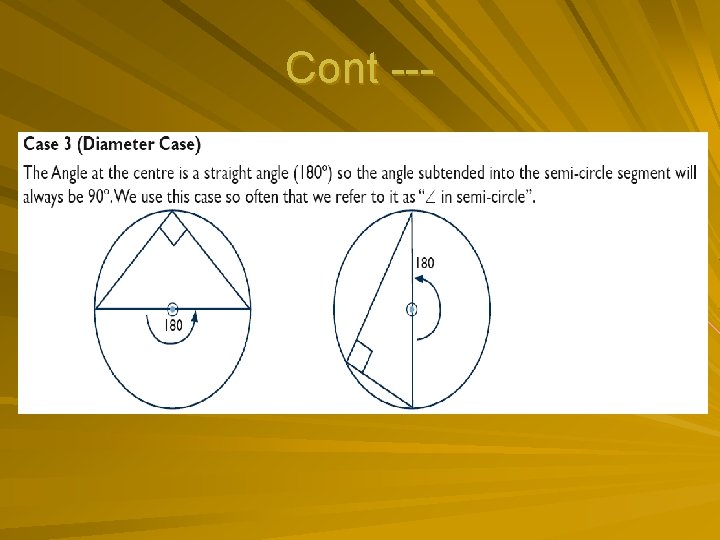
Cont ---

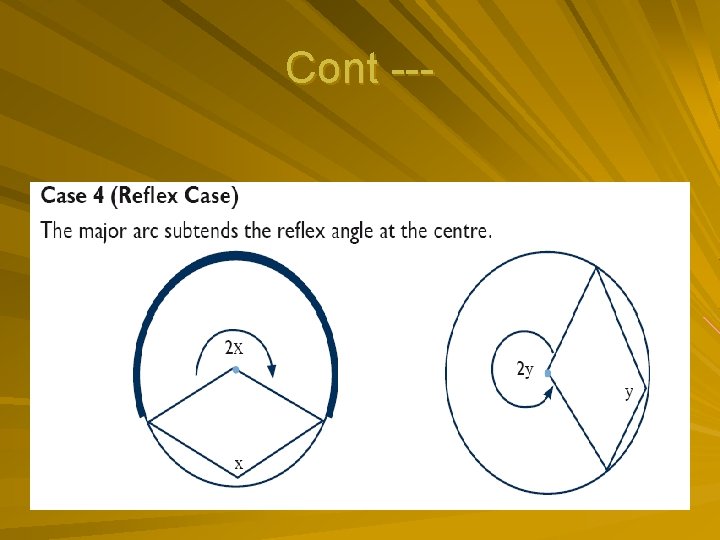
Cont ---

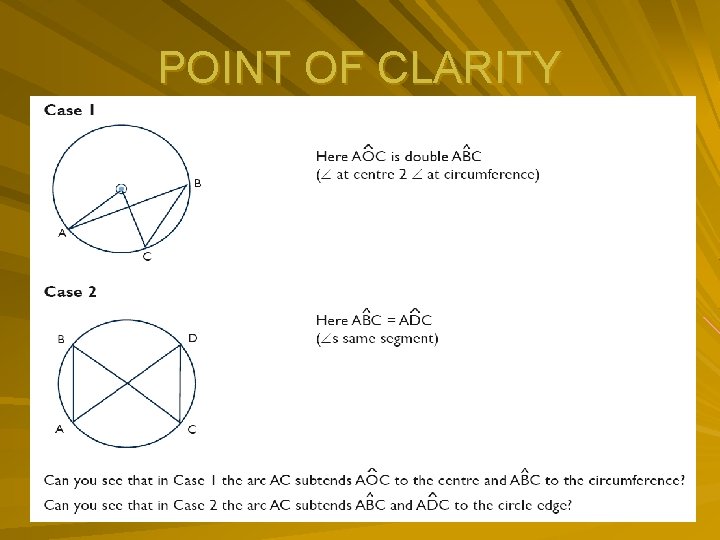
POINT OF CLARITY

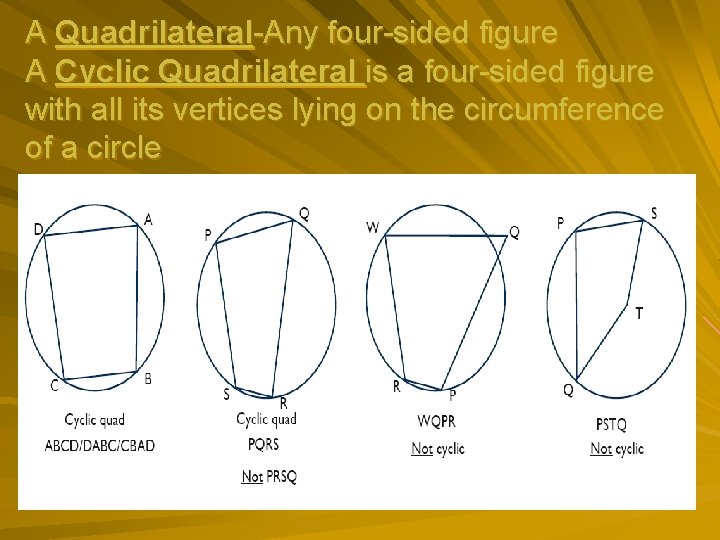
A Quadrilateral-Any four-sided figure A Cyclic Quadrilateral is a four-sided figure with all its vertices lying on the circumference of a circle

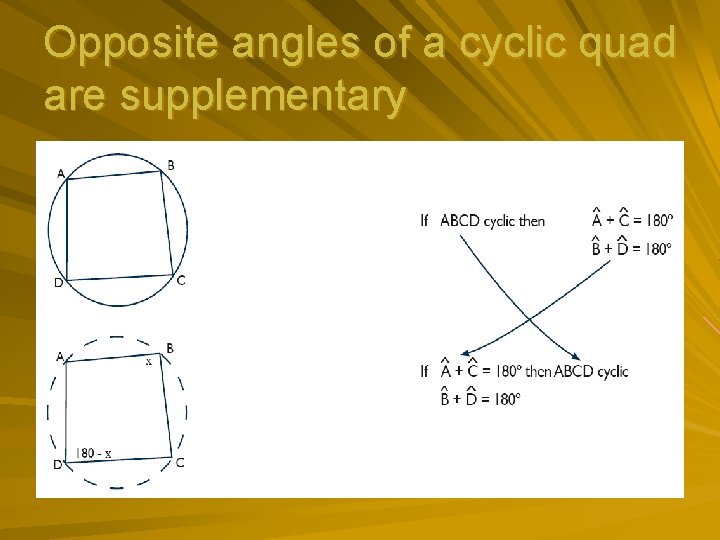
Opposite angles of a cyclic quad are supplementary

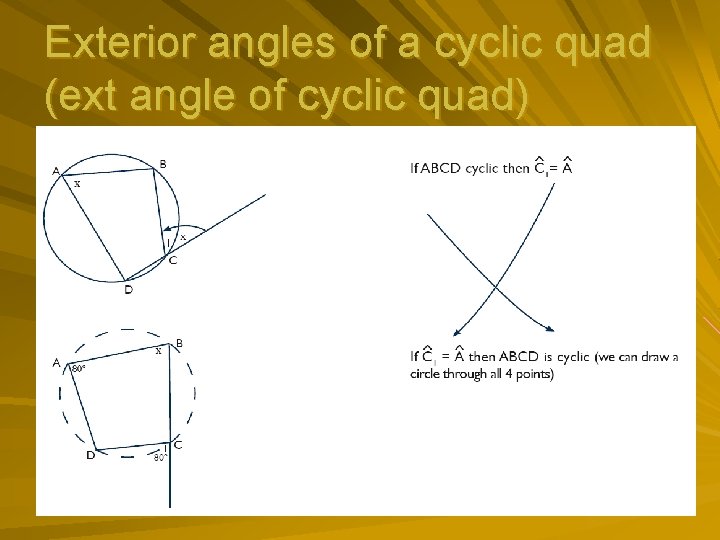
Exterior angles of a cyclic quad (ext angle of cyclic quad)

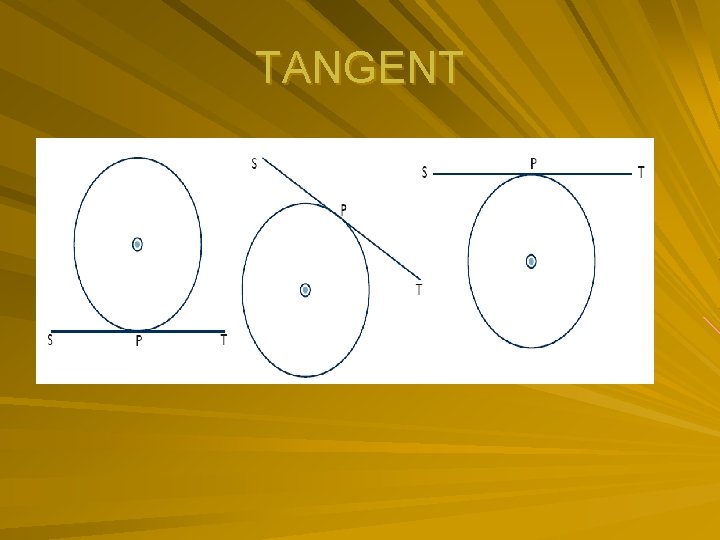
TANGENT

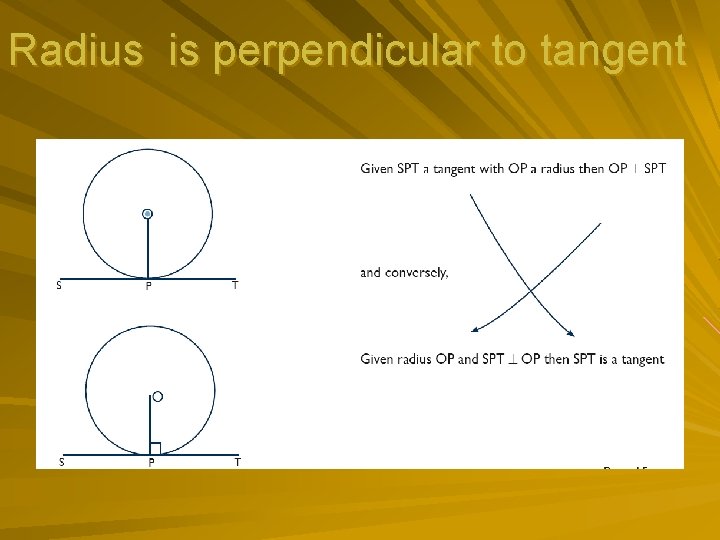
Radius is perpendicular to tangent

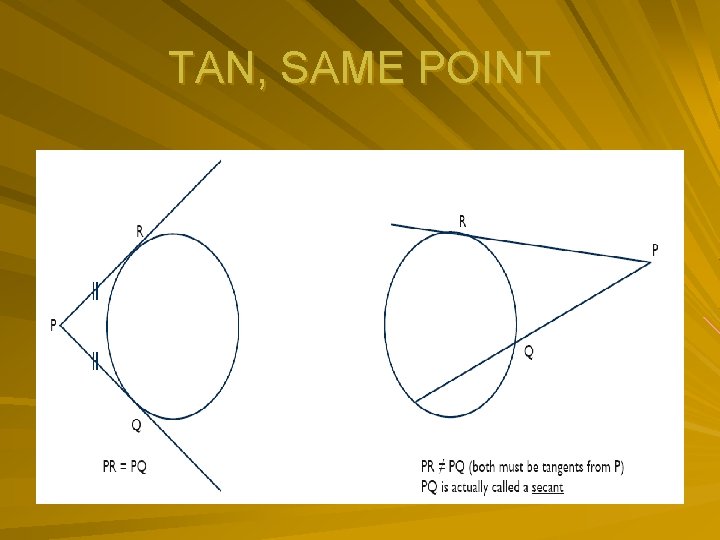
TAN, SAME POINT

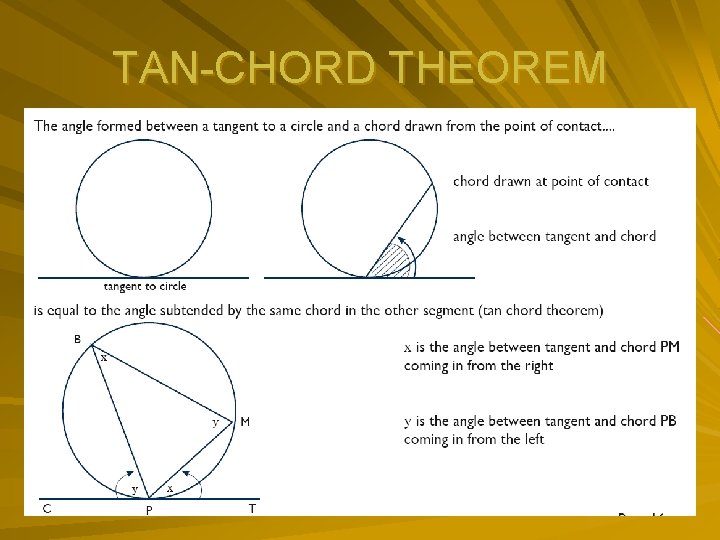
TAN-CHORD THEOREM

Hints in solving problems Use x and y on the diagram Mark all equal angles with x’s and y’s and try to solve the problem Use colours on the diagram Mark equal angles with red open dots, red closed dots, blue stars, etc

STEPS IN SOLVING RIDERS

General advice for solving riders Highlight all parallel lines in the same colour, to find alternate and corresponding angles equal. Use suitable markers to mark angles equal to each other in the same colour. Look at what you are required to prove, and select a strategy to solve the problem.

Cont --Make a preliminary test to see if your strategy has a chance of success. Always re-check the given to make sure that you have used ALL the given information. Look at previous parts of questions for clues. You may need to further extend the solutions or conclusions to these questions.

Centre of the circle: Mark off all radii- and consequently, all base angles of isosceles triangles formed by radii, equal. If given that a chord is bisected- mark off the 90° angle formed by the perpendicular line from the centre of circle. For all diameters, mark off angles subtended at the circumference equal to 90°. Check each angle at the centre (mark it as 2 x) and mark off the angle at the circumference as x (using x may be cumbersome). Mark the 90° angle formed between radius and tangent, if you are given a tangent.

TANGENT Mark off all radii perpendicular to tangent. Check if any two tangents come from the same point, and mark them equal, (also mark off the base angles of isosceles triangle formed as a result). Mark the angle between the tangent and chord and the angles that they will be equal to in the alternate segment.

CYCLIC QUADRILATERAL Remember you may not always be told that quadrilaterals in a given circle are cyclic. You would have to check the circle in your diagram to see if there are four or more points on the circle forming cyclic quadrilaterals. Mark off all angles in the same segment equal. Mark off all exterior angles = to interior opposite angles. Remember that opposite angles of cyclic quad. are supplementary. Work backwards from the 'required to prove'

If asked to prove two line segments equal: If they are in the same triangles try proving the base angles of that triangle equal (i. e. the angles opposite the sides you want to prove equal. ) If they are in two different triangles - check to see if triangles are congruent. Check if the angles subtended by the chords are equal, or if you can prove them equal.

If asked to prove two angles equal If they are in the same triangle, check to see if these angles are the base angles of an isosceles triangle - are the sides equal. If you are trying to prove ÐA = ÐB, then find all angles equal to , and all angles equal to ÐA, and all angles equal to ÐB; now check if there is an angle equal to both ÐA & ÐB.

USING AL ALGEBRAIC APPROACH Sometimes you may need to prove an equation that has some numerical value in it: e. g. ÐA = 90° – 2ÐB This may require you to start with an equation that already has a numerical value: e. g. Sum of angles of triangle equal to 180°. Opposite angles of cyclic quad are supplementary. Co-interior angles are supplementary. Manipulate the relevant numerical equation using substitution of equal quantities to arrive at the required equation.

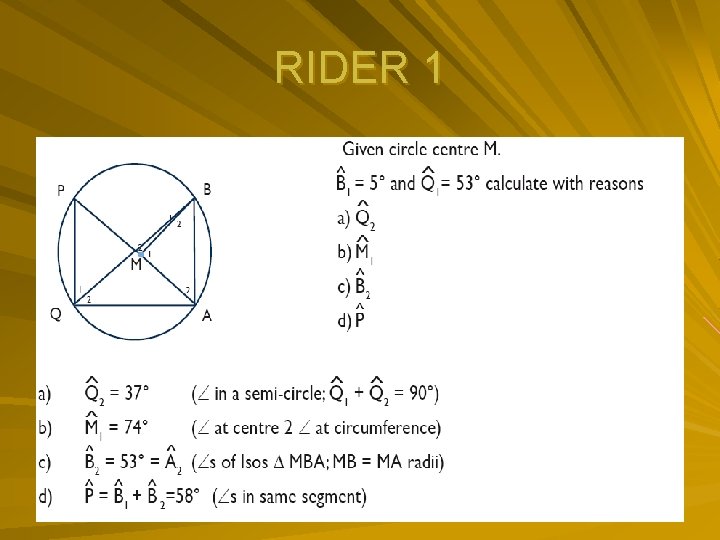
RIDER 1

RIDER 2

SOLUTION 1

SOLUTION 2

Hints in examinations Proofs of theorems can be asked in examinations, but their converses cannot be asked.