Modelos dos Processos Fisiolgicos no Homem DIN MICAS

Modelos dos Processos Fisiológicos no Homem DIN MICAS POPULACIONAIS COM CAOS Emeline Alves Hugo Tavares Ricardo_Couceiro@yahoo. com. br Ricardo Couceiro Samuel Pereira Faculdade de Ciências e Tecnologia da Universidade de Coimbra

Dinâmica de Populações Descrição do número de indivíduos de uma população ao longo do tempo, o qual é uma variável que pode ser representada discreta ou continuamente.

§ § A Dinâmica de Populações é uma importante síntese matemática que permite identificar e estudar diversas teorias da Biologia Teórica: nível molecular em Processos Físicoquímicos nível celular em Fisiologia Epidemiologia Sociobiologia de organismos superiores

Neste trabalho vamos abordar modelos de sistemas lineares e não lineares, dando maior importância aos sistemas não lineares com caos. Os sistemas lineares caracterizam-se por depender apenas de um factor constante.

Modelo de Malthus A premissa básica deste modelo consiste “na taxa na qual uma população cresce ser directamente proporcional ao seu tamanho". Para criar esse modelo, serão utilizadas várias variáveis: § T – tempo decorrido desde o início da experiência. § P – tamanho da população no tempo T.

A taxa de mudança da população, ou a taxa de crescimento, é representada pela quantidade d. P/d. T ou. Introduzidas estas quantidades, a ideia de Malthus é: k- é a diferença entre a taxa de natalidade e a taxa de mortalidade. • se k > 0, a população é crescente. • se k < 0 a população decai ao longo do tempo. • se k=0 a população permanecerá constante no tempo (a taxa de natalidade é igual à taxa de mortalidade).

Quando T=0 a população é. Assim, a condição inicial é P(0)=. Introduzindo isso na equação diferencial original, obtemos: Integrando:

Assumimos taxas de natalidade e mortalidade constantes o que simplificou ainda mais o modelo, no entanto, no mundo real, não o são. Portanto a função P(T) que obtemos é uma aproximação contínua da população, a qual aumenta por números inteiros. Este modelo não é muito realístico, pois, na verdade, k é raramente uma constante, já que pode depender de vários factores, como: § fertilidade § saúde da população § nutrientes disponíveis, etc. , os quais têm relação directa com as taxas de natalidade e de mortalidade.

O modelo Malthusiano descreve com razoável aproximação o crescimento da espécie humana. Contudo, estudos de crescimento populacional em laboratório e na natureza mostram que as populações podem crescer exponencialmente durante um curto intervalo de tempo até um determinado limite, inerente às circunstâncias da natureza.

Modelos de sistemas não lineares • Modelo de Verhulst ou de Beverton & Holt • Modelo Logístico • Modelo de Ricker

Modelo de Verhulst • Deriva do modelo de Malthus Considerar: • Estirpe de bactérias que depende de histidina para se reproduzir • Reproduz-se de a cada 40 minutos (condições ideais)

• Com falta de histidina os ciclos são maiores Seja, Então, • K – constante de saturação ou nível de substrato

Como solucionar o modelo anterior § Iterações analíticas § Iterações geométricas § Métodos de simulação computacional

Iterações analíticas § Seja, § Então, § Através de substituições recursivas obtemos a equação:

§ Podemos concluir que: logo, § A população tende para o valor K

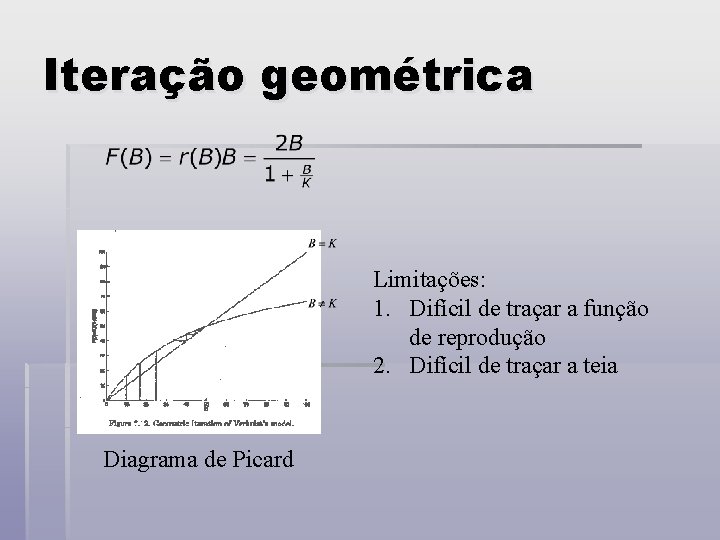
Iteração geométrica Limitações: 1. Difícil de traçar a função de reprodução 2. Difícil de traçar a teia Diagrama de Picard

Modelo de Verhulst com predação § É implementado um predador no sistema § População não depende só do factor “meio” Seja, Então o modelo será,

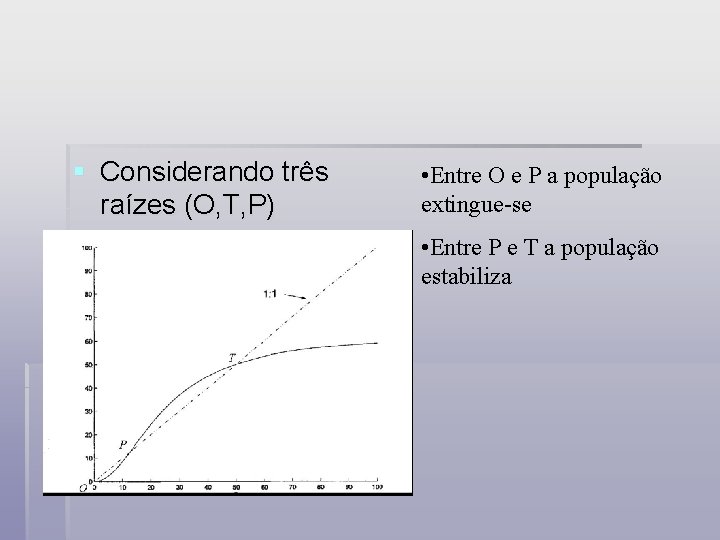
§ Considerando três raízes (O, T, P) • Entre O e P a população extingue-se • Entre P e T a população estabiliza

Dinâmicas Populacionais com Caos SISTEMAS NÃO LINEARES Modelo Logístico

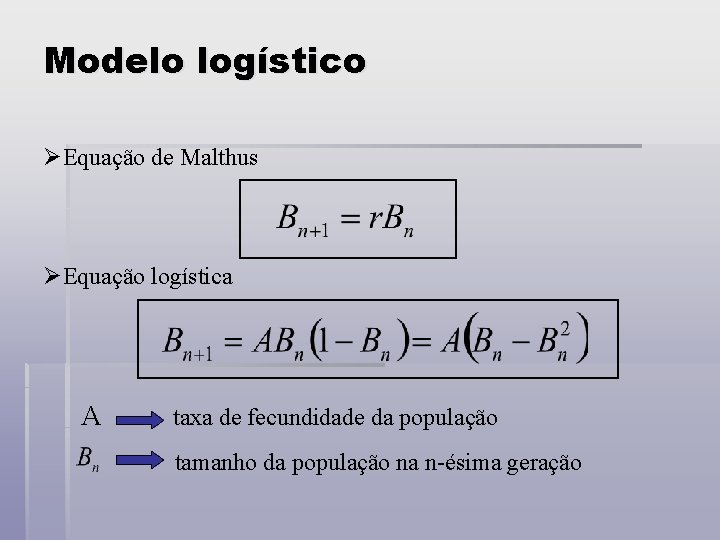
Modelo logístico ØEquação de Malthus ØEquação logística A taxa de fecundidade da população tamanho da população na n-ésima geração

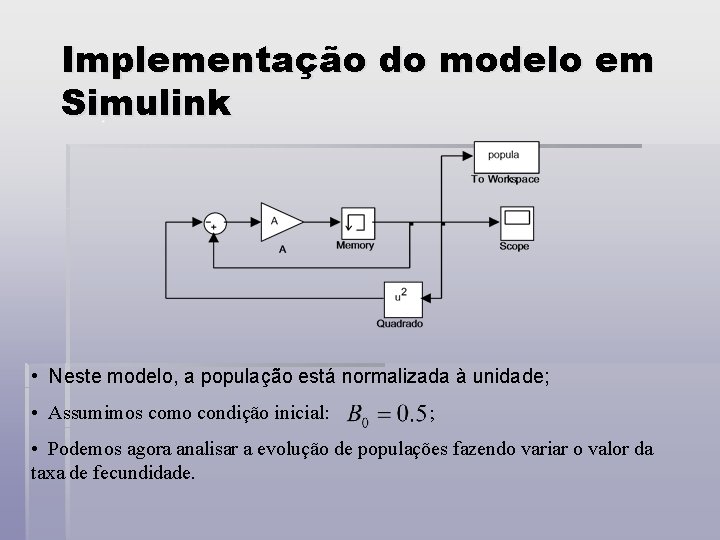
Implementação do modelo em Simulink • Neste modelo, a população está normalizada à unidade; • Assumimos como condição inicial: ; • Podemos agora analisar a evolução de populações fazendo variar o valor da taxa de fecundidade.

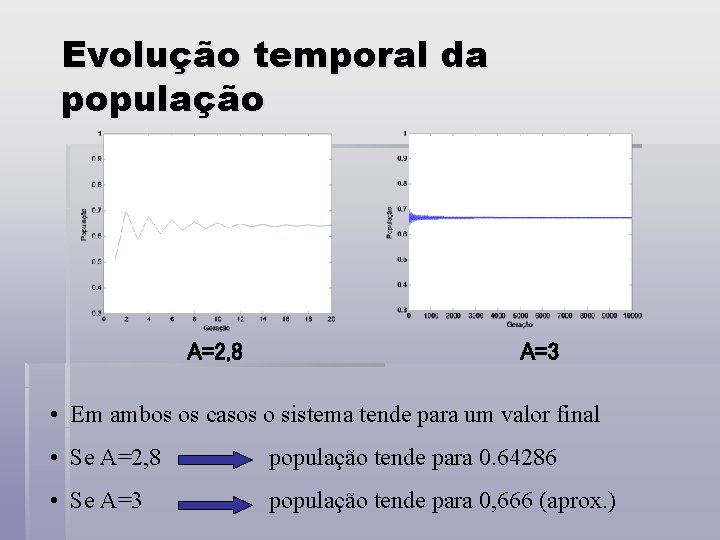
Evolução temporal da população A=2, 8 A=3 • Em ambos os casos o sistema tende para um valor final • Se A=2, 8 população tende para 0. 64286 • Se A=3 população tende para 0, 666 (aprox. )

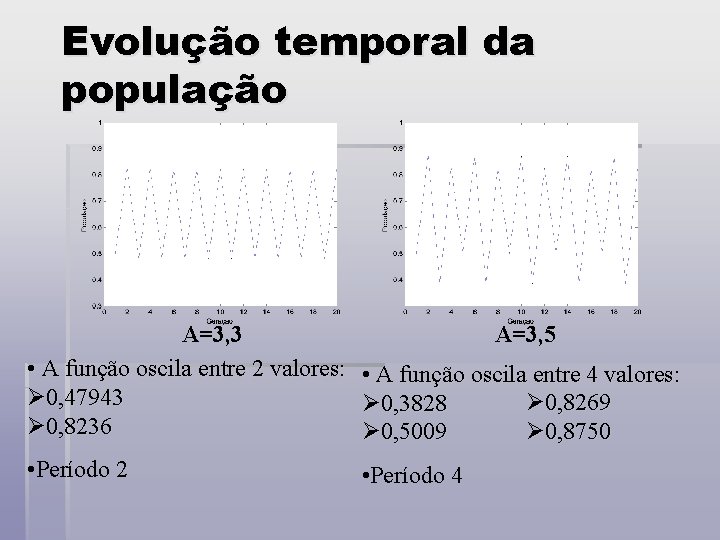
Evolução temporal da população A=3, 3 • A função oscila entre 2 valores: Ø 0, 47943 Ø 0, 8236 A=3, 5 • A função oscila entre 4 valores: Ø 0, 8269 Ø 0, 3828 Ø 0, 8750 Ø 0, 5009 • Período 2 • Período 4

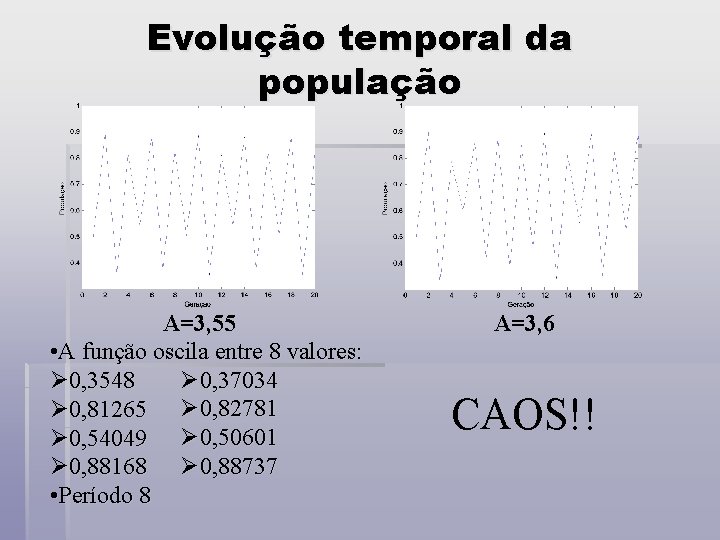
Evolução temporal da população A=3, 55 • A função oscila entre 8 valores: Ø 0, 37034 Ø 0, 3548 Ø 0, 81265 Ø 0, 82781 Ø 0, 54049 Ø 0, 50601 Ø 0, 88168 Ø 0, 88737 • Período 8 A=3, 6 CAOS!!

Caos § Não há repetição de padrões; § sequência não é aleatória ; § fenómenos caóticos são imprevisíveis; § Recorre-se ao uso do computador para evidenciar a complexidade do modelo.

4 situações: • Extinção: para valores de A<1 a população extingue-se; • Para valores de A entre 1 e 3, o sistema tende para um valor fixo; • Sistema periódico: a série alterna entre dois ou mais estados discretos consoante o valor de A escolhido; • Estado caótico.

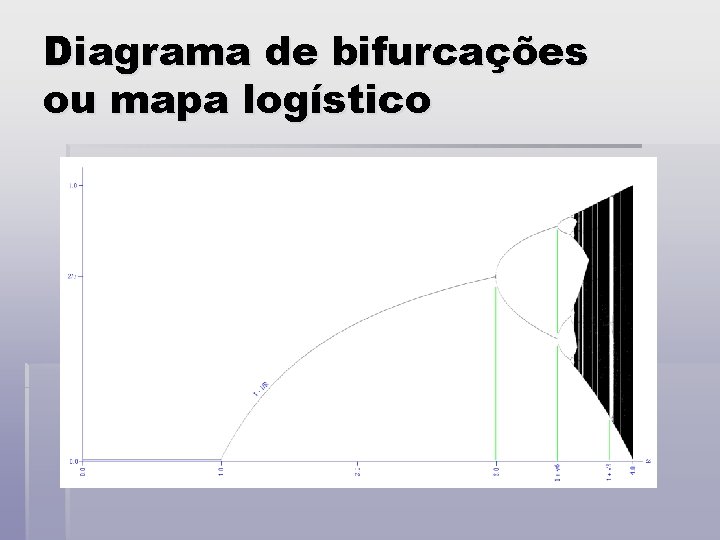
Diagrama de bifurcações ou mapa logístico

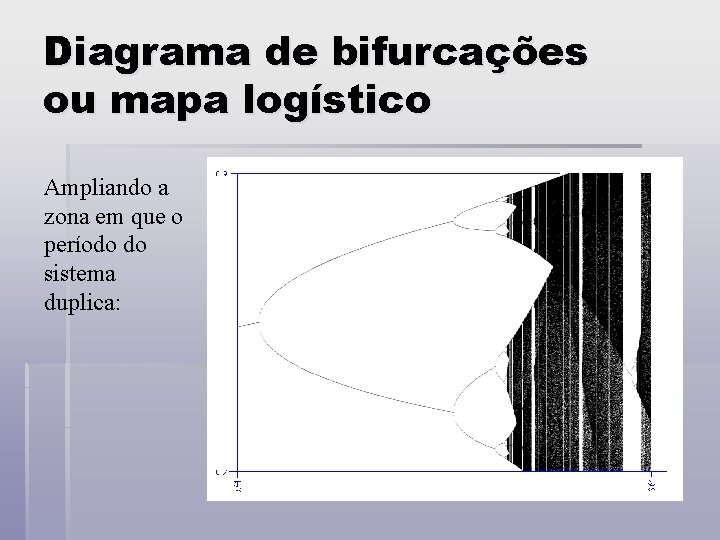
Diagrama de bifurcações ou mapa logístico Ampliando a zona em que o período do sistema duplica:

Diagrama de bifurcações ou mapa logístico § Mostra os valores que o sistema toma para diferentes valores de A; § ilustra a aproximação do caos através de uma duplicação de períodos da equação logística. § Na prática gera-se escolhendo ao acaso um valor inicial de A, e analisando de seguida os N primeiros termos da série obtida;

Constante de Feigenbaum § Obtém-se fazendo: § Nº de Feigenbaum = 4. 66920 16091 02990 67185 32038 20466 20161 72581 85577. .

Dinâmicas Populacionais com Caos SISTEMAS NÃO LINEARES Modelo de Ricker

Modelo de Ricker § Não linear § Interacções complexas que surgem no seio de uma população § população taxa de reprodução § Equação de diferenças:

Modelo de Ricker § Equação de diferenças: § § taxa de crescimento geométrico populacional quando a população é pequena: quando constante de saturação da população

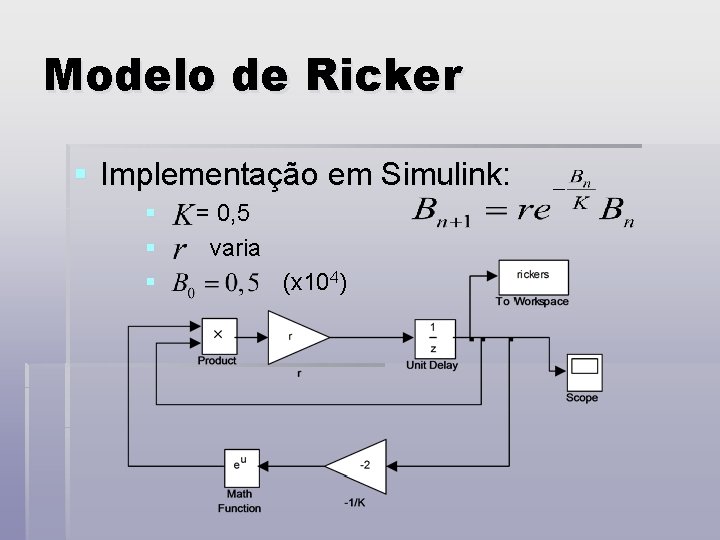
Modelo de Ricker § Implementação em Simulink: § § § = 0, 5 varia (x 104)

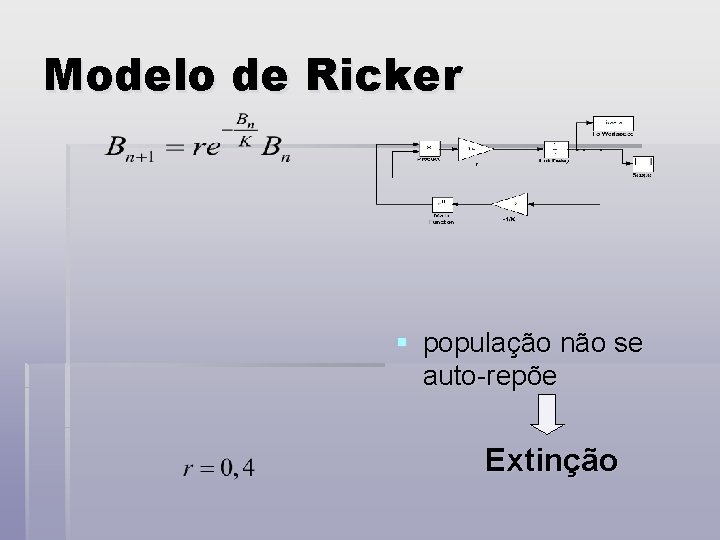
Modelo de Ricker § população não se auto-repõe Extinção

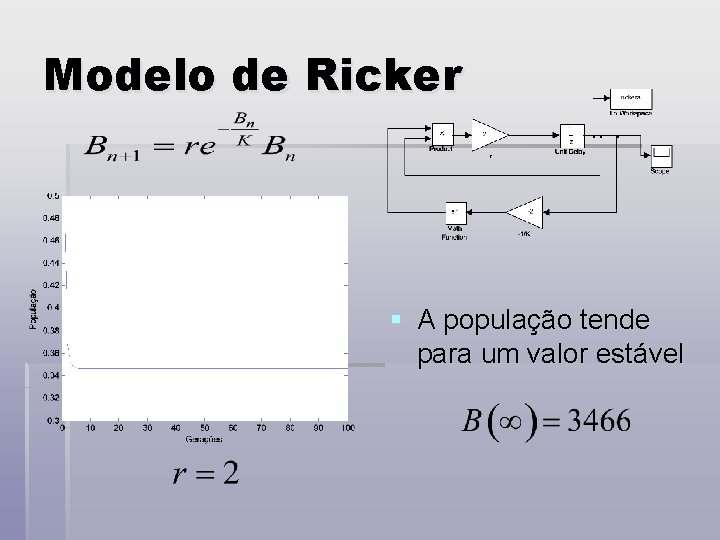
Modelo de Ricker § A população tende para um valor estável

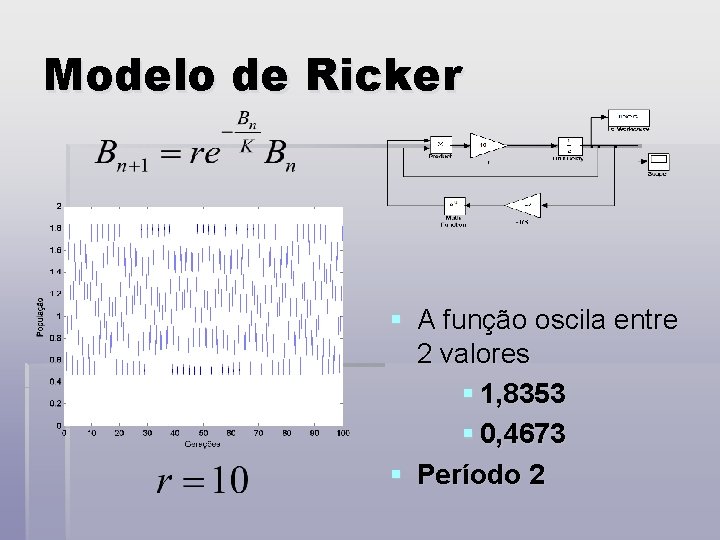
Modelo de Ricker § A função oscila entre 2 valores § 1, 8353 § 0, 4673 § Período 2

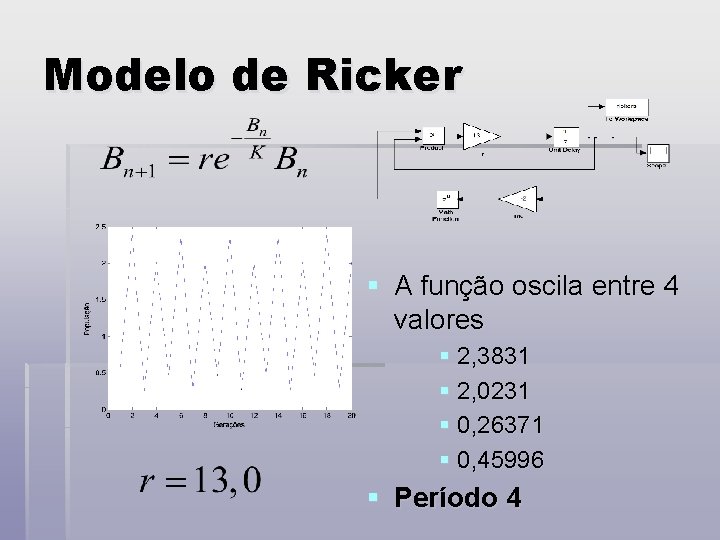
Modelo de Ricker § A função oscila entre 4 valores § 2, 3831 § 2, 0231 § 0, 26371 § 0, 45996 § Período 4

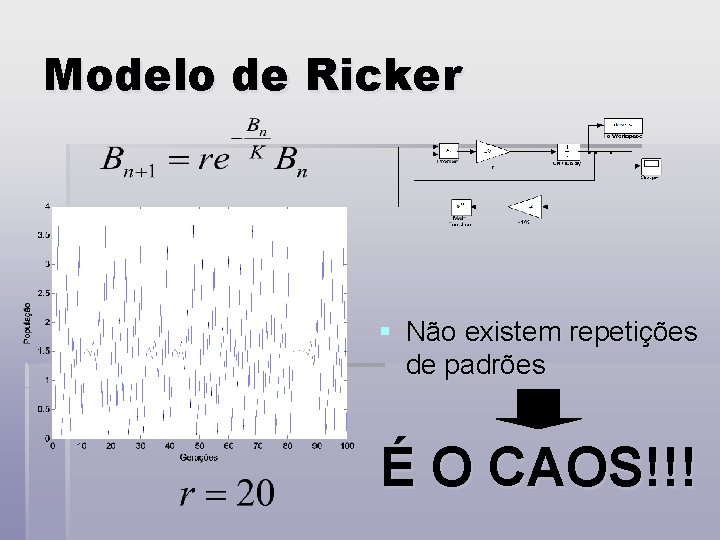
Modelo de Ricker § Não existem repetições de padrões É O CAOS!!!

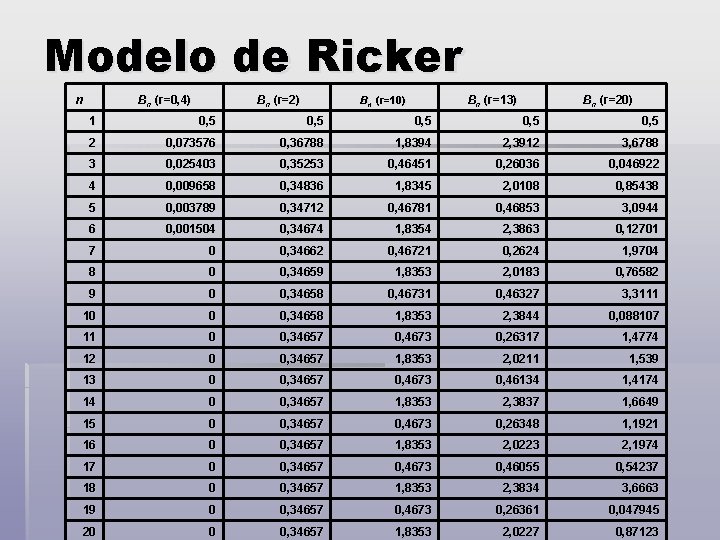
Modelo de Ricker n Bn (r=0, 4) Bn (r=2) Bn (r=13) Bn (r=10) Bn (r=20) 1 0, 5 0, 5 2 0, 073576 0, 36788 1, 8394 2, 3912 3, 6788 3 0, 025403 0, 35253 0, 46451 0, 26036 0, 046922 4 0, 009658 0, 34836 1, 8345 2, 0108 0, 85438 5 0, 003789 0, 34712 0, 46781 0, 46853 3, 0944 6 0, 001504 0, 34674 1, 8354 2, 3863 0, 12701 7 0 0, 34662 0, 46721 0, 2624 1, 9704 8 0 0, 34659 1, 8353 2, 0183 0, 76582 9 0 0, 34658 0, 46731 0, 46327 3, 3111 10 0 0, 34658 1, 8353 2, 3844 0, 088107 11 0 0, 34657 0, 4673 0, 26317 1, 4774 12 0 0, 34657 1, 8353 2, 0211 1, 539 13 0 0, 34657 0, 4673 0, 46134 1, 4174 14 0 0, 34657 1, 8353 2, 3837 1, 6649 15 0 0, 34657 0, 4673 0, 26348 1, 1921 16 0 0, 34657 1, 8353 2, 0223 2, 1974 17 0 0, 34657 0, 4673 0, 46055 0, 54237 18 0 0, 34657 1, 8353 2, 3834 3, 6663 19 0 0, 34657 0, 4673 0, 26361 0, 047945 20 0 0, 34657 1, 8353 2, 0227 0, 87123

Modelo de Ricker Comportamento estranho? Método do histograma § Determinar onde cada iteração se localiza: § Dividir o intervalo em 400 unidades iguais. § Colocar um marcador numa unidade cada vez que uma iteração a “atinge”. § No final da simulação, o número de marcadores acumulados são plotados.

Modelo de Ricker Histogramas: r=0, 4 r=10 r=20

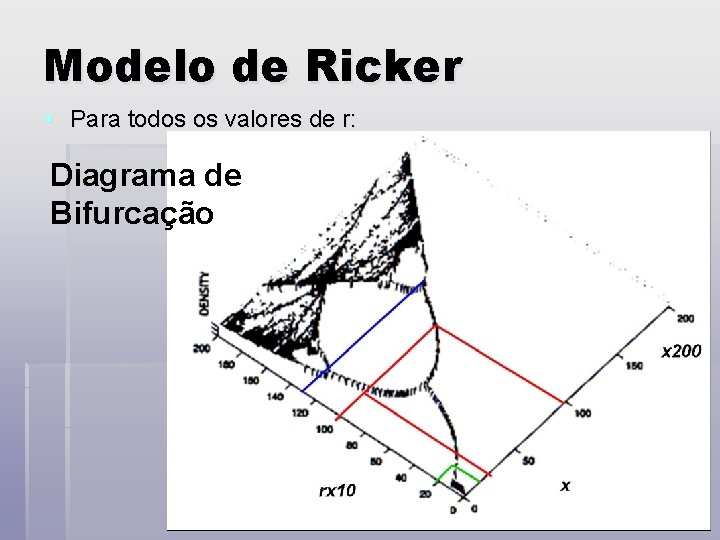
Modelo de Ricker § Para todos os valores de r: Diagrama de Bifurcação

Modelo de Ricker § Para todos os valores de r: Diagrama de Bifurcação

CAOS • Circuitos eléctricos, • Surtos epidémicos, • Batimentos cardíacos, • Actividade eléctrica cerebral, • Fluidos • Reacções químicas • Família/Comunidade • Agitação política • Bolsa • etc. …

CAOS As dinâmicas populacionais apresentam comportamentos caóticos, ocorrendo inúmeras flutuações, e os seus gráficos podem assemelhar-se a FRACTAIS.

FIM