Miskolci Egyetem Gpszmrnki s Informatikai Kar Informatikai Intzet

Miskolci Egyetem Gépészmérnöki és Informatikai Kar Informatikai Intézet Alkalmazott Informatikai Intézeti Tanszék 2016/17 2. félév 5. Előadás Dr. Kulcsár Gyula egyetemi docens

Tartalom 1. Párhuzamosan működő teljesen egyenértékű erőforrások jellemzői (P modell). 2. A feladat egzakt megoldása. 3. A P || Cmax feladat heurisztikus megoldása. 4. A P | di | Lmax feladat heurisztikus megoldása. 5. A P | pi =1; ri =integer; di =integer | Lmax feladat egzakt megoldása.

Párhuzamosan működő teljesen egyenértékű erőforrások ütemezése

A P modell jellemzői • az erőforrások teljesen egyenértékűek, • az erőforrások az ütemezési időszakban folyamatosan rendelkezésre állnak, • egy erőforrás egyszerre csak egy munkán dolgozhat, • egy munkán egyszerre csak egy erőforrás dolgozhat, • a munkák legkorábbi indítási időpontja nulla: ri = 0 (i=1, 2, …, n), • minden egyes munkához egyetlen operáció tartozik, melyeknek pontosan ismert a végrehajtási ideje: pi (i=1, 2, …, n), • az operációk végrehajtása nem szakítható meg.

A P modell jellemzői A megoldás (ütemterv) reprezentálása: • Minden erőforrásnak saját ütemezési vektora van. • A vektorok hossza megegyezik az erőforrásokhoz rendelt munkák (operációk) számával. • Minden egyes vektor tartalmazza az adott erőforráson végrehajtandó munkák indítási sorrendjét.

Párhuzamosan működő erőforrások ütemezése MSPT-szabály alkalmazásával

Az ütemezés célja • A munkák befejezési időpontjainak összege legyen minimális. Az ütemezési modell formális leírása:

Az MSPT-algoritmus

Az MSPT algoritmus Modified Shortest Processing Time, MSPT "módosított legrövidebb műveleti idejű munka előre„: • Rendezzük a munkákat az SPT szabály alkalmazásával a műveleti idő szerint nemcsökkenő sorrendbe. • Ezután képezzünk az erőforrások (gépek) számának megfelelő hosszú csoportokat. • Az első csoport munkái az elsők rendre az egyes gépeken, a második csoport munkái a másodikok rendre az egyes gépeken és így tovább.

Optimális megoldás • Az MSPT szabály a P||∑Ci feladat optimális megoldását adja. • Az állítás bizonyítása megtalálható az alábbi könyvben: Peter Brucker, Scheduling Algorithms, Springer, 2007. Megjegyzés: • Vegyük észre, hogy az adott feltételek mellett a ∑Ci célfüggvény minimalizálása egyben az átlagos átfutási időt is minimalizálja.

Illusztratív példa az MSPTalgoritmus működésére

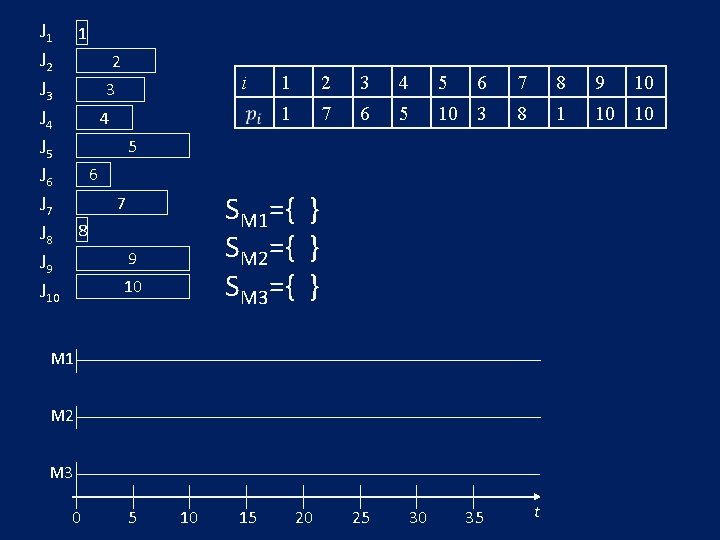
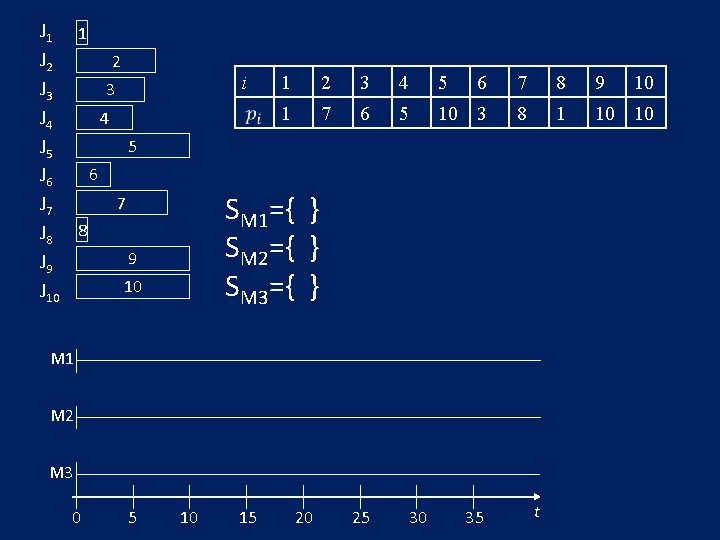
J 1 1 J 2 2 J 3 3 4 J 4 5 J 5 6 J 6 7 J 8 8 9 J 9 10 J 10 i 1 2 3 4 5 6 7 8 9 1 7 6 5 10 3 8 1 10 10 SM 1={ } SM 2={ } SM 3={ } M 1 M 2 M 3 0 5 10 15 20 25 30 35 t 10

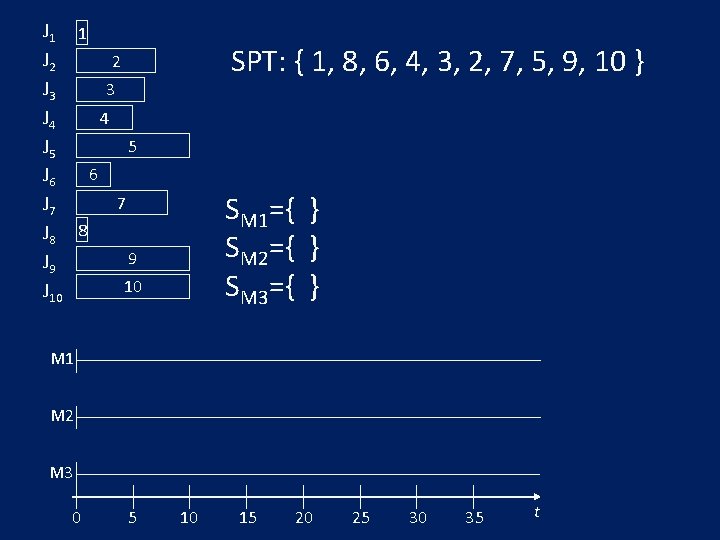
J 1 1 J 2 2 J 3 3 4 J 4 5 J 5 6 J 6 7 J 8 8 9 J 9 10 J 10 SPT: { 1, 8, 6, 4, 3, 2, 7, 5, 9, 10 } SM 1={ } SM 2={ } SM 3={ } M 1 M 2 M 3 0 5 10 15 20 25 30 35 t

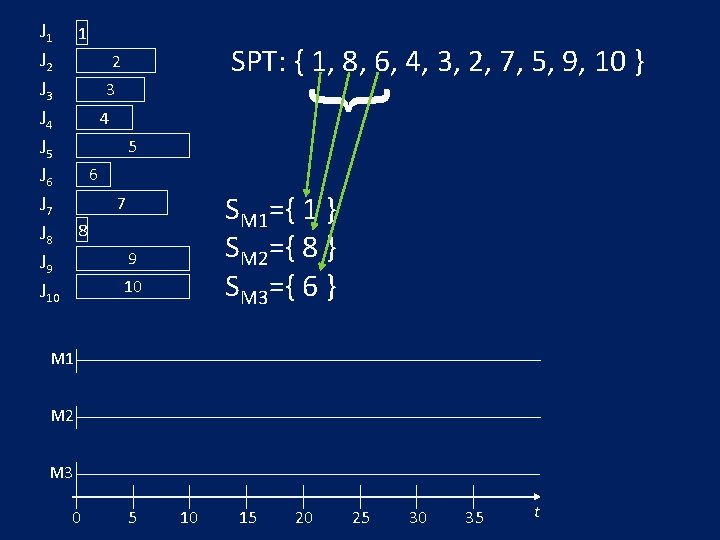
J 1 1 J 2 2 J 3 3 4 J 4 5 J 5 6 J 6 7 J 8 8 9 J 9 10 J 10 { SPT: { 1, 8, 6, 4, 3, 2, 7, 5, 9, 10 } SM 1={ 1 } SM 2={ 8 } SM 3={ 6 } M 1 M 2 M 3 0 5 10 15 20 25 30 35 t

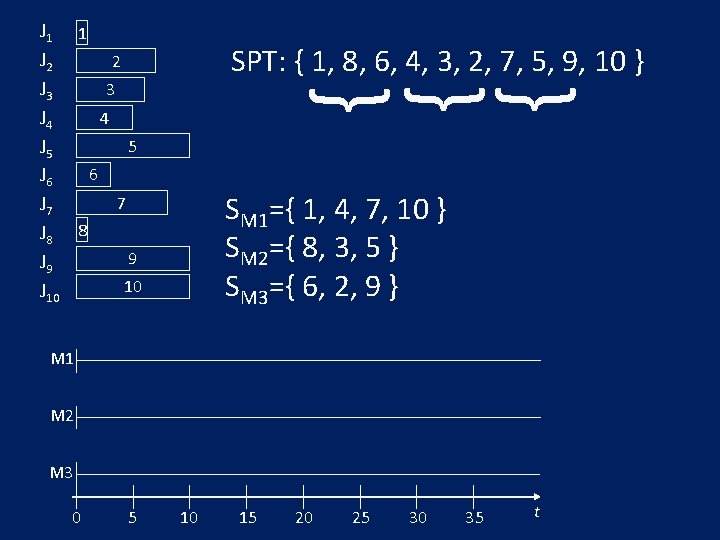
J 1 1 J 2 2 J 3 3 4 J 4 5 J 5 6 J 6 7 J 8 8 9 J 9 10 J 10 { { { SPT: { 1, 8, 6, 4, 3, 2, 7, 5, 9, 10 } SM 1={ 1, 4, 7, 10 } SM 2={ 8, 3, 5 } SM 3={ 6, 2, 9 } M 1 M 2 M 3 0 5 10 15 20 25 30 35 t

J 1 1 J 2 2 J 3 3 4 J 4 5 J 5 6 J 6 7 J 8 8 9 J 9 10 J 10 { { { SPT: { 1, 8, 6, 4, 3, 2, 7, 5, 9, 10 } SM 1={ 1, 4, 7, 10 } SM 2={ 8, 3, 5 } SM 3={ 6, 2, 9 } M 1 M 2 M 3 0 5 10 15 20 25 30 35 t

J 2 2 J 3 3 J 4 4 J 5 5 J 6 6 J 7 7 J 8 8 J 9 9 J 10 10 M 1 SM 1={ 1, 4, 7, 10 } SM 2={ 8, 3, 5 } SM 3={ 6, 2, 9 } 1 M 2 M 3 0 5 10 15 20 25 30 35 t

J 2 J 3 J 4 J 5 J 6 J 7 2 3 4 5 6 SM 1={ 1, 4, 7, 10 } SM 2={ 8, 3, 5 } SM 3={ 6, 2, 9 } 7 J 9 J 10 9 10 M 1 M 2 1 8 M 3 0 5 10 15 20 25 30 35 t

J 2 J 3 J 4 J 5 2 3 4 5 J 7 SM 1={ 1, 4, 7, 10 } SM 2={ 8, 3, 5 } SM 3={ 6, 2, 9 } 7 J 9 J 10 9 10 M 1 M 2 1 8 M 3 0 6 5 10 15 20 25 30 35 t

J 2 J 3 2 3 J 5 5 J 7 SM 1={ 1, 4, 7, 10 } SM 2={ 8, 3, 5 } SM 3={ 6, 2, 9 } 7 J 9 J 10 9 10 M 1 M 2 1 4 8 M 3 0 6 5 10 15 20 25 30 35 t

J 2 2 J 5 5 J 7 SM 1={ 1, 4, 7, 10 } SM 2={ 8, 3, 5 } SM 3={ 6, 2, 9 } 7 J 9 J 10 9 10 M 1 M 2 1 4 8 M 3 0 3 6 5 10 15 20 25 30 35 t

J 5 5 J 7 SM 1={ 1, 4, 7, 10 } SM 2={ 8, 3, 5 } SM 3={ 6, 2, 9 } 7 J 9 J 10 9 10 M 1 M 2 1 4 8 M 3 0 3 6 2 5 10 15 20 25 30 35 t

J 5 5 J 9 J 10 SM 1={ 1, 4, 7, 10 } SM 2={ 8, 3, 5 } SM 3={ 6, 2, 9 } 9 10 M 1 M 2 1 4 8 M 3 0 7 3 6 2 5 10 15 20 25 30 35 t

J 9 J 10 SM 1={ 1, 4, 7, 10 } SM 2={ 8, 3, 5 } SM 3={ 6, 2, 9 } 9 10 M 1 M 2 1 4 8 M 3 0 7 3 5 6 2 5 10 15 20 25 30 35 t

J 10 SM 1={ 1, 4, 7, 10 } SM 2={ 8, 3, 5 } SM 3={ 6, 2, 9 } 10 M 1 M 2 1 4 8 M 3 0 7 3 5 6 2 5 9 10 15 20 25 30 35 t

SM 1={ 1, 4, 7, 10 } SM 2={ 8, 3, 5 } SM 3={ 6, 2, 9 } M 1 M 2 1 4 8 M 3 0 7 3 10 5 6 2 5 9 10 15 20 25 30 35 t

Készlet-diagram A célfüggvény értéke: N 10 Az átlagos készletszint értéke: 8 6 Na ≈ 4, 29 4 2 C 1 = C 8 = 1 C 3 = 7 C 6 = 3 C 4 = 6 5 C 2 = 10 10 C 7 = 14 C 5 = 17 C 9 = 20 15 20 C 10 = 24 25 t

Párhuzamosan működő erőforrások ütemezése LPT+LIST algoritmus alkalmazásával

Az ütemezés célja • A összes munka (halmaz) teljesítésének időpontja legyen minimális (az utolsóként elkészülő munka befejezési időpontja a lehető legkorábbi legyen). Cmax = max{C 1, … , CN} Cmax min Az ütemezési modell formális leírása:

Az LPT+LIST algoritmus

Az LPT+LIST algoritmus: • 1. fázis: Előkészítés LPT algoritmussal. Rendezzük a munkákat a műveleti idő szerint nemnövekvő sorrendbe (Longest Processing Time, LPT). Ennek az a célja, hogy először a nagyobb terhelést jelentő munkákat helyezzük el az ütemtervben, majd aztán a kisebbeket. Ennek az előnye az, hogy a menet közben viszonylag jól kiegyenlített terhelések végére ne kellejen egy nagy "kilógó" munkát beilleszteni. • 2. fázis: Ütemezés LIST algoritmussal. Az LPT szerint rendezett munkákat egyesével tesszük be az ütemtervbe úgy, hogy mindig a lista elejéről a még be nem ütemezettek közül a legnagyobb műveleti idejű munkáról hozunk döntést. A soron következő munkát ahhoz a géphez rendeljük hozzá, amelyik a legkorábban felszabadul a terhelései alól. A beütemezendő munkát mindig a kiválasztott gép ütemezési vektorának a végére helyezzük el.

Heurisztikus megoldás • A P||Cmax ütemezési feladat általános esetben nem oldható meg egzakt módon polinomiális futási idejű algoritmussal. Ezért heurisztikus megoldási módszert használunk, amely gyorsan előállít egy jó közelítő megoldást, de az optimális megoldást nem tudja garantálni. Az LPT+LIST heurisztikus módszer alapja: • A munkák minél egyenletesebb szétosztása.

Megjegyzések 1. Az LPT+LIST algoritmus felépítő jellegű: az ütemterv kidolgozása közben hozott döntést a későbbi döntések nem változtatják meg. – Ha egy munkát hozzárendeltünk egy géphez, és beállítottuk a végrehajtási sorban a pozícióját, akkor a későbbi dontések ezt már nem változtatják meg, mert mindig a lista végére illesztjük a soron következő munkát. 2. A feladat megoldására kereső algoritmusokat is alkalmazhatunk. (Lásd a később!)

Illusztratív példa az LPT+LIST algoritmus működésére

J 1 1 J 2 2 J 3 3 4 J 4 5 J 5 6 J 6 7 J 8 8 9 J 9 10 J 10 i 1 2 3 4 5 6 7 8 9 1 7 6 5 10 3 8 1 10 10 SM 1={ } SM 2={ } SM 3={ } M 1 M 2 M 3 0 5 10 15 20 25 30 35 t 10

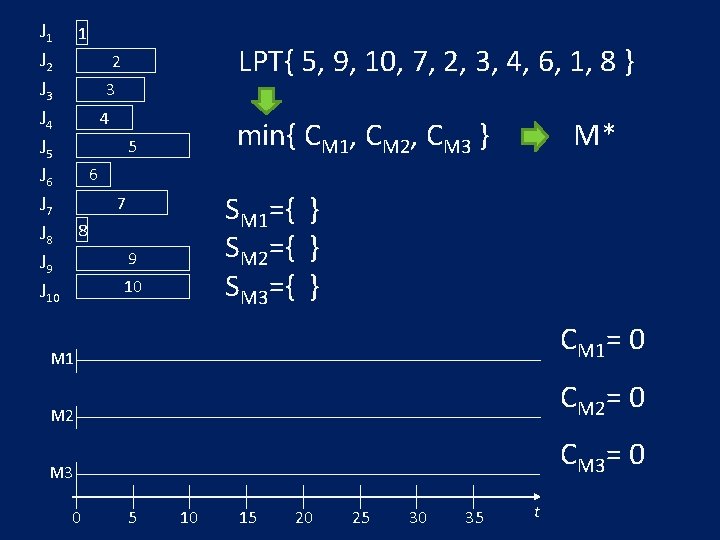
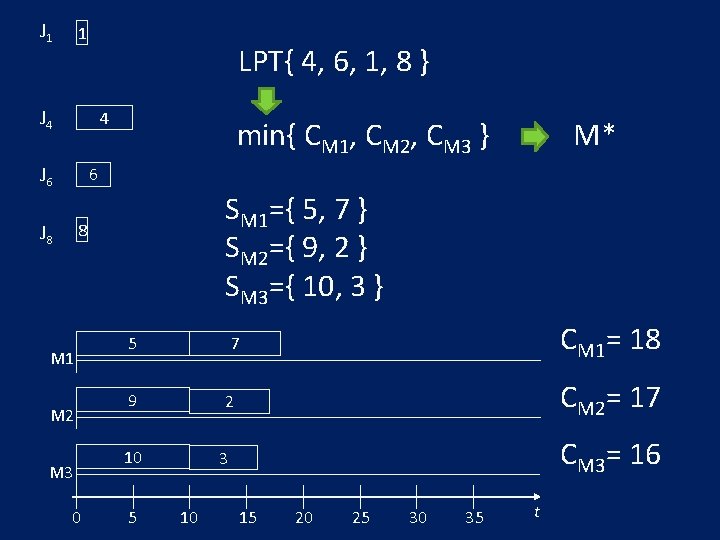
J 1 1 J 2 2 J 3 3 4 J 4 5 J 5 6 J 6 7 J 8 8 9 J 9 10 J 10 LPT{ 5, 9, 10, 7, 2, 3, 4, 6, 1, 8 } min{ CM 1, CM 2, CM 3 } M* SM 1={ } SM 2={ } SM 3={ } M 1 CM 1= 0 M 2 CM 2= 0 M 3 CM 3= 0 0 5 10 15 20 25 30 35 t

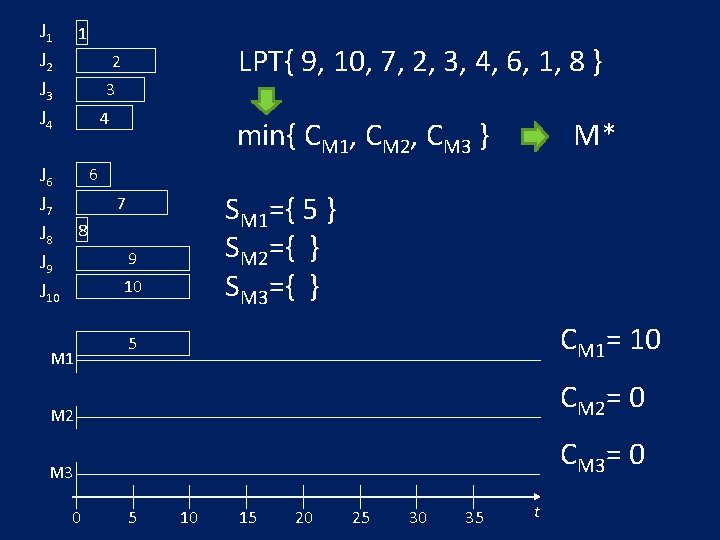
J 1 J 2 J 3 J 4 1 LPT{ 9, 10, 7, 2, 3, 4, 6, 1, 8 } 2 3 4 min{ CM 1, CM 2, CM 3 } 6 J 6 7 J 8 8 9 J 9 10 J 10 M 1 M* SM 1={ 5 } SM 2={ } SM 3={ } CM 1= 10 5 M 2 CM 2= 0 M 3 CM 3= 0 0 5 10 15 20 25 30 35 t

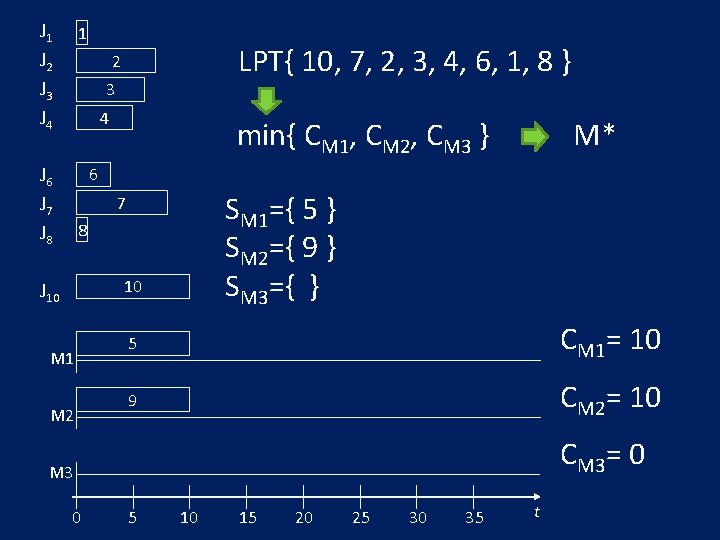
J 1 J 2 J 3 J 4 1 LPT{ 10, 7, 2, 3, 4, 6, 1, 8 } 2 3 4 J 6 J 7 J 8 min{ CM 1, CM 2, CM 3 } M* 6 SM 1={ 5 } SM 2={ 9 } SM 3={ } 7 8 10 J 10 M 1 M 2 5 CM 1= 10 9 CM 2= 10 CM 3= 0 M 3 0 5 10 15 20 25 30 35 t

J 1 J 2 J 3 J 4 1 LPT{ 7, 2, 3, 4, 6, 1, 8 } 2 3 4 J 6 J 7 J 8 min{ CM 1, CM 2, CM 3 } M* 6 SM 1={ 5 } SM 2={ 9 } SM 3={ 10 } 7 8 M 1 M 2 M 3 0 5 CM 1= 10 9 CM 2= 10 10 CM 3= 10 5 10 15 20 25 30 35 t

J 1 J 2 J 3 J 4 1 LPT{ 2, 3, 4, 6, 1, 8 } 2 3 4 J 6 min{ CM 1, CM 2, CM 3 } M* 6 SM 1={ 5, 7 } SM 2={ 9 } SM 3={ 10 } 8 J 8 M 1 M 2 M 3 0 5 CM 1= 18 7 9 CM 2= 10 10 CM 3= 10 5 10 15 20 25 30 35 t

J 1 1 J 3 J 4 LPT{ 3, 4, 6, 1, 8 } 3 4 J 6 min{ CM 1, CM 2, CM 3 } M* 6 SM 1={ 5, 7 } SM 2={ 9, 2 } SM 3={ 10 } 8 J 8 M 1 M 2 M 3 0 5 CM 1= 18 7 9 CM 2= 17 2 CM 3= 10 10 5 10 15 20 25 30 35 t

J 1 1 LPT{ 4, 6, 1, 8 } J 4 4 J 6 min{ CM 1, CM 2, CM 3 } M* 6 SM 1={ 5, 7 } SM 2={ 9, 2 } SM 3={ 10, 3 } 8 J 8 M 1 M 2 M 3 0 5 9 CM 2= 17 2 10 5 CM 1= 18 7 CM 3= 16 3 10 15 20 25 30 35 t

J 1 1 LPT{ 6, 1, 8 } min{ CM 1, CM 2, CM 3 } J 6 M* 6 SM 1={ 5, 7 } SM 2={ 9, 2 } SM 3={ 10, 3, 4 } 8 J 8 M 1 M 2 M 3 0 5 9 CM 2= 17 2 10 5 CM 1= 18 7 3 10 CM 3= 21 4 15 20 25 30 35 t

J 1 1 LPT{ 1, 8 } min{ CM 1, CM 2, CM 3 } SM 1={ 5, 7 } SM 2={ 9, 2, 6 } SM 3={ 10, 3, 4 } 8 J 8 M 1 M 2 M 3 0 M* 5 9 2 10 5 CM 1= 18 7 3 10 15 6 CM 2= 20 4 CM 3= 21 20 25 30 35 t

LPT{ 8 } min{ CM 1, CM 2, CM 3 } SM 1={ 5, 7, 1 } SM 2={ 9, 2, 6 } SM 3={ 10, 3, 4 } 8 J 8 M 1 M 2 M 3 0 M* 5 7 9 2 10 5 3 10 15 1 CM 1= 19 6 CM 2= 20 4 CM 3= 21 20 25 30 35 t

LPT{ } min{ CM 1, CM 2, CM 3 } M* SM 1={ 5, 7, 1, 8 } SM 2={ 9, 2, 6 } SM 3={ 10, 3, 4 } M 1 M 2 M 3 0 5 7 9 2 10 5 3 10 15 18 CM 1= 20 6 CM 2= 20 4 CM 3= 21 20 25 30 35 t

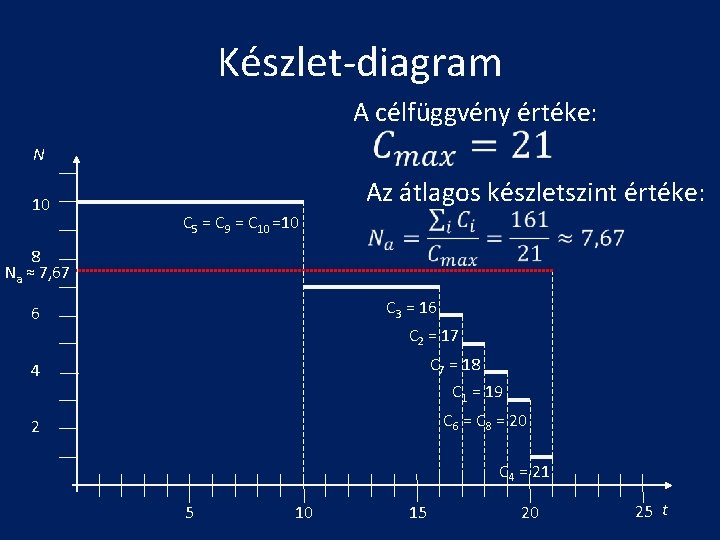
Készlet-diagram A célfüggvény értéke: N 10 Az átlagos készletszint értéke: C 5 = C 9 = C 10 =10 8 Na ≈ 7, 67 C 3 = 16 6 C 2 = 17 C 7 = 18 4 C 1 = 19 C 6 = C 8 = 20 2 C 4 = 21 5 10 15 20 25 t

Párhuzamosan működő erőforrások ütemezése EDD+LIST algoritmus alkalmazásával

Az ütemezés célja • A legnagyobb késés minimalizálása L i = Ci - d i Lmax = max{L 1, …, Li , …, LN} = maxi { Li } Lmax min Az ütemezési modell formális leírása:

Az EDD+LIST algoritmus

Az EDD+LIST algoritmus: • 1. fázis: Előkészítés EDD algoritmussal. Rendezzük a munkákat a határidők szerint nemcsökkenő sorrendbe (Earliest Due Date, EDD). Ennek az a célja, hogy először a korábbi határidejű munkákat helyezzük el az ütemtervben, majd aztán a későbbi határidejűeket. 2. fázis: Ütemezés LIST algoritmussal. Az EDD szerint rendezett munkákat egyesével tesszük be az ütemtervbe úgy, hogy mindig a lista elejéről a még be nem ütemezettek közül a legkorábbi határidejű munkáról hozunk döntést. A soron következő munkát ahhoz a géphez rendeljük hozzá, amelyik a legkorábban felszabadul a terhelései alól. A beütemezendő munkát mindig a kiválasztott gép ütemezési vektorának a végére helyezzük el.

Heurisztikus megoldás • A P|di |Lmax ütemezési feladat általános esetben nem oldható meg egzakt módon polinomiális futási idejű algoritmussal. Ezért heurisztikus megoldási módszert használunk, amely gyorsan előállít egy jó közelítő megoldást, de az optimális megoldást nem tudja garantálni. Az EDD+LIST heurisztikus módszer alapja: • Az 1|di |Lmax és a P||Cmax feladat megoldási módszerének kombinálása.

Megjegyzések 1. Az EDD+LIST algoritmus felépítő jellegű: az LPT+LIST algoritmushoz hasonlóan. 2. A feladat megoldására kereső algoritmusokat is alkalmazhatunk. (Lásd később!)

Párhuzamosan működő erőforrások ütemezése tartalékidő-orientált algoritmus alkalmazásával

Erőforrás-korlátos ütemezési modell A feladat jellemzői: • N számú egymástól független munka: Ji (i=1, 2, …, n) • – legkorábbi indítási időpont (ri) – legkésőbbi befejezési időpont (di) szerelő szakmunkások (erőforrások) – erőforrás-rendelkezésre állást definiáló lista: kezdési időpontok szerint növekvő sorrendbe rendezett, átlapolódás nélküli fix hosszúságú időintervallumszakaszok – az időintervallumokban külön-külön előírt számú munka végezhető el • cél: a határidő túllépés maximális értéke a lehető legkisebb legyen (Lmax min)

Probléma-transzformáció Továbbfejlesztett párhuzamos gépes ütemezési feladat 1. Az erőforrások rendelkezésre-állási időintervallumait folyamatosan, decimális egészekkel sorszámozzuk lépések (s). 2. A műveleti idők egységnyi értéket (lépést) vesznek fel (pi = 1). 3. A munkák időadatait átalakítjuk lépésekre: – ri a befogadó műszakot követő műszak lépésszáma – di a befogadó műszak sorszáma – A teljesítés időpontját (Ci) a befogadó műszak sorszámával kifejezett alakban keressük.

Probléma-transzformáció (folyt. ) 4. (Li = Ci - di) a munka késését is egységnyi lépésben mérjük. 5. Szerelő szakmunkások párhuzamosan működő virtuális erőforrások – egy erőforrás egyszerre csak egy munkán dolgozhat – egy munkán egyszerre csak egy erőforrás dolgozhat – a virtuális erőforrások száma lépésenként eltérő lehet: P(s) A transzformált feladat: P(s) | pi=1; ri=egész; di=egész | Lmax

Időtartalék-orientált algoritmus a P(s) | pi=1; ri=integer; di=integer | Lmax feladathoz { Rendezzük a Ji (i=1, 2, …, NJ) munkákat ri szerint nem csökkenő sorrendbe; item ← 1; while (item ≤ N) { s ← ritem; while (P(s) < 1) { s ← s + 1; if (s > smax) Kilépés megvalósítható megoldás nélkül; } R ← {Ji | Ji nem ütemezett és ri ≤ s}; mach ← 1; while (R nem üres) { Válasszuk ki a legkisebb di határidővel rendelkező Ji munkát az R-ből; R ← R {Ji}; Ütemezzük a Ji-t a mach. -edik gépre az s műszakban; Ci ← s; Li ← Ci - di; Ti ← max(0, Li); item ← item + 1; //folytatás a következő lapon

//folytatás if (mach + 1 ≤ P(s)) mach ← mach + 1; else { mach ← 1; s ← s + 1; while (P(s) < 1) { s ← s + 1; if (s > smax) Kilépés megvalósítható megoldás nélkül; } R ← R ∪ {Ji | Ji nem ütemezett és ri ≤ s} } Visszatérés az elkészített optimális megoldással; }

Eredmények • Az algoritmus a Ci értékek kiszámításával egyben elő is állítja a keresett megoldást: – A Ji munkát az s = Ci sorszámú műszakban kell elvégezni. • Minimális késés: Lmax min. • Polinomiális futási idő.

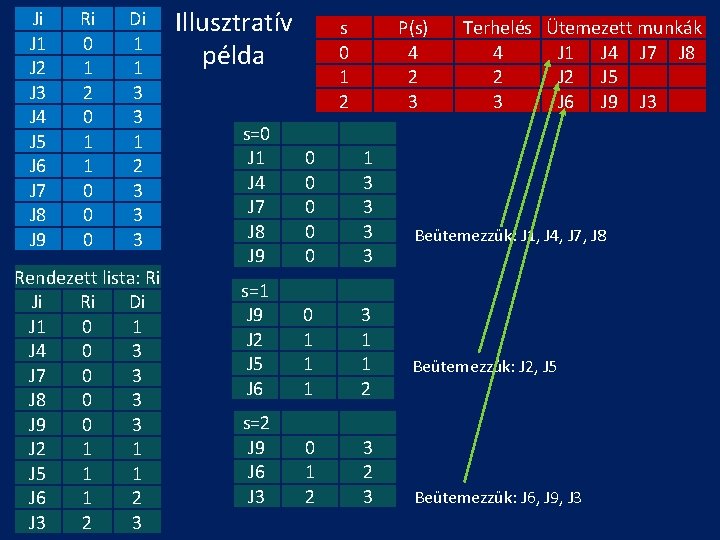
Ji J 1 J 2 J 3 J 4 J 5 J 6 J 7 J 8 J 9 Ri 0 1 2 0 1 1 0 0 0 Di 1 1 3 3 1 2 3 3 3 Rendezett lista: Ri Ji Ri Di J 1 0 1 J 4 0 3 J 7 0 3 J 8 0 3 J 9 0 3 J 2 1 1 J 5 1 1 J 6 1 2 J 3 2 3 Illusztratív példa s 0 1 2 P(s) 4 2 3 s=0 J 1 J 4 J 7 J 8 J 9 0 0 0 1 3 3 s=1 J 9 J 2 J 5 J 6 0 1 1 1 3 1 1 2 s=2 J 9 J 6 J 3 0 1 2 3 Terhelés Ütemezett munkák 4 J 1 J 4 J 7 J 8 2 J 5 3 J 6 J 9 J 3 Beütemezzük: J 1, J 4, J 7, J 8 Beütemezzük: J 2, J 5 Beütemezzük: J 6, J 9, J 3

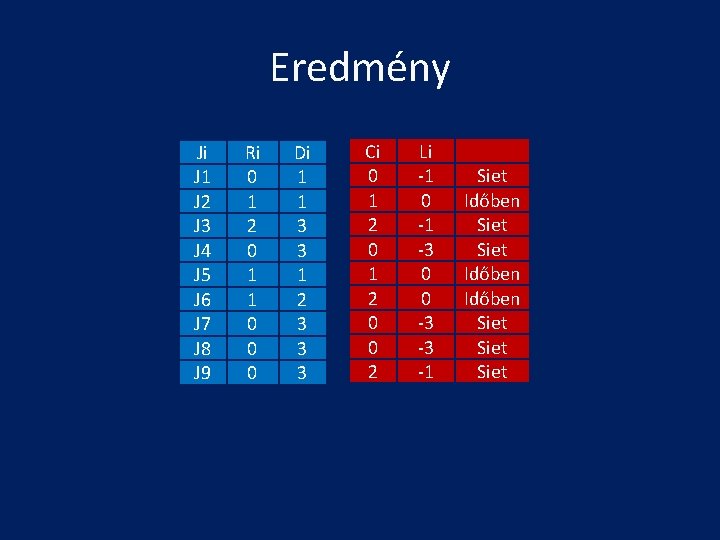
Eredmény Ji J 1 J 2 J 3 J 4 J 5 J 6 J 7 J 8 J 9 Ri 0 1 2 0 1 1 0 0 0 Di 1 1 3 3 1 2 3 3 3 Ci 0 1 2 0 0 2 Li -1 0 -1 -3 0 0 -3 -3 -1 Siet Időben Siet

Köszönöm a figyelmet! Az előadásvázlat elérhető az alábbi webcímen: http: //ait. iit. uni-miskolc. hu/~kulcsar/serv 07. htm