Maxwells Equations in Vacuum 1 E r o






















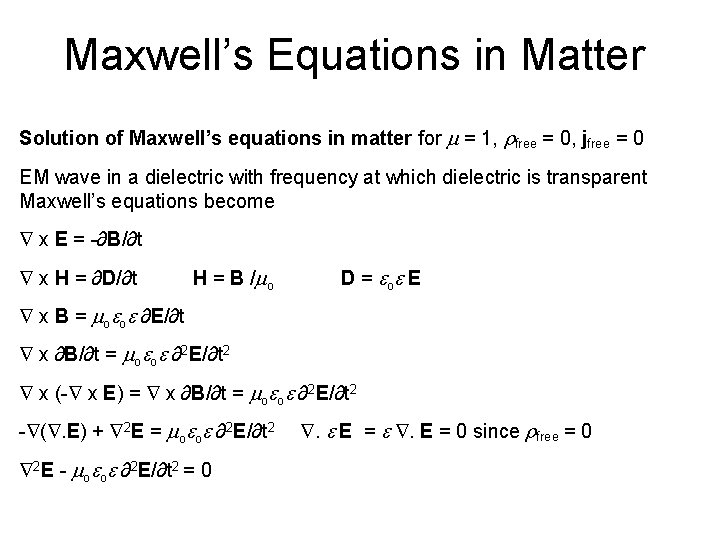
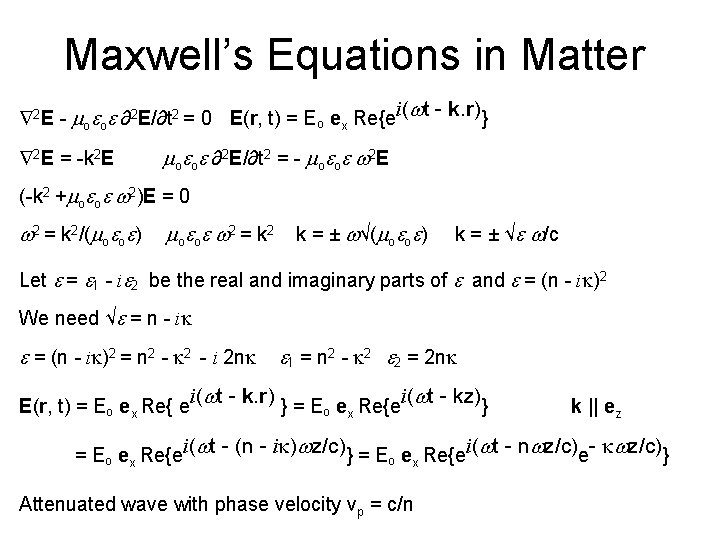
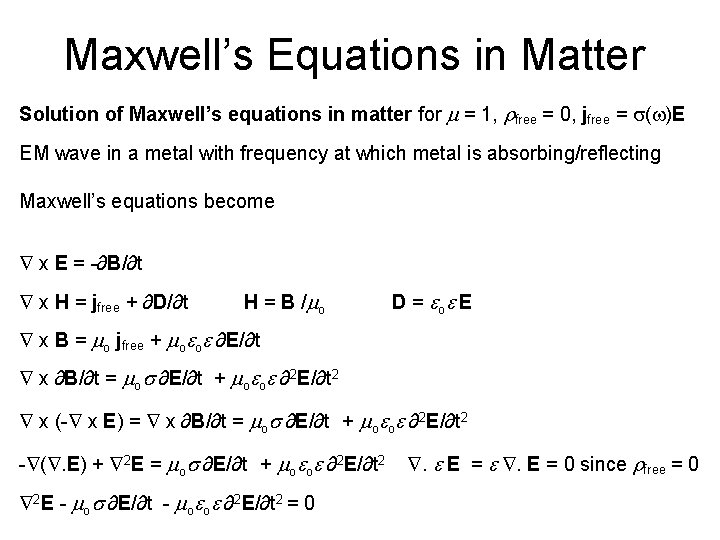









- Slides: 37

Maxwell’s Equations in Vacuum (1) . E = r / o Poisson’s Equation (2) . B = 0 No magnetic monopoles (3) x E = -∂B/∂t Faraday’s Law (4) x B = moj + mo o∂E/∂t Maxwell’s Displacement Electric Field E Vm-1 Magnetic Induction B Tesla Charge density r Cm-3 Current Density Cm-2 s-1 Ohmic Conduction j = s E Electric Conductivity Siemens (Mho)

Constitutive Relations (1) D = o. E + P Electric Displacement D Cm-2 and Polarization P Cm-2 (2) P = o c E Electric Susceptibility c (3) =1+ c Relative Permittivity (dielectric function) (4) D = o E (5) H = B / mo – M (6) M = c. B B / mo (7) m =1 / (1 - c. B) (8) H = B / m mo Magnetic Field H Am-1 and Magnetization M Am-1 Magnetic Susceptibility c. B Relative Permeability m m ~ 1 (non-magnetic materials), ~ 1 - 50

Electric Polarisation • Apply Gauss’ Law to right and left ends of polarised dielectric s- s+ P E- E+ • EDep = ‘Depolarising field’ • Macroscopic electric field E s± surface charge density Cm-2 s± = P. n n outward normal E+2 d. A = s+d. A/ o Gauss’ Law E+ = s+/2 o E- = s-/2 o EDep = E+ + E- = (s++ s-)/2 o EDep = -P/ o P = s+ = s- EMac= E + EDep = E - P/ o

Electric Polarisation Define dimensionless dielectric susceptibility c through P = o c EMac = E – P/ o o E = o EMac + P o E = o EMac + o c EMac = o (1 + c)EMac = o EMac Define dielectric constant (relative permittivity) = 1 + c EMac = E / E = EMac Typical values for : silicon 11. 8, diamond 5. 6, vacuum 1 Metal: →∞ Insulator: ∞ (electronic part) small, ~5, lattice part up to 20

Electric Polarisation Rewrite EMac = E – P/ o as o. EMac + P = o. E LHS contains only fields inside matter, RHS fields outside Displacement field, D D = o. EMac + P = o EMac = o. E Displacement field defined in terms of EMac (inside matter, relative permittivity ) and E (in vacuum, relative permittivity 1). Define D = o E where is the relative permittivity and E is the electric field

Gauss’ Law in Matter • Uniform polarisation → induced surface charges only - P E + • Non-uniform polarisation → induced bulk charges also + - Displacements of positive charges Accumulated charges

Gauss’ Law in Matter Polarisation charge density Charge entering xz face at y = 0: Py=0 Dx. Dz Cm-2 m 2 = C Charge leaving xz face at y = Dy: Py=Dy. Dx. Dz = (Py=0 + ∂Py/∂y Dy) Dx. Dz Net charge entering cube via xz faces: (Py=0 - Py=Dy ) Dx. Dz = -∂Py/∂y Dx. Dy. Dz z Py=0 -(∂Px/∂x + ∂Py/∂y + ∂Pz/∂z) Dx. Dy. Dz = Qpol Dz Dy Dx x Charge entering cube via all faces: Py=Dy y rpol = lim (Dx. Dy. Dz)→ 0 Qpol /(Dx. Dy. Dz) -. P = rpol

Gauss’ Law in Matter Differentiate -. P = rpol wrt time . ∂P/∂t + ∂rpol/∂t = 0 Compare to continuity equation . j + ∂r/∂t = 0 ∂P/∂t = jpol Rate of change of polarisation is the polarisation-current density Suppose that charges in matter can be divided into ‘bound’ or polarisation and ‘free’ or conduction charges rtot = rpol + rfree

Gauss’ Law in Matter Inside matter . E = . Emac = rtot/ o = (rpol + rfree)/ o Total (averaged) electric field is the macroscopic field -. P = rpol . ( o. E + P) = rfree . D = rfree Introduction of the displacement field, D, allows us to eliminate polarisation charges from any calculation. This is a form of Gauss’ Law suitable for application in matter.

Ampère’s Law in Matter Ampère’s Law Problem! Continuity equation A steady current implies constant charge density, so Ampère’s law is consistent with the continuity equation for steady currents Ampère’s law is inconsistent with the continuity equation (conservation of charge) when the charge density is time dependent

Ampère’s Law in Matter Add term to LHS such that taking Div makes LHS also identically equal to zero: The extra term is in the bracket extended Ampère’s Law Displacement current (vacuum)

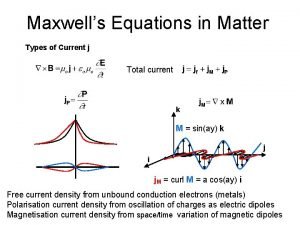
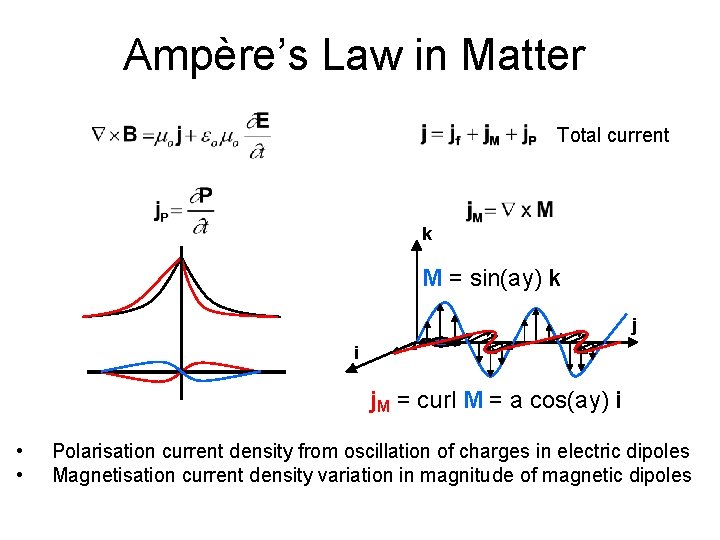
Ampère’s Law in Matter Total current k M = sin(ay) k j i j. M = curl M = a cos(ay) i • • Polarisation current density from oscillation of charges in electric dipoles Magnetisation current density variation in magnitude of magnetic dipoles

Ampère’s Law in Matter ∂D/∂t is the displacement current postulated by Maxwell (1862) In vacuum D = o. E ∂D/∂t = o ∂E/∂t In matter D = o E ∂D/∂t = o ∂E/∂t Displacement current exists throughout space in a changing electric field

Maxwell’s Equations in vacuum in matter . E = r / o . D = rfree Poisson’s Equation . B = 0 No magnetic monopoles x E = -∂B/∂t Faraday’s Law x B = moj + mo o∂E/∂t x H = jfree + ∂D/∂t Maxwell’s Displacement D = o E = o(1+ c)E Constitutive relation for D H = B/(mom) = (1 - c. B)B/mo Constitutive relation for H

Divergence Theorem 2 -D 3 -D • From Green’s Theorem • In words - Integral of A. n d. A over surface contour equals integral of div A over surface area A. n d. A d. V • In 3 -D • Integral of A. n d. A over bounding surface S equals integral of div V d. V within volume enclosed by surface S • The area element n d. A is conveniently written as d. S

Differential form of Gauss’ Law • Integral form • Divergence theorem applied to field V, volume v bounded by surface S V. d. S . V dv • Divergence theorem applied to electric field E Differential form of Gauss’ Law (Poisson’s Equation)

Stokes’ Theorem 3 -D • In words - Integral of ( x A). n d. A over surface S equals integral of A. dr over bounding contour C • It doesn’t matter which surface (blue or hatched). Direction of dr determined by right hand rule. local value of x A n outward normal A dr C d. A ( x a). nd. A A. dr local value of A

Faraday’s Law

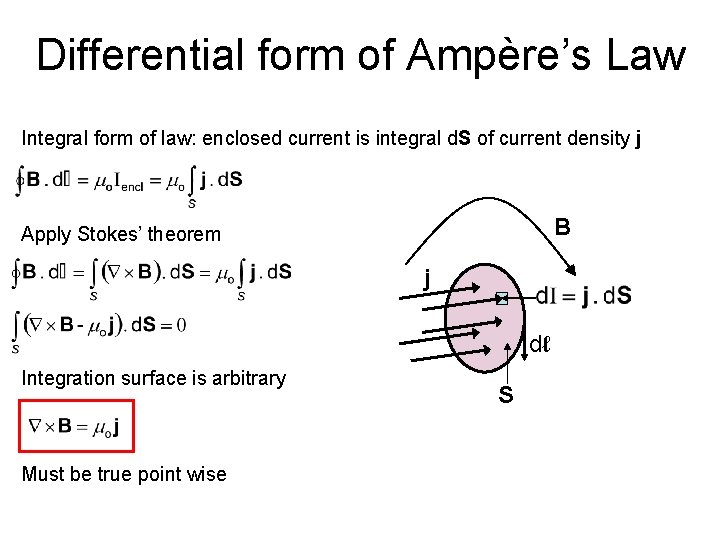
Differential form of Ampère’s Law Integral form of law: enclosed current is integral d. S of current density j B Apply Stokes’ theorem j dℓ Integration surface is arbitrary Must be true point wise S

Maxwell’s Equations in Vacuum Take curl of Faraday’s Law (3) x ( x E) = -∂ ( x B)/∂t = -∂ (mo o∂E/∂t)/∂t = -mo o∂2 E/∂t 2 x ( x E) = (. E) - 2 E vector identity (. E = 0) - 2 E = -mo o∂2 E/∂t 2 2 E -mo o∂2 E/∂t 2 = 0 Vector wave equation

Maxwell’s Equations in Vacuum Plane wave solution to wave equation E(r, t) = Re {Eo ei(wt - k. r)} Eo constant vector 2 E =(∂2/∂x 2 + ∂2/∂y 2 + ∂2/∂z 2)E = -k 2 E . E = ∂Ex/∂x + ∂Ey/∂y + ∂Ez/∂z = -ik. Eo ei(wt - k. r) If Eo || k then . E ≠ 0 and x E = 0 If Eo ┴ k then . E = 0 and x E ≠ 0 For light Eo ┴ k and E(r, t) is a transverse wave

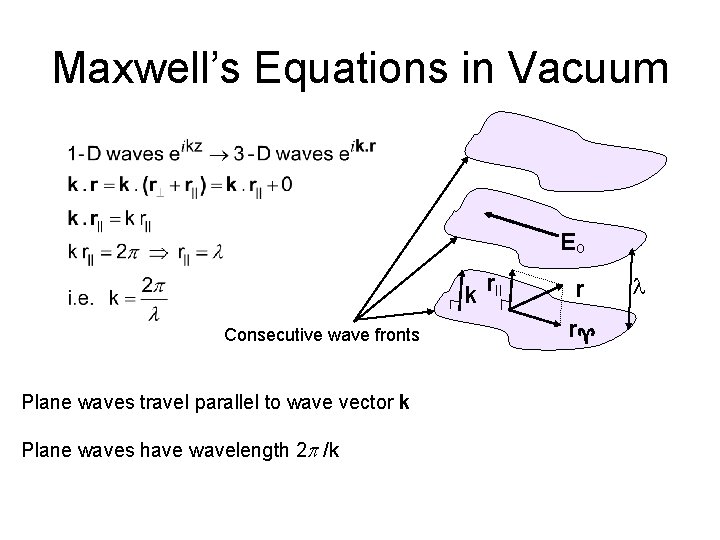
Maxwell’s Equations in Vacuum Eo k r|| Consecutive wave fronts Plane waves travel parallel to wave vector k Plane waves have wavelength 2 p /k r r l

Maxwell’s Equations in Vacuum Plane wave solution to wave equation E(r, t) = Eo ei(wt - k. r) Eo constant vector mo o∂2 E/∂t 2 = - mo ow 2 E mo ow 2 = k 2 w =±k/(mo o)1/2 = ±ck w/k = c = (mo o)-1/2 phase velocity w(k) w = ±ck Linear dispersion relationship k

Maxwell’s Equations in Vacuum Magnetic component of the electromagnetic wave in vacuum From Maxwell-Ampère and Faraday laws x ( x B) = mo o ∂( x E)/∂t = mo o ∂(-∂B/∂t)/∂t = -mo o∂2 B/∂t 2 x ( x B) = (. B) - 2 B = -mo o∂2 B/∂t 2 (. B = 0) 2 B -mo o∂2 B/∂t 2 = 0 Same vector wave equation as for E

Maxwell’s Equations in Vacuum If E(r, t) = Eo ex ei(wt - k. r) and k || ez and E || ex (ex, ey, ez unit vectors) x E = -ik Eo ey ei(wt - k. r) = -∂B/∂t From Faraday’s Law ∂B/∂t = ik Eo ey ei(wt - k. r) B = (k/w) Eo ey ei(wt - k. r) = (1/c) Eo ey ei(wt - k. r) For this wave E || ex, B || ey, k || ez, c. Bo = Eo More generally -∂B/∂t = -iw B = x E = -i k x E -iw B = -i k x E B = ek x E / c ex ez ey
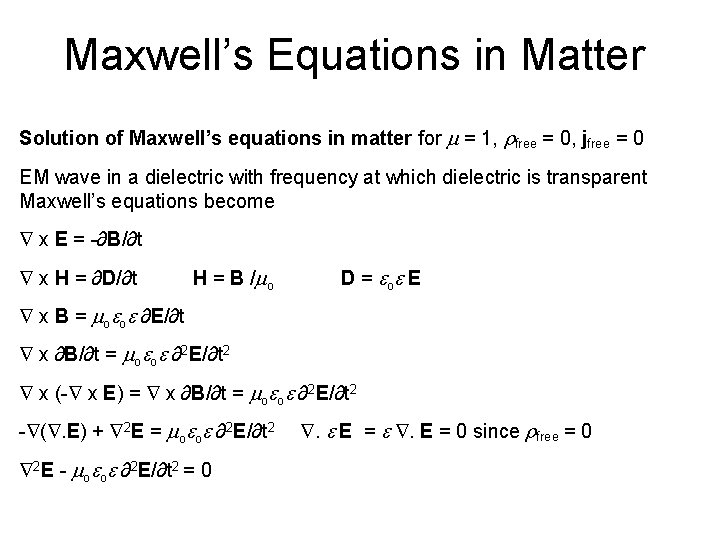
Maxwell’s Equations in Matter Solution of Maxwell’s equations in matter for m = 1, rfree = 0, jfree = 0 EM wave in a dielectric with frequency at which dielectric is transparent Maxwell’s equations become x E = -∂B/∂t x H = ∂D/∂t H = B /mo D = o E x B = mo o ∂E/∂t x ∂B/∂t = mo o ∂2 E/∂t 2 x (- x E) = x ∂B/∂t = mo o ∂2 E/∂t 2 - (. E) + 2 E = mo o ∂2 E/∂t 2 . E = . E = 0 since rfree = 0 2 E - mo o ∂2 E/∂t 2 = 0
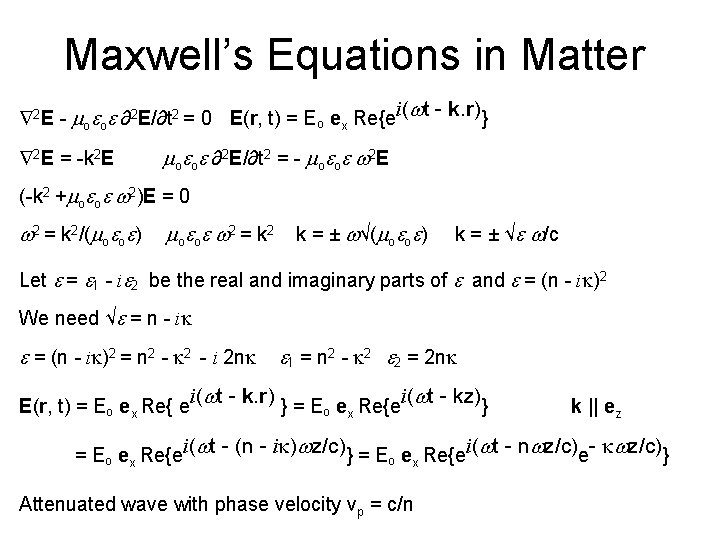
Maxwell’s Equations in Matter 2 E - mo o ∂2 E/∂t 2 = 0 E(r, t) = Eo ex Re{ei(wt - k. r)} 2 E = -k 2 E mo o ∂2 E/∂t 2 = - mo o w 2 E (-k 2 +mo o w 2)E = 0 w 2 = k 2/(mo o ) mo o w 2 = k 2 k = ± w√(mo o ) k = ± √ w/c Let = 1 - i 2 be the real and imaginary parts of and = (n - ik)2 We need √ = n - ik = (n - ik)2 = n 2 - k 2 - i 2 nk 1 = n 2 - k 2 2 = 2 nk E(r, t) = Eo ex Re{ ei(wt - k. r) } = Eo ex Re{ei(wt - kz)} k || ez = Eo ex Re{ei(wt - (n - ik)wz/c)} = Eo ex Re{ei(wt - nwz/c)e- kwz/c)} Attenuated wave with phase velocity vp = c/n
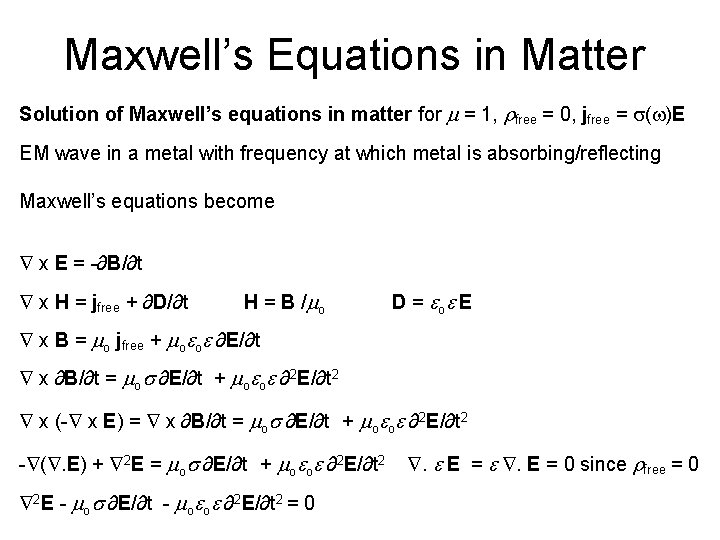
Maxwell’s Equations in Matter Solution of Maxwell’s equations in matter for m = 1, rfree = 0, jfree = s(w)E EM wave in a metal with frequency at which metal is absorbing/reflecting Maxwell’s equations become x E = -∂B/∂t x H = jfree + ∂D/∂t H = B /mo D = o E x B = mo jfree + mo o ∂E/∂t x ∂B/∂t = mos ∂E/∂t + mo o ∂2 E/∂t 2 x (- x E) = x ∂B/∂t = mos ∂E/∂t + mo o ∂2 E/∂t 2 - (. E) + 2 E = mos ∂E/∂t + mo o ∂2 E/∂t 2 . E = . E = 0 since rfree = 0 2 E - mos ∂E/∂t - mo o ∂2 E/∂t 2 = 0

Maxwell’s Equations in Matter 2 E - mos ∂E/∂t - mo o ∂2 E/∂t 2 = 0 E(r, t) = Eo ex Re{ei(wt - k. r)} 2 E = -k 2 E mos ∂E/∂t = mos iw E (-k 2 -mos iw +mo o w 2 )E = 0 k || ez mo o ∂2 E/∂t 2 = - mo o w 2 E s >> o w for a good conductor E(r, t) = Eo ex Re{ ei(wt - √(wsmo/2)z)e-√(wsmo/2)z} NB wave travels in +z direction and is attenuated The skin depth d = √(2/wsmo) is the thickness over which incident radiation is attenuated. For example, Cu metal DC conductivity is 5. 7 x 107 (Wm)-1 At 50 Hz d = 9 mm and at 10 k. Hz d = 0. 7 mm

Bound and Free Charges Bound charges All valence electrons in insulators (materials with a ‘band gap’) Bound valence electrons in metals or semiconductors (band gap absent/small ) Free charges Conduction electrons in metals or semiconductors Si ion Bound electron pair Mion k melectron k Mion Resonance frequency wo ~ (k/M)1/2 or ~ (k/m)1/2 Ions: heavy, resonance in infra-red ~1013 Hz Bound electrons: light, resonance in visible ~1015 Hz Free electrons: no restoring force, no resonance

Bound and Free Charges Bound charges Resonance model for uncoupled electron pairs Mion k melectron k Mion

Bound and Free Charges Bound charges In and out of phase components of x(t) relative to Eo cos(wt) Mion k melectron k Mion in phase out of phase

Bound and Free Charges Bound charges Connection to c and (w) Im{ (w)} w = wo w/wo Re{ (w)}

Bound and Free Charges Free charges Let wo → 0 in c and jpol = ∂P/∂t s(w) Re{ (w)} wo = 0 Drude ‘tail’ Im{s(w)} w

Energy in Electromagnetic Waves

Energy in Electromagnetic Waves

Energy in Electromagnetic Waves Energy density in plane electromagnetic waves in vacuum
 Maxwells equations
Maxwells equations Maxwell equation in matter
Maxwell equation in matter Maxwell equations
Maxwell equations Blger
Blger Maxwell equation based on faraday's law
Maxwell equation based on faraday's law Namblaa
Namblaa Gauss law
Gauss law Maxwell's equations in vacuum
Maxwell's equations in vacuum 9-3 practice polar and rectangular forms of equations
9-3 practice polar and rectangular forms of equations Translating chemical equations
Translating chemical equations Vacuum cleaner presentation
Vacuum cleaner presentation Hera.m
Hera.m Vacuum
Vacuum Barometer measures
Barometer measures Vacuum research corporation
Vacuum research corporation Vitmert
Vitmert Vacuum tube relay
Vacuum tube relay Mdi vacuum
Mdi vacuum Vcb contact resistance test
Vcb contact resistance test Condenser
Condenser Example of fully observable environment
Example of fully observable environment Caburn vacuum
Caburn vacuum Extreme high vacuum
Extreme high vacuum Vacuum tank design
Vacuum tank design Vacuum discale significato
Vacuum discale significato Present continuous vacuum
Present continuous vacuum Low pressure sewer system design
Low pressure sewer system design Mini vacuum cleaner project presentation
Mini vacuum cleaner project presentation Comparative vacuum monitoring
Comparative vacuum monitoring Vita lumin vacuum shade guide
Vita lumin vacuum shade guide Vacuum forming process steps
Vacuum forming process steps Mongodb lab
Mongodb lab Vacuum cavity
Vacuum cavity As the load on an engine increases the manifold
As the load on an engine increases the manifold Fueled by marcie hans
Fueled by marcie hans Pfitzner y kawaguchi
Pfitzner y kawaguchi Atomatoflames
Atomatoflames Herbert the vacuum
Herbert the vacuum