Lesson 12 Maxwells Equations Gauss Law Faradays Law













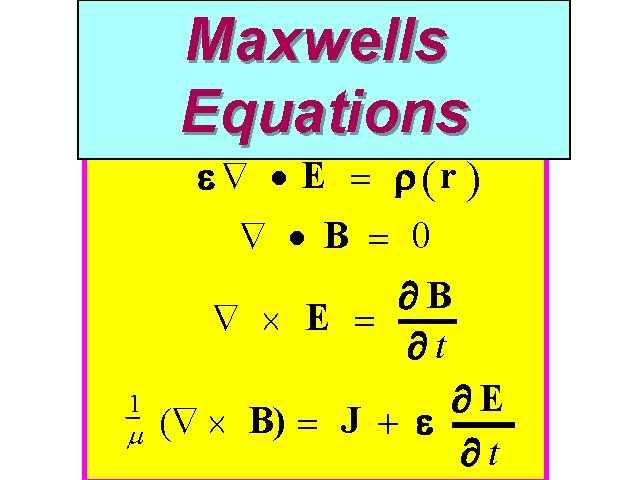
- Slides: 26

Lesson 12 Maxwells’ Equations ¨Gauss’ Law ¨Faradays’ Law ¨Ampere - Maxwell Law ¨Maxwells Equations ¨Integral Form ¨Differential Form

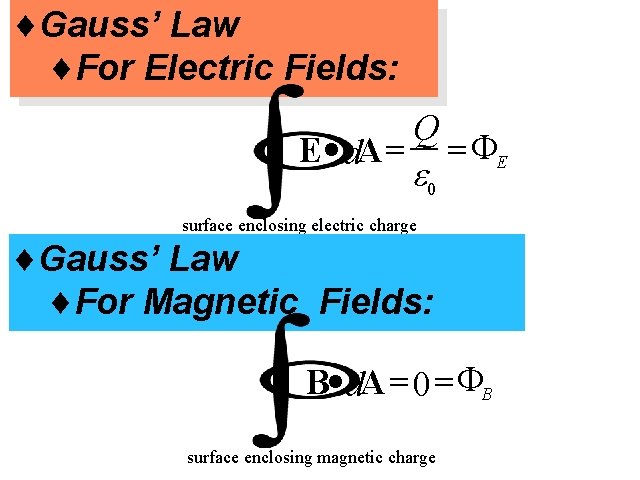
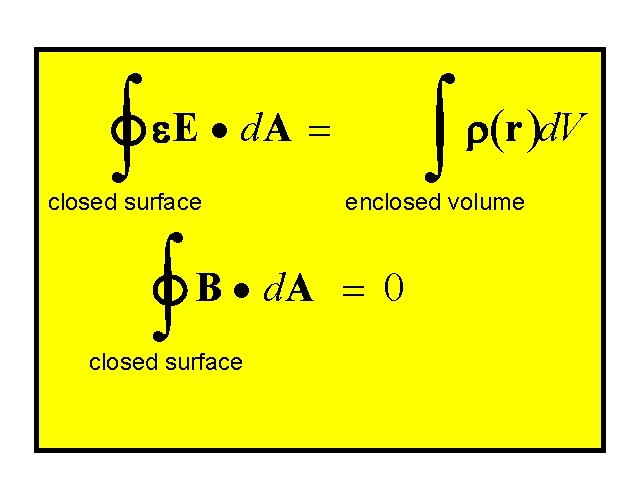
¨Gauss’ Law ¨For Electric Fields: Gauss' Law E · d. A = Q e 0 = FE surface enclosing electric charge ¨Gauss’ Law ¨For Magnetic Fields: B· d. A = 0 =FB surface enclosing magnetic charge

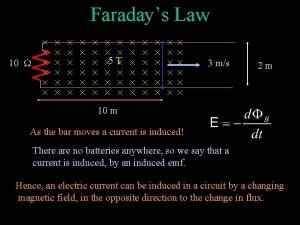
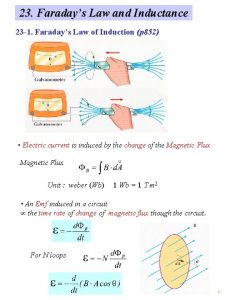
Amperes Law Amperes and Faradays Laws ò B · ds = m 0 I path enclosing current I B is due to I Faradays Law ò E · ds d. F B = dt path enclosing changing magnetic flux E is due to changing Flux

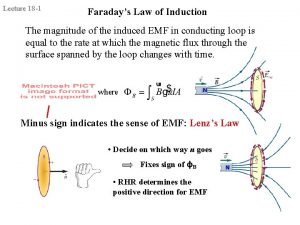
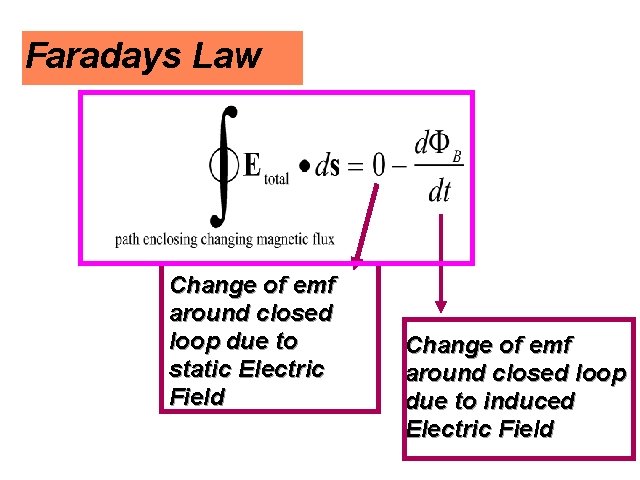
Faradays Law Change of emf around closed loop due to static Electric Field Change of emf around closed loop due to induced Electric Field

Changing Flux I Magnetic Flux Produces Induced Electric Field

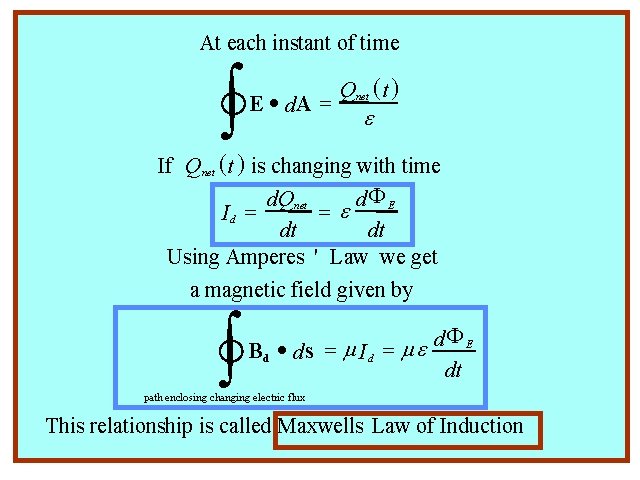
At each instant of time ò ( t )Induction Maxwells. ELaw Qof · d. A = net e If Q net (t ) is changing with time d. Qnet d. F E =e Id = dt dt Using Amperes ' Law we get a magnetic field given by ò FE d B d · d s = m I d = me dt path enclosing changing electric flux This relationship is called Maxwells Law of Induction

Changing Flux II Electric Flux Produces Induced Magnetic Field

We can thus generalize Amperes Law to look Ampere Maxwell Law exactly analogous to Faradays’ Law I
Displacement Current I

Displacement Current II Get varying electric fields in capacitors I c (t) + E(t)

s (t ) Q(t ) = E (t ) = Displacement e Current Ae (t ) Q F E (t ) = A = e Ae d. F E 1 d. Q d. F E d. Q = Ûe = e dt dt Þ Id (t ) = Ic (t ) III Id (t ) is the virtual displacement current between plates Can use Kirchoffs Rules for NON EQUILIBRIUM situation if one uses displacement current

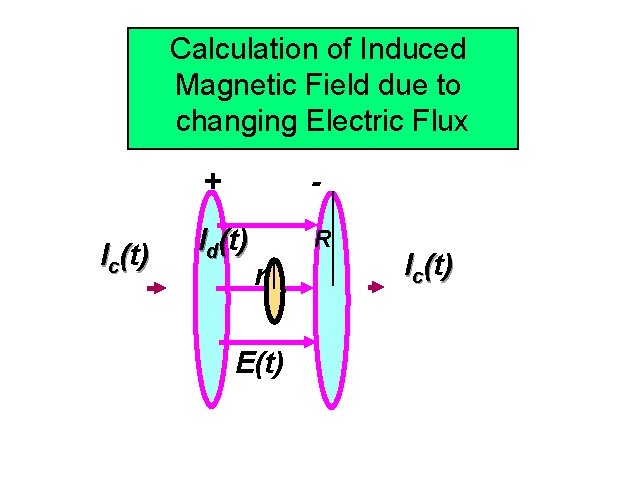
Calculation of Induced Magnetic Field due to Displacement Current changing Electric Flux I c (t) + - I d (t) R r E(t) I c (t) IV

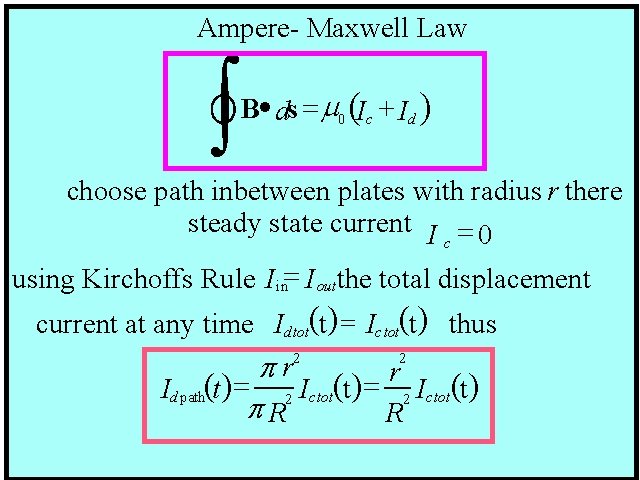
Ampere- Maxwell Law ò Ampere B- ·Maxwell Law II s =m ( + ) d 0 Ic Id choose path inbetween plates with radius r there steady state current I = 0 c using Kirchoffs Rule Iin= I outthe total displacement current at any time Id tot(t) = Ic tot(t) thus 2 2 pr r = = Id path(t) 2 Ic tot (t) p. R R

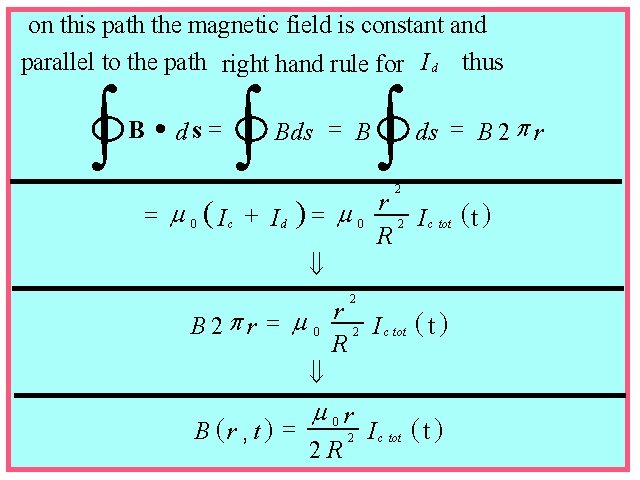
on this path the magnetic field is constant and parallel to the path right hand rule for I d thus Calculation of B field using Ampere Maxwell Law B · ds = B 2 p r ò ò = m 0 ( Ic + Id ò 2 )= m 0 r (t ) 2 I c tot R ß r p = m B 2 r 0 R 2 2 I c tot ( t ) ß B (r , t ) = m 0 r 2 R 2 I c tot ( t )

Maxwells Equations Integral form

Changing Electric Field Changing Fields Fluctuating electric and magnetic fields Electro-Magnetic Radiation Changing Magnetic Field

Speed of Light

Maxwells Lorentz. Equations Force PLUS the Lorentz Force completly describe the behaviour of electricity and magnetism

Maxwells Laws - Differential Form I Differential Form of Maxwells equations

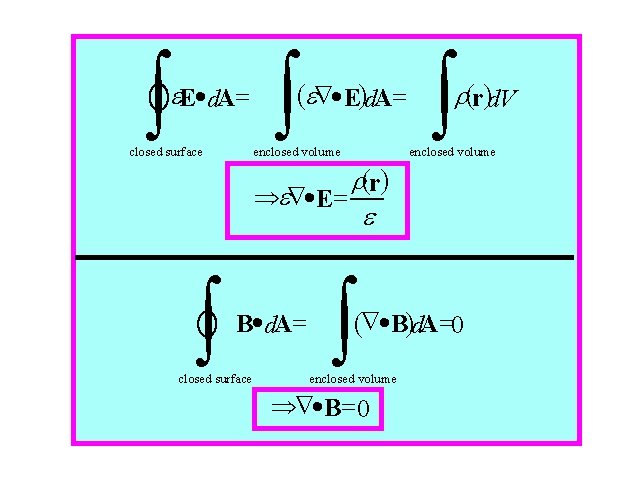
ò Derivation I e. E · d. A = closed surface ò enclosed volume B · d. A = 0 closed surface ò r(r )d. V

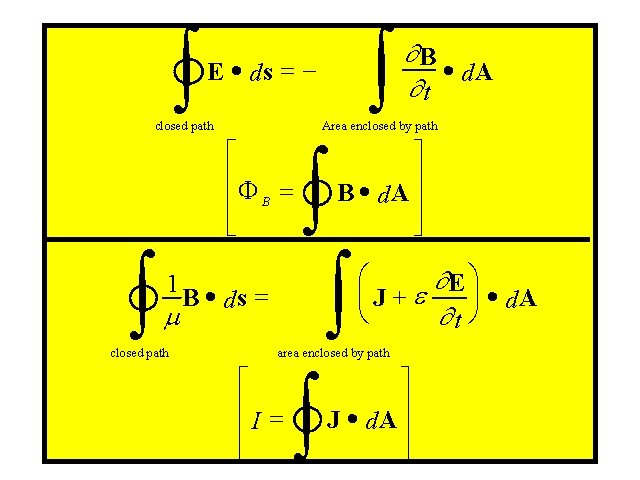
ò Derivationò ò ò E · ds = - closed path Area enclosed by path é êF = ê B êë 1 m closed path ¶B · d. A ¶t II ù ú · B d. A ú úû æ ¶E ö çJ+e ÷ · d. A è ¶t ø B · ds = area enclosed by path é ê = êI êë ù ú J · d. A ú úû

Vector Calculus

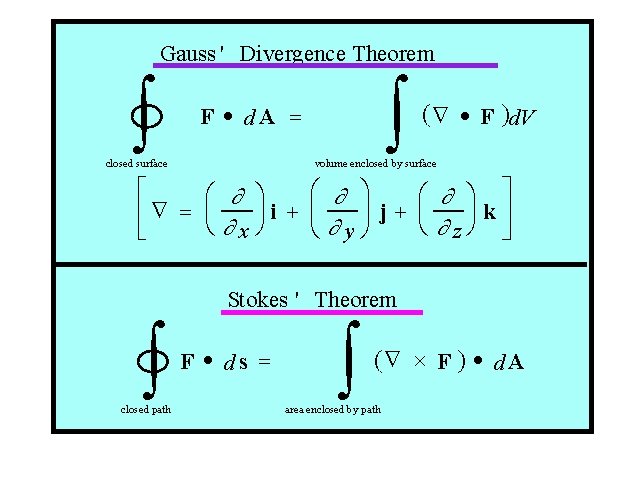
Gauss ' Divergence Theorem Gauss' and Stokes Theorems ò ò F · d. A = closed surface ( Ñ · F )d. V volume enclosed by surface é æ ¶ ö ù êÑ = ç ÷ j+ ç ÷i + ç ÷ kú è ¶xø è ¶zø û è ¶yø ë Stokes ' Theorem ò closed path F · ds = ò (Ñ ´ F ) · d A area enclosed by path

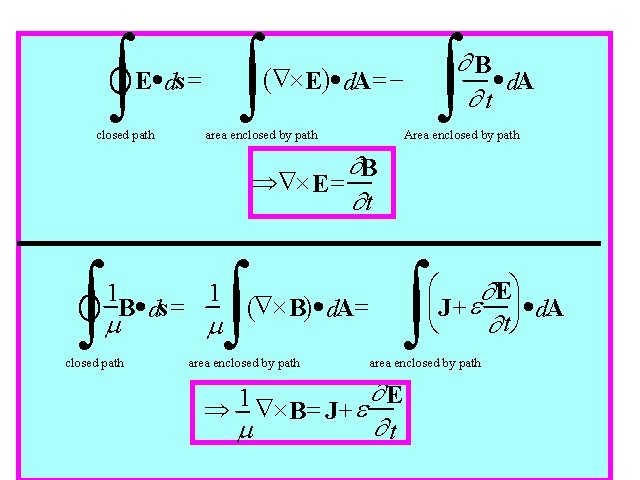
ò ò ò ¶B (Ñ´ E·Using E)· d. A= ds = Theorems I¶ t·d. A closed path area enclosed by path Area enclosed by path ¶B ÞÑ´ E = ¶t ò 1 1 · = B ds m closed path m ò (Ñ´ B)· d. A= area enclosed by path ò æ Eö ¶ çJ + e ÷ ·d. A è ¶ tø area enclosed by path ¶E 1 Þ Ñ´ B = J + e ¶t m

ò ò ò Using e. E·d. A= Theorems r. II (eÑ·E)d. A= (r)d. V closed surface enclosed volume r(r) ÞeÑ·E = e ò B·d. A= closed surface ò (Ñ·B)d. A=0 enclosed volume ÞÑ·B= 0
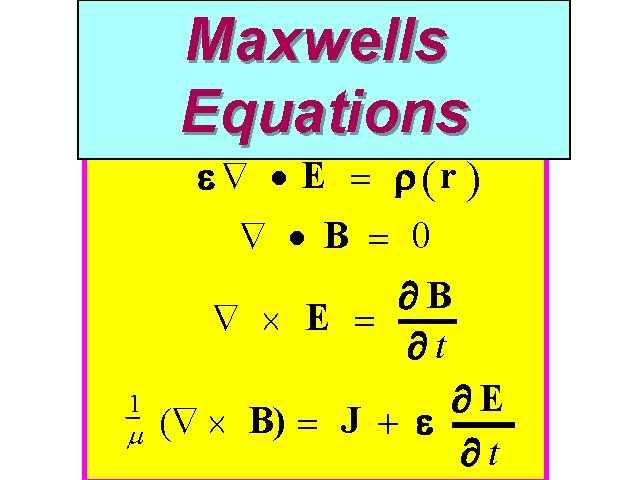
Maxwells Equations e Ñ · E = r (r ) Ñ · B = 0 ¶B Ñ ´ E = ¶t 1 m ¶E (Ñ ´ B) = J + e ¶t
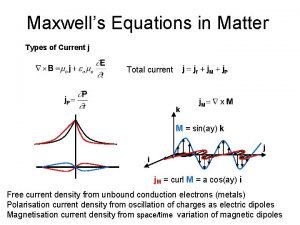
 Maxwells equations in matter
Maxwells equations in matter Maxwell equations
Maxwell equations Maxwells equations
Maxwells equations Lenz's law
Lenz's law Faraday law
Faraday law Faraday's law
Faraday's law Lenz law
Lenz law Gaussian elimination echelon form
Gaussian elimination echelon form Faraday buz kovası deneyi
Faraday buz kovası deneyi Maxwell correction to ampere's law
Maxwell correction to ampere's law Namblaa
Namblaa Ampere maxwell law
Ampere maxwell law Maxwells lover
Maxwells lover Faraday's constant
Faraday's constant Faradays lov
Faradays lov Are we getting
Are we getting Gauss law to coulomb's law
Gauss law to coulomb's law Derive coulomb's law from gauss law
Derive coulomb's law from gauss law Lesson 1 gauss in das haus
Lesson 1 gauss in das haus Differential form of gauss law
Differential form of gauss law Gauss law in dielectrics
Gauss law in dielectrics Charge density symbol name
Charge density symbol name Gauss law in gravitation
Gauss law in gravitation Fundamental laws of magnetostatics
Fundamental laws of magnetostatics Qualitative statement
Qualitative statement Gauss law cube example
Gauss law cube example Surface integral of electric field
Surface integral of electric field