Mathematics Session 1 Trigonometric ratios and Identities Topics

Mathematics

Session 1 Trigonometric ratios and Identities

Topics Measurement of Angles Definition and Domain and Range of Trigonometric Function Compound Angles Transformation of Angles

Measurement of Angles J 001 B O A Angle is considered as the figure obtained by rotating initial ray about its end point.

Measure and Sign of an Angle J 001 Measure of an Angle : - Amount of rotation from initial side to terminal side. Sign of an Angle : B O A Rotation anticlockwise – Angle positive Rotation clockwise – B’ Angle negative

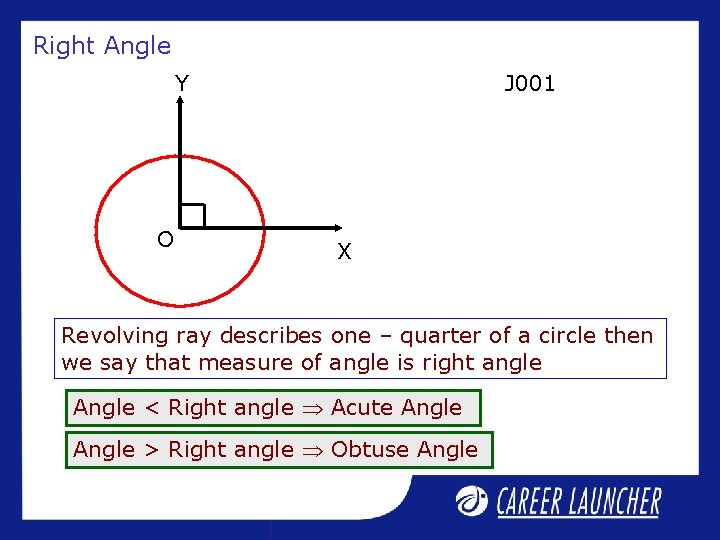
Right Angle J 001 Y O X Revolving ray describes one – quarter of a circle then we say that measure of angle is right angle Angle < Right angle Acute Angle > Right angle Obtuse Angle

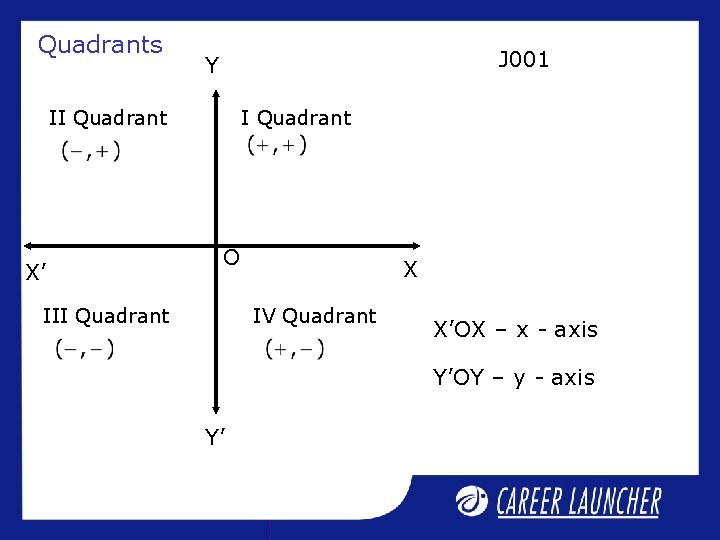
Quadrants J 001 Y II Quadrant X’ I Quadrant O III Quadrant X IV Quadrant X’OX – x - axis Y’OY – y - axis Y’

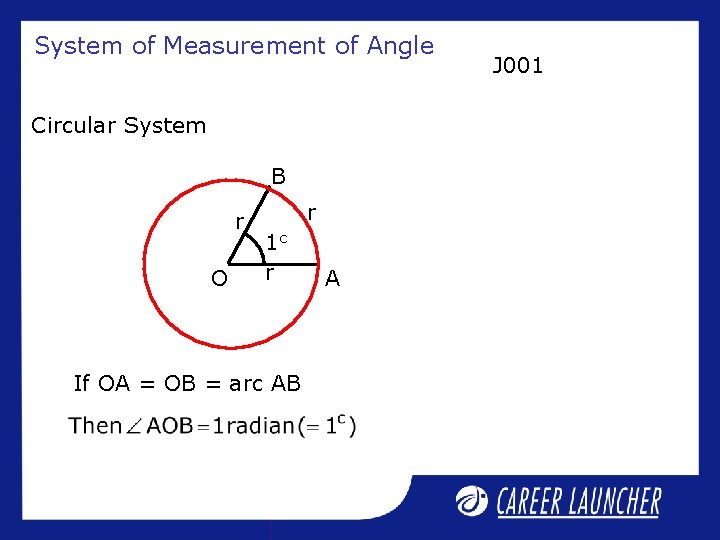
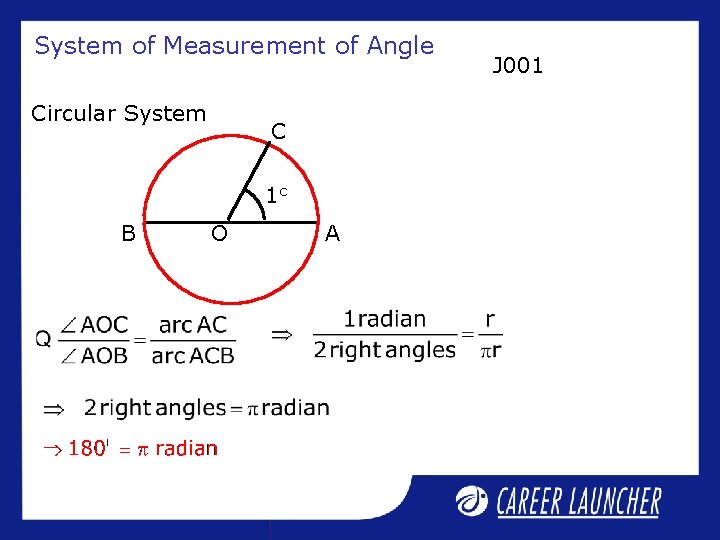
System of Measurement of Angle J 001 Measurement of Angle Sexagesimal System Centesimal System or or British System French System Circular System or Radian Measure

System of Measurement of Angles J 001 Sexagesimal System (British System) 1 right angle = 90 degrees (=90 o) 1 degree = 60 minutes (=60’) 1 minute = 60 seconds (=60”) Centesimal System (French System) 1 right angle = 100 grades (=100 g) 1 grade = 100 minutes (=100’) 1 minute = 100 Seconds (=100”) Is 1 minute of sexagesimal = 1 minute of centesimal ? NO

System of Measurement of Angle Circular System B r O r 1 c r If OA = OB = arc AB A J 001

System of Measurement of Angle Circular System C 1 c B O A J 001

Relation Between Degree Grade And Radian Measure of An Angle OR J 002

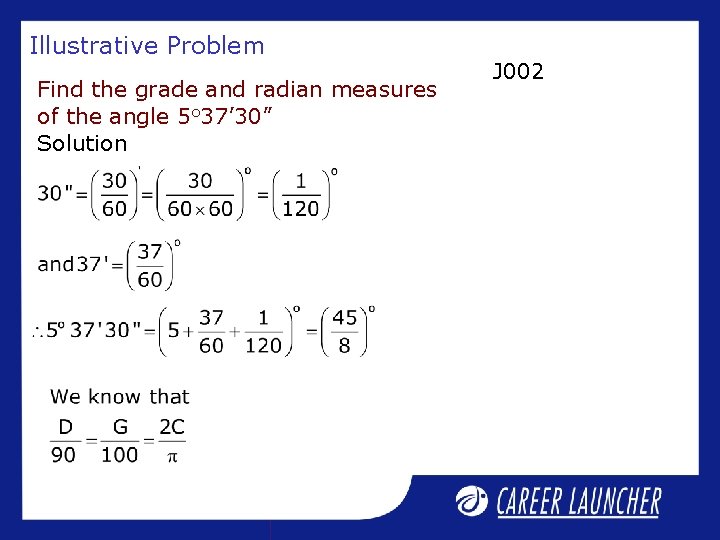
Illustrative Problem Find the grade and radian measures of the angle 5 o 37’ 30” Solution J 002

Illustrative Problem Find the grade and radian measures of the angle 5 o 37’ 30” Solution J 002

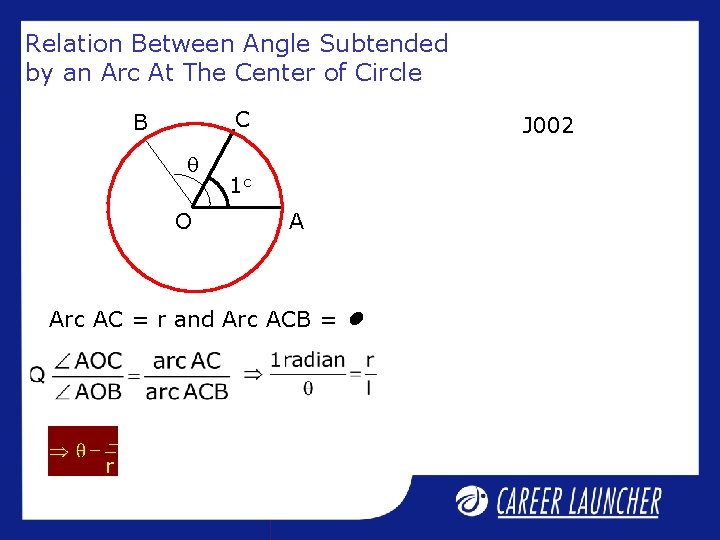
Relation Between Angle Subtended by an Arc At The Center of Circle C B O J 002 1 c A Arc AC = r and Arc ACB =

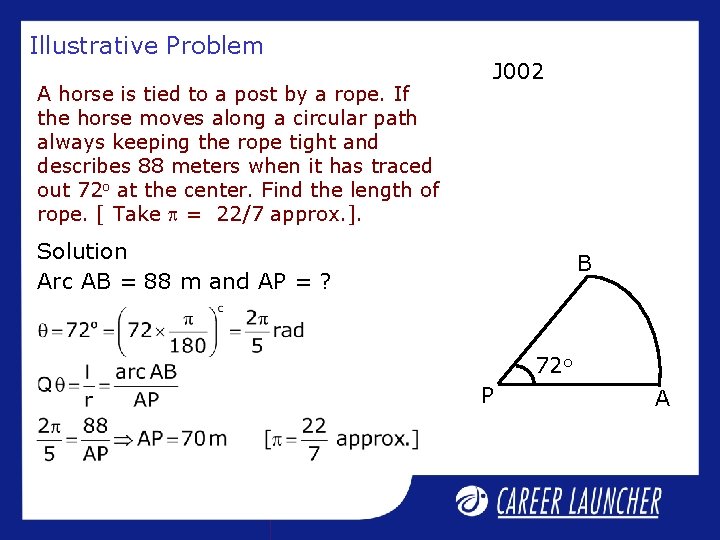
Illustrative Problem A horse is tied to a post by a rope. If the horse moves along a circular path always keeping the rope tight and describes 88 meters when it has traced out 72 o at the center. Find the length of rope. [ Take = 22/7 approx. ]. J 002 Solution Arc AB = 88 m and AP = ? B 72 o P A

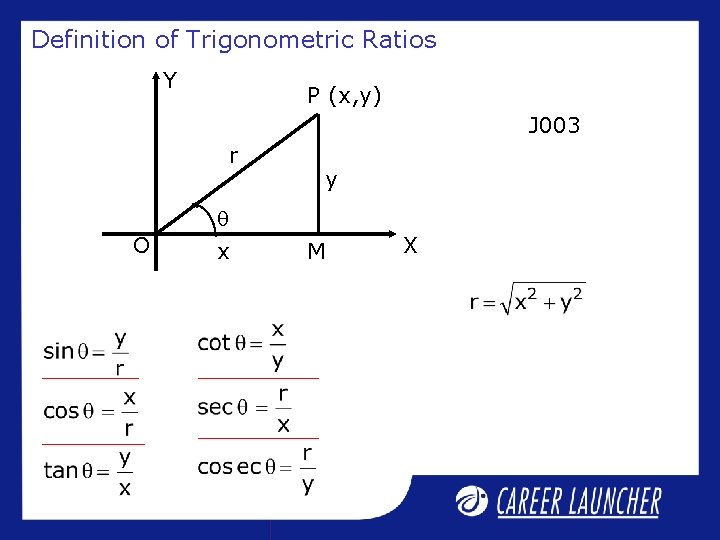
Definition of Trigonometric Ratios Y P (x, y) J 003 r y O x M X

Some Basic Identities

Illustrative Problem J 003 Solution

Signs of Trigonometric Function In All Quadrants In First Quadrant Y P (x, y) r y O J 004 x M Here x >0, y>0, X >0

Signs of Trigonometric Function In All Quadrants J 004 In Second Quadrant Y P (x, y) y X’ r x Y’ X Here x <0, y>0, >0

Signs of Trigonometric Function In All Quadrants In Third Quadrant Y M X’ O P (x, y) Y’ J 004 X Here x <0, y<0, >0

Signs of Trigonometric Function In All Quadrants J 004 In Fourth Quadrant O M X P (x, y) Y’ Here x >0, y<0, >0

Signs of Trigonometric Function In All Quadrants Y I Quadrant All Positive II Quadrant sin & cosec are Positive X’ O X III Quadrant IV Quadrant tan & cot are Positive cos & sec are Positive Y’ ASTC : - All Sin Tan Cos J 004

Illustrative Problem If cot = lies in second quadrant, find the values of other five trigonometric function Solution Method : 1 J 004

Illustrative Problem lies in second If cot = quadrant, find the values of other five trigonometric function Solution Method : 2 P (-12, 5) 5 X’ Y r -12 Y’ X Here x = -12, y = 5 and r = 13 J 004

Domain and Range of Trigonometric Functions Domain Range sin R [-1, 1] cos R [-1, 1] tan cot R R sec R-(-1, 1) cosec R-(-1, 1) J 005

Illustrative problem Prove that is possible for real values of x and y only when x=y Solution But for real values of x and y is not less than zero J 005

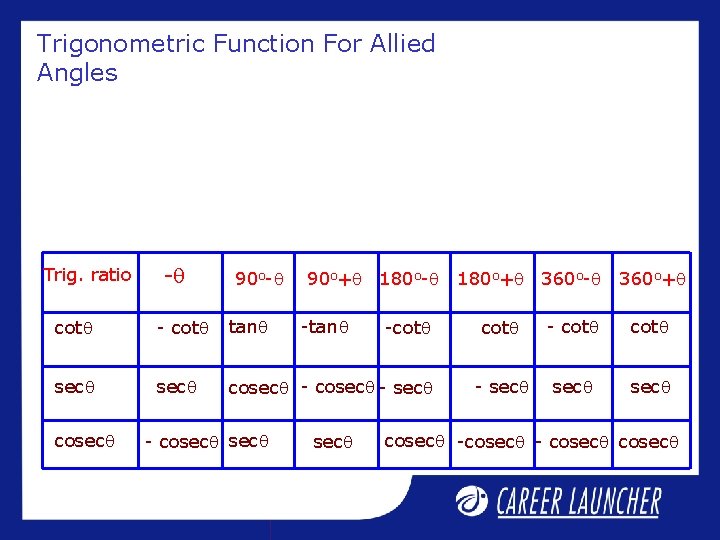
Trigonometric Function For Allied Angles If angle is multiple of 900 then sin cos; tan cot; sec cosec If angle is multiple of 1800 then sin; cos; tan etc. Trig. ratio - 90 o+ 180 o- 180 o+ 360 o- 360 o+ sin - sin cos sin - cos cos tan - tan cot -tan - tan

Trigonometric Function For Allied Angles Trig. ratio - 90 o+ 180 o- cot - cot tan sec cosec - sec cosec -tan sec -cot 180 o+ 360 o- 360 o+ cot - sec cosec - cosec

Periodicity of Trigonometric Function If f(x+T) = f(x) x, then T is called period of f(x) if T is the smallest possible positive number J 005 Periodicity : After certain value of x the functional values repeats itself Period of basic trigonometric functions sin (360 o+ ) = sin period of sin is 360 o or 2 cos (360 o+ ) = cos period of cos is 360 o or 2 tan (180 o+ ) = tan period of tan is 180 o or

Trigonometric Ratio of Compound Angles of the form of A+B, A-B, A+B+C, A-B+C etc. are called compound angles (I) The Addition Formula sin (A+B) = sin. Acos. B + cos. Asin. B cos (A+B) = cos. Acos. B - sin. Asin. B J 006

Trigonometric Ratio of Compound Angle We get Proved J 006

Illustrative problem Find the value of (i) sin 75 o (ii) tan 105 o Solution (i) Sin 75 o = sin (45 o + 30 o) = sin 45 o cos 30 o + cos 45 o sin 30 o

Trigonometric Ratio of Compound Angle (I) The Difference Formula sin (A - B) = sin. Acos. B - cos. Asin. B cos (A - B) = cos. Acos. B + sin. Asin. B Note : - by replacing B to -B in addition formula we get difference formula

Illustrative problem If tan ( + ) = a and tan ( - ) = b Prove that Solution

Some Important Deductions sin (A+B) sin (A-B) = sin 2 A - sin 2 B = cos 2 B - cos 2 A cos (A+B) cos (A-B) = cos 2 A - sin 2 B = cos 2 B - sin 2 A

To Express acos + bsin in the form kcos or sin acos +bsin Similarly we get acos + bsin = sin

Illustrative problem Find the maximum and minimum values of 7 cos + 24 sin Solution 7 cos +24 sin

Illustrative problem Find the maximum and minimum value of 7 cos + 24 sin Solution Max. value =25, Min. value = -25 Ans.

Transformation Formulae Transformation of product into sum and difference 2 sin. Acos. B = sin(A+B) + sin(A - B) 2 cos. Asin. B = sin(A+B) - sin(A - B) 2 cos. Acos. B = cos(A+B) + cos(A - B) Proof : - R. H. S = cos(A+B) + cos(A - B) = cos. Acos. B - sin. Asin. B+cos. Acos. B+sin. Asin. B = 2 cos. Acos. B =L. H. S 2 sin. Asin. B = cos(A - B) - cos(A+B) [Note]

Transformation Formulae Transformation of sums or difference into products By putting A+B = C and A-B = D in the previous formula we get this result or Note

Illustrative problem Prove that Solution Proved

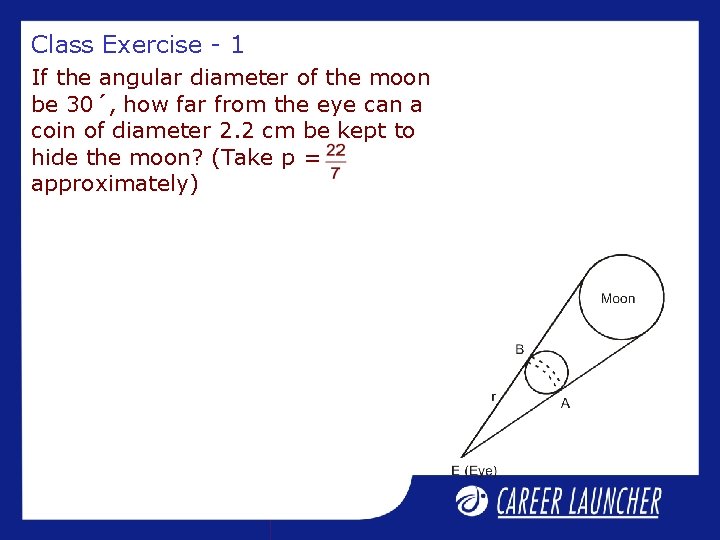
Class Exercise - 1 If the angular diameter of the moon be 30´, how far from the eye can a coin of diameter 2. 2 cm be kept to hide the moon? (Take p = approximately)

Class Exercise - 1 If the angular diameter of the moon be 30´, how far from the eye can a coin of diameter 2. 2 cm be kept to hide the moon? (Take p = approximately) Solution : Let the coin is kept at a distance r from the eye to hide the moon completely. Let AB = Diameter of the coin. Then arc AB = Diameter AB = 2. 2 cm

Class Exercise - 2 Prove that tan 3 A tan 2 A tan. A = tan 3 A – tan 2 A – tan. A. Solution : We have 3 A = 2 A + A tan 3 A = tan(2 A + A) tan 3 A = tan 3 A – tan 3 A tan 2 A tan. A = tan 2 A + tan. A tan 3 A – tan 2 A – tan. A = tan 3 A tan 2 A tan. A (Proved)

Class Exercise - 3 If sin = sin and cos = cos , then (a) (b) (c) (d) Solution : and

Class Exercise - 4 Prove that Solution: LHS = sin 20° sin 40° sin 60° sin 80°

Class Exercise - 4 Prove that Solution: - Proved.

Class Exercise - 5 Prove that Solution : -

Class Exercise - 5 Prove that Solution : -

Class Exercise - 6 The maximum value of 3 cosx + 4 sinx + 5 is (b) 9 (a) 5 (c) 7 Solution : - (d) None of these

Class Exercise - 6 The maximum value of 3 cosx + 4 sinx + 5 is Solution : - Maximum value of the given expression = 10.

Class Exercise - 7 If a and b are the solutions of a cos + b sin = c, then show that Solution : We have … (i) are roots of equatoin (i),

Class Exercise - 7 If a and b are the solutions of acos + bsin = c, then show that Solution : sin and sin are roots of equ. Hence Again from (i), (ii).

Class Exercise - 7 If a and b are the solutions of acos + bsin = c, then show that Solution : - (iv) and be the roots of equation (i), cos and cos are the roots of equation (iv). Now

Class Exercise - 8 If a seca – c tana = d and b seca + d tana = c, then (a) a 2 + b 2 = c 2 + d 2 + cd (b) (c) a 2 + b 2 = c 2 + d 2 (d) ab = cd

Class Exercise - 8 If a seca – c tana = d and b seca + d tana = c, then Solution : - …. . (I) Again Squaring and adding (i) and (ii), we get …. . ii

Class Exercise -9 The value of (a) 2 sin. A (b) (c) 2 cos. A (d)

Class Exercise -9 The value of Solution : -

Class Exercise -10 If , , and lie between 0 and of tan 2 is (b) (a) 1 (c) 0 Solution : - , then value (d) and between 0 and , Consequently, cos( - ) and sin( + ) are positive.

Class Exercise -10 If , and lie between 0 and of tan 2 is Solution : - , , then value