Verifying Trigonometric Identities OBJECTIVE VERIFY TRIGONOMETRIC IDENTITIES INTRODUCTION

Verifying Trigonometric Identities • OBJECTIVE: VERIFY TRIGONOMETRIC IDENTITIES

INTRODUCTION � One major aspect that people remember about Trigonometry, if they studied it in school, is the time they spent proving identities – making one side of an equation match the other. Many people love these little puzzles. The challenge, followed by success, can be a real thrill. Others, though, find this task of proving identities to be less than exciting. � Why do you need to prove identities? Don’t you know that they’re correct if they’re called identities? Sure you do, but proving them is still helpful down the road when you’re solving complex trig problems, because the process to solving them is all in the preparation. Many of the trig expressions that you use to solve practical problems have rather complicated and nasty-looking terms. By doing substitutions and manipulations with the trig identities, you can make those expressions more usable. All this practice with proving identities prepares you and gives you a heads-up as to what’s possible.

INTRODUCTION � Verifying trigonometric identities is a useful process when you need to convert a trigonometric expression into a form that is more useful algebraically. When you verify an identity, you cannot assume that the two sides of the equation are equal because you are trying to verify that they are equal. As a result, when verifying identities, you cannot use operations such as adding the same quantity to each side of the equation or cross multiplication. � Although there are similarities, verifying that a trigonometric equation is an identity is quite different from solving an equation. There is no well-defined set of rules to follow in verifying trigonometric identities, and it is best to learn the process by practicing.

Guidelines for Verifying Trigonometric Identities � Work with one side of the equation at a time. It is often better to work with the more complicated side first. Choose the side with the greater number of terms Choose the side with terms other than sine or cosine � Look for opportunities to factor an expression, add fractions, square a binomial, or create a monomial denominator � Look for opportunities to use the fundamental identities. Note which functions are in the final expression you want. Sines and cosines pair up well, as do secants and tangents, and cosecants and cotangents. � If the preceding guidelines do not help, try converting all terms to sines and cosines � Always try something. Even making an attempt that leads to a dead end can provide insight

EX: Verify the identity � 1.

EX: Verify the identity � 2.

EX: Verify the identity � 3.

EX: Verify the identity � 4.
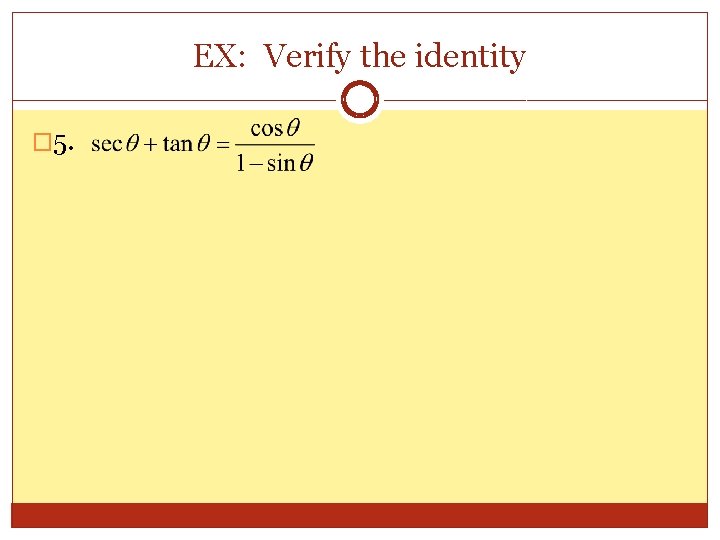
EX: Verify the identity � 5.
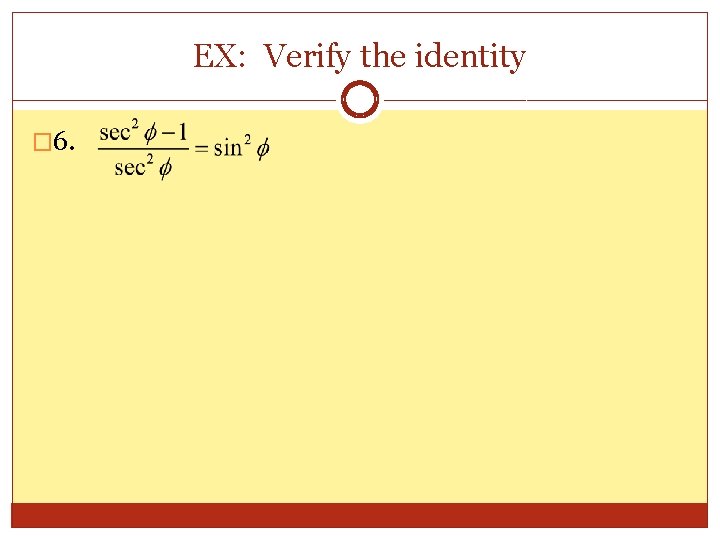
EX: Verify the identity � 6.
- Slides: 10

















