Chapter 5 Trigonometric Identities Section 5 1 Fundamental

Chapter 5 Trigonometric Identities Section 5. 1 Fundamental Identities Section 5. 2 Verifying Identities Section 5. 3 Cos Sum and Difference Section 5. 4 Sin & Tan Sum and Dif Section 5. 5 Double-Angle Identities Section 5. 6 Half-Angle Identities

Section 5. 1 Fundamental Identities • Review of basic Identities • Negative-Angle Identities • Fundamental Identities

x r = nu se te po Hy tan θ = y x A θ adjacent side = x opposite side = y cos θ = r sin θ = y r

csc θ = r y B r x r = se nu te po Hy cot θ = x y A θ adjacent side = x opposite side = y sec θ = C

The Reciprocal Identities sin £ = 1 csc £ = csc £ 1 sin £ cos £ = 1 sec £ = sec £ 1 cos £ tan £ = 1 cot£ £ = cot 1 tan £

The quotient Identities tan £ = sin £ = cos £ y x cot £ = cos £ = sin £ x y

The Negative-Angle Identities sin(-£) = - sin £ cos(-£) = cos £ tan(-£) = - tan £

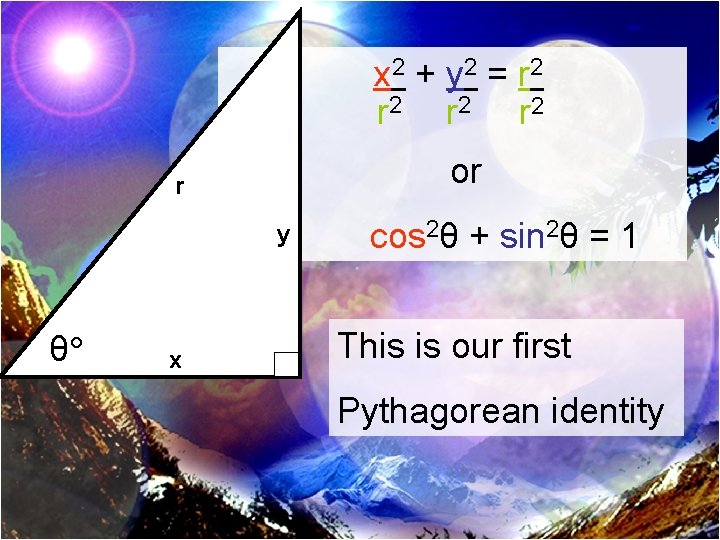
x 2 + y 2 = r 2 r 2 or r y θ x cos 2θ + sin 2θ = 1 This is our first Pythagorean identity

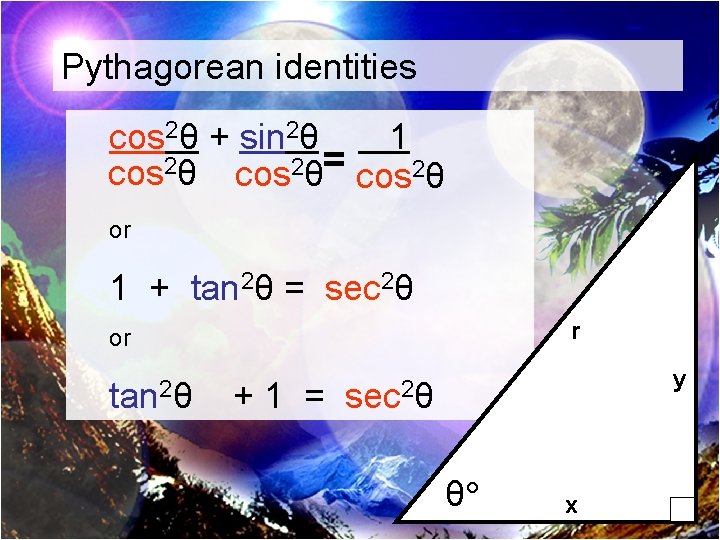
Pythagorean identities cos 2θ + sin 2θ 1 cos 2θ= cos 2θ or 1 + tan 2θ = sec 2θ r or tan 2θ +1 = y sec 2θ θ x

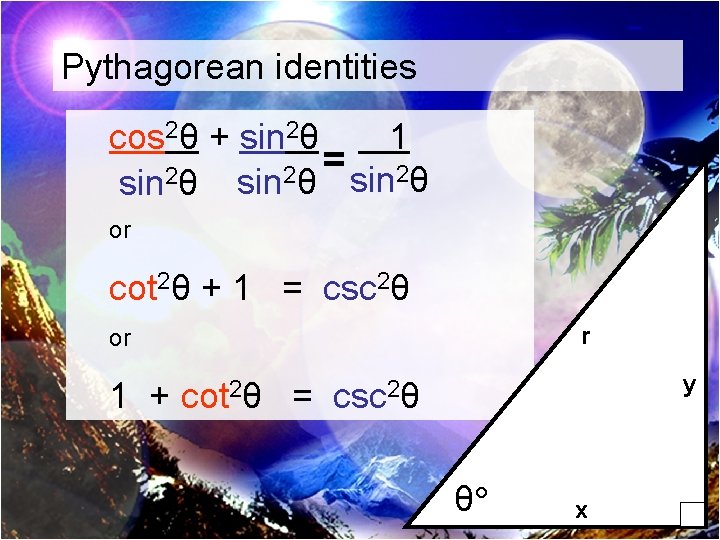
Pythagorean identities cos 2θ + sin 2θ 1 = sin 2θ 2 2 sin θ or cot 2θ + 1 = csc 2θ r or 1 + cot 2θ = y csc 2θ θ x

Section 5. 2 Verifying Identities • Verify Identities by Working with One Side • Verify Identities by Working with Two Sides

Hints for Verifying Identities • Learn the fundamental identities and their equivalent forms. • Simplify using sin and cos. • Keep in mind the basic algebra applies to trig functions. • You can always go down to x, y, and r

Section 5. 3 Cos Sum & Difference • • Difference Identity for Cosine Sum Identity for Cosine Co-function Identities Applying the Sum and Difference Identities

Cosine of the Sum or Difference cos(A + B) = cos A cos B – sin A sin B cos(A - B) = cos A cos B + sin A sin B

Co-function Identities sin (90à - £à) = cos £à cos (90à - £à) = sin £à tan (90à - £à) = cot £à csc (90à - £à) = sec £à sec (90à - £à) = csc £à cot (90à - £à) = tan £à

Section 5. 4 Sine and Tangent Sum and Difference Identities • Sum Identity for Sine • Difference Identity for Sine • Applying the Sum and Difference Identities for Sine

Sine of the Sum or Difference sin(A + B) = sin A cos B + cos A sin B sin(A - B) = sin A cos B - cos A sin B

Tangent of the Sum or Difference tan (A + B) = tan (A - B) = tan A + tan B 1 – tan A tan B tan A - tan B 1 + tan A tan B

Section 5. 5 Double-Angle Identities • Verifying Identities with Double Angels • Applying Double-Angle Identities

Double-Angle Identity Cosine cos(2 A) = cos(A+A) = cos A – sin A = cos 2 A – sin 2 A or cos(2 A) = cos 2 A – sin 2 A = (1 - sin 2 A) – sin 2 A = 1 - 2 sin 2 A or 2 cos 2 A - 1

Double-Angle Identity Sine sin(2 A) = sin(A+A) = sin A cos A + cos A sin A = 2 sin A cos A

Double-Angle Identity Tangent tan A + tan A tan 2 A = tan (A + A) = 1 – tan A 2 tan A = 1 – tan 2 A

Section 5. 6 Half-Angle Identities • Half-Angel Identities • Using the Half-Angle Identities

Half-Angle Identity Sine cos 2 A = 1 - 2 sin 2 A -cos 2 A 0 = 1 - 2 sin 2 A – cos 2 A - 2 sin 2 A -2 sin 2 A = 1 – cos 2 A sin 2 A = (cos 2 A – 1) 2

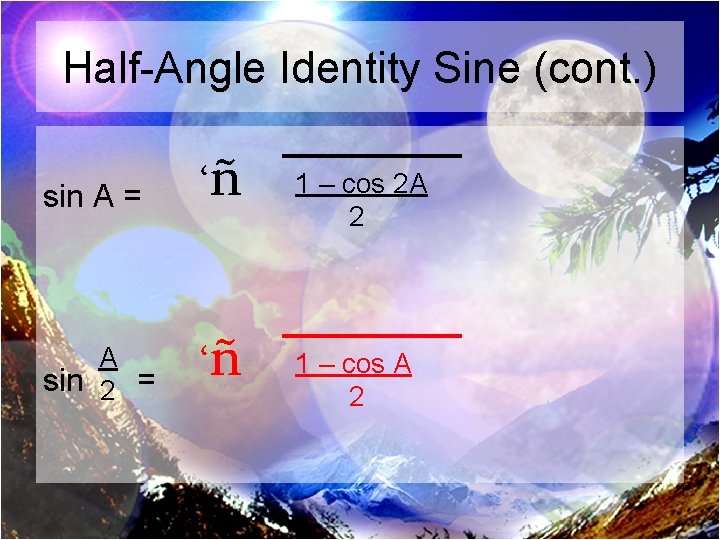
Half-Angle Identity Sine (cont. ) sin A = ‘ñ 1 – cos 2 A 2 A sin 2 = ‘ñ 1 – cos A 2

Half-Angle Identity Cosine cos 2 A = 2 cos 2 A - 1 +1 +1 cos 2 A + 1 = 2 cos 2 A = 1 + cos 2 A cos 2 A = (1 + cos 2 A) 2

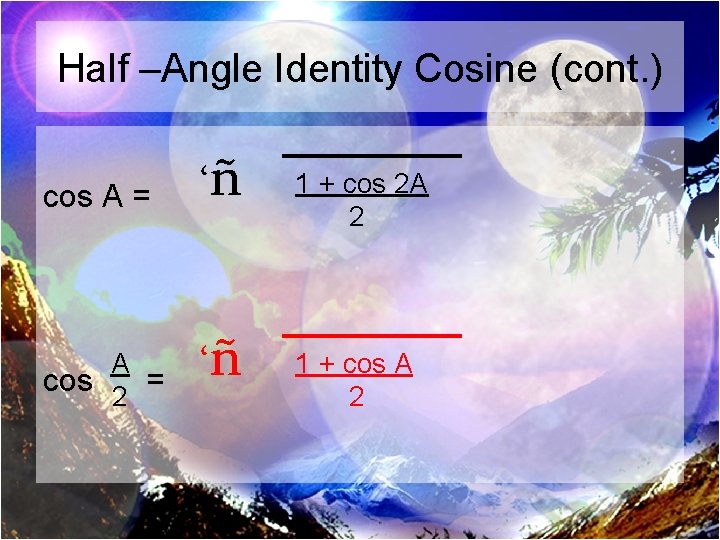
Half –Angle Identity Cosine (cont. ) cos A = ‘ñ 1 + cos 2 A 2 A cos 2 = ‘ñ 1 + cos A 2

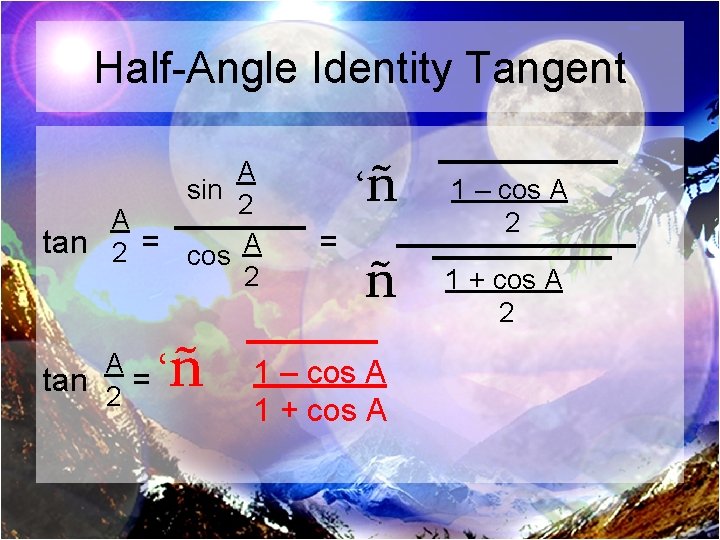
Half-Angle Identity Tangent A sin 2 A tan 2 = cos A 2 A tan 2 = ‘ñ ñ 1 – cos A 1 + cos A 1 – cos A 2 1 + cos A 2

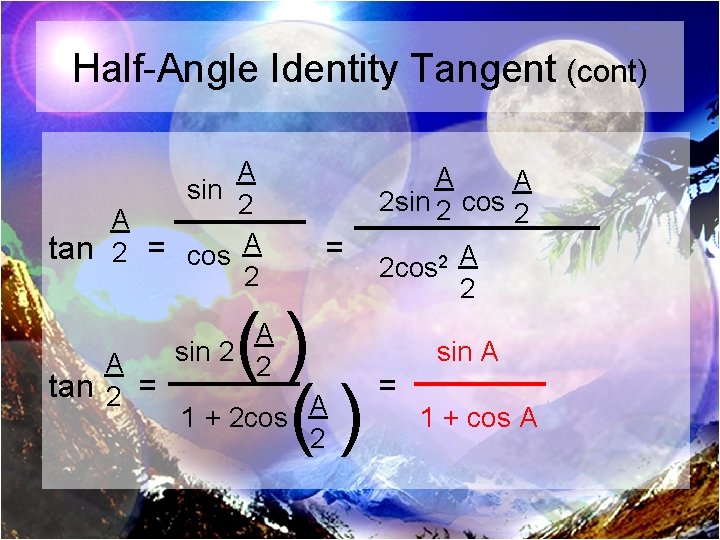
Half-Angle Identity Tangent (cont) A sin 2 A tan 2 = cos A 2 A tan 2 = A A 2 sin 2 cos 2 = () () A sin 2 2 1 + 2 cos A 2 2 cos 2 A 2 sin A = 1 + cos A

Half-Angle Identity Tangent (cont) Using the other formula we get: 1 - cos A A tan 2 = sin A