LESSON 5 1 Trigonometric Identities FiveMinute Check over

LESSON 5– 1 Trigonometric Identities

Five-Minute Check (over Chapter 4) TEKS Then/Now New Vocabulary Key Concept: Reciprocal and Quotient Identities Example 1: Use Reciprocal and Quotient Identities Key Concept: Pythagorean Identities Example 2: Use Pythagorean Identities Key Concept: Cofunction Identities Key Concept: Odd-Even Identities Example 3: Use Cofunction and Odd-Even Identities Example 4: Simplify by Rewriting Using Only Sine and Cosine Example 5: Simplify by Factoring Example 6: Simplify by Combining Fractions Example 7: Rewrite to Eliminate Fractions

Over Chapter 4 Find the exact values of the six trigonometric functions of θ. A. B. C. D.

Over Chapter 4 If , find the exact values of the five remaining trigonometric function values of θ. A. B. C. D.

Over Chapter 4 Write − 150° in radians as a multiple of π. A. B. C. D.

Over Chapter 4 Solve ∆ABC if A = 33°, b = 9, and c = 13. Round side lengths to the nearest tenth and angle measures to the nearest degree. A. B = 42°, C = 105°, a = 7. 3 B. B = 52°, C = 95°, a = 9 C. B = 95°, C = 52°, a = 7. 3 D. B = 105°, C = 42°, a = 7. 3

Over Chapter 4 Find the exact value of A. B. C. D.

Targeted TEKS P. 5(M) Use trigonometric identities such as reciprocal, quotient, Pythagorean, cofunctions, even/odd, and sum and difference identities for cosine and sine to simplify trigonometric expressions. Mathematical Processes P. 1(D), P. 1(E)

You found trigonometric values using the unit circle. (Lesson 4 -3) • Identify and use basic trigonometric identities to find trigonometric values. • Use basic trigonometric identities to simplify and rewrite trigonometric expressions.

• identity • trigonometric identity • cofunction

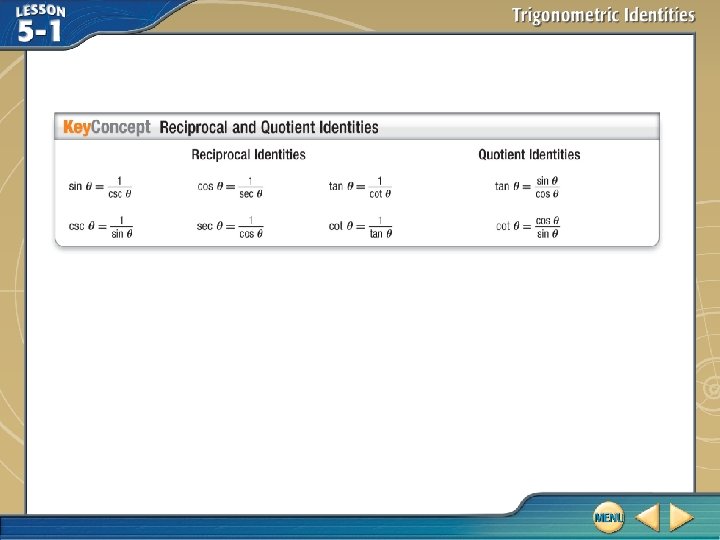
Use Reciprocal and Quotient Identities A. If , find sec θ. Reciprocal Identity Divide. Answer:

Use Reciprocal and Quotient Identities B. If and , find sin x. Reciprocal Identity Quotient Identity Substitute for cos x.

Use Reciprocal and Quotient Identities Divide. Multiply each side by Simplify. Answer: .

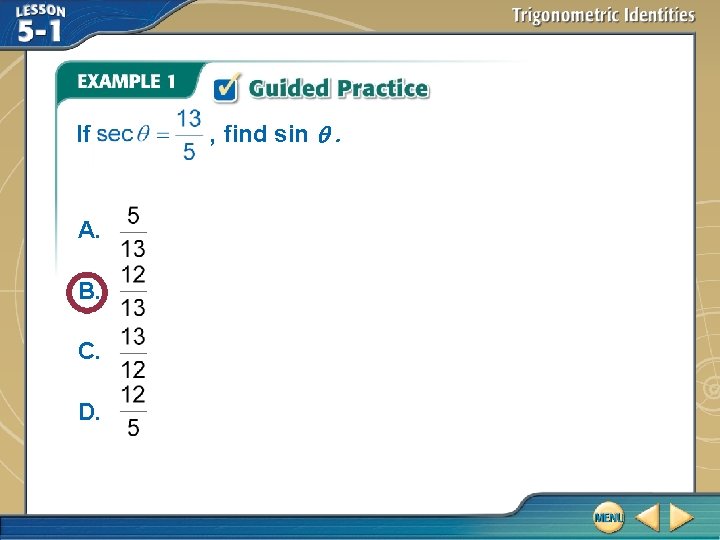
If A. B. C. D. , find sin .

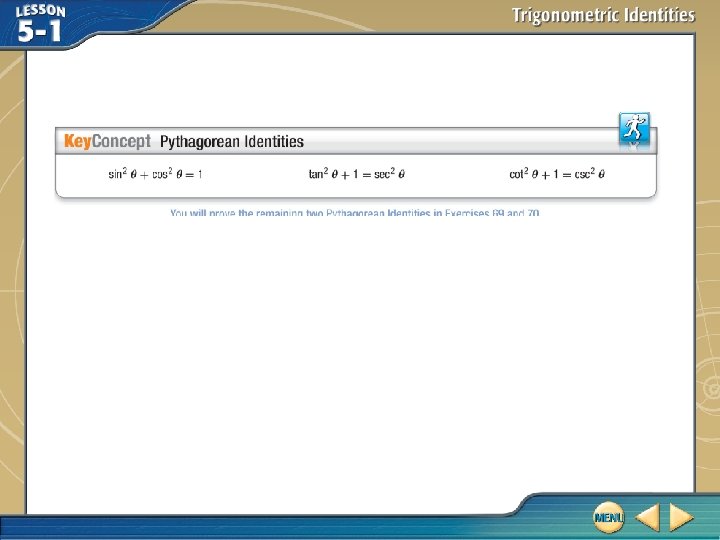
Use Pythagorean Identities If cot θ = 2 and cos θ < 0, find sin θ and cos θ. Use the Pythagorean Identity that involves cot θ. cot 2 θ + 1 = csc 2 θ Pythagorean Identity (2) 2 + 1 = csc 2 θ cot θ = 2 5 = csc 2 θ Simplify. = csc θ Take the square root of each side. Reciprocal Identity Solve for sin θ.

Use Pythagorean Identities Since is positive and cos θ < 0, sin θ must be negative. So . You can then use this quotient identity again to find cos θ. Quotient Identity cot θ = 2 and Multiply each side by .

Use Pythagorean Identities So, Answer: Check sin 2 θ + cos 2 θ = 1 Simplify. Pythagorean Identity

Find the value of csc and cot if cos < 0. A. B. C. D. and

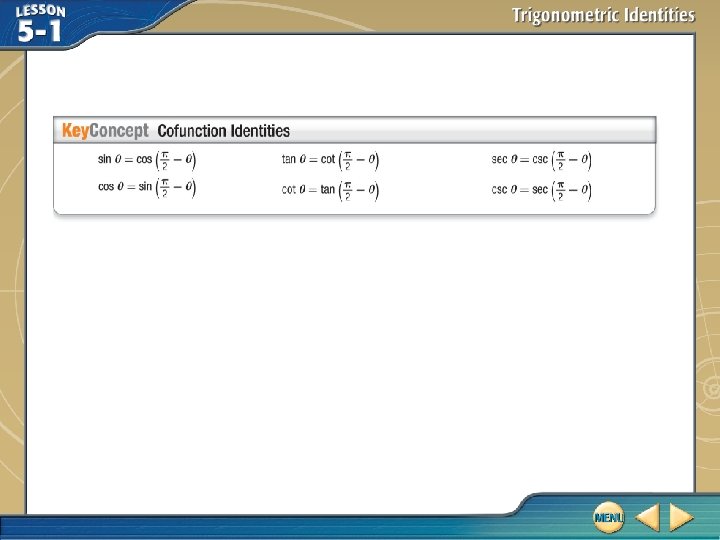
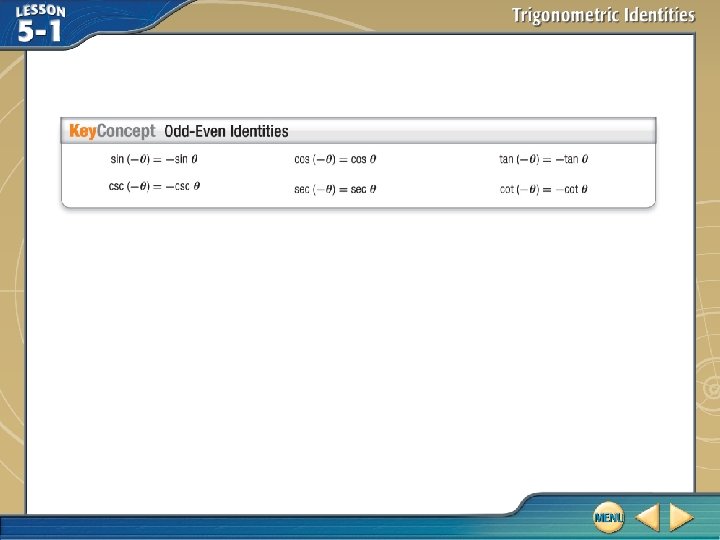
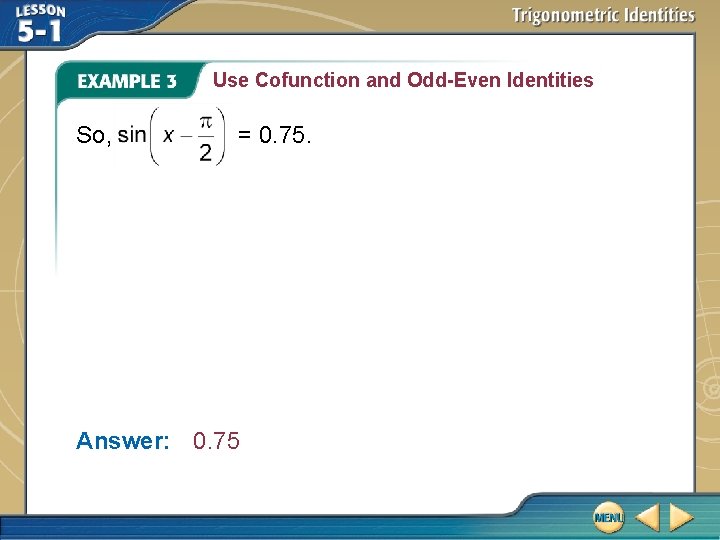
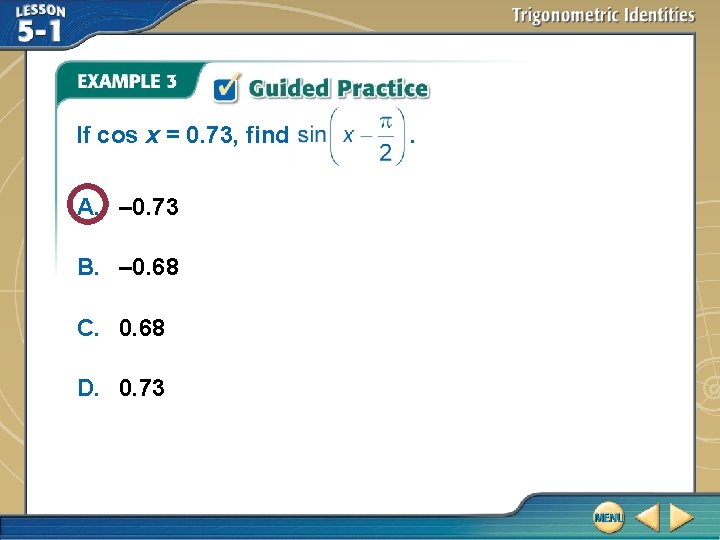
Use Cofunction and Odd-Even Identities If cos x = – 0. 75, find Factor. Odd-Even Identity Cofunction Identity cos x = – 0. 75 Simplify.

Use Cofunction and Odd-Even Identities So, = 0. 75. Answer: 0. 75

If cos x = 0. 73, find A. – 0. 73 B. – 0. 68 C. 0. 68 D. 0. 73 .

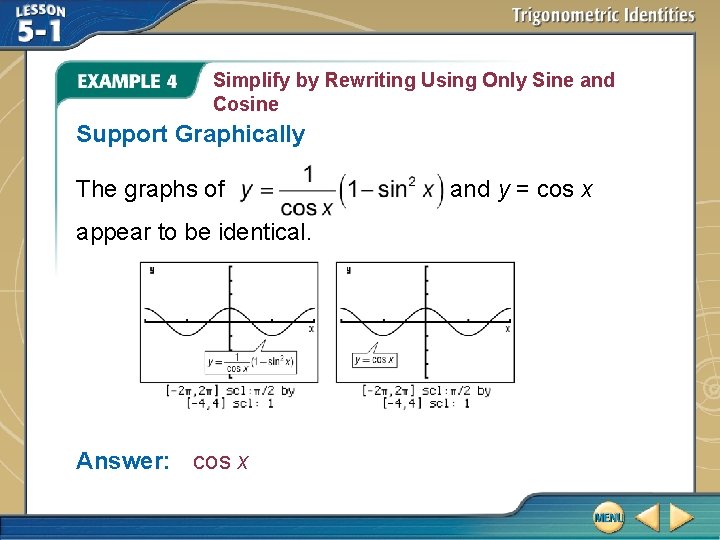
Simplify by Rewriting Using Only Sine and Cosine Simplify . Solve Algebraically Pythagorean Identity Multiply. Simplify. So, = cos x.

Simplify by Rewriting Using Only Sine and Cosine Support Graphically The graphs of appear to be identical. Answer: cos x and y = cos x

Simplify csc x – cos x cot x. A. cot x B. tan x C. cos x D. sin x

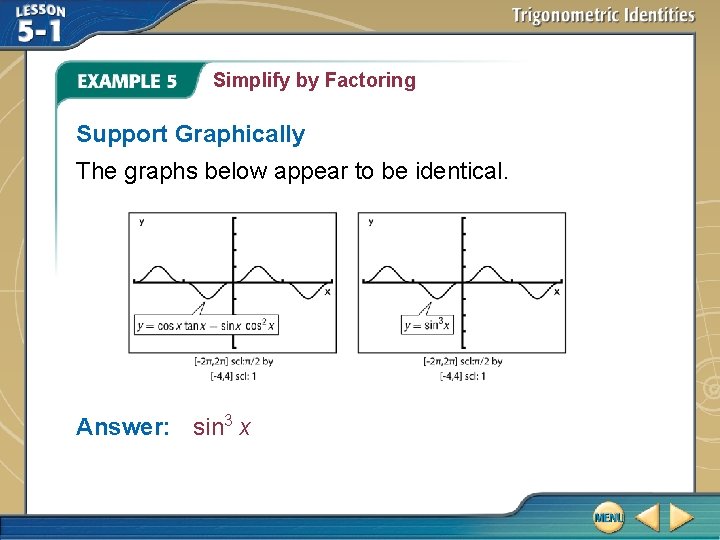
Simplify by Factoring Simplify cos x tan x – sin x cos 2 x. Solve Algebraically cos x tan x – sin x cos 2 x Original expression Quotient Identity Multiply. Factor. Pythagorean Identity = sin 3 x Simplify. So, cos x tan x – sin x cos 2 x = sin 3 x.

Simplify by Factoring Support Graphically The graphs below appear to be identical. Answer: sin 3 x

Simplify cos 2 x sin x – cos(90° – x). A. –sin 3 x B. sin 3 x C. cos 2 x – 1 D. sin x cos x

Simplify by Combining Fractions Simplify . Common denominator Multiply. Add the numerators. Simplify. Pythagorean Identity

Simplify by Combining Fractions Reciprocal Identity Reciprocal and Quotient Identities Divide out common factor. Reciprocal Identity – 2 csc 2 x. Answer: – 2 sec 2 x

Simplify A. cos x B. 2 + 2 cos x C. 2 sin x D. 2 csc x .

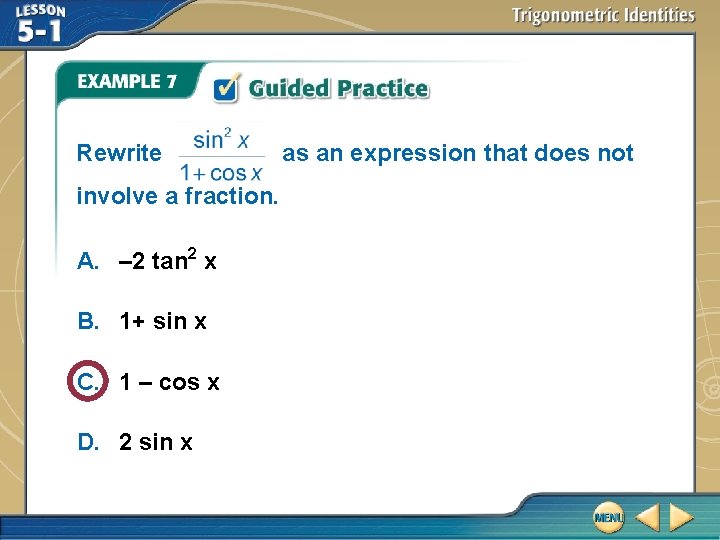
Rewrite to Eliminate Fractions Rewrite as an expression that does not involve a fraction. Pythagorean Identity Reciprocal Identity Quotient Identity

Rewrite to Eliminate Fractions So, = tan 2 x. Answer: tan 2 x

Rewrite involve a fraction. A. – 2 tan 2 x B. 1+ sin x C. 1 – cos x D. 2 sin x as an expression that does not

LESSON 5– 1 Trigonometric Identities