LESSON 5 2 Verifying Trigonometric Identities FiveMinute Check





































- Slides: 39

LESSON 5– 2 Verifying Trigonometric Identities

Five-Minute Check (over Lesson 5 -1) TEKS Then/Now New Vocabulary Example 1: Verify a Trigonometric Identity Example 2: Verify a Trigonometric Identity by Combining Fractions Example 3: Verify a Trigonometric Identity by Multiplying Example 4: Verify a Trigonometric Identity by Factoring Example 5: Verify an Identity by Working Each Side Separately Concept Summary: Strategies for Verifying Trigonometric Identities Example 6: Determine Whether an Equation is an Identity

Over Lesson 5 -1 Find the value of the expression using the given information. If tan θ = A. B. C. D. , find cot θ.

Over Lesson 5 -1 Find the value of the expression using the given information. If sin θ = A. B. C. D. and cos θ = , find tan θ.

Over Lesson 5 -1 Find the value of the expression using the given information. If csc θ = 3 and cos θ < 0, find cos θ and tan θ. A. B. C.

Over Lesson 5 -1 Simplify csc x – csc x cos 2 x. A. sin x B. cos x C. csc x(1 + sin x) D. 1 – cos x

Over Lesson 5 -1 If sin θ = 0. 59, find A. − 0. 81 B. − 0. 59 C. 0. 59 D. 0. 81 .

Targeted TEKS P. 5(M) Use trigonometric identities such as reciprocal, quotient, Pythagorean, cofunctions, even/odd, and sum and difference identities for cosine and sine to simplify trigonometric expressions. Mathematical Processes P. 1(C), P. 1(F)

You simplified trigonometric expressions. (Lesson 5 -1) • Verify trigonometric identities. • Determine whether equations are identities.

• verify an identity

Verify a Trigonometric Identity Verify that . The left-hand side of this identity is more complicated, so transform that expression into the on the right. Pythagorean Identity Reciprocal Identity Simplify.

Verify a Trigonometric Identity Answer:

Verify that 2 – cos 2 x = 1 + sin 2 x. A. 2 – cos 2 x = –(sin 2 x + 1) + 2 = 1 + sin 2 x B. 2 – cos 2 x = 2 – (sin 2 x + 1) = 1 + sin 2 x C. 2 – cos 2 x = 2 – (1 + sin 2 x) + 2 = 1 + sin 2 x D. 2 – cos 2 x = 2 – (1 – sin 2 x) = 1 + sin 2 x

Verify a Trigonometric Identity by Combining Fractions Verify that . The right-hand side of the identity is more complicated, so start there, rewriting each fraction using the common denominator 1 – cos 2 x. Start with the right hand side of the identity. Common denominator Distributive Property

Verify a Trigonometric Identity by Combining Fractions Simplify. Divide out the common factor of sin x. Simplify. Quotient Identity

Verify a Trigonometric Identity by Combining Fractions Answer:

Verify that A. B. C. D. .

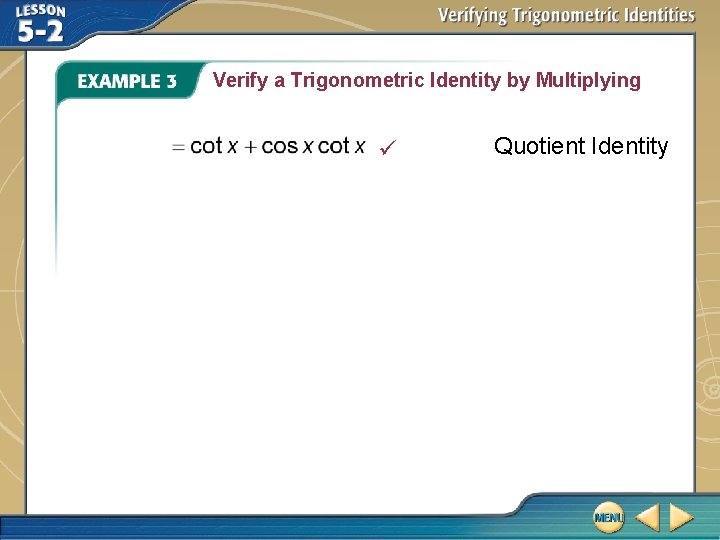
Verify a Trigonometric Identity by Multiplying Verify that . Because the left-hand side of this identity involves a fraction, it is slightly more complicated than the right side. So, start with the left side. Multiply the numerator and denominator by the conjugate of sec x – 1, which is sec x + 1. Multiply.

Verify a Trigonometric Identity by Multiplying Pythagorean Identity Quotient Identity Multiply by the reciprocal of the denominator. Divide out the common factor of sin x.

Verify a Trigonometric Identity by Multiplying Distributive Property Rewrite the fraction as the sum of two fractions; Reciprocal Identity. Divide out the common factor of cos x.

Verify a Trigonometric Identity by Multiplying Quotient Identity

Verify a Trigonometric Identity by Multiplying Answer:

Verify that A. B. C. D. .

Verify a Trigonometric Identity by Factoring Verify that cos x sec 2 x tan x – cos x tan 3 x = sin x. cos x sec x tan x – cos x tan x = cos x tan x (sec 2 x – tan 2 x) Start with the lefthand side of the identity. Factor. = cos x tan x (1) Pythagorean Identity = Quotient Identity = sin x Divide out the common factor of cos x. 2 3

Verify a Trigonometric Identity by Factoring Answer: cos x sec 2 x tan x – cos x tan 3 x = cos x tan x (sec 2 x – tan 2 x) = cos x tan x (1) = = sin x

Verify that csc x – cos x cot x + cot x = sin x. A. B. C. D.

Verify an Identity by Working Each Side Separately Verify that cot 3 x + cot x = cos x csc 3 x. Both sides look complicated, but there is a clear first step for the expression on the left. So, start with the expression on the left. cot 3 x + cot x = cot x (cot 2 x + 1) Start with the left-hand side of the identity. Factor.

Verify an Identity by Working Each Side Separately cot x (cot 2 x + 1) = cot x (csc 2 x) Pythagorean Identity Reciprocal and Quotient Identities Multiply = cos x csc 3 x Reciprocal Identity

Verify an Identity by Working Each Side Separately

Verify that tan 2 x – sin 2 x = sin 2 x tan 2 x. A. B. C. D.


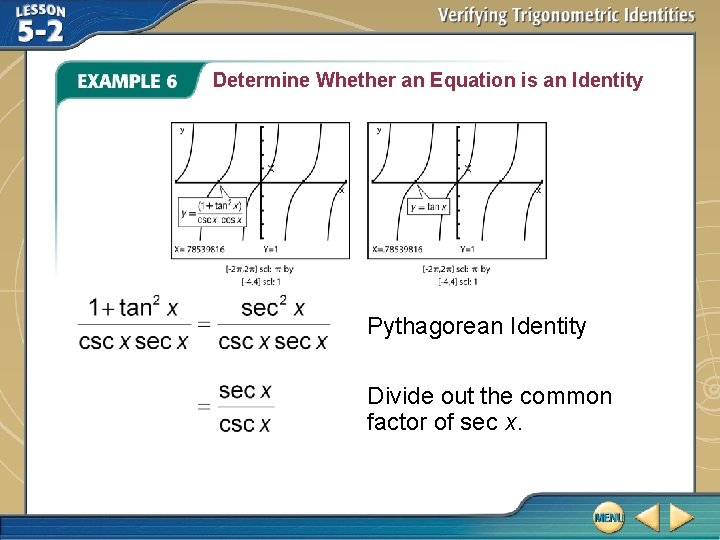
Determine Whether an Equation is an Identity A. Use a graphing calculator to test whether is an identity. If it appears to be an identity, verify it. If not, find an x-value for which both sides are defined but not equal. The equation appears to be an identity because the graphs of the related functions over [– 2π, 2π] scl: π by [– 1, 3] scl: 1 coincide. Verify this algebraically.

Determine Whether an Equation is an Identity Pythagorean Identity Divide out the common factor of sec x.

Determine Whether an Equation is an Identity Reciprocal Identities Simplify. Quotient Identity Answer:

Determine Whether an Equation is an Identity B. Use a graphing calculator to test whether is an identity. If it appears to be an identity, verify it. If not, find an x-value for which both sides are defined but not equal.

Determine Whether an Equation is an Identity The graphs of the related functions do not coincide for all values of x for which the both functions are defined. When , Y 1 ≈ 1. 43 but Y 2 ≈ – 0. 5. The equation is not an identity.

Determine Whether an Equation is an Identity Answer: When , Y 1 ≈ 1. 43 but Y 2 = – 0. 5. The equation is not an identity.

Use a graphing calculator to test whether is an identity. If it appears to be an identity, verify it. If not, find a value for which both sides are defined but not equal. A. The equation appears to be an identity because the graphs of the related functions over [– 2π, 2π] scl: π by [– 3, 3] scl: 1 coincide. B. When , Y 1 ≈ 0. 71 but Y 2 ≈ 0. 29. The equation is not an identity.

LESSON 5– 2 Verifying Trigonometric Identities