5 Trigonometric Identities 5 1 Fundamental Identities Using

5. 1 Fundamental Identities ▪ Using the Fundamental Identities

Fundamental Identities An identity is an equation that is satisfied by every value in

Fundamental Identities We saw all of the identities in this section in chapter 2.

P. 193, #1, 2, 5 USING NEGATIVE ANGLE IDENTITIES 1. If tan θ =

Reciprocal Identities We can switch between reciprocal functions by moving the function from top

P. 195, #46, 63 USING RECIPROCAL IDENTITIES Write in terms of sine and cosine

Quotient Identities For all angles θ for which the denominators are not zero, the

Pythagorean Identities For all angles θ for which the function values are defined, the

Deriving the Pythagorean Identities r=1 θ

Alternate forms of the Pythagorean Identities

Example 1 If FINDING TRIGONOMETRIC FUNCTION VALUES GIVEN ONE VALUE AND THE QUADRANT and

P. 194, #13 13. If FINDING TRIGONOMETRIC FUNCTION VALUES GIVEN ONE VALUE AND THE

P. 194, #37 37. If functions of θ. FINDING TRIGONOMETRIC FUNCTION VALUES GIVEN ONE

P. 195, #60, 62 WRITING EXPRESSIONS IN TERMS OF SIN AND COS Write each

P. 195, #76 WRITING EXPRESSIONS IN TERMS OF SIN AND COS Write each expression

P. 195, #80 PYTHAGOREAN SUBSTITUTION Write each expression in terms of sine and cosine,

Example 3 Write REWRITING AN EXPRESSION IN TERMS OF SINE AND COSINE in terms

Caution When working with trigonometric expressions and identities, be sure to write the argument

P. 195, #74 USING COMMON DENOMINATORS Write each expression in terms of sine and

P. 195, #69 SPLITTING ONE FRACTION INTO TWO FRACTIONS Write each expression in terms

Slides: 24

Download presentation

5 Trigonometric Identities

5. 1 Fundamental Identities ▪ Using the Fundamental Identities

Fundamental Identities An identity is an equation that is satisfied by every value in the domain of its variable.

Fundamental Identities We saw all of the identities in this section in chapter 2. Although you will be given an identity sheet to use on all upcoming tests, these identities will NOT be on that sheet, so you should MEMORIZE THEM!

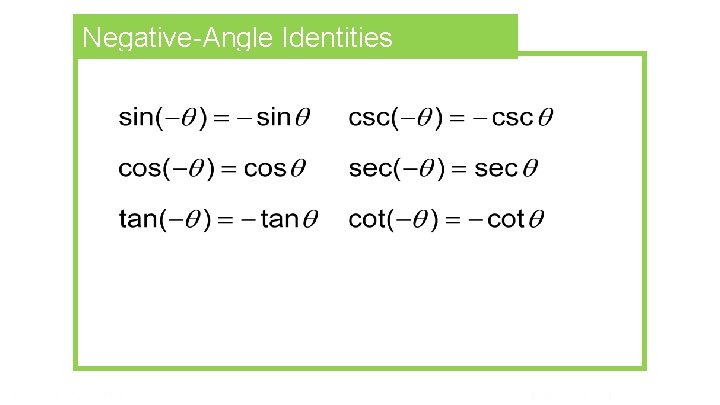
Negative-Angle Identities

The Negative Angle Identities

P. 193, #1, 2, 5 USING NEGATIVE ANGLE IDENTITIES 1. If tan θ = 2. 6, then tan(- θ) = 2. If cos θ = -0. 65, then cos(- θ) = 5. If sin θ = 2/3, then –sin(- θ) =

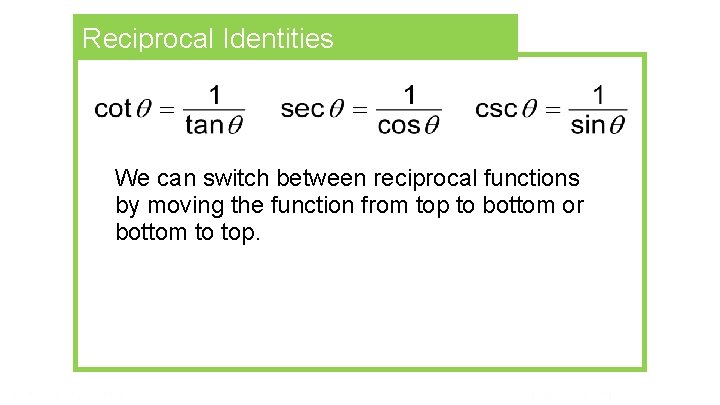
Reciprocal Identities We can switch between reciprocal functions by moving the function from top to bottom or bottom to top.

P. 195, #46, 63 USING RECIPROCAL IDENTITIES Write in terms of sine and cosine and simplify so that no quotients appear. 46. 63. cos θ csc θ

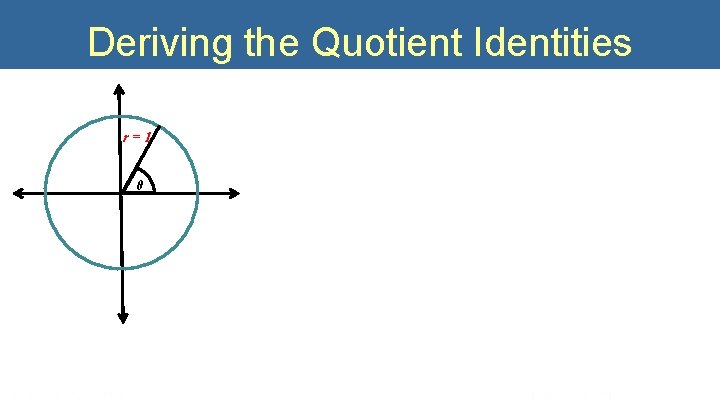
Quotient Identities For all angles θ for which the denominators are not zero, the following identities hold.

Deriving the Quotient Identities r=1 θ

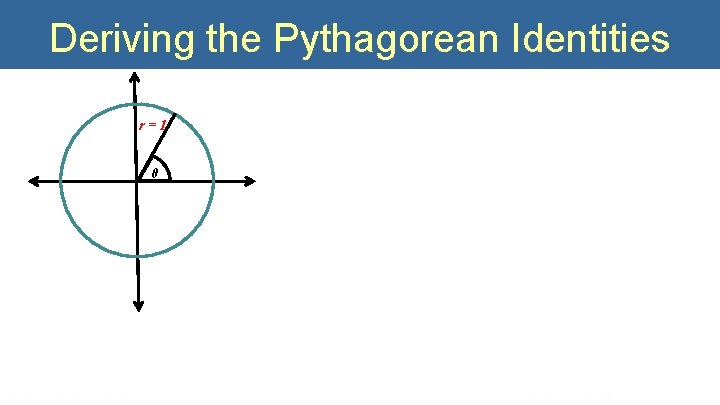
Pythagorean Identities For all angles θ for which the function values are defined, the following identities hold.

Deriving the Pythagorean Identities r=1 θ

Alternate forms of the Pythagorean Identities

Example 1 If FINDING TRIGONOMETRIC FUNCTION VALUES GIVEN ONE VALUE AND THE QUADRANT and θ is in quadrant II, find each function value. (a) sec θ (b) sin θ (c) cot(– θ)

P. 194, #13 13. If FINDING TRIGONOMETRIC FUNCTION VALUES GIVEN ONE VALUE AND THE QUADRANT (the easy way) and cosθ > 0, find sinθ.

P. 194, #37 37. If functions of θ. FINDING TRIGONOMETRIC FUNCTION VALUES GIVEN ONE VALUE AND THE QUADRANT (the easy way) and sin θ < 0, find the remaining five trig

P. 195, #60, 62 WRITING EXPRESSIONS IN TERMS OF SIN AND COS Write each expression in terms of sine and cosine, and simplify so that no quotients appear in the final expression and all functions are of θ only. 60. tanθ cos θ 62. csc θ cos θ tan θ

P. 195, #76 WRITING EXPRESSIONS IN TERMS OF SIN AND COS Write each expression in terms of sine and cosine, and simplify so that no quotients appear in the final expression and all functions are of θ only. 76. (sin θ - cos θ)(csc θ + sec θ)

P. 195, #80 PYTHAGOREAN SUBSTITUTION Write each expression in terms of sine and cosine, and simplify so that no quotients appear in the final expression and all functions are of θ only. 80.

Example 3 Write REWRITING AN EXPRESSION IN TERMS OF SINE AND COSINE in terms of sin θ and cos θ, and then simplify the expression so that no quotients appear.

Caution When working with trigonometric expressions and identities, be sure to write the argument of the function. For example, we would not write An argument such as θ is necessary in this identity.

P. 195, #74 USING COMMON DENOMINATORS Write each expression in terms of sine and cosine, and simplify so that no quotients appear in the final expression and all functions are of θ only. 74. csc θ - sin θ

P. 195, #69 SPLITTING ONE FRACTION INTO TWO FRACTIONS Write each expression in terms of sine and cosine, and simplify so that no quotients appear in the final expression and all functions are of θ only. 69.