A Trigonometric Ratios of an Angle Trigonometric Ratios

A. Trigonometric Ratios of an Angle

Trigonometric Ratios of Right Triangle n n n Create three right triangles with right angle length 3 cm and 4 cm, respectively name ABC, 6 cm and 8 cm, name DEF, and 9 cm and 12 cm, name PQR. R F C A B D E P Q Using Pythagorean theorem, you should be able to calculate length of side AC, DF, and PR (hypotenuse) of 15 cm, 10 cm, and 15 cm, respectively. Further, compare A, D, and P measure. In fact, A=B=P. Trigonometric ratios for A in right triangle ABC is defined as follows. a. BC/AC is called sine A abbreviated by sin A b. AB/AC is called cosine A abbreviated by cos A c. BC/AB is called tangent A abbreviated by tan A d. AB/BC is called cotangent A abbrevaited by cot A e. AC/AB is called secant A abbreviated by sec A f. AC/BC is called cosecant A abbreviated by csc A

n n At whole, trigonometric ratios values of angle in the three triangles are as follows. sin = 3/5 d. cot alpha =4/3 cos alpha = 4/5 e. sec alpha =5/4 tan alpha = 3/4 f. csc alpha =4/3 Of those ratios, following relationship are obtained.

Trigonometric Ratios on Coordinates System n n Observe beside figure. Beside figure is a circle with centre O(0, 0) and radius r. Angle is angle between positive X -axis and line OP. Line OP can be rotated that measure of angle ranges between Coordinates of P is P(x, y). Length of circle radius is r so that

n Trigonometric Ratios for Angle are definited as follows if angle = 0 o, then the point coordinates of P(x, y) is P(r, 0). It means that as follows n n n Sin α = y/r Cot α = x/y tan α = y/x cot α = x/y sec α = r/x csc α = r/y

If angle α = 0 o, the point coordinate of P(x, y) is P(r, 0). It means that as follows. sin 0 o = y/r = 0; cos 0 o = x/r = r/r = 1; tan 0 o = y/x = 0/r = 0 if angle α = 90 o, then coordinate of point P(x, y) is P(0, r). It means that as follows. sin 90 o = y/x = r/r = 1; cos 90 o = x/r = 0/r; tan 90 o = y/x = r/0 (undefined).

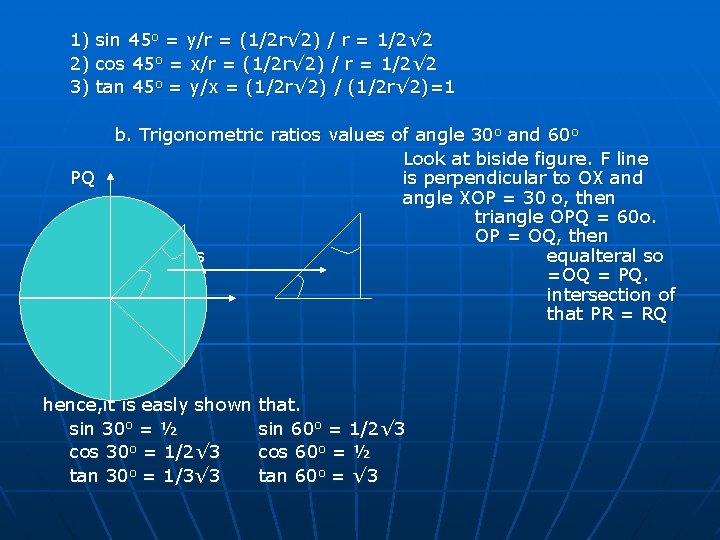
Extraordianary Angle Trigonometric Ratios n There are some angles that is trigonometric ratios value can be determined without trigonometric table or calculator aid, for examples 0 o, 30 o, 45 o, 60 o, and 90 o. Those angles are caled extraordianary angles or special angles, which its trigonometric ratio value can be determined among orthers, by using trigonometric ratios definition on the circle at centre point o(0, 0) and radius r. Subject on 0 o and 90 o have been studied before. a. Trigonometric Ratios Value of Angle 45 o. Look out at beside figure. It seems that XOY is right angle. Hence, if angle XOP = 45 o, then angle YOP = 45 o.

1) sin 45 o = y/r = (1/2 r√ 2) / r = 1/2√ 2 2) cos 45 o = x/r = (1/2 r√ 2) / r = 1/2√ 2 3) tan 45 o = y/x = (1/2 r√ 2) / (1/2 r√ 2)=1 b. Trigonometric ratios values of angle 30 o and 60 o Look at biside figure. F line PQ is perpendicular to OX and angle XOP = 30 o, then triangle OPQ = 60 o. Because OP = OQ, then triangle OPQ is equalteral so that length OP =OQ = PQ. Point R is intersection of PQ and OX so that PR = RQ = 1/2 r. hence, it is easly shown sin 30 o = ½ cos 30 o = 1/2√ 3 tan 30 o = 1/3√ 3 that. sin 60 o = 1/2√ 3 cos 60 o = ½ tan 60 o = √ 3

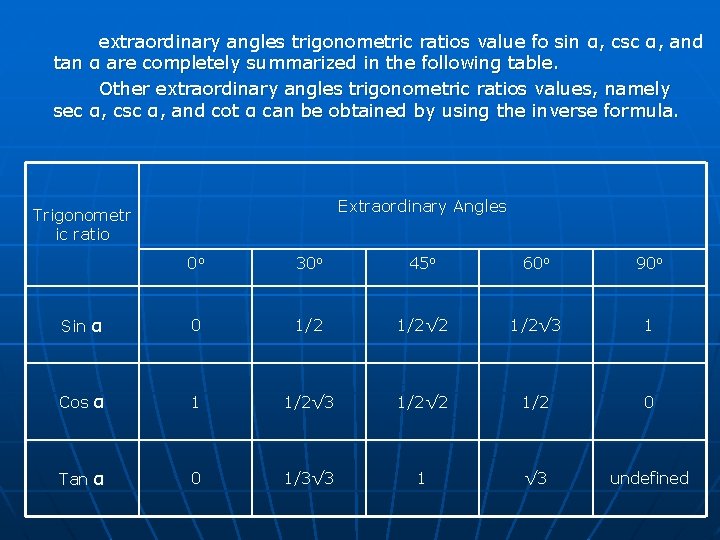
extraordinary angles trigonometric ratios value fo sin α, csc α, and tan α are completely summarized in the following table. Other extraordinary angles trigonometric ratios values, namely sec α, csc α, and cot α can be obtained by using the inverse formula. Extraordinary Angles Trigonometr ic ratio 0 o 30 o 45 o 60 o 90 o Sin α 0 1/2√ 2 1/2√ 3 1 Cos α 1 1/2√ 3 1/2√ 2 1/2 0 Tan α 0 1/3√ 3 1 √ 3 undefined

II I Coordinate pivots at beside figure divides coordinate plane into for areas, which furhtermore, is called quardant. Thus, angle quantity can be classified into four quadrants, III IV namely as follows. a. quadrant I : 0 o < α ≤ 90 o b. quadrant II : 90 o < α ≤ 180 o c. quadrant III: 180 o < α ≤ 270 o d. quadrant IV: 270 o < α ≤ 360 o If α is at quadrant I, then x and y are positve. sin α = y/r > 0 cos α = x/r > 0 tan α = y/x > 0

Determined Uknow Right-Angled Triangle Component Trigonometric value can be used to determined side length of right-angled triangle if of its acute angle is know. In addidion, we caan also determined the quantity of two acute angles if at least there are two sides known.

Formula of Related Angled Trigonometric Ratios Related angle is angle pairs that have any relation so that trigonometric ratios of its angles fulfill certain formula. Some related angles trigonometic ratios formula will b explainned in the following section. a. Angle α with 90 o – α Point P’(x’, y’) is a reflection result of point P 9 x, y) towards line y = x so that x’ = y and y’ = x. Therefore, coordinate of point P’(x’, y’) is p’(y, x). <xop = α <xop = 90 o – α OP = OP’= r Considering coordinate of point P’(x’. y’) =n. P’(y, x), then for angle 90 o – α the following apply. sin (90 o – α) = y’/OP’ tan (90 o – α) = y’/x’ = x/r = cos α = x/y = cot α cos (90 o – α) = x’/OP’ = y/r = sin α Determined the values cot, sec, and csc of angle 90 o – α.

b. Angle α with 180 o – α Line segment OP’ on beside figure is shadow of line segment OP if ppoint P is resflected aggaint Y-axis o that the shadow is P’. Because o that reflections, the following relations accur. a. <XOP = α; <XOP’ = (180 o – α) b. r’ = r’, x’ = -x; y’ = y. thus, coordinate of point P’(x’, y’) = P’(-x, y). brcause in coordinate P’(x’, y’) has a relation P’(x’, y’) = (x, y), for angle (180 o – α) the following trigonometric ratios is obtained. a. sin (180 o – α) = y/r = sin α b. cos (180 o – α) = -x/r = -cos α c. tan (180 o – α) = y/-x = -tan α determine value cot, sec, and csc of angle 180 o – α.

c. angle α with (180 o + α) Point P” in the following figure is the shadow from point P after passing twice reflection respectively, namely against Y-axis is continued to X-axis. Thus, line segment OP is also shadow of line segment OP through twice reflection in similar way that is against Y-axis is continued to X-axis. Because of the reflection , the following relation is obtained. a. <XOP = α; <XOP” = (180 o = α) b. r” = r, x” = -x; y” = -y therefore, P”(x”, y”) = P(-x, -y). As a consequence of the relation, for angle (180 o + α), the following trigonometric ratios is found. a. sin (180 o + α) = -y/r = -sin α b. cos (180 o + α) = -x/r = -cos α c. tan (180 o + α) = -y/-x = y/x = tan α Determine the values cot, sec, and csc of angle 180 o + α.

d. angle α with (360 o – α) Point P is reflected against X-axis so that image is point P’. Thus, the length of line segment OP equals to line segment OP. Due to the reflection, the following relation is obtained. a. <OXP = α; <XOP’ =m(360 o - α ) = - α b. r’ = r; x’ = x; y’ = -y Therefore, P’(x’, y’) = P(x, -y) As a conequence of this relation, trigonometric ratios for (360 o – α) angle is as follows. a. sin (360 o - α ) = -y/r = -sin α b. cos (360 o - α ) = x/r = cos α c. tan (360+ - α ) = -y/x = -tan α Determine cot, sec, and csc value for angle 360 o - α. Angle (360 o - α ) may be also viewed as angle - α so that trigonometric ratios valu for angle - α is as follows. sin (- α ) = -sin α cot (- α ) = -cot α cos (i α ) = cos α sec (- α ) = sec α tan (- α ) = -tan α csc (- α ) = - csc α

e. angle α with (k x 360 o + α) if line OP on beside figure is rotated in one full rotation as much as k times and P’(x’, y’) is rotation resulted from P(x, y), then P’(x’, y’) will be very coincide with P(x. y) so that x’ = x, y’ = y is obtained, and length OP’ = length OP = r. By paying attention to pervious result, that is tan (180+ α) = tan α and α (180+ α) = cot v then if k is integer, applies as follows. sin (k x 360 o + α) = sin α cos (k x 360 o + α) = cos α tan (k x 180 o + α) = tan α sec (k x 360 o + α) = sec α csc (k x 360 o + α) = csc α cot (k x 180 o + α) = cot α