CLASS X SUB MATHEMATICS TOPIC INTRODUCTION TO TRIGONOMETRY

CLASS – X SUB. - MATHEMATICS TOPIC- INTRODUCTION TO TRIGONOMETRY

CONCEPT OF RATIO, CONCEPT OF SIMILARITY AND BIRTH OF A RIGHT ANGLED TRIANGLES https: //youtu. be/t. D 0 MXm_UDvk

A 8 cm D B 12 cm A B C 9 cm F 6 cm C

BIRTH OF A RIGHT ANGLED TRIANGLE Poem follows in the next slide: ART INTEGRATION

A triangular love story Once upon a time, in a distant mystic land, a triangle was born, drawn with a stick on some sand. Many had muttered, “She doesn’t seem all that bright; She’d never fit in, her angle’s too right. ” She wondered if she could serve a greater good, offer to the world something no triangle could. She worried if her gift, she would ever really find, Or would she just leave, forgotten from everyone's mind. She glanced at herself in the mirror, day after day, knowing there was something, she had yet to say. She pondered for long and decided to leave. Leave her lonely village, for a faraway town. Perhaps just to visit, perhaps to settle down. There, a beauty contest, the most famous of them all, wanted all triangles: short, stocky and tall. She wanted to know where she really stood; everyone coaxed her “you should, oh you should”.

She told herself, there was nothing to beware, “After all, they’re gonna measure you fair and square. ” Measure they did, with their cold metallic tools, commenting, oh the ignorant fools, “Isn't her base just a little too wide? Is her height really on the right side? ” She was broken. Almost ready to cry. Until one of them gasped and said, look over here, look what I found. The square of her base and the square of her height, add exactly to the square of the side that's tilted aslight. She was confused, baffled, by all of the noise, “That’s how I was born, I had not a choice. ” – BIRTH OF A RIGHT “She’s just right, just perfect”, they said. She became divine, though this was all in their head. They put her on the covers, signed her for promotions. So smitten were they, they even named her proportions. “Her height by hypotenuse will be called sine, Her base by hypotenuse shall be cosine, her height by her base is to be named tan”. And that's how my children, this story began.

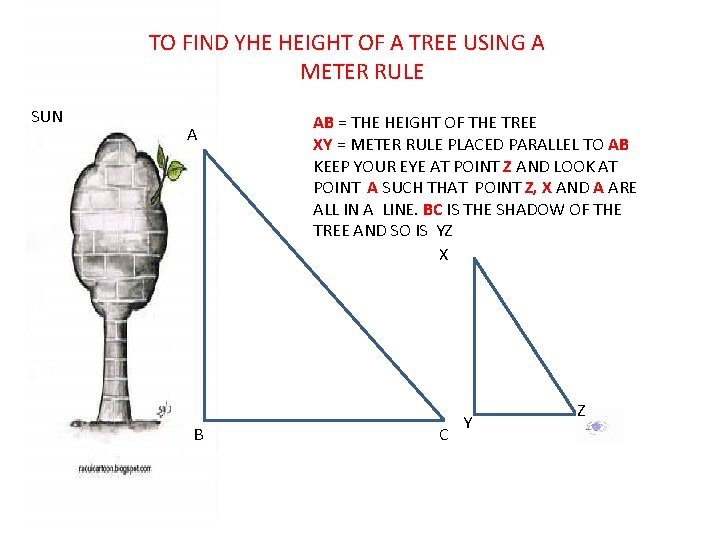
TO FIND YHE HEIGHT OF A TREE USING A METER RULE SUN A B AB = THE HEIGHT OF THE TREE XY = METER RULE PLACED PARALLEL TO AB KEEP YOUR EYE AT POINT Z AND LOOK AT POINT A SUCH THAT POINT Z, X AND A ARE ALL IN A LINE. BC IS THE SHADOW OF THE TREE AND SO IS YZ X C Y Z

THERE IS PERHAPS NOTHING WHICH SO OCCUPIES THE MIDDLE POSITION OF MATHEMATICS AS TRIGONOMETRY J. F HERBART

LEARNING OBJECTIVES § Identify the hypotenuse, adjacent sides and opposite sides of an acute angle in a right angled triangle §Determine the six trigonometric ratios for a given angle in a right angled triangle. §Find the exact trigonometric function values for angles that measure 00, 300, 450 , 600 , 900 § Determine the relationship between the trigonometric ratios of complementary angles §Able to prove trigonometric identities and use it to prove other useful trigonometric identities.

INTRODUCTION TO TRIGONOMETRY DERIVED FROM A GREEK WORD “TRI” MEANS THREE, “GONIA” MEANS ANGLE AND “METRON” MEANS MEASURE. THUS THE LITERAL MEANING OF TRIGONOMETRY IS MESUREMENT IF THREE ANGLES AND SINCE A TRIANGLE HAS THREE ANGLES, THEREFORE, TROGONOMETRY MEANS MEASUREMENT OF TRIANGLES.

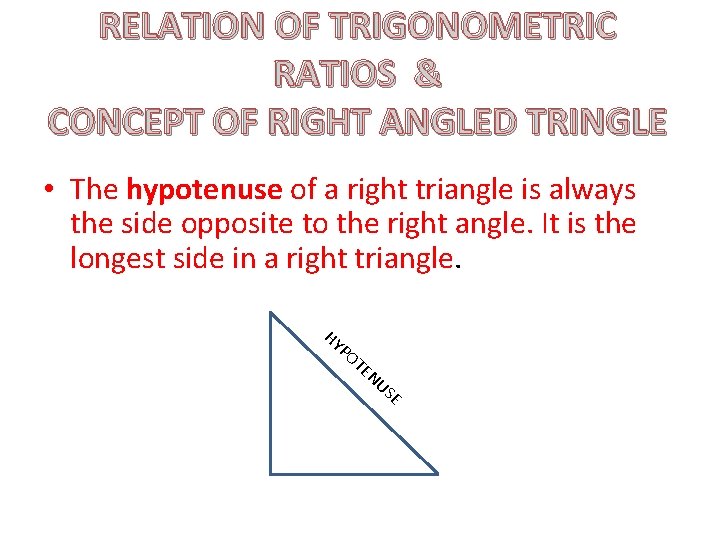
RELATION OF TRIGONOMETRIC RATIOS & CONCEPT OF RIGHT ANGLED TRINGLE • The hypotenuse of a right triangle is always the side opposite to the right angle. It is the longest side in a right triangle. HY PO TE NU SE

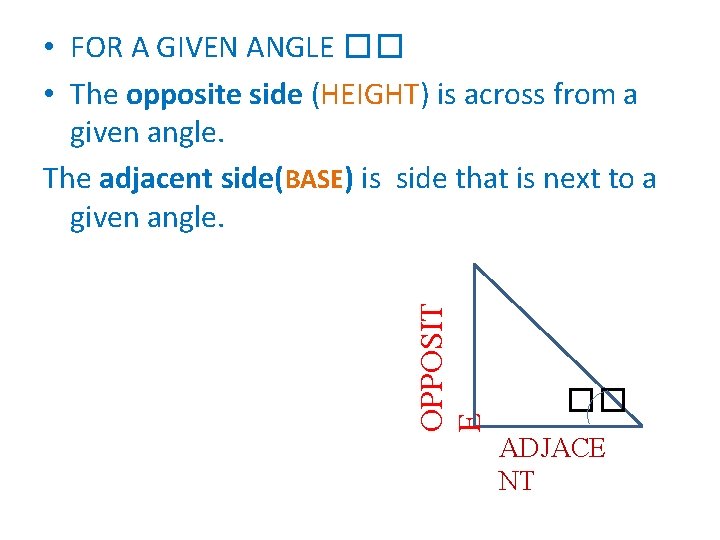
OPPOSIT E • FOR A GIVEN ANGLE �� • The opposite side (HEIGHT) is across from a given angle. The adjacent side(BASE) is side that is next to a given angle. �� ADJACE NT

IN TRIGONOMETRY THE RATIO OF SIDES OF A RIGHT ANGLED TRINGLES AND THEIR RELATIONS WITH ANGLES ARE DISCUSSED. THE RATIOS ARE CALLED TRIGONOMETRICAL RATIOS.

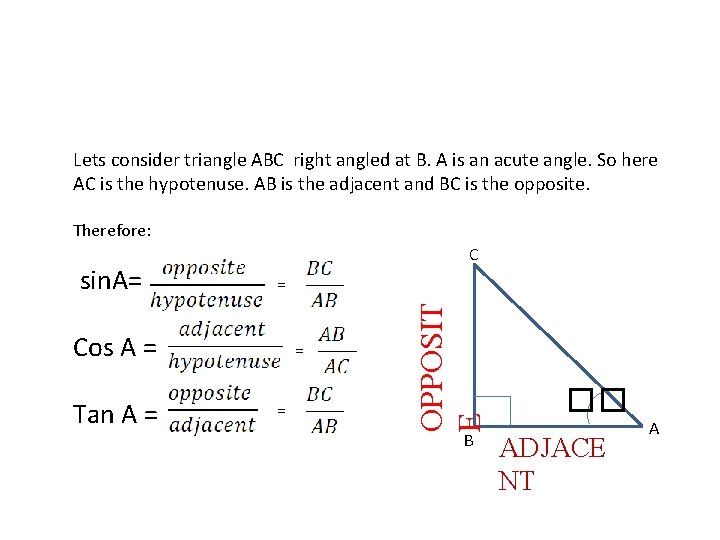
Lets consider triangle ABC right angled at B. A is an acute angle. So here AC is the hypotenuse. AB is the adjacent and BC is the opposite. Therefore: = Cos A = Tan A = = = OPPOSIT E sin. A= C B �� ADJACE NT A

WAY TO REMENBER T- RATIOS • SOH-CAH-TOA: an easy way to remember trig ratios • The word Soh – Cah - Toa helps us remember the definitions of sine, cosine, and tangent. Here's how it works: Silly Old Henry, Caught Albert Hugging Two Old Aunts Some Old Hags Can't Always Hide Their Old Age

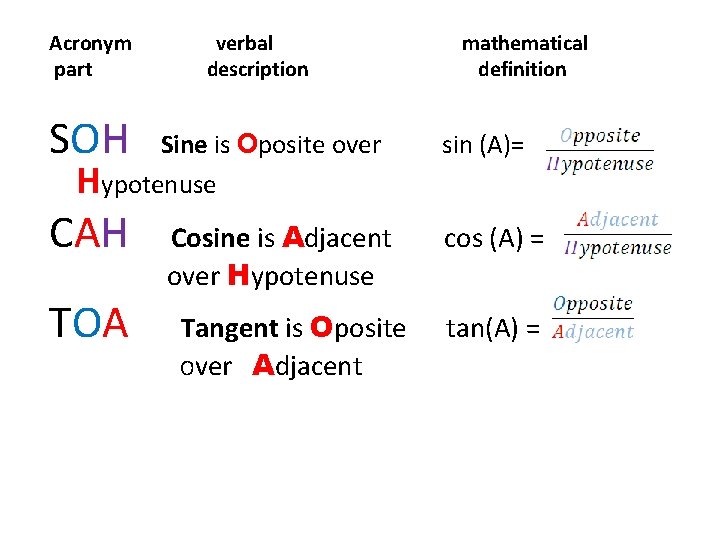
Acronym verbal mathematical part description definition SOH Sine is Oposite over sin (A)= Hypotenuse CAH Cosine is Adjacent cos (A) = over Hypotenuse TOA Tangent is Oposite tan(A) = Over Adjacent

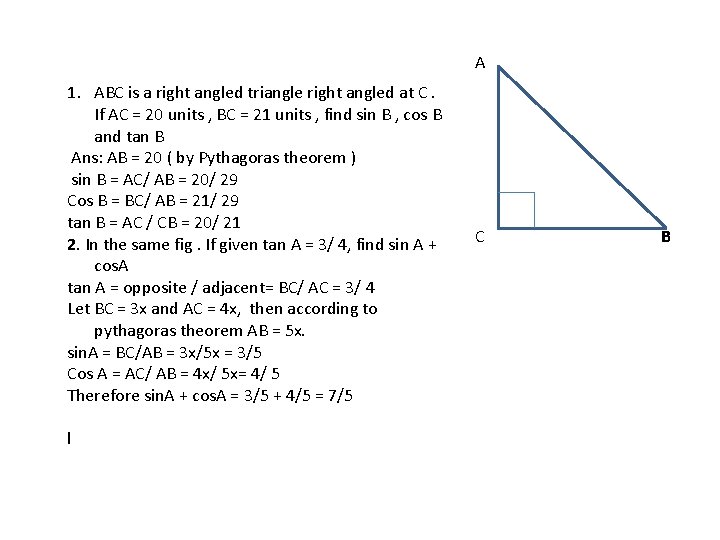
A 1. ABC is a right angled triangle right angled at C. If AC = 20 units , BC = 21 units , find sin B , cos B and tan B Ans: AB = 20 ( by Pythagoras theorem ) sin B = AC/ AB = 20/ 29 Cos B = BC/ AB = 21/ 29 tan B = AC / CB = 20/ 21 2. In the same fig. If given tan A = 3/ 4, find sin A + cos. A tan A = opposite / adjacent= BC/ AC = 3/ 4 Let BC = 3 x and AC = 4 x, then according to pythagoras theorem AB = 5 x. sin. A = BC/AB = 3 x/5 x = 3/5 Cos A = AC/ AB = 4 x/ 5 x= 4/ 5 Therefore sin. A + cos. A = 3/5 + 4/5 = 7/5 l C B

Reciprocal trigonometric ratios • Instead of we can have • Similarly instead of we can have • And instead of we can have

• The cosecant is the reciprocal of the sine. It is the ratio of the hypotenuse to the side opposite a given angle in a right triangle. • The secant is the reciprocal of the cosine. It is the ratio of the hypotenuse to the side adjacent to a given angle in a right triangle. • The cotangent is the reciprocal of the tangent. It is the ratio of the adjacent side to the opposite side in a right triangle. • cosec �� = = • sec �� = • tan �� = = =

1) In the given figure cot. A = 12/5 , find all other trigonometric ratio. Ans: cot A = adj / opposite = 12/5 B Let adjacent( AC) = 12 x and opposite( BC) = 5 x So hypotenuse AB = 13 x( using pythagoras) Sin A = opp/ hypo = BC/ AB = 5/ 13 Cos A = adj / hypo = AC/ AB = 12/ 13 tan. A = 5/ 12 Cosec A = hypo/ opp = AB / BC = 13/5 sec. A = hypo/ adj= 13/12 C 2. 4 tan�� = 5 , find Ans: 4 tan�� = 5 ⇒ tan �� = 5/4 = opp/ adj Opposite = 5 x and adjacent = 4 x Hypotenuse= = sin �� = opp/ hypo = 5/ Cos �� = adj / hypo = 4/ Sec �� = /4 sin �� + cos�� = 9/ ans: (9/ ) ∕( /4) = 9/4 A

TRIGONOMETRIC RATIOS OF SOME SPECIFIC ANGLES 00 , 300 , 450 , 600 and 900 From geometry we are already familiar with the construction of angles of these specific angles. We will only know the values of these trigonometric ratios for these angles and for 00 too(proof not required).

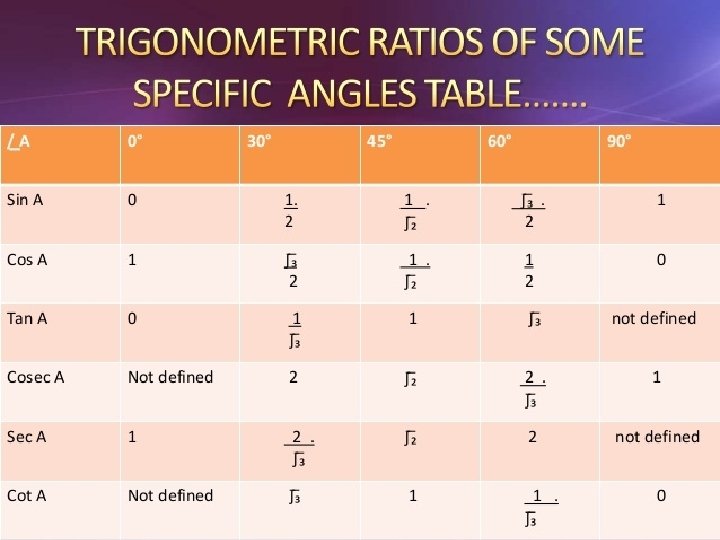
0 60 0 45 0 30 0 0 900 PALM TRICK METHOD

Q 1) Find the value of : tan 2300 + sin 2 900 + sec 2 450 Ans: ( )2 + (1)2 + )2 = (1/3)+1 +2= (1/3 )+3 = 10/3 2. I f A = 300 , show that sin ( 600 + A) – sin (600 –A) = sin A Ans: sin ( 600 + A) – sin (600 –A) = sin(60 + 30) – sin ( 60 – 30) = sin 900 - sin 300 = 1 - 1/2 = ½ = sin 300 = sin A (proved)

Trigonometric Ratio of complementary angles C ABC is a right angled triangle right angled at B. ∠B =900 ⇒ ∠A+∠C=900 So ∠C =900 - ∠A Sin ( 900 - ∠A) = opposite / hypotenuse = AB/ AC cos A= adjacent / hypotenuse = AB / AC ----(2) From (1) and (2) we get 0 – A) = cos. A 0 – A)= sin. A sin( 90 cos(90 0 – A) = cosec A In the same manner we can prove Sec (90 cosec (900 – A) = Sec A Tan(900 – A) = cot A cot(900 – A) = tan A A ---(1) B

TRIGONOMETRIC RATIOS OF COMPEMENTARY ANGLES • Sin(900 – A) = cos A • • • cos(900 – A)= sin. A Sec (900 – A) = cosec A cosec (900 – A) = Sec A Tan(900 – A) = cot A cot(900 – A) = tan A

TRICK TO REMEMBER : Wherever “ co” is not there with the trigonometric FUNCTION THEN ADD A “co” and whereever there is “ co” remove it. for example : when it is sine(900 – A) we get answer by adding co to it. so it is cosine A. Similarly : cosec (900 – A) = sec A is obtained by deleting “CO” From cosec which becomes sec

1) Evaluate : A ns: Cot A = tan(900 –A) 0 cot 250 = tan (900 – 250) = tan 65 = = 1 2) tan 2 A = cot (A - 180 ) where 2 A is acute angle, find the value of A ⇒ cot (900 – 2 A) = cot (A – 180 ) ⇒ (900 – 2 A) = (A – 180 ) ⇒ 3 A = 108 A= 360

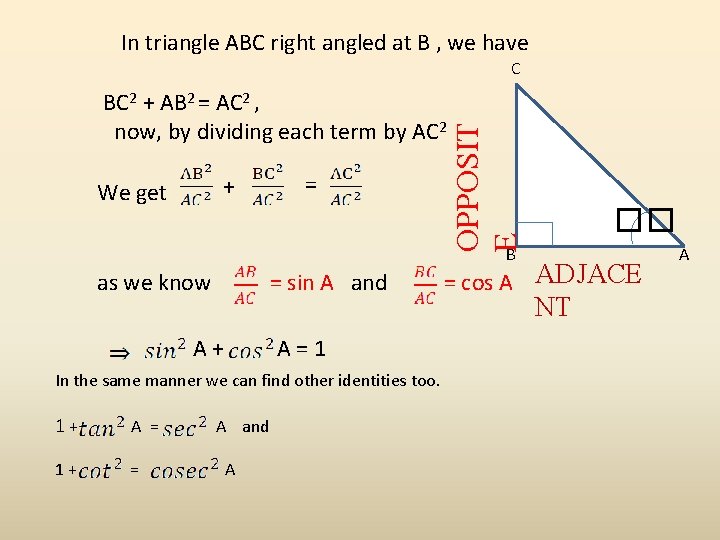
In triangle ABC right angled at B , we have C + = We get OPPOSIT E BC 2 + AB 2 = AC 2 , now, by dividing each term by AC 2 �� B as we know = sin A and A + = cos A ADJACE A = 1 In the same manner we can find other identities too. 1 + A = A and 1 + = A NT A

§While proving identities we start working with the LHS and simplify to get identically equal to the RHS. §Similarly, we can work only with the RHS and simplify it to the point where it's identically equal to the LHS. §You could simplify the LHS to reach an expression , and then, simplify the RHS to also reach the same expression, here you've proved both LHS and RHS are equal.

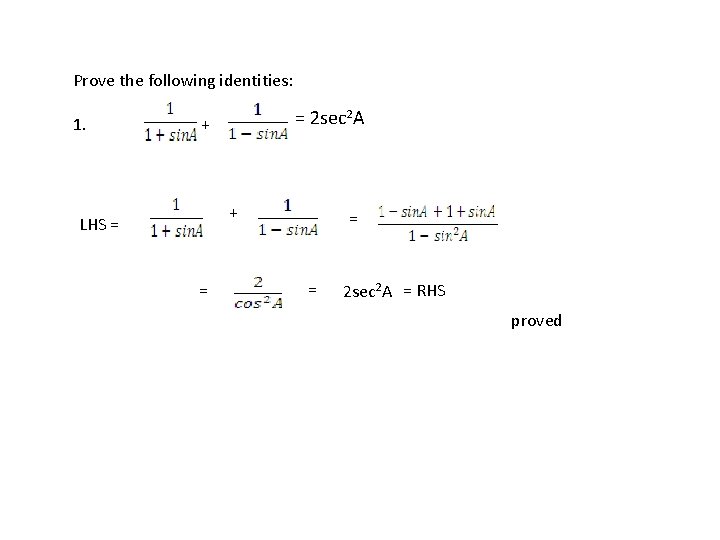
Prove the following identities: = 2 sec 2 A 1. + + = = = LHS = 2 sec 2 A = RHS proved

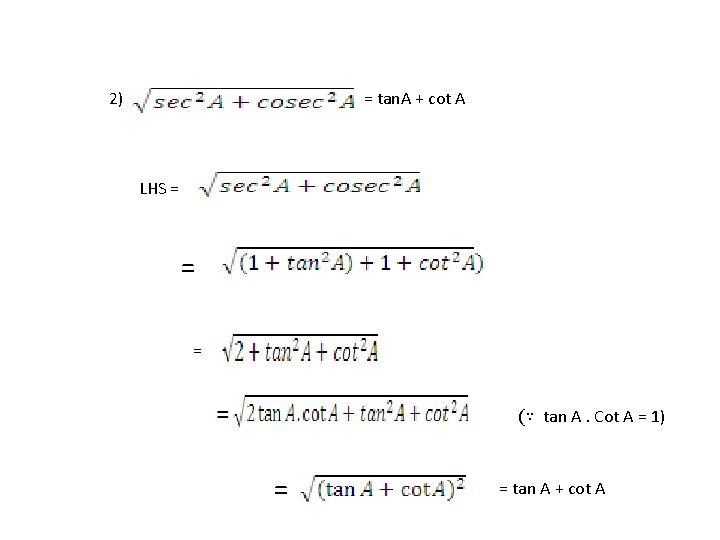
2) = tan. A + cot A LHS = = = (∵ tan A. Cot A = 1) = = tan A + cot A

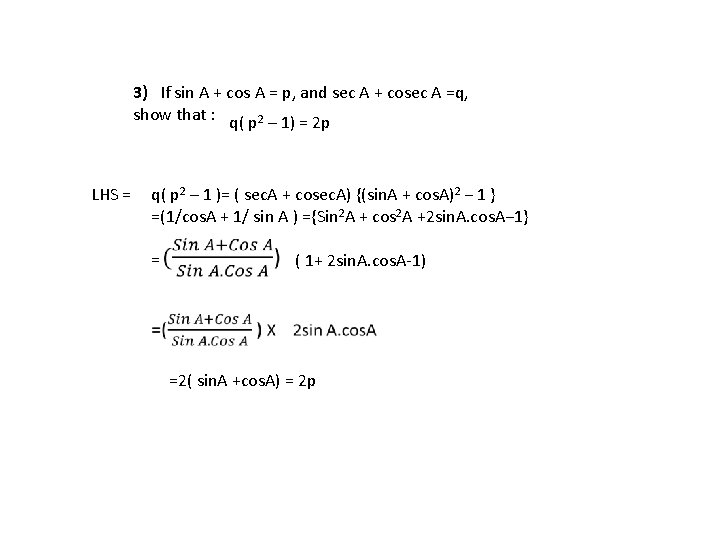
3) If sin A + cos A = p, and sec A + cosec A =q, show that : q( p 2 – 1) = 2 p LHS = q( p 2 – 1 )= ( sec. A + cosec. A) {(sin. A + cos. A)2 − 1 } =(1/cos. A + 1/ sin A ) ={Sin 2 A + cos 2 A +2 sin. A. cos. A− 1} = ( 1+ 2 sin. A. cos. A-1) =2( sin. A +cos. A) = 2 p

Prove the following identities: 1. cos A + sin. A = cos A Prove that : cos A – sin. A = sin. A 2. If tan A – sin A = n and tan A +sin A = m prove that m 2 - n 2= 4 3. If x = rsin. A cos. B , y = r sin A sin. B and z = r cos. A prove that r 2 = x 2 + y 2 + z 2

ART INTEGRATION

SUPER HEXAGON https: //youtu. be/Ylp 52 q. X 8 m. H 0

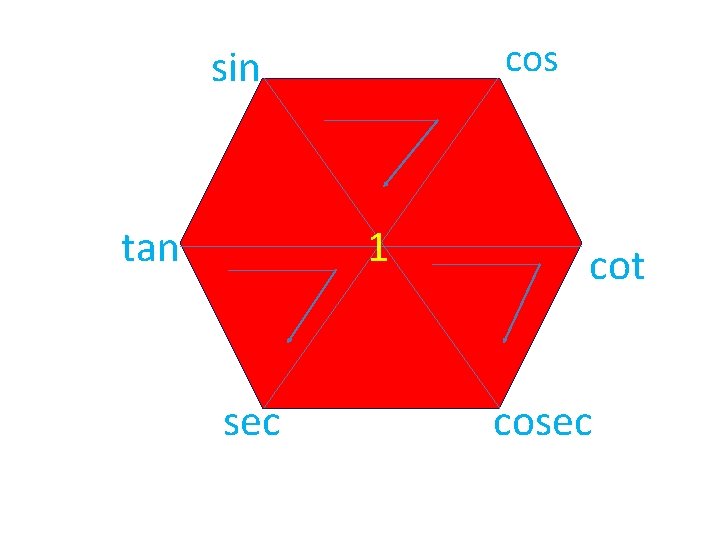
cos sin tan 1 sec cot cosec

TRICKS WE HAVE LEARNTS 1. SOH –CAH-TOA (MNEMONICS) 2. TRICKS TO REMEMBER TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES 3. SUPER HEXAGON 4. PALM TRICK METHOD

LEARNING OUTCOMES At the end of the chapter a child is able to : §Identify the hypotenuse, adjacent sides and opposite sides of an acute angle in a right angled triangle §Determine the six trigonometric ratios for a given angle in a right angled triangle. §Find the exact trigonometric function values for angles that measure 00, 300, 450 , 600 , 900 § Determine the relationship between the trigonometric ratios of complementary angles §Able to prove trigonometric identities and use it to prove other useful trigonometric identities

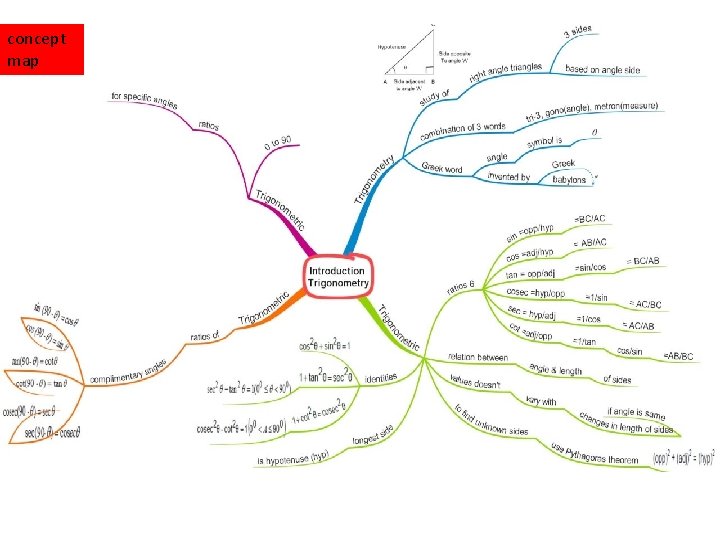
concept map

Thank you