Frequency Distribution Tables and Histogram September 6 2017

Frequency Distribution Tables and Histogram September 6, 2017

Making a Freq. Dist. Table for Grouped Data (w/ histogram) 1. 2. 3. 4. 5. 6. 7. 8. 9. Get the Highest and Lowest Scores. Get the range. (HS – LS) Determine the class width. (range) divided by (# of class intervals) Create your class intervals. Start w/ the lowest score. Tally your raw data. Determine frequency (f) Check completeness of raw data through cumulative frequency (cf) Get class mark for each interval. (lower limit + upper limit) divided by 2 Include class boundaries for each interval. (1 place value less than the lower/upper limit ; in half-unit increments ; to make the distribution of data continuous) Make a HISTOGRAM: x-axis (class boundaries); y-axis (frequency) Don’t forget your axis-break when necessary.
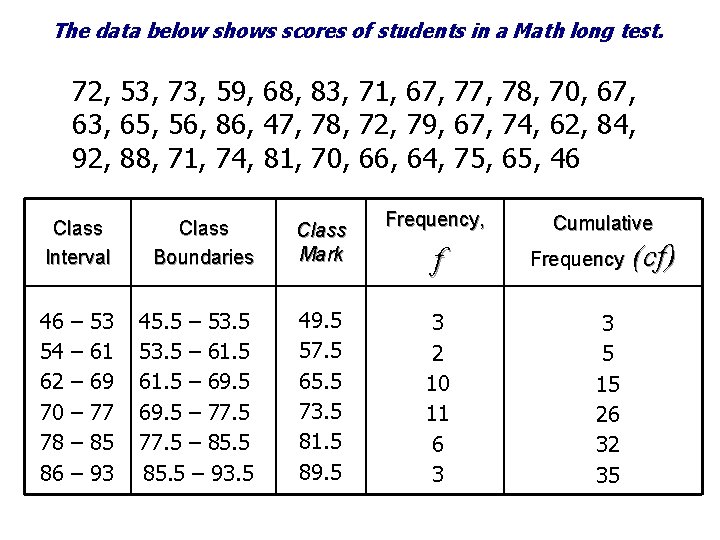
The data below shows scores of students in a Math long test. 72, 53, 73, 59, 68, 83, 71, 67, 78, 70, 67, 63, 65, 56, 86, 47, 78, 72, 79, 67, 74, 62, 84, 92, 88, 71, 74, 81, 70, 66, 64, 75, 65, 46 Class Interval 46 54 62 70 78 86 – – – 53 61 69 77 85 93 Class Boundaries Class Mark 45. 5 – 53. 5 – 61. 5 – 69. 5 – 77. 5 – 85. 5 – 93. 5 49. 5 57. 5 65. 5 73. 5 81. 5 89. 5 Frequency, f 3 2 10 11 6 3 Cumulative Frequency 3 5 15 26 32 35 (cf)
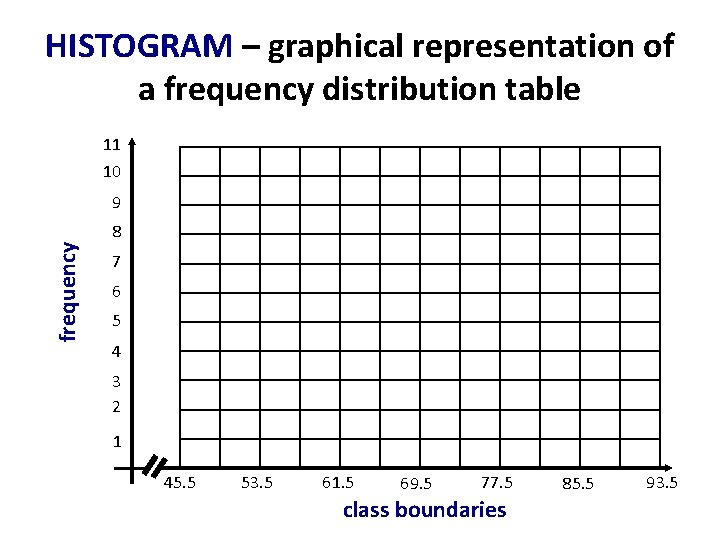
HISTOGRAM – graphical representation of a frequency distribution table 11 10 frequency 9 8 7 6 5 4 3 2 1 45. 5 53. 5 61. 5 69. 5 77. 5 class boundaries 85. 5 93. 5

Example: The histogram below shows the distribution of scores of students in a Math long test 11 Number of students 10 9 8 7 6 5 4 3 2 1 45. 5 53. 5 61. 5 69. 5 77. 5 SCORES 85. 5 93. 5
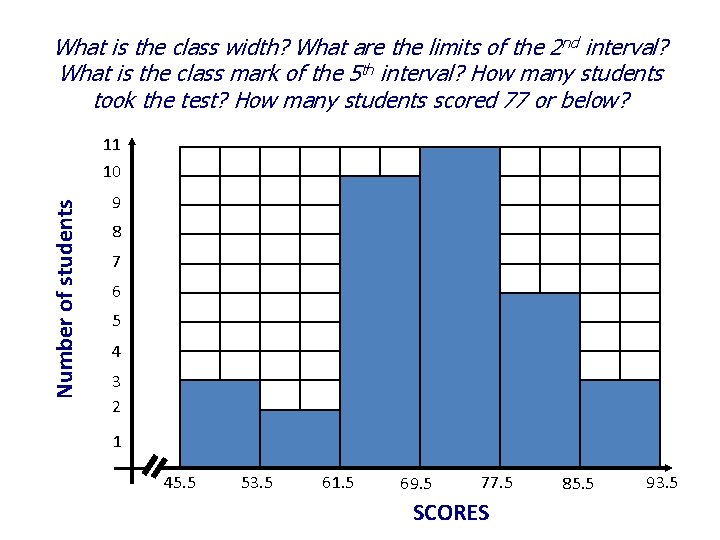
What is the class width? What are the limits of the 2 nd interval? What is the class mark of the 5 th interval? How many students took the test? How many students scored 77 or below? 11 Number of students 10 9 8 7 6 5 4 3 2 1 45. 5 53. 5 61. 5 69. 5 77. 5 SCORES 85. 5 93. 5
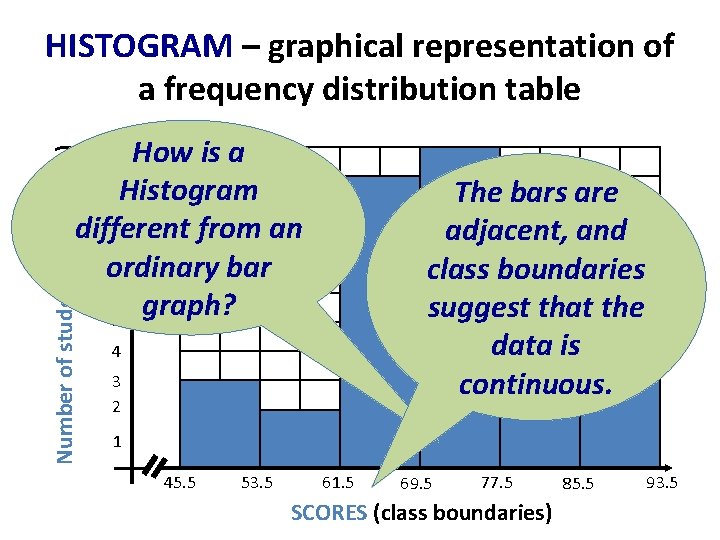
HISTOGRAM – graphical representation of a frequency distribution table Number of students (frequency) How is a 10 9 Histogram 8 different from an 7 ordinary bar 6 graph? 5 11 The bars are adjacent, and class boundaries suggest that the data is continuous. 4 3 2 1 45. 5 53. 5 61. 5 69. 5 77. 5 SCORES (class boundaries) 85. 5 93. 5
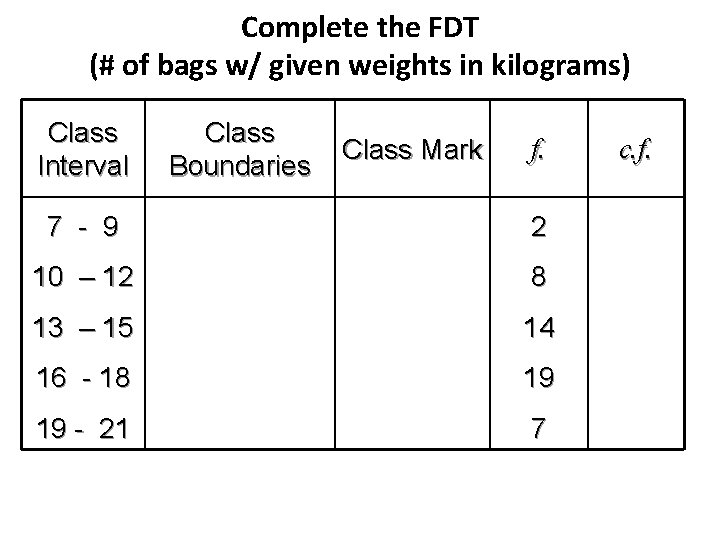
Complete the FDT (# of bags w/ given weights in kilograms) Class Interval Class Boundaries Class Mark f. 7 - 9 2 10 – 12 8 13 – 15 14 16 - 18 19 19 - 21 7 c. f.
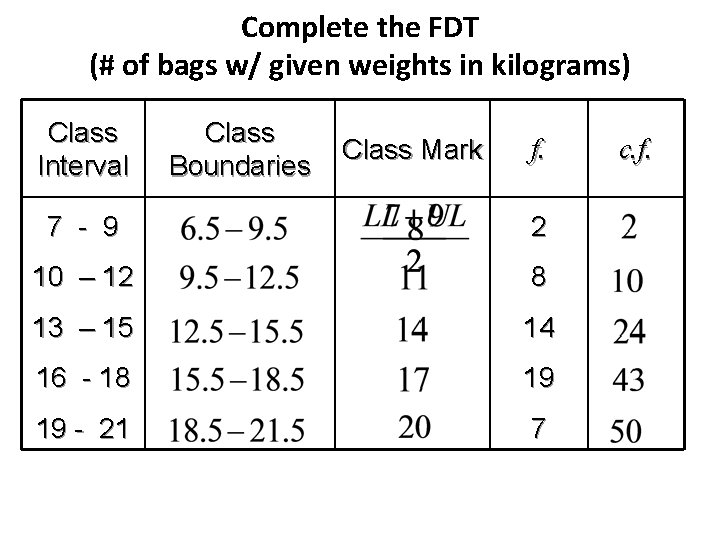
Complete the FDT (# of bags w/ given weights in kilograms) Class Interval Class Boundaries Class Mark f. 7 - 9 2 10 – 12 8 13 – 15 14 16 - 18 19 19 - 21 7 c. f.

Answer the questions. Class Interval Class Boundaries Class Mark f. 7 - 9 2 10 – 12 8 13 – 15 14 16 - 18 19 19 - 21 7 How many class intervals are there ? c. f. 5
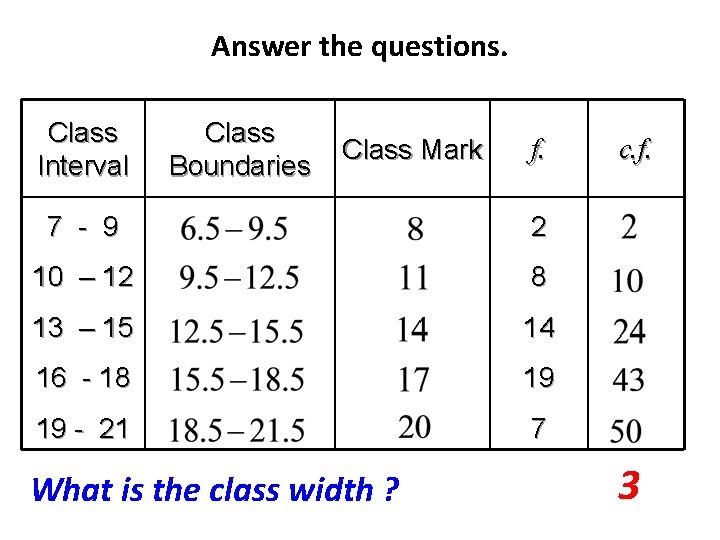
Answer the questions. Class Interval Class Boundaries Class Mark f. 7 - 9 2 10 – 12 8 13 – 15 14 16 - 18 19 19 - 21 7 What is the class width ? c. f. 3

Answer the questions. Class Interval Class Boundaries Class Mark f. 7 - 9 2 10 – 12 8 13 – 15 14 16 - 18 19 19 - 21 7 What bag weight is most frequent ? c. f. 15
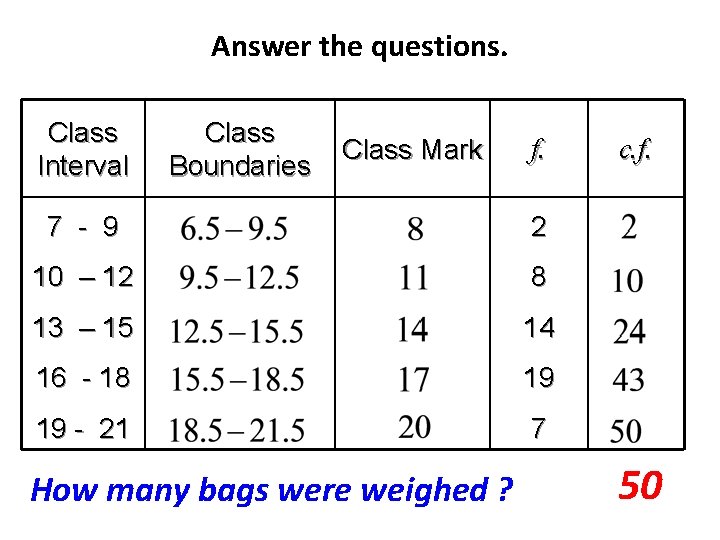
Answer the questions. Class Interval Class Boundaries Class Mark f. 7 - 9 2 10 – 12 8 13 – 15 14 16 - 18 19 19 - 21 7 How many bags were weighed ? c. f. 50

Answer the questions. Class Interval Class Boundaries Class Mark f. 7 - 9 2 10 – 12 8 13 – 15 14 16 - 18 19 19 - 21 7 c. f. How many bags weighed less than 16 kg ? 24

YOUR TURN! • Data shows the waistline of 24 students in AJHS. 32 31 28 27 33 29 31 29 32 30 33 30 28 27 36 30 27 26 28 29 29 28 29 27 • Make an FDT w/ 5 class intervals. • Determine the following: range, class width, class boundaries and class marks

STATISTICS: Measures of Central Tendency September 6, 2017
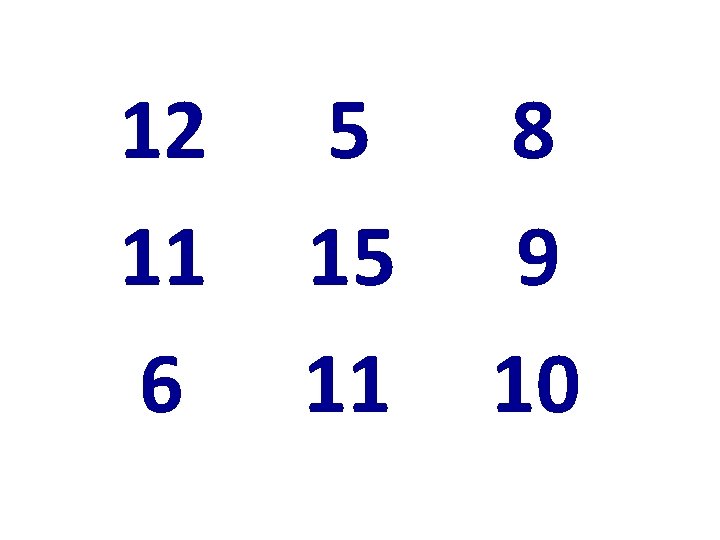
12 11 6 5 15 11 8 9 10

STATISTICS: Measures of Central Tendency FOR UNGROUPED DATA September 6, 2017

Objectives: Identify the 3 Measures of Central Tendency Compute for the MCT of ungrouped data Homework: Determine the formulas used to compute for the measures of central tendency of grouped data.

Source: http: //financemanila. net/2009/08/how-much-do-philippine-government-officials-make-in-salary/comment-page-1/ District Engineer Php 21, 655 Nurse Php 9, 939 Special Police Chief Php 20, 823 Teacher Php 15, 841 The typical salary of each of four occupations (government employees) is given above. On the average, who earns more, teachers or engineers?

Source: http: //financemanila. net/2009/08/how-much-do-philippine-government-officials-make-in-salary/comment-page-1/ District Engineer Php 21, 655 /mo Teacher Php 15, 841 / mo It appears from the data given that, on the average, engineers have greater income than teachers. However, take note that some teachers earn more than P 15, 841 per month and some engineers earn less than P 21, 655 per month.

Source: http: //financemanila. net/2009/08/how-much-do-philippine-government-officials-make-in-salary/comment-page-1/ District Engineer Php 21, 655 /mo Teacher Php 15, 841 / mo We want a single number that best represents the income of all engineers or all teachers. • not near the extremes • have to be in the center We are looking for an “average” income.

The most commonly used “averages” or Measures of Central Tendency are • Mean (or Arithmetic mean) • Median • Mode

Arithmetic mean (or simply mean) The mean of a set of numbers is the arithmetical average of the numbers; that is, the sum of all the numbers divided by the number of numbers

Arithmetic mean (or simply mean) Example: The recorded rainfall, in inches, for seven consecutive days in Rizal is given. 0. 25 0. 38 0. 03 0. 25 0. 56 mean = What do you think will happen to the mean if one 0. 25 was changed to 0. 90?

REMEMBER! The calculation of the mean involves ALL the data. Since it includes all data, having extreme values will affect the computation of the mean.

Median The median of a set of numbers is the middle number when the numbers are arranged in order. If there is an even number of numbers, the median is the mean of the two middle numbers.

Median Example: 0. 25 0. 38 0. 03 0. 25 0. 56 Arrange the numbers in order. 0. 03 median = 0. 03 0. 25 0. 38

REMEMBER! The calculation of the median involves just one or two middle values. Having extreme values will NOT really affect the computation of the median.

Mode The mode of a set of numbers is the most frequently occurring number. There may be more than one mode, or there may be no mode.

Mode Example: 0. 25 0. 38 mode = 0. 03 0. 25 0. 56

REMEMBER! The mode is easy to find but it does not take into consideration the bulk of the data. Also, the mode is NOT affected by extreme values. CMCasteloy. SY 10 -11 First Year Regular Pogram

Homework for Thursday, Sept 7. (Size-1, copy and answer. Show all necessary solutions) Find the mean, median and the mode of each set of data. Give the answers to 1 decimal place where necessary. a) 10, 12, 8, 9, 12, 14, 11, 15, 9, 12 b) 2. 3, 4. 1, 3. 7, 3. 2, 2. 8, 3. 6 Answers: a) mean: 11. 2 median: 11. 5 mode: 12 b) mean: 3. 3 median: 3. 4 no mode

YOUR TURN! Given this data set: 14. 5 14. 1 13. 3 12. 7 11. 4 What should be the value of z so that the mean is 12. 4 ? z

YOUR TURN! Find the mean, median and the mode in the FDT. Scores of a class in a 555 Quiz SCORE 5 4 3 2 1 0 f 4 5 5 4 2 0
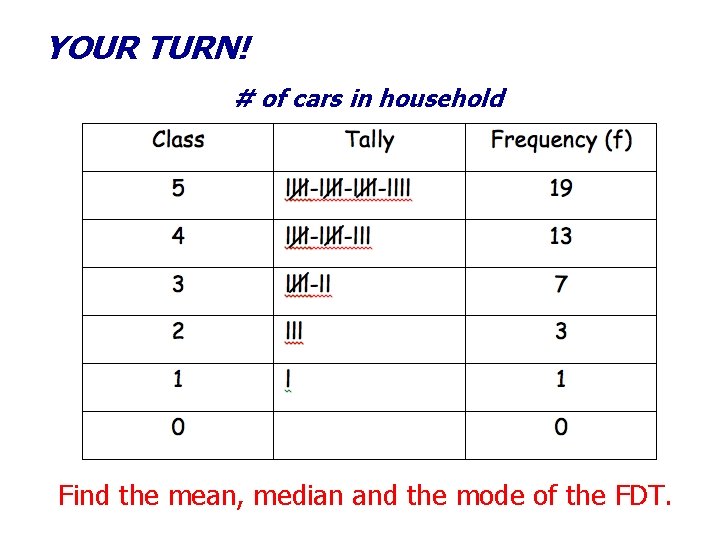
YOUR TURN! # of cars in household Find the mean, median and the mode of the FDT.

STATISTICS: Measures of Central Tendency FOR GROUPED DATA September 7, 2017

Frequency Distribution for the Weights of 50 Pieces of Luggage Class Interval Class Frequency Boundaries Mark x f 7 10 13 16 19 6. 5 9. 5 12. 5 15. 5 18. 5 - 9 – 12 – 15 - 18 - 21 – 9. 5 – 12. 5 – 15. 5 – 18. 5 – 21. 5 MODE for grouped data (grouped mode) 8 11 14 17 20 2 8 14 19 7 Cumulative Frequency (cf) 2 10 24 43 50
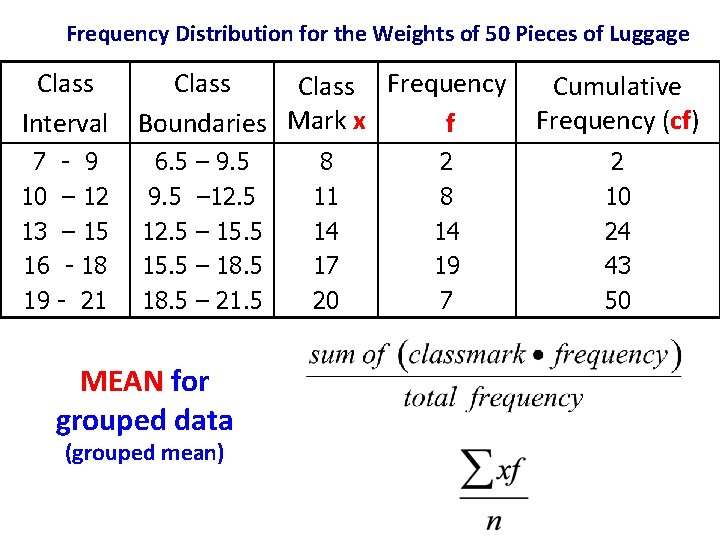
Frequency Distribution for the Weights of 50 Pieces of Luggage Class Interval Class Frequency Boundaries Mark x f 7 10 13 16 19 6. 5 9. 5 12. 5 15. 5 18. 5 - 9 – 12 – 15 - 18 - 21 – 9. 5 – 12. 5 – 15. 5 – 18. 5 – 21. 5 MEAN for grouped data (grouped mean) 8 11 14 17 20 2 8 14 19 7 Cumulative Frequency (cf) 2 10 24 43 50

Frequency Distribution for the Weights of 50 Pieces of Luggage Class Interval Class Frequency Boundaries Mark x f 7 10 13 16 19 6. 5 9. 5 12. 5 15. 5 18. 5 - 9 – 12 – 15 - 18 - 21 – 9. 5 – 12. 5 – 15. 5 – 18. 5 – 21. 5 MEDIAN for grouped data (grouped median) 8 11 14 17 20 2 8 14 19 7 Cumulative Frequency (cf) 2 10 24 43 50 L – lower boundary of median class H - size (class width) f – frequency (median class) N – total frequency C – cumulative frequency (before the median
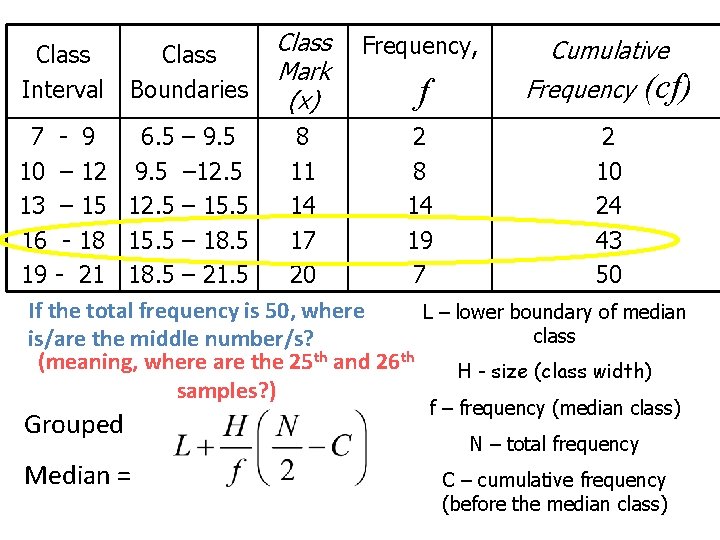
Class Interval Class Boundaries Class Mark (x) Frequency, f Cumulative Frequency (cf) 7 - 9 6. 5 – 9. 5 8 2 2 10 – 12 9. 5 – 12. 5 11 8 10 13 – 15 12. 5 – 15. 5 14 14 24 16 - 18 15. 5 – 18. 5 17 19 43 19 - 21 18. 5 – 21. 5 20 7 50 If the total frequency is 50, where L – lower boundary of median class is/are the middle number/s? (meaning, where are the 25 th and 26 th H - size (class width) samples? ) Grouped Median = f – frequency (median class) N – total frequency C – cumulative frequency (before the median class)
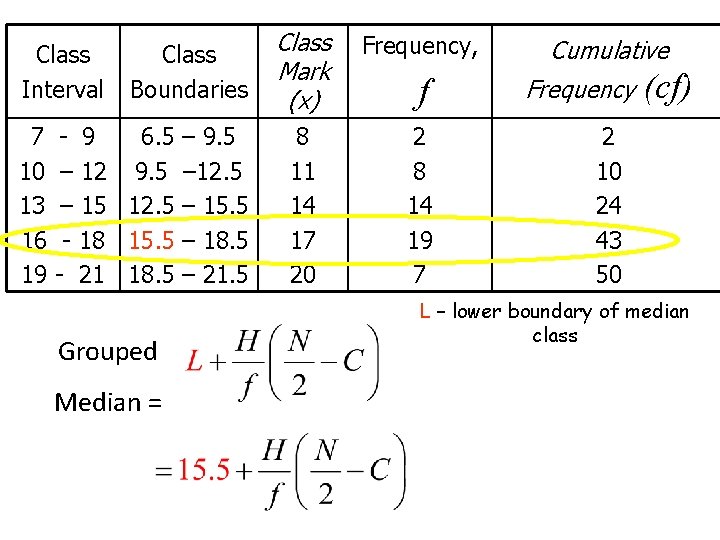
Class Interval 7 10 13 16 19 Class Boundaries - 9 6. 5 – 9. 5 – 12. 5 – 15. 5 - 18 15. 5 – 18. 5 - 21 18. 5 – 21. 5 Grouped Median = Class Mark (x) Frequency, 8 11 14 17 20 2 8 14 19 7 f Cumulative Frequency (cf) 2 10 24 43 50 L – lower boundary of median class
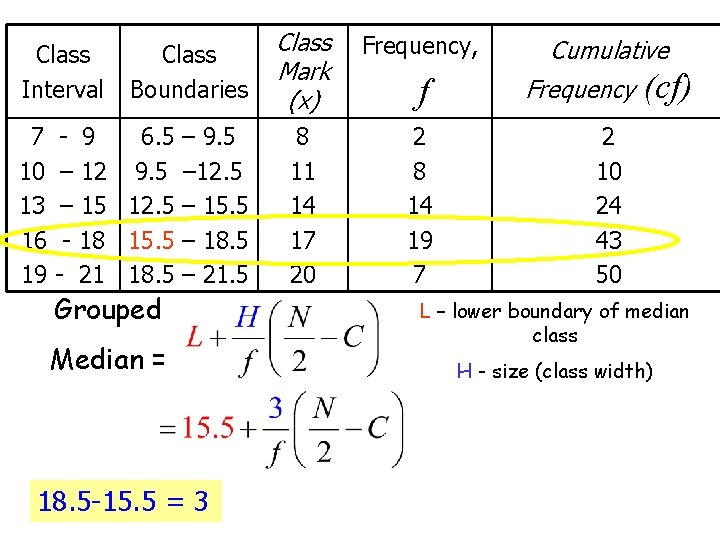
Class Interval 7 10 13 16 19 Class Boundaries - 9 6. 5 – 9. 5 – 12. 5 – 15. 5 - 18 15. 5 – 18. 5 - 21 18. 5 – 21. 5 Grouped Median = 18. 5 -15. 5 = 3 Class Mark (x) Frequency, 8 11 14 17 20 2 8 14 19 7 f Cumulative Frequency (cf) 2 10 24 43 50 L – lower boundary of median class H - size (class width)
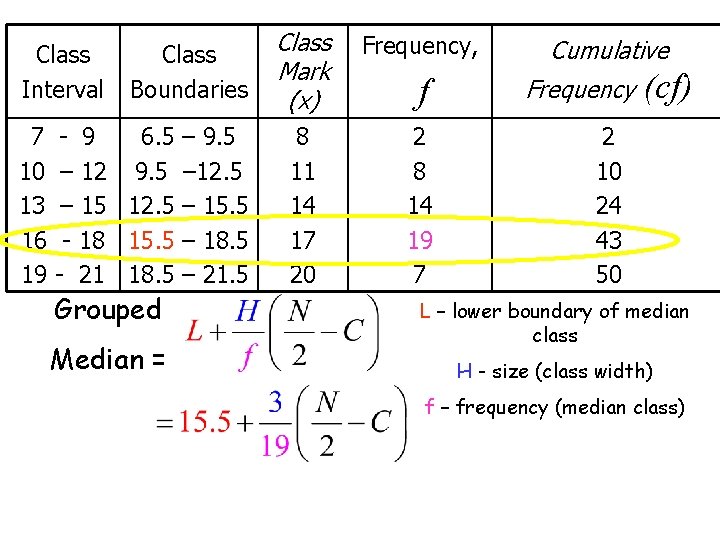
Class Interval 7 10 13 16 19 Class Boundaries - 9 6. 5 – 9. 5 – 12. 5 – 15. 5 - 18 15. 5 – 18. 5 - 21 18. 5 – 21. 5 Grouped Median = Class Mark (x) Frequency, 8 11 14 17 20 2 8 14 19 7 f Cumulative Frequency (cf) 2 10 24 43 50 L – lower boundary of median class H - size (class width) f – frequency (median class)

Class Interval 7 10 13 16 19 Class Boundaries - 9 6. 5 – 9. 5 – 12. 5 – 15. 5 - 18 15. 5 – 18. 5 - 21 18. 5 – 21. 5 Grouped Median = Class Mark (x) Frequency, 8 11 14 17 20 2 8 14 19 7 f Cumulative Frequency (cf) 2 10 24 43 50 L – lower boundary of median class H - size (class width) f – frequency (median class) N – total frequency 2+8+14+19+7=50

Class Interval 7 10 13 16 19 Class Boundaries - 9 6. 5 – 9. 5 – 12. 5 – 15. 5 - 18 15. 5 – 18. 5 - 21 18. 5 – 21. 5 Grouped Median = Class Mark (x) Frequency, 8 11 14 17 20 2 8 14 19 7 f Cumulative Frequency (cf) 2 10 24 43 50 L – lower boundary of median class H - size (class width) f – frequency (median class) N – total frequency C – cumulative frequency (before the median class)
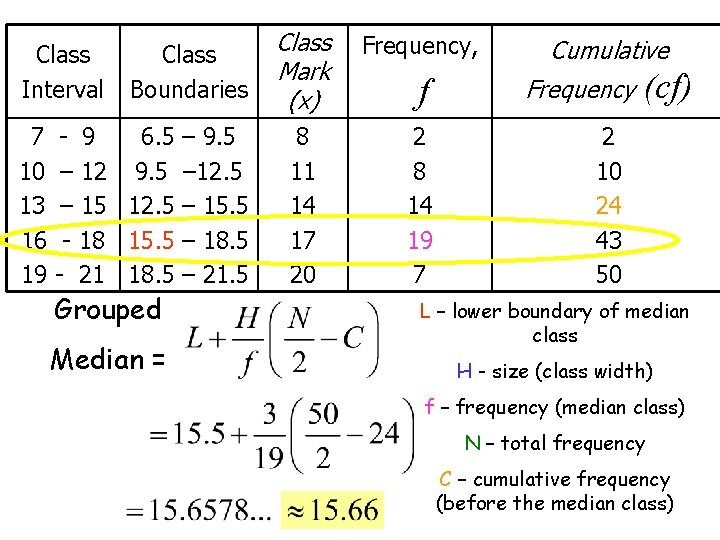
Class Interval 7 10 13 16 19 Class Boundaries - 9 6. 5 – 9. 5 – 12. 5 – 15. 5 - 18 15. 5 – 18. 5 - 21 18. 5 – 21. 5 Grouped Median = Class Mark (x) Frequency, 8 11 14 17 20 2 8 14 19 7 f Cumulative Frequency (cf) 2 10 24 43 50 L – lower boundary of median class H - size (class width) f – frequency (median class) N – total frequency C – cumulative frequency (before the median class)
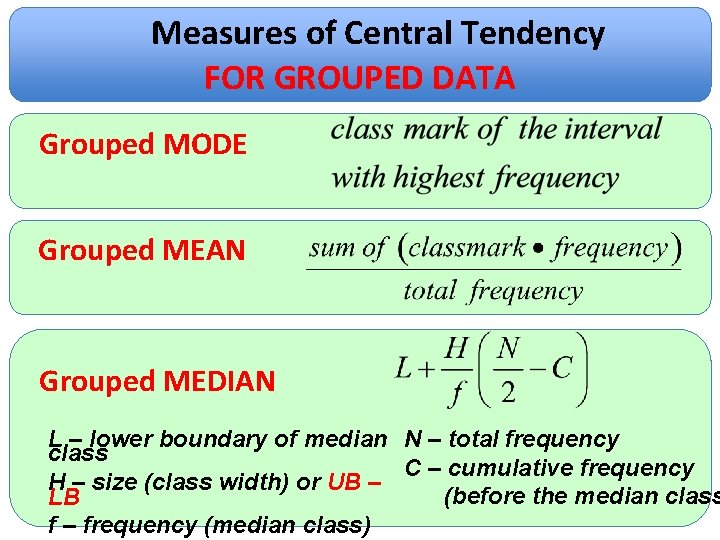
Measures of Central Tendency FOR GROUPED DATA Grouped MODE Grouped MEAN Grouped MEDIAN L – lower boundary of median N – total frequency class C – cumulative frequency H – size (class width) or UB – (before the median class LB f – frequency (median class)
- Slides: 48