Section 7 2 Verifying Trigonometric Identities Basic Trigonometric

Section 7 -2 Verifying Trigonometric Identities

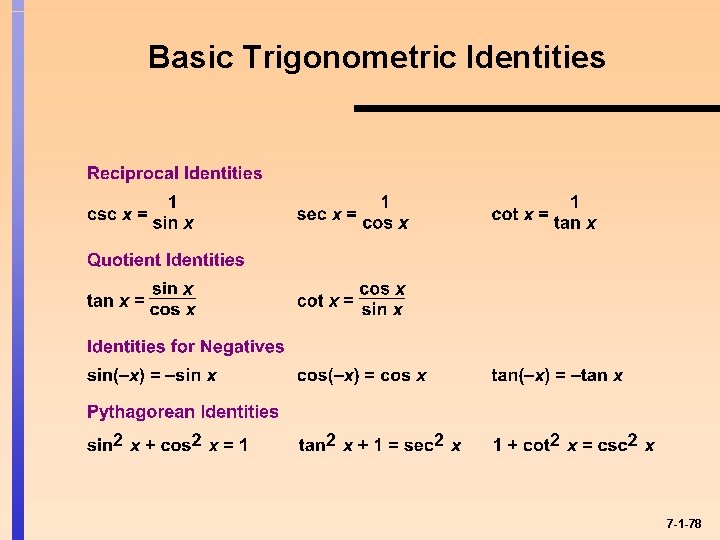
Basic Trigonometric Identities 7 -1 -78

Suggested Steps in Verifying Identities 1. Start with the more complicated side of the identity, and transform it into the simpler side. 2. Try algebraic operations such as multiplying, factoring, combining fractions, splitting fractions, and so on. 3. If other steps fail, express each function in terms of sine and cosine functions, and then perform appropriate algebraic operations. 4. At each step, keep the other side of the identity in mind. This often reveals what you should do in order to get there. 7 -1 -79

Sum, Difference, and Cofunction Identities Sum Identities sin(x + y) = sin x cos y + cos x sin y cos(x + y) = cos x cos y – sin x sin y tan x + tan y tan(x + y) = 1 – tan x y Difference Identities sin(x – y) = sin x cos y – cos x sin y cos(x – y) = cos x cos y + sin x sin y tan x – tan y tan(x – y) = 1 + tan x y Cofunction Identities æ çReplace è ö ÷ 2 with 90° if x is in degrees. ø æ cos ç 2 è – ö x÷ ø = sin x æ sin ç 2 è – ö x÷ ø = cos x æ tan ç 2 è ö – x÷ = cot x ø 7 -2 -80

Double and Half-Angle Identities 7 -3 -81

Product-Sum Identities Sum-Product Identities 7 -4 -82

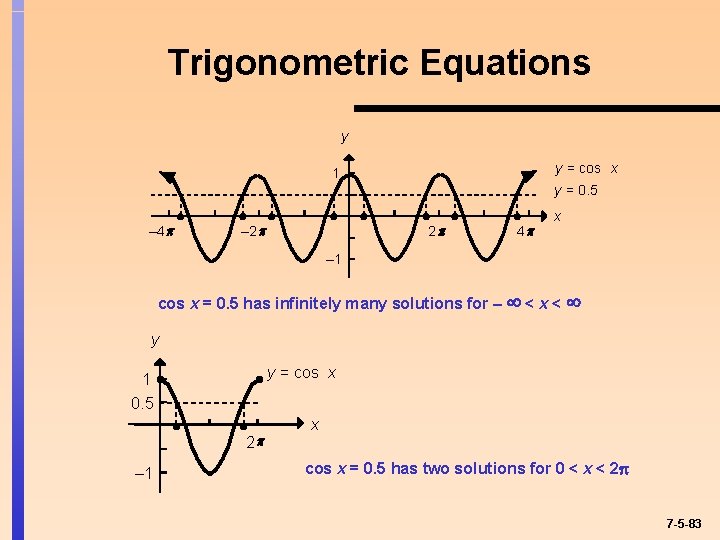
Trigonometric Equations y y = cos x 1 y = 0. 5 – 4 – 2 2 4 x – 1 cos x = 0. 5 has infinitely many solutions for – <x< y y = cos x 1 0. 5 2 – 1 x cos x = 0. 5 has two solutions for 0 < x < 2 7 -5 -83

Some Suggestions for Solving Trigonometric Equations 1. Regard one particular trigonometric function as a variable, and solve for it. 2. Consider using algebraic manipulation such as factoring. 3. Consider using identities. 4. After solving for a trigonometric function, solve for the variable following the procedures discussed in the preceding section. 7 -5 -84