Mathematical Models of Systems DNT 354 CONTROL PRINCIPLE

Mathematical Models of Systems DNT 354 – CONTROL PRINCIPLE Date: 17/06/2015 Prepared by: Nor Shaifudin Bin Abdul Hamid Email: norshaifudin@unimap. edu. my

CONTENTS Introduction Differential Equations of Physical Systems The Laplace Transform Transfer Function of Linear Systems Block Diagram

INTRODUCTIONS A mathematical model is a set of equations (usually differential equations) that represents the dynamics of systems. In practice, the complexity of the system requires some assumptions in the determination model. The equations of the mathematical model may be solved using mathematical tools such as the Laplace Transform. Before solving the equations, we usually need to linearize them.

DIFFERENTIAL EQUATIONS How do we obtain the equations? Physical law of the process Differential Equation Examples: i. ii. Mechanical system (Newton’s laws) Electrical system (Kirchhoff’s laws)

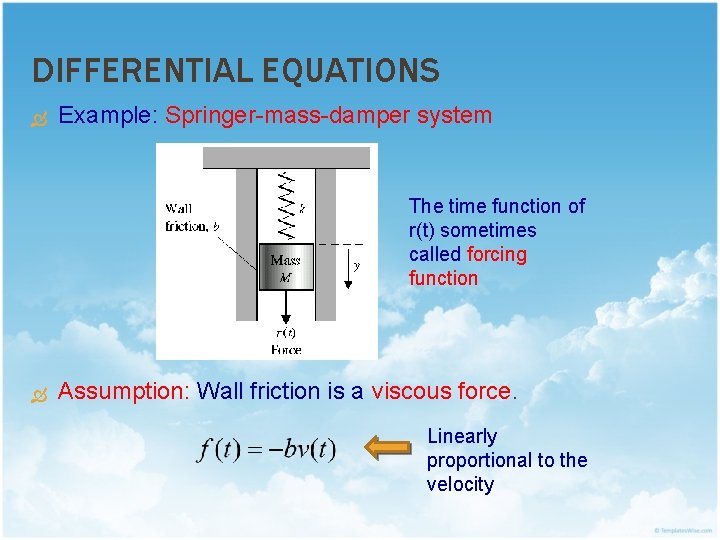
DIFFERENTIAL EQUATIONS Example: Springer-mass-damper system The time function of r(t) sometimes called forcing function Assumption: Wall friction is a viscous force. Linearly proportional to the velocity

DIFFERENTIAL EQUATIONS Example: Springer-mass-damper system (cont. ) Newton’s 2 nd Law:

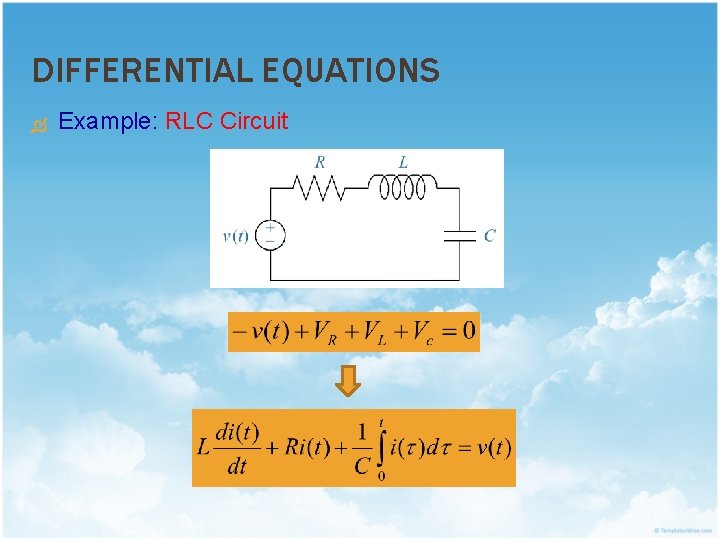
DIFFERENTIAL EQUATIONS Example: RLC Circuit

THE LAPLACE TRANSFORM The differential equations are transformed into algebraic equations, which are easier to solve. The Laplace transformation for a function of time, f(t) is: If, Similarly, Thus, , then,

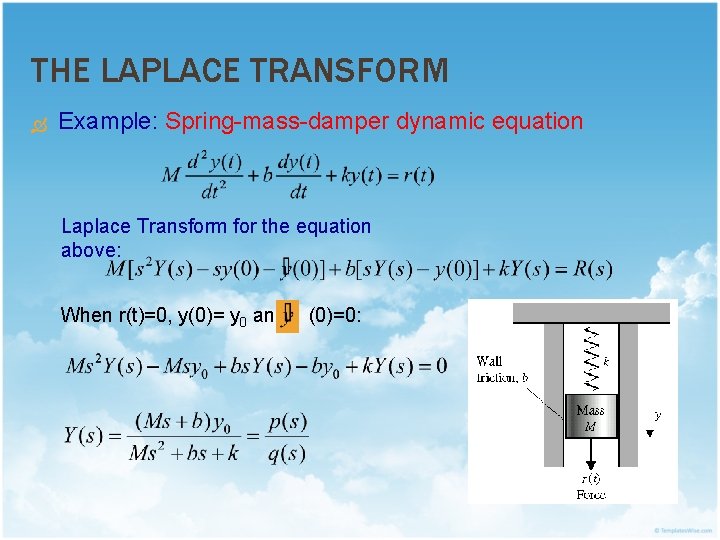
THE LAPLACE TRANSFORM Example: Spring-mass-damper dynamic equation Laplace Transform for the equation above: When r(t)=0, y(0)= y 0 and (0)=0:

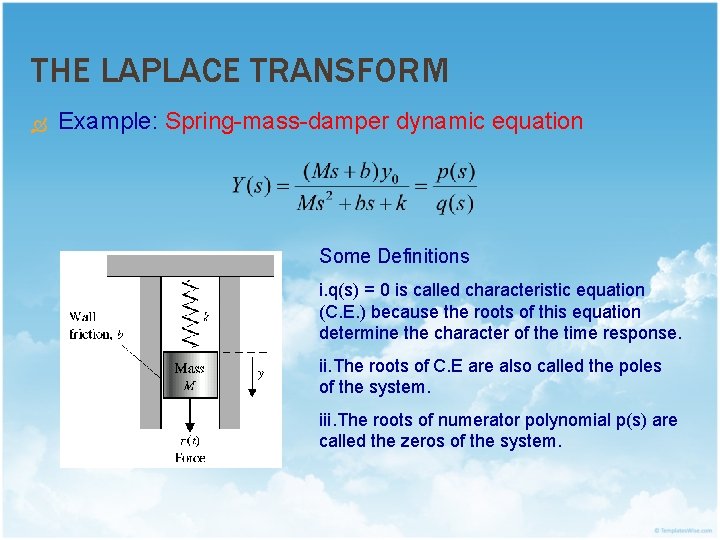
THE LAPLACE TRANSFORM Example: Spring-mass-damper dynamic equation Some Definitions i. q(s) = 0 is called characteristic equation (C. E. ) because the roots of this equation determine the character of the time response. ii. The roots of C. E are also called the poles of the system. iii. The roots of numerator polynomial p(s) are called the zeros of the system.

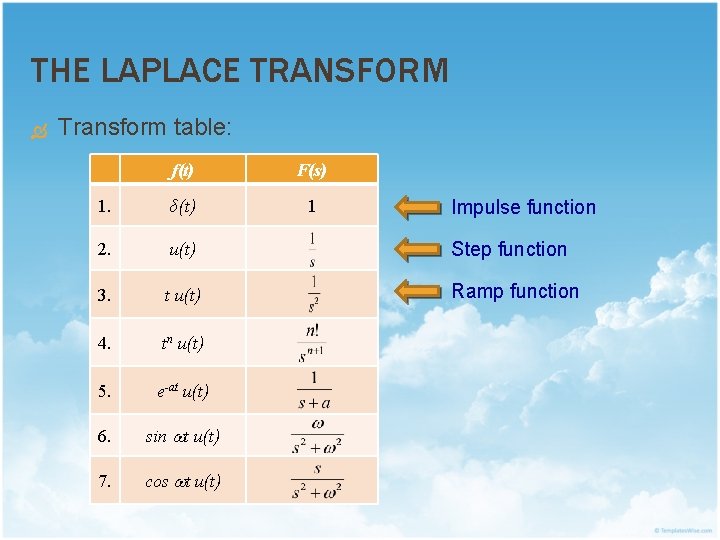
THE LAPLACE TRANSFORM Transform table: f(t) F(s) 1. δ(t) 1 2. u(t) Step function 3. t u(t) Ramp function 4. tn u(t) 5. e-at u(t) 6. sin t u(t) 7. cos t u(t) Impulse function

THE LAPLACE TRANSFORM Transform Properties

THE LAPLACE TRANSFORM Example: Find the Laplace Transform for the following. i. Unit function: ii. Ramp function: iii. Step function:

THE LAPLACE TRANSFORM Transform Theorem i. Differentiation Theorem ii. Integration Theorem: iii. Initial Value Theorem: iv. Final Value Theorem:

THE LAPLACE TRANSFORM The inverse Laplace Transform can be obtained using: Partial fraction method can be used to find the inverse Laplace Transform of a complicated function. We can convert the function to a sum of simpler terms for which we know the inverse Laplace Transform.

THE LAPLACE TRANSFORM We will consider three cases and show that F(s) can be expanded into partial fraction: i. Case 1: Roots of denominator A(s) are real and distinct. ii. Case 2: Roots of denominator A(s) are real and repeated. iii. Case 3: Roots of denominator A(s) are complex conjugate.

THE LAPLACE TRANSFORM Case 1: Roots of denominator A(s) are real and distinct. Example: Solution: It is found that: A = 2 and B = -2

THE LAPLACE TRANSFORM Case 1: Roots of denominator A(s) are real and distinct. Problem: Find the Inverse Laplace Transform for the following.

THE LAPLACE TRANSFORM Case 2: Roots of denominator A(s) are real and repeated. Example: Solution: It is found that: A = 2, B = -2 and C = -2

THE LAPLACE TRANSFORM Case 3: Roots of denominator A(s) are complex conjugate. Example: Solution: It is found that: A = 3/5, B = -3/5 and C = -6/5

THE LAPLACE TRANSFORM Case 3: Roots of denominator A(s) are complex conjugate. Example: Solution:

THE LAPLACE TRANSFORM Problem: Find the solution x(t) for the following differential equations. i. ii.

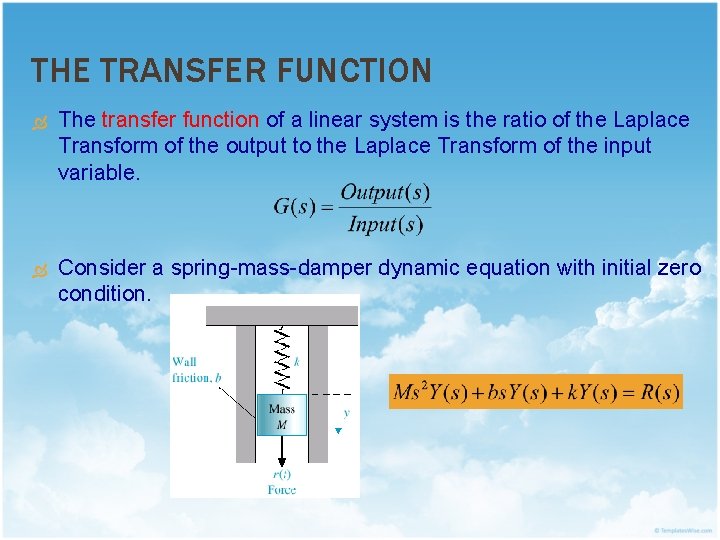
THE TRANSFER FUNCTION The transfer function of a linear system is the ratio of the Laplace Transform of the output to the Laplace Transform of the input variable. Consider a spring-mass-damper dynamic equation with initial zero condition.

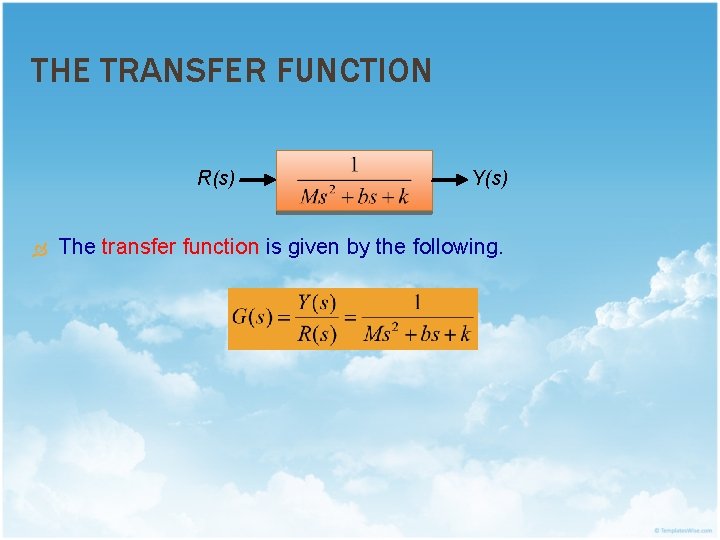
THE TRANSFER FUNCTION R(s) Y(s) The transfer function is given by the following.

THE TRANSFER FUNCTION Electrical Network Transfer Function Component V-I I-V V-Q Impedance Admittance

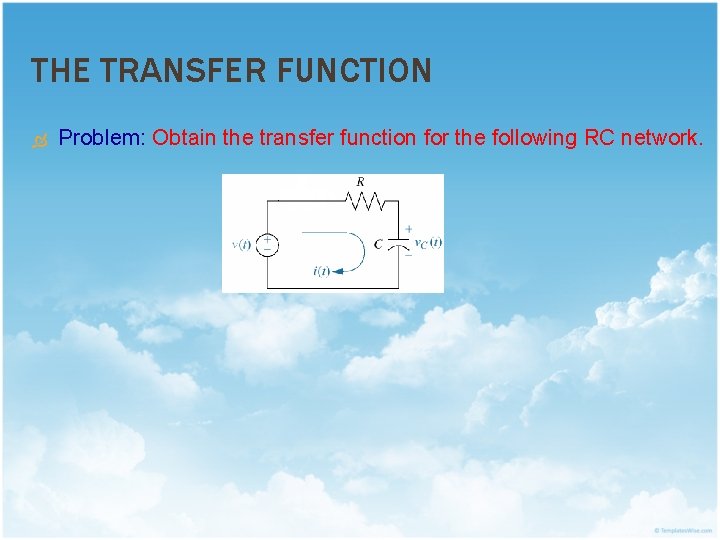
THE TRANSFER FUNCTION Problem: Obtain the transfer function for the following RC network.

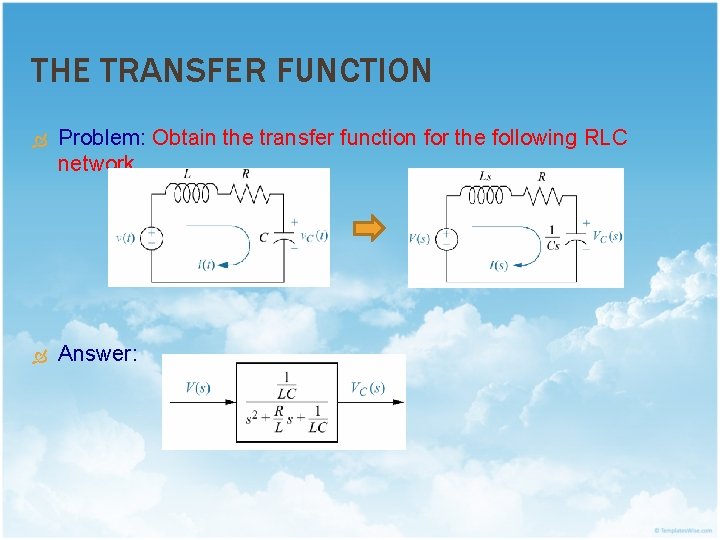
THE TRANSFER FUNCTION Problem: Obtain the transfer function for the following RLC network. Answer:

THE TRANSFER FUNCTION Op-Amp Circuit Transfer Function § Frequently used to amplify signal in sensor circuits. § § e 1 and e 2 are relative to ground. e 1 to the -ve terminal of the amplifier is inverted, and e 2 to the +ve terminal. The total input to the amplifier is e 2 -e 1. So, we have: The operating conditions for ideal op-amp: i. ii. i 1 = i 2 = 0 (∞ input impedance) e 1 = e 2

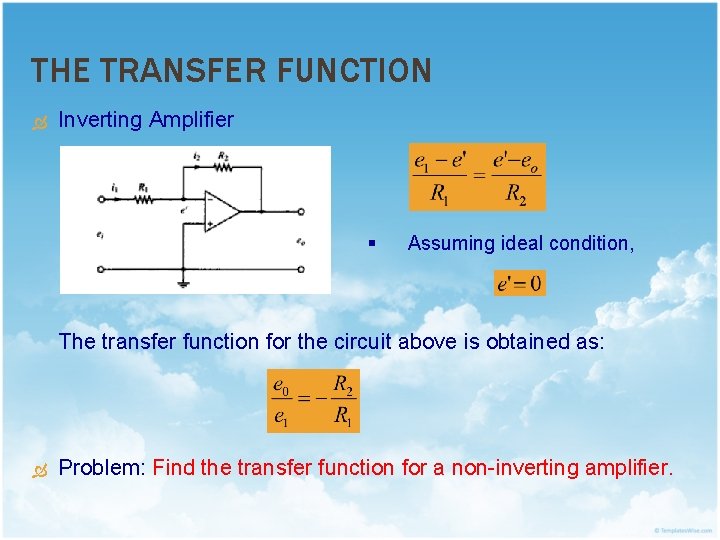
THE TRANSFER FUNCTION Inverting Amplifier § Assuming ideal condition, The transfer function for the circuit above is obtained as: Problem: Find the transfer function for a non-inverting amplifier.

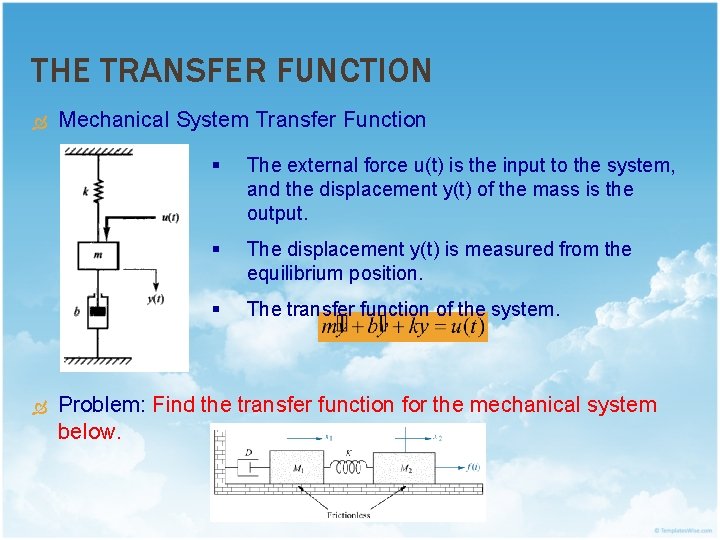
THE TRANSFER FUNCTION Mechanical System Transfer Function § The external force u(t) is the input to the system, and the displacement y(t) of the mass is the output. § The displacement y(t) is measured from the equilibrium position. § The transfer function of the system. Problem: Find the transfer function for the mechanical system below.

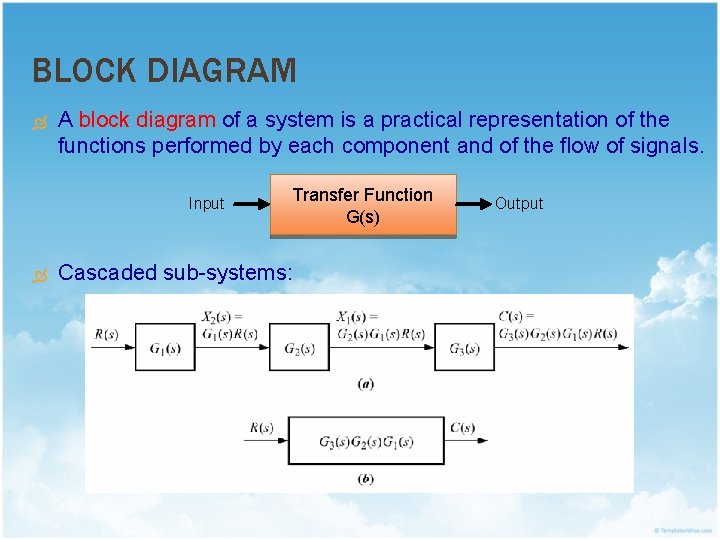
BLOCK DIAGRAM A block diagram of a system is a practical representation of the functions performed by each component and of the flow of signals. Input Transfer Function G(s) Cascaded sub-systems: Output

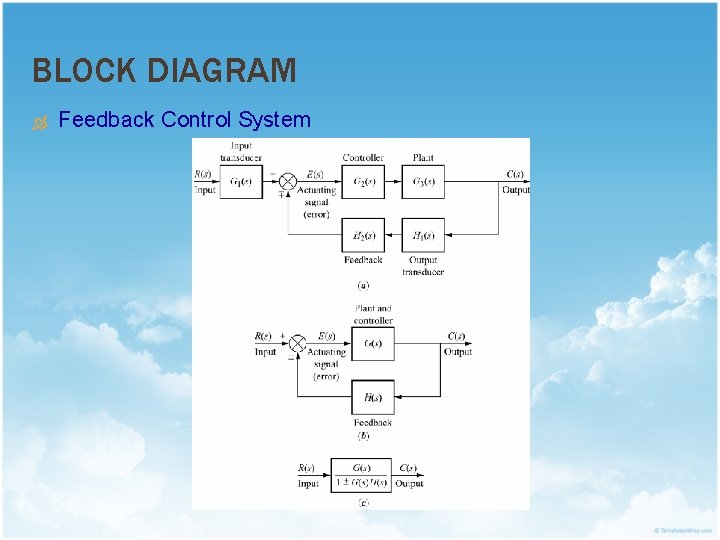
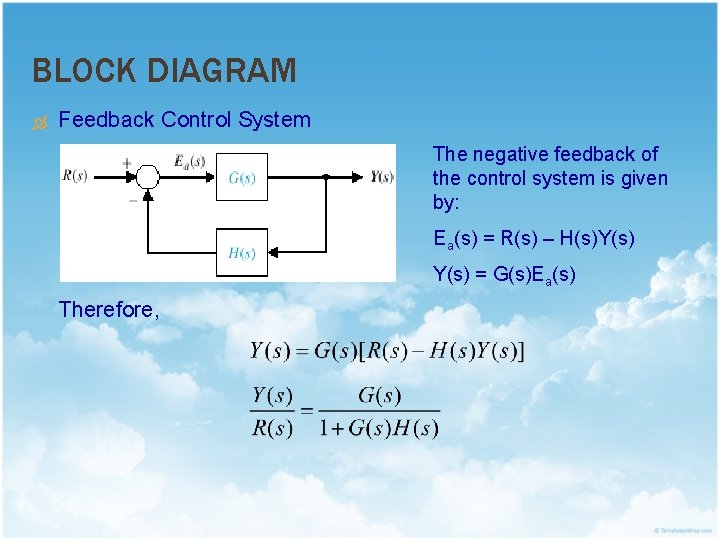
BLOCK DIAGRAM Feedback Control System

BLOCK DIAGRAM Feedback Control System The negative feedback of the control system is given by: Ea(s) = R(s) – H(s)Y(s) = G(s)Ea(s) Therefore,

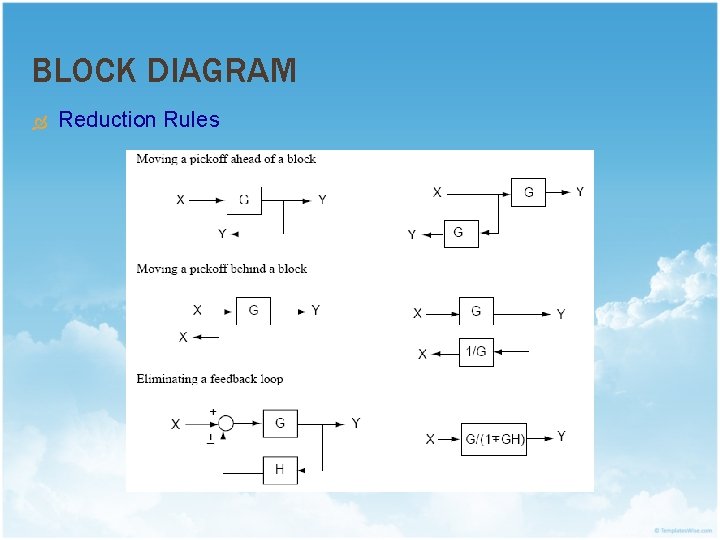
BLOCK DIAGRAM Reduction Rules

BLOCK DIAGRAM Reduction Rules

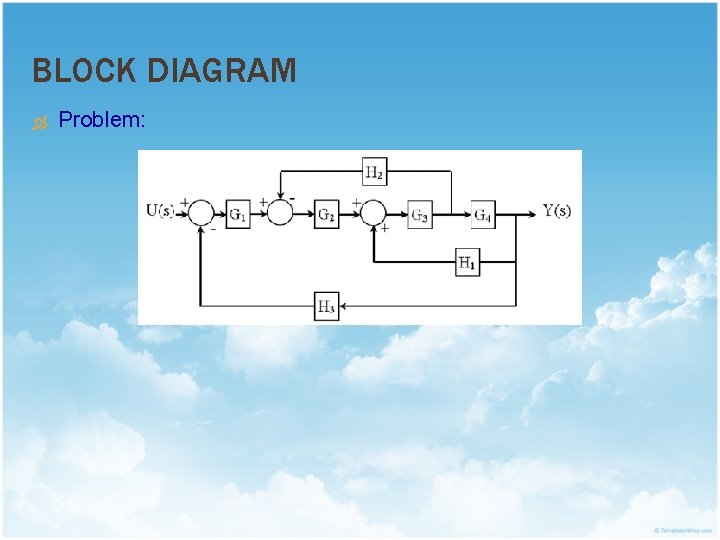
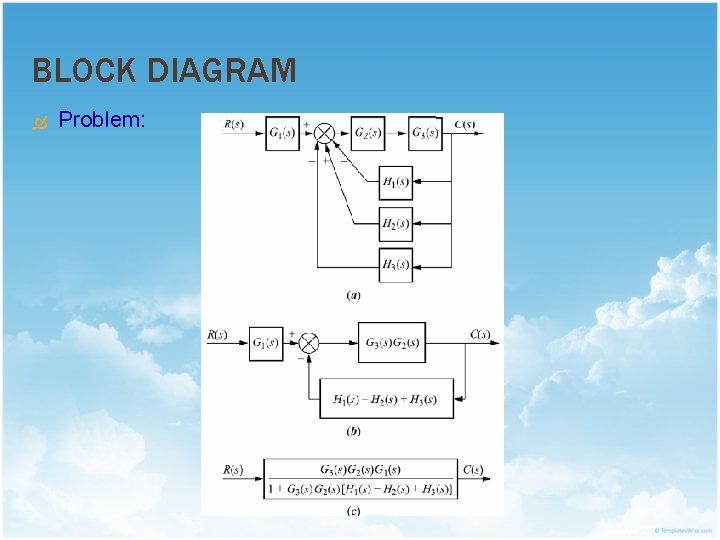
BLOCK DIAGRAM Problem:

BLOCK DIAGRAM Problem:

FURTHER READING… Chapter 2 i. ii. Dorf R. C. , Bishop R. H. (2001). Modern Control Systems (9 th Ed), Prentice Hall. Nise N. S. (2004). Control System Engineering (4 th Ed), John Wiley & Sons.

“The whole of science is nothing more than a refinement of everyday thinking…” THE END…