Approach to Impact Prediction Mathematical Model Mathematical models


















- Slides: 35

Approach to Impact Prediction

Mathematical Model

Mathematical models can be described according to the following features: 1. 2. – – – 3. 4. – – Empirical or internally descriptive: empirical because they can be derived solely on the basis of statistical analysis of observations from the environment to find the "best fit" equation (empirical models are sometimes called “black box” models); or · internally descriptive because equations are based on a priori understanding of the relationship between variables. The equations therefore represent some theory or assumption of how the environment works. Generalized or site-specific: generalized, as they can be applicable to a range of different environment allocations which meet certain specific characteristics; or site-specific, as they can be developed or applied only to a specific environmental location. Stationary or dynamic: stationary, if conditions in the model are fixed over the period of the prediction; or dynamic, if the predictions are made over a period of time in which conditions in the environment change.

4. Homogeneous or non-homogeneous: – – 5. homogeneous, as they can assume that conditions at the source prevail throughout the area over which predictions are made; or non-homogeneous, as environmental conditions affecting the predicted outcome vary with distance from the source. Deterministic or stochastic: – – deterministic, as input variables and relationships are fixed quantities and the predicted outcome from a given starting point is a single, unique value; or stochastic, as simple variables and parameters may be described probabilistically. These models reflect the natural variations occurring in the environment and results are presented as a frequency distribution of probable outcomes rather than as a single value.

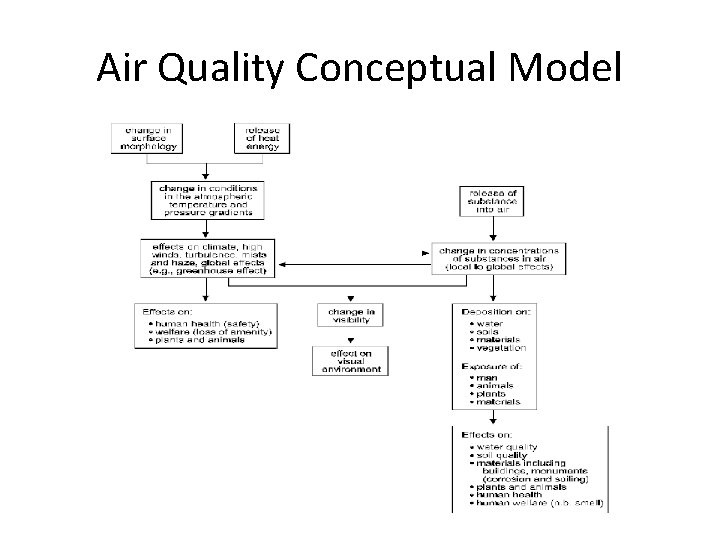
Air Quality Conceptual Model

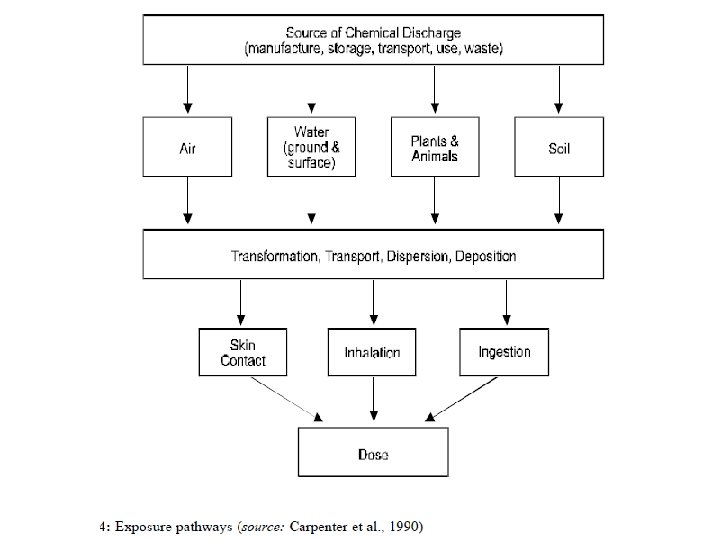
Three aspects of air quality problems 1. estimating rates of release of pollutants; 2. predicting atmospheric concentrations of pollutants; and 3. predicting deposition rates on pollutants on soil, water, and vegetation.

Estimating Air Release

Dispersion Model 1. – – – – 2. – – – – plume rise; advection transport by wind; vertical, lateral, and horizontal diffusion caused by turbulence; reflection from the ground and from the top of the mixing layer; physical-chemical transformation of pollutants in air, including radioactive decay, photochemical reactions, and aerosol formation; gravitational settling of particulate pollutants; dry deposition, that is, uptake of substances onto soil or other surface material by chemical, biological, or physical processes occurring at the interface; wet deposition, that is, rain-out and wash-out of substances onto the surface; behavior of plumes in response to variations in the land surface; entrainment of plumes in the lee of buildings; variations in atmospheric diffusion conditions with height above the surface; variations in emission rate and/or in meteorological conditions over the period of prediction; variations in meteorological and/or topographical conditions with distance from the source; and random variation in environmental conditions and emissions.

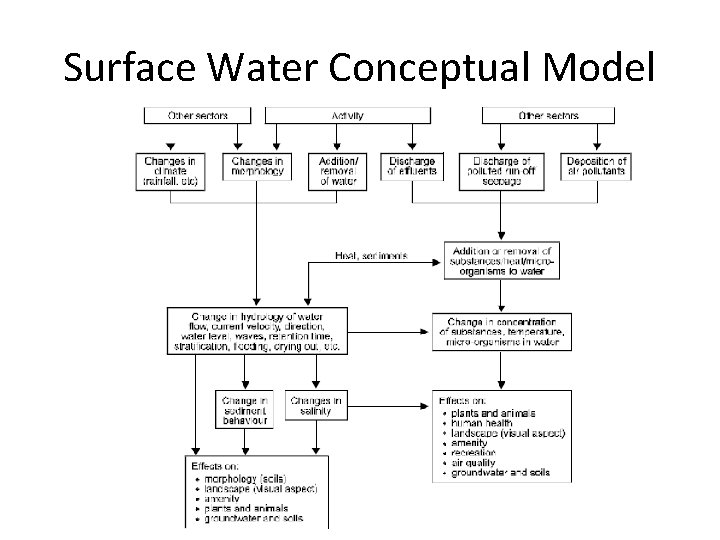
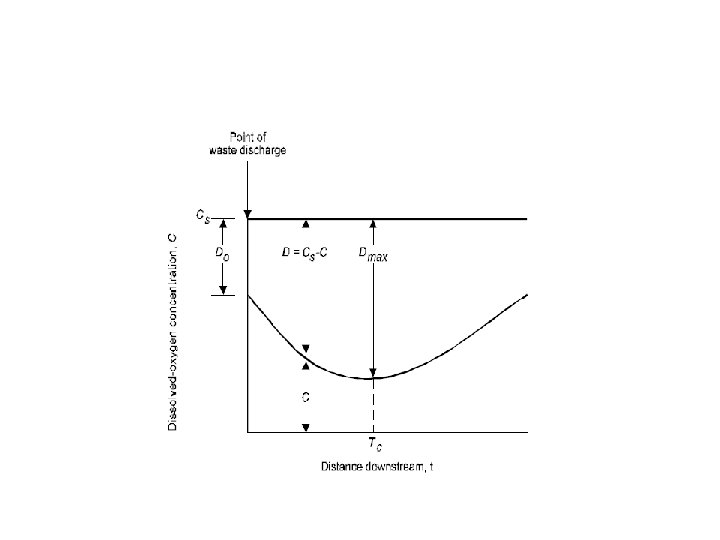
Surface Water Conceptual Model


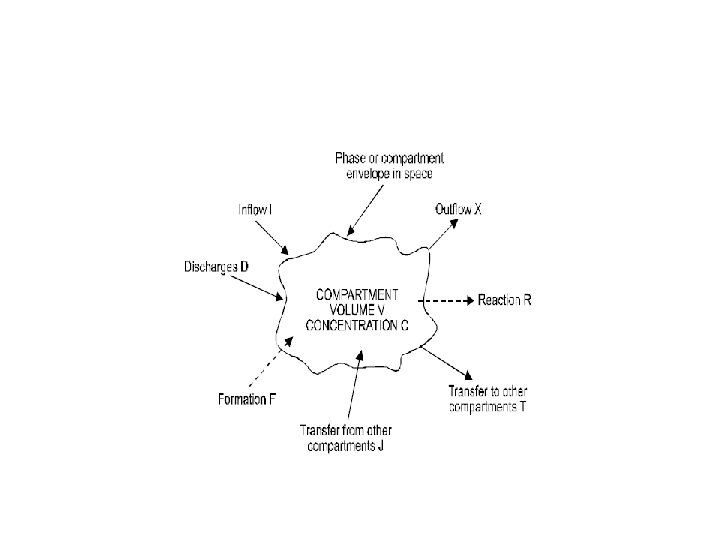
Water Quality Mass Balance


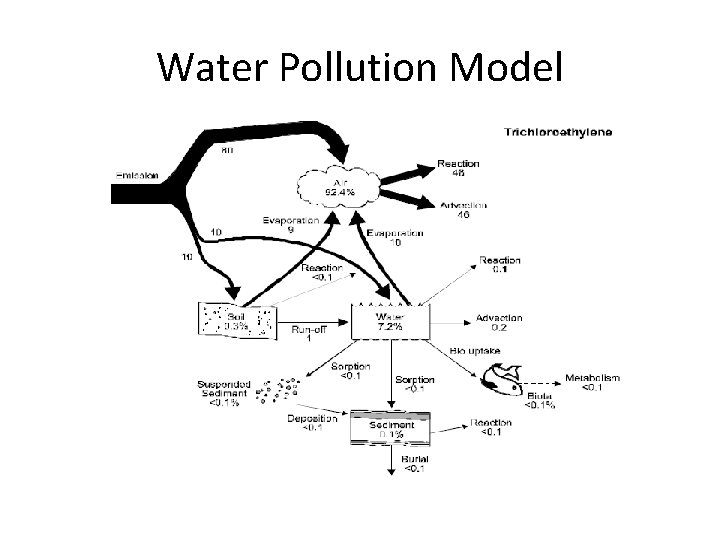
Water Pollution Model

Erosion and Sedimentation Model

Darcy’s Law

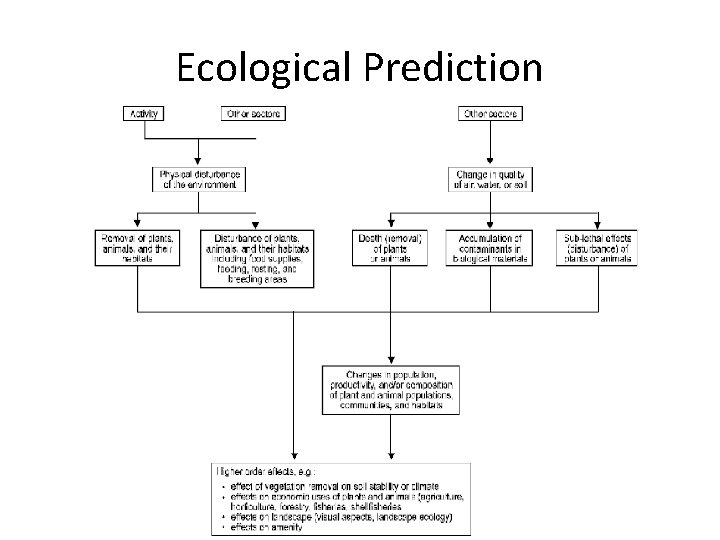
Ecological Prediction











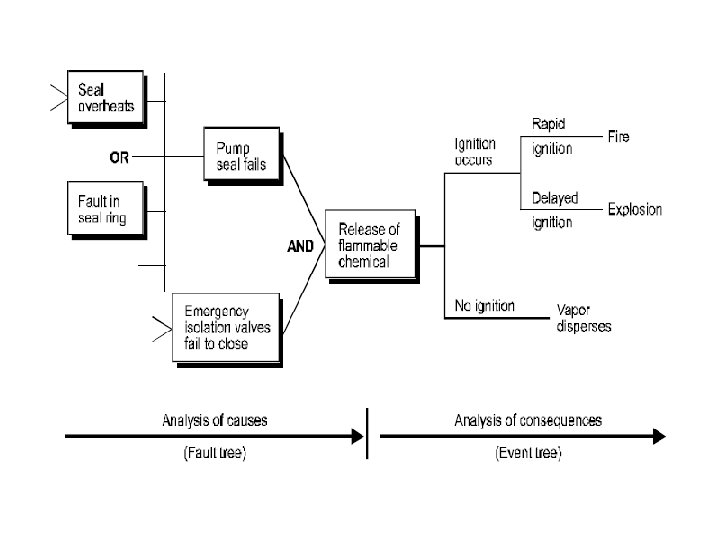
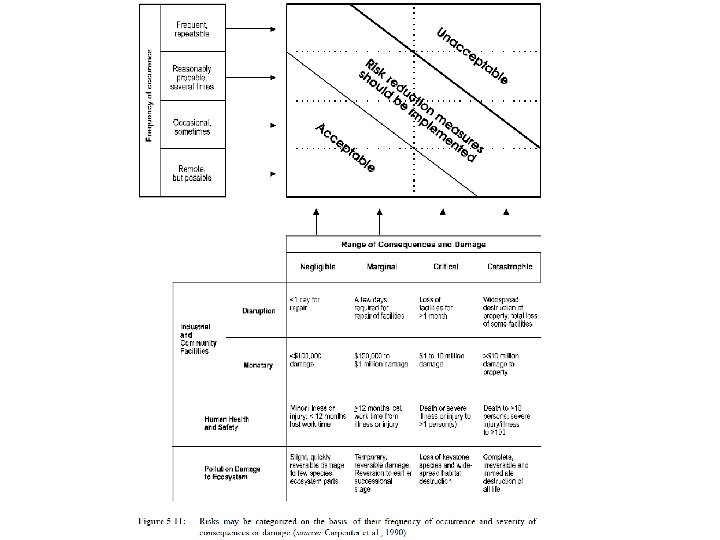
• ERA addresses four questions: • · What can go wrong to cause adverse consequences? • · What is the probability of frequency of occurrence of adverse consequences? • · What are the range and distribution of the severity of adverse consequences? • · What can be done, at what cost, to manage and reduce unacceptable risks and damage?

The five step sequence in performing ERA is: 1. hazard identification - sources of adverse impacts; 2. hazard accounting - scoping, setting the boundaries of the ERA; 3. scenarios of exposure - how the hazard might be encountered; 4. risk characterization - likelihood and severity of impact damage; and 5. risk management - mitigation or reduction of unacceptable risk.






ADKL KEPMENKES 876/2001 • Model kajian dampak lingkungan dengan pendekatan ARKL • Bertujuan untuk mengenal, memahami & meramalkan kondisi & karakteristik lingkungan yang berpotensi menimbulkan risiko kesehatan • Hasil ADKL menjadi dasar untuk menyusun atau mengembangkan pengelolaan dan pemantauan risiko

I= intake (asupan), jumlah risk agent yang masuk, (mg/kg/hari) C= konsentrasi risk agent, mg/M 3 (udara), mg/L (air minum), mg/kg (makanan) R= laju (rate) asupan, 20 M 3/hari (udara), 2 L/hari (air minum? ) t. E = waktu pajanan harian, jam/hari f. E = frekuensi pajanan tahunan, hari/tahun Dt = durasi pajanan, real time atau 30 tahun proyeksi Wb = berat badan, kg tavg = perioda waktu rata-rata, 30 tahun 365 hari/tahun (non karsinogen) atau 70 tahun 365 hari/tahun (karsinogen )
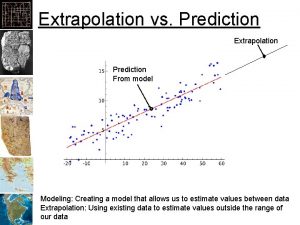
 Mathematical models for impact prediction
Mathematical models for impact prediction Stealing machine learning models via prediction apis
Stealing machine learning models via prediction apis Stealing machine learning models via prediction apis
Stealing machine learning models via prediction apis Mathematical economics vs non mathematical economics
Mathematical economics vs non mathematical economics Modeling real world data with sinusoidal functions
Modeling real world data with sinusoidal functions Conceptual physical and mathematical models are used to
Conceptual physical and mathematical models are used to Linear functions as mathematical models
Linear functions as mathematical models Linear functions as mathematical models
Linear functions as mathematical models Types of mathematical models
Types of mathematical models Difference between modals and semi modals
Difference between modals and semi modals How did tycho brahe and kepler employ the scientific method
How did tycho brahe and kepler employ the scientific method Attrition prediction model in excel
Attrition prediction model in excel Differences between virtual circuits and datagram networks
Differences between virtual circuits and datagram networks Theoretical models of counseling
Theoretical models of counseling Waterfall approach in international marketing
Waterfall approach in international marketing Multiple conflict
Multiple conflict Cognitive approach vs behavioral approach
Cognitive approach vs behavioral approach Approach approach
Approach approach Approach to system development
Approach to system development Deep learning approach and surface learning approach
Deep learning approach and surface learning approach Impact business model canvas
Impact business model canvas Environmental science sustaining your world
Environmental science sustaining your world Ipat model
Ipat model Ipat model of environmental impact
Ipat model of environmental impact Ipat model
Ipat model What is assure
What is assure Social impact model
Social impact model Profit impact of market strategy pims model
Profit impact of market strategy pims model High impact change model
High impact change model Will/won't/may/might for predictions
Will/won't/may/might for predictions Championship branch prediction
Championship branch prediction Corner prediction
Corner prediction Hunger games questions by chapter
Hunger games questions by chapter Phd secondary structure prediction
Phd secondary structure prediction Standard error of prediction
Standard error of prediction Merit pridiction
Merit pridiction