Chapter 1 Linear Functions and Mathematical Modeling Section

Chapter 1 Linear Functions and Mathematical Modeling Section 1. 5

Section 1. 5 Linear Functions: Equations and Graphs • Definition of a Linear Function • Modeling with Linear Functions • Finding the Equation of a Linear Function: Slope-Intercept Form, Point-Slope Form • Horizontal and Vertical Lines • Parallel and Perpendicular Lines

Definition of a Linear Function A linear function can be written in the form f(x) = ax + b, where a and b are constants (fixed values). Examples: y = – 8 x + 2; f(x) = – 5; h(t) = ½ – 9 t represent linear functions f(x) = x 3 – 2 x; y = 8 x + 9; h(t) = 1/t do not represent linear functions

Linear Functions Notes: 1. The graph of a linear function is a straight line. 2. The input and output variables can only be raised to the first power. 3. The rate of change (slope) of a linear function f(x) = mx + b is given by m. 4. A linear function has a constant rate of change. 5. The vertical intercept of a linear function f(x) = mx + b is given by b.

For each linear function, identify the rate of change (slope), m, and the vertical intercept, b. a. f(x) = 17. 5 – 10 x b. 3/5 + y = x c. 3. 4 x – f(x) = 7 Note: Before we identify m and b, f(x) must be isolated! a. m = – 10 b = 17. 5 b. m = 1 b = – 3/5 c. m = 3. 4 b = – 7

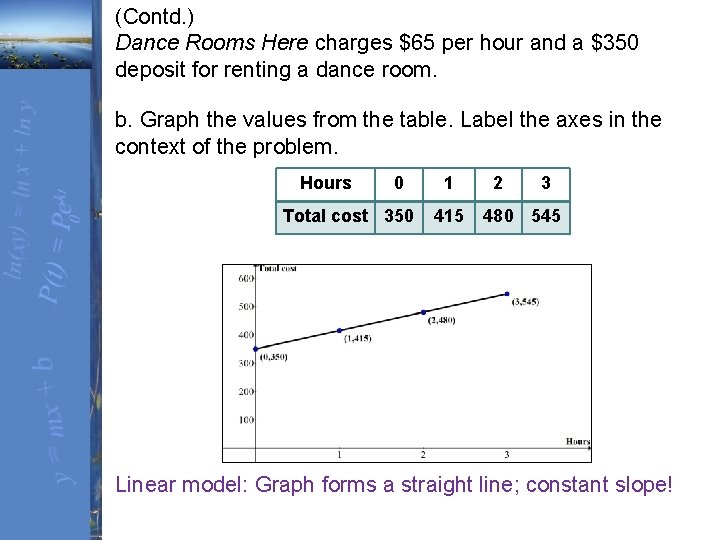
Dance Rooms Here charges $65 per hour and a $350 deposit for renting a dance room. a. Create a table that represents the total cost for renting a dance room from 0 to 3 hours. Total cost = deposit plus rate per hour 0 hours: 1 hour: 2 hours: 350 + 65(0) = 350 + 65(1) = 415 350 + 65(2) = 480 350 + 65(3) = 545 Hours 0 1 2 3 Total cost 350 415 480 545

(Contd. ) Dance Rooms Here charges $65 per hour and a $350 deposit for renting a dance room. b. Graph the values from the table. Label the axes in the context of the problem. Hours 0 Total cost 350 1 415 2 3 480 545 Linear model: Graph forms a straight line; constant slope!

(Contd. ) Dance Rooms Here charges $65 per hour and a $350 deposit for renting a dance room. c. Express the total cost, C, of renting a dance room as a function of the number of hours, h. Total cost = deposit + rate per hour Total cost = 350 + 65 per hour Therefore, the linear function is: C(h) = 350 + 65 h (continued on the next slide)

(Contd. ) Dance Rooms Here charges $65 per hour and a $350 deposit for renting a dance room. d. Use your function to calculate the total cost for renting a dance room for 6. 5 hours. We will evaluate the function at h = 6. 5 C(6. 5) = 350 + 65(6. 5) = 350 + 422. 5 = 772. 50 The total cost for renting a dance room for 6. 5 hours is $772. 50. (continued on the next slide)

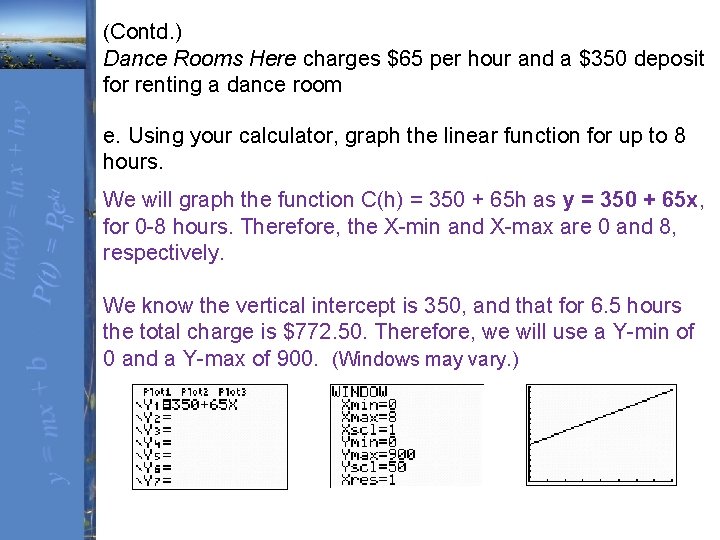
(Contd. ) Dance Rooms Here charges $65 per hour and a $350 deposit for renting a dance room e. Using your calculator, graph the linear function for up to 8 hours. We will graph the function C(h) = 350 + 65 h as y = 350 + 65 x, for 0 -8 hours. Therefore, the X-min and X-max are 0 and 8, respectively. We know the vertical intercept is 350, and that for 6. 5 hours the total charge is $772. 50. Therefore, we will use a Y-min of 0 and a Y-max of 900. (Windows may vary. )

Finding the Equation of a Linear Function • Slope-Intercept Form or Point-Slope Form. • Will need the slope and one point on the line. Note: See previous lessons to review these concepts: Slope, Rate of Change, Horizontal and Vertical Intercepts.

Slope-Intercept Form If we know the rate of change (slope), m, and the vertical intercept, (0, b), of a linear function, we can use the slope-intercept form, y = mx + b, to find the equation of the linear function. Point-Slope Form If we know the slope, m, and any point (x 1, y 1) on the line, we can use the point-slope form, y – y 1 = m(x – x 1) to find the equation of the linear function.

Find the equation of the line that passes through (0, – 3) and has slope – 2. The y-intercept is given: (0, – 3). Therefore, b = – 3. The slope is given: m = – 2. We are looking for y = mx + b, where m is the slope and b is the y-intercept. The linear equation is y = – 2 x – 3. We can corroborate with the graph:

Find the equation of the line that passes through (0, – 10) and (– 3, 28). We are looking for y = mx + b, where m is the slope and b is t y-intercept. The y-intercept is given: (0, – 10). Therefore, b = – 10 We can use the given points to find the slope, m: The linear function is:

During a tropical storm, Jerry’s air boat was flooded with 40 gallons of water. He had to remove the water with his onboard sump pump. The graph below depicts the amount of water G (in gallons), left in the boat after t minutes of using the sump pump. Find a formula for the function that describes the graph. The vertical intercept is given: (0, 40). Therefore, b = 40 We can use the intercepts, (25, 0) and (0, 40), to find the slope: The linear function is:

Find the equation of the line that passes through (– 5, 9) and has slope – 7. Find the y-intercept of this linear function. We do not know the value of the y-intercept, thus will use the point-slope form of the line, y – y 1 = m(x – x 1). Let m = – 7 and the given point (x 1, y 1) = (– 5, 9). We now substitute these values in the point-slope form of the line. y – 9 = – 7[x – (– 5)] y – 9 = – 7(x + 5) We can now distribute the – 7 and simplify to find the y-intercept: y – 9 = – 7 x – 35 y = – 7 x – 26 By simplifying, we converted the equation to slope-intercept form, and observe that the y-intercept is (0, – 26).

Write the slope-intercept form of the equation for the line passing through the points (– 7, 18. 3) and (3, 11. 2). First, find slope: Use the point-slope formula (with any of the given points), and simplify to slope-intercept form: y – y 1 = m(x – x 1) y – 11. 2 = – 0. 71(x – 3) y – 11. 2 = – 0. 71 x + 2. 13 y = – 0. 71 x + 2. 13 + 11. 2 y = – 0. 71 x – 13. 33

Finding the Equation of a Linear Function Summary Ø For both the slope-intercept form and the point-slope form of the linear function, you will need the slope. If the rate of change is not given and you know at least two points, you can calculate the slope. Ø When given the vertical intercept (y-intercept), it is simpler to use the slope-intercept form: y = mx + b. Ø When given a point that is not necessarily the vertical intercept, use the point-slope form: y – y 1 = m(x – x 1).

Equations of Horizontal and Vertical Lines Horizontal Line: y = b, where b is a constant. The line intersects the y-axis at (0, b). Recall that the slope of a horizontal line is 0. Example: y = 3 Vertical Line: x = a where a is a constant. The line intersects the x-axis at (a, 0). Recall that the slope of a vertical line is undefined. Example: x = 3

The equation of the vertical line that passes through (2, – 5) is x = 2. a. True b. False The x-coordinate of (2, – 5) is 2. Therefore, the vertical line through this point has equation x = 2. Answer: a

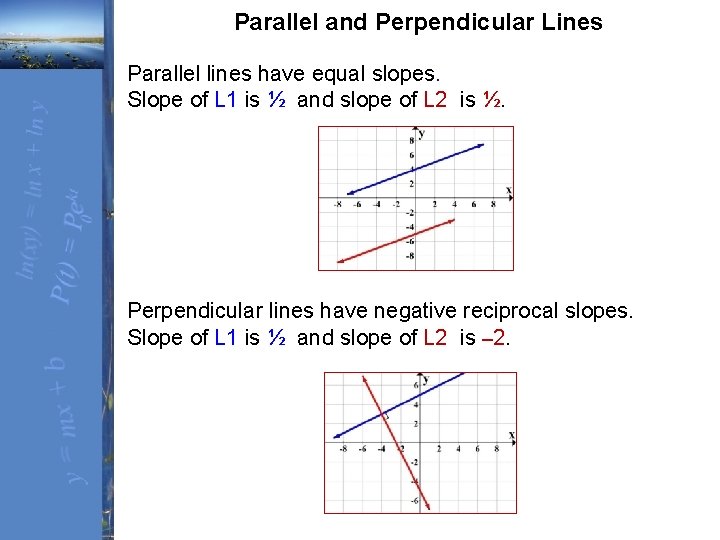
Parallel and Perpendicular Lines Parallel lines have equal slopes. Slope of L 1 is ½ and slope of L 2 is ½. Perpendicular lines have negative reciprocal slopes. Slope of L 1 is ½ and slope of L 2 is – 2.

Find the slope-intercept form of the equation of the line through the point (2, – 3), parallel to the line y = 5 x + 3. Parallel lines have equal slopes. So, find a line with slope m = 5 and passing through (2, – 3). y – y 1 = m(x – x 1) y – (– 3) = 5(x – 2) y + 3 = 5 x – 10 y = 5 x – 13

Find the point-slope form of the equation of the line through the point (– 2, 3), parallel to the line 6 x + 3 y – 9 = 0. ? First, change 6 x + 3 y – 9 = 0 to slope-intercept form: 3 y = – 6 x + 9 y = – 2 x + 3 Now, find a line with slope m = – 2 and passing through (– 2, 3). y – y 1 = m(x – x 1) y – 3 = – 2[x – (– 2)] y – 3 = – 2(x + 2) Stop here! (Asked for point-slope form of the line. )

Find the slope-intercept form of the equation of the line through the point (– 2, 3) perpendicular to the line 6 x + 3 y – 9 = 0. ? First, change 6 x + 3 y – 9 = 0 to slope-intercept form: 3 y = – 6 x + 9 y = – 2 x + 3 Now, find a line with slope m = ½ and passing through (– 2, 3). y – y 1 = m(x – x 1) y – 3 = ½ [x – (– 2)] y – 3 = ½ x + 1 y = ½ x + 4

Using your textbook, practice the problems assigned by your instructor to review the concepts from Section 1. 5.