Root Locus Techniques DNT 354 CONTROL PRINCIPLE Date

Root Locus Techniques DNT 354 - CONTROL PRINCIPLE Date: 2/09/2015 Prepared by: Nor Shaifudin Bin Abdul Hamid Email: norshaifudin@unimap. edu. my

CONTENTS Introduction The Control System Problem Complex Numbers as Vector Defining Root Locus

INTRODUCTION Root locus is a graphical representation of the closed-loop poles as a system parameter is varied. Provides a qualitative description of systems performance. The advantage of this technique is in its ability to provide solution for systems of order higher than two. Also provide a graphical representation of system’s stability. i. iii. Ranges of stability Ranges of instability Conditions that cause a system to break into oscillation Two concepts that will be reviewed beforehand: i. ii. Control system problem Complex numbers and representation as vectors

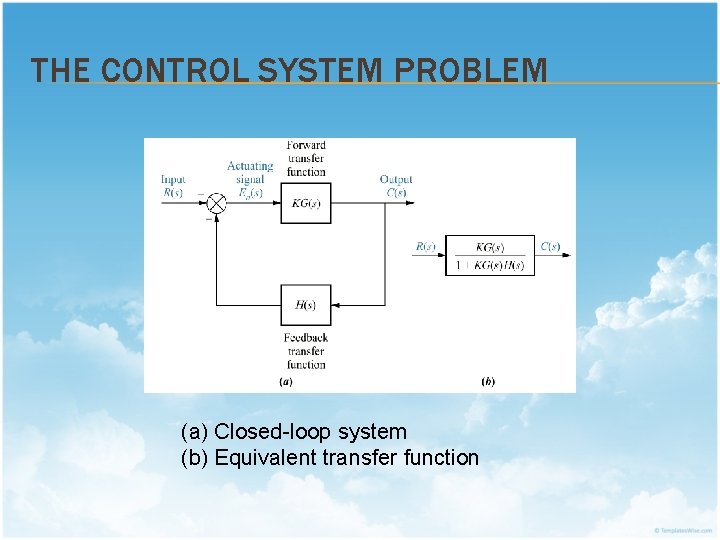
THE CONTROL SYSTEM PROBLEM Poles of open-loop transfer function: i. ii. Poles of closed-loop transfer function: i. ii. Easy to obtain via inspection of the denominator Not affected by changes in system gain More difficult to obtain which needs factorization of closedloop system characteristic polynomial Affected by changes in system gain With KG(s) as the forward transfer function and H(s) as the feedback transfer function, the closed-loop transfer function T(s) are reduced to:

THE CONTROL SYSTEM PROBLEM (a) Closed-loop system (b) Equivalent transfer function

THE CONTROL SYSTEM PROBLEM Letting, Then, If given, Poles of G(s) = -2, 0 Zeros of G(s) = -1 Then, Poles of H(s) = -4 Zeros of H(s) = -3

THE CONTROL SYSTEM PROBLEM It is observed: i. ii. The zeros of T(s) consist of the zeros of G(s) and the poles of H(s). The poles of T(s) are not immediately known without factoring the denominator and are a function of K. Since the system’s transient response and stability are dependant upon the poles of T(s), root locus enables monitoring of the poles as the parameter K is varied.

COMPLEX NUMBERS AS VECTOR Any complex number, σ + jω, described in Cartesian coordinates can be graphically represented by a vector. (a) s = + j (b) F(s) = s + a (c) Alternate representation of F(s) = s + a (d) F(s) = s + 7|s 5 + j 2

COMPLEX NUMBERS AS VECTOR It can be concluded that (s + a) is a complex number and can be represented by a vector drawn from the zero of the function to the point s. The complex number can also be represented in polar form with magnitude M and angle θ. Exercise: Plot and convert the following complex number into polar form. i. iii. s = 3 + j 4 s = -3 + j 5 s = -2 – j 7

COMPLEX NUMBERS AS VECTOR Assume a function, Where, Π : Product m : Number of zeros n : Number of poles Each factor in the numerator and denominator is a complex number that can be represented as a vector. The function defines the complex arithmetic to be performed to evaluate F(s) at any point, s.

COMPLEX NUMBERS AS VECTOR Since each complex factor can be thought of as a vector, the magnitude M, of F(s) at any point s is, Where, • │(s + zi)│ is magnitude of the vector drawn from the zero of F(s) at –zi to the point s. • │(s + pj)│ is magnitude of the vector drawn from the pole of F(s) at –pj to the point s.

COMPLEX NUMBERS AS VECTOR The angle θ, of F(s) at any point s is, Where, • Zero angle is the angle measured from the positive extension of the real axis, of a vector drawn from the zero of F(s) at –zi to point s. • Pole angle is the angle measured from the positive extension of the real axis, of a vector drawn from the pole of F(s) at –pj to point s.

COMPLEX NUMBERS AS VECTOR Example: Find F(s) at the point s = -3 + j 4. Vector originating at zero at -1 Vector originating at pole at the origin Vector originating at pole at -2

COMPLEX NUMBERS AS VECTOR Example: Find F(s) at the point s = -3 + j 4. The result for evaluating F(s) at the point -3 + j 4

COMPLEX NUMBERS AS VECTOR Example: Find F(s) at the point s = -7 + j 9 using the following ways. a) b) Directly substituting the point into F(s). Calculating the result using vectors. Answer:

DEFINING ROOT LOCUS Root locus are used to analyze and design the effect of loop gain upon the system’s transient response and stability. By taking the Camera. Man system as an example, the video camera system are designed to automatically follow the subject. The tracking system consists of a dual sensor and a transmitter, where one component is mounted on the camera, and the other worn by the subject. An imbalance between the outputs of the two sensors receiving energy from the transmitted causes the system to rotate the camera to balance out the difference and seek the source of energy.

DEFINING ROOT LOCUS (a) Camera. Man® Presenter Camera System automatically follows a subject who wears infrared sensors on their front and back tracking commands and audio are relayed to Camera. Man via a radio frequency link from a unit worn by the subject. (b) Block diagram (c) Closed-loop transfer function

DEFINING ROOT LOCUS Pole location as a function of gain for the Camera. Man system.

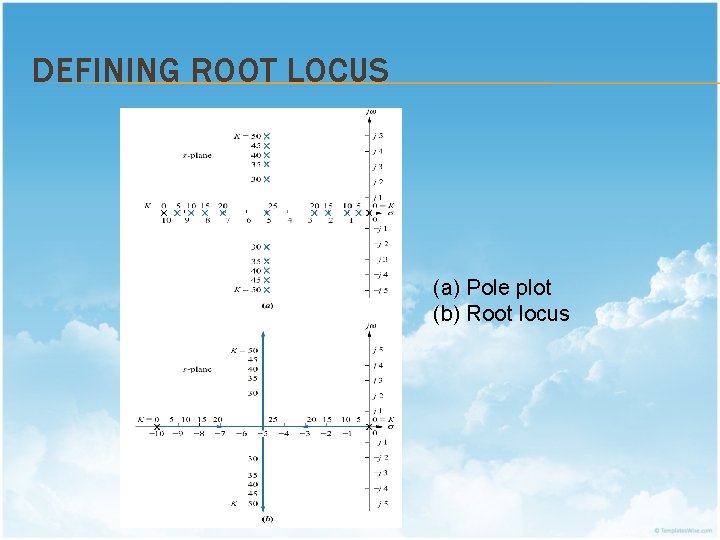
DEFINING ROOT LOCUS (a) Pole plot (b) Root locus

DEFINING ROOT LOCUS It is observed: i. ii. iv. At K = 0, poles exists at -10 and 0. As K increases, both poles move towards each other and meet at -5. The poles break away into the complex plane as K increases further. One pole moves upward while the other downwards. The individual closed-loop poles plotted are removed and replaced with solid lines. Thus, root locus is a representation of the paths of the closed-loop poles as the gain is varied.

DEFINING ROOT LOCUS With regards to transient response: i. iii. With regards to the underdamped portion of the root locus i. iii. The poles are real for gains less than 25. Thus, the system is overdamped. At a gain of 25, the poles are real and repeated. Thus, the system is critically damped. As gain increases above 25, the poles are complex conjugate. Thus, the system is underdamped. The settling time remains the same. Damping ratio diminishes and percent overshoot increases. Damped frequency of oscillation increases. With regards to stability, the system is always stable because the root locus never crosses into the RHP.