MANE 4240 CIVL 4240 Introduction to Finite Elements

MANE 4240 & CIVL 4240 Introduction to Finite Elements Prof. Suvranu De FEM Discretization of 2 D Elasticity

Reading assignment: Lecture notes Summary: • FEM Formulation of 2 D elasticity (plane stress/strain) • Displacement approximation • Strain and stress approximation • Derivation of element stiffness matrix and nodal load vector • Assembling the global stiffness matrix • Application of boundary conditions • Physical interpretation of the stiffness matrix

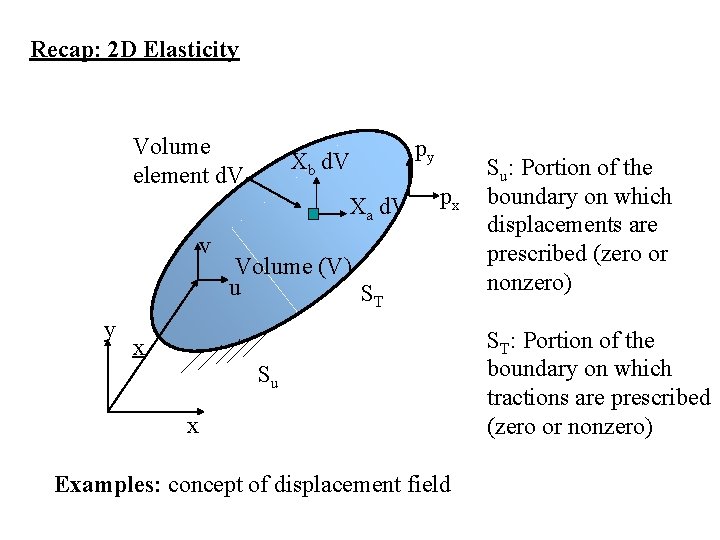
Recap: 2 D Elasticity Volume element d. V Xb d. V Xa d. V v y py px Volume (V) u ST x Su x Examples: concept of displacement field Su: Portion of the boundary on which displacements are prescribed (zero or nonzero) ST: Portion of the boundary on which tractions are prescribed (zero or nonzero)

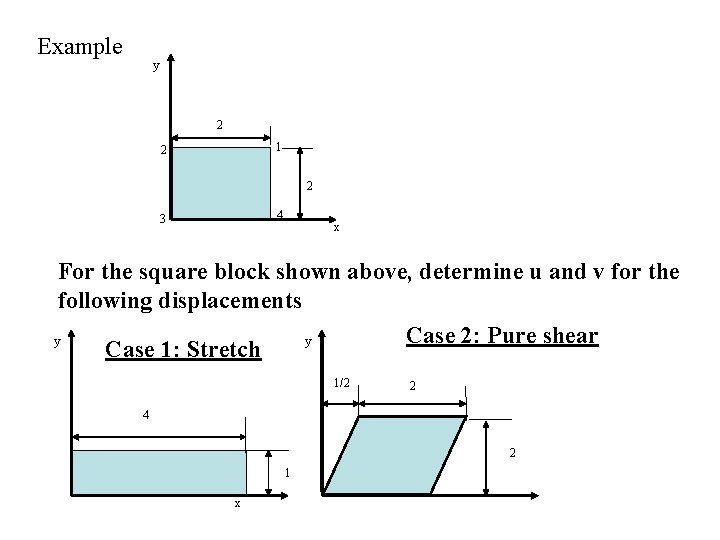
Example y 2 1 2 2 4 3 x For the square block shown above, determine u and v for the following displacements Case 2: Pure shear y y Case 1: Stretch 1/2 2 4 2 1 x

Solution Case 1: Stretch Check that the new coordinates (in the deformed configuration) Case 2: Pure shear Check that the new coordinates (in the deformed configuration)

Recap: 2 D Elasticity For plane stress (3 nonzero stress components) For plane strain (3 nonzero strain components)

Strong formulation Equilibrium equations Boundary conditions 1. Displacement boundary conditions: Displacements are specified on portion Su of the boundary 2. Traction (force) boundary conditions: Tractions are specified on portion ST of the boundary Now, how do I express this mathematically? But in finite element analysis we DO NOT work with the strong formulation (why? ), instead we use an equivalent Principle of Minimum Potential Energy

Principle of Minimum Potential Energy (2 D) Definition: For a linear elastic body subjected to body forces X=[Xa, Xb]T and surface tractions TS=[px, py]T, causing displacements u=[u, v]T and strains e and stresses s, the potential energy P is defined as the strain energy minus the potential energy of the loads (X and TS) P=U-W

Volume element d. V Xb d. V Xa d. V v y Volume (V) u ST x Su x py px

Strain energy of the elastic body Using the stress-strain law In 2 D plane stress/plane strain

Principle of minimum potential energy: Among all admissible displacement fields the one that satisfies the equilibrium equations also render the potential energy P a minimum. “admissible displacement field”: 1. first derivative of the displacement components exist 2. satisfies the boundary conditions on Su

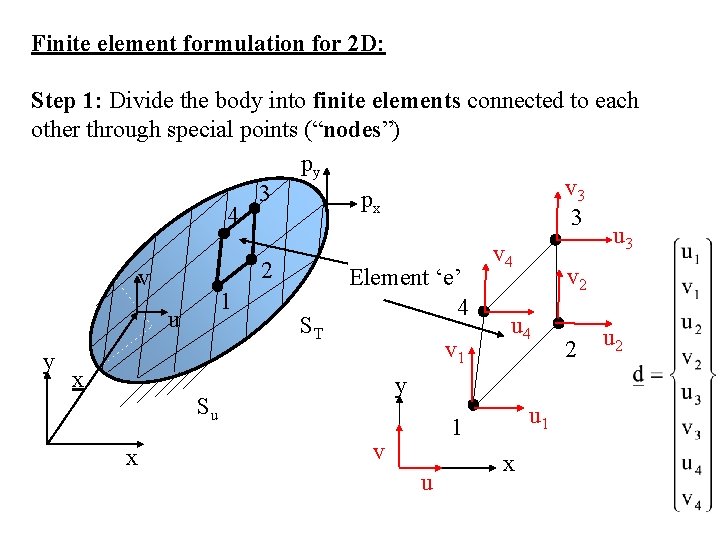
Finite element formulation for 2 D: Step 1: Divide the body into finite elements connected to each other through special points (“nodes”) py v 3 3 px 4 3 u 3 v 4 2 v 2 Element ‘e’ v 1 4 u u 4 ST u 2 v 1 2 y x y Su u 1 1 x v u x

Total potential energy Potential energy of element ‘e’: This term may or may not be present depending on whether the element is actually on ST Total potential energy = sum of potential energies of the elements

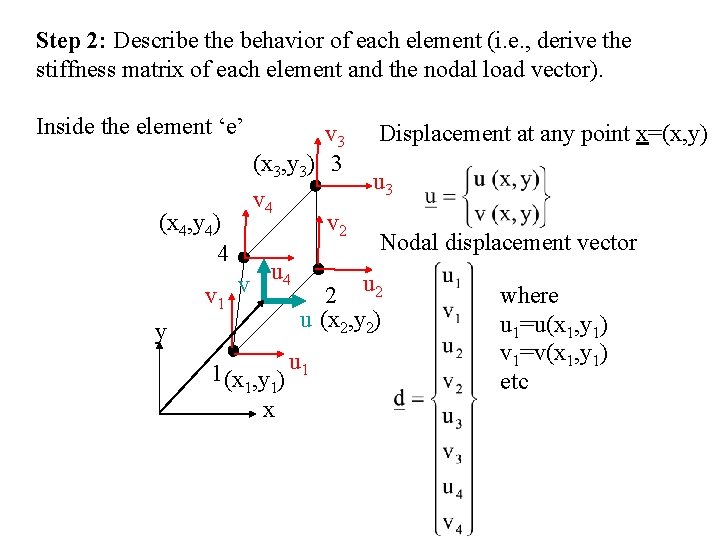
Step 2: Describe the behavior of each element (i. e. , derive the stiffness matrix of each element and the nodal load vector). Inside the element ‘e’ (x 4, y 4) 4 v 1 v y v 3 (x 3, y 3) 3 v 4 v 2 u 4 Displacement at any point x=(x, y) u 3 Nodal displacement vector 2 u (x 2, y 2) 1(x 1, y 1) u 1 x where u 1=u(x 1, y 1) v 1=v(x 1, y 1) etc

Recall If we knew u then we could compute the strains and stresses within the element. But I DO NOT KNOW u!! Hence we need to approximate u first (using shape functions) and then obtain the approximations for e and s (recall the case of a 1 D bar)

TASK 1: APPROXIMATE THE DISPLACEMENTS WITHIN EACH ELEMENT Displacement approximation in terms of shape functions TASK 2: APPROXIMATE THE STRAIN and STRESS WITHIN EACH ELEMENT Strain approximation Stress approximation TASK 3: DERIVE THE STIFFNESS MATRIX OF EACH ELEMENT USING THE PRINCIPLE OF MIN. POT ENERGY We’ll see these for a generic element in 2 D today and then derive expressions for specific finite elements in the next few classes

TASK 1: APPROXIMATE THE DISPLACEMENTS WITHIN EACH ELEMENT v Displacement approximation in terms of shape functions v 3 3 u 3 v 4 v 2 Displacement approximation within element ‘e’ 4 u 2 v 1 2 y u 1 1 u x

We’ll derive specific expressions of the shape functions for different finite elements later

TASK 2: APPROXIMATE THE STRAIN and STRESS WITHIN EACH ELEMENT Approximation of the strain in element ‘e’

Compact approach to derive the B matrix:

Stress approximation within the element ‘e’

TASK 3: DERIVE THE STIFFNESS MATRIX OF EACH ELEMENT USING THE PRINCIPLE OF MININUM POTENTIAL ENERGY Potential energy of element ‘e’: Lets plug in the approximations

Rearranging From the Principle of Minimum Potential Energy Discrete equilibrium equation for element ‘e’

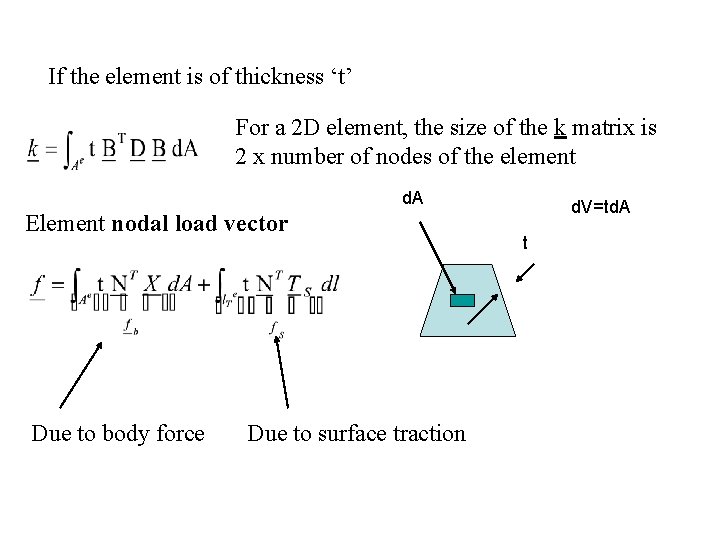
Element stiffness matrix for element ‘e’ For a 2 D element, the size of the k matrix is 2 x number of nodes of the element Question: If there are ‘n’ nodes per element, then what is the size of the stiffness matrix of that element? Element nodal load vector ST e e Due to body force Due to surface traction

If the element is of thickness ‘t’ For a 2 D element, the size of the k matrix is 2 x number of nodes of the element d. A Element nodal load vector Due to body force Due to surface traction d. V=td. A t

The properties of the element stiffness matrix 1. The element stiffness matrix is singular and is therefore noninvertible 2. The stiffness matrix is symmetric 3. Sum of any row (or column) of the stiffness matrix is zero! (why? )

Computation of the terms in the stiffness matrix of 2 D elements v 4 4 v 3 u 4 The B-matrix (strain-displacement) corresponding to this element is 3 u 3 v y v 1 (x, y) v 2 u 2 1 u 2 u 1 v 1 u 2 v 2 u 3 x We will denote the columns of the B-matrix as v 3 u 4 v 4

The stiffness matrix corresponding to this element is which has the following form u 1 v 1 u 2 v 2 u 3 v 3 u 4 v 4 The individual entries of the stiffness matrix may be computed as follows

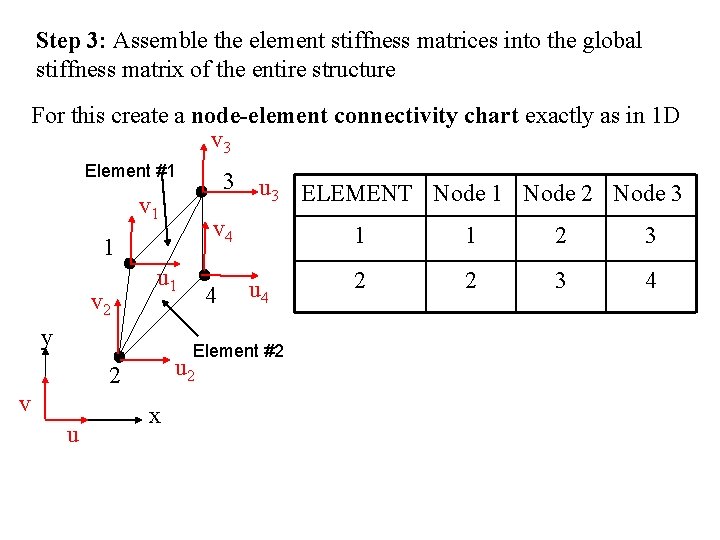
Step 3: Assemble the element stiffness matrices into the global stiffness matrix of the entire structure For this create a node-element connectivity chart exactly as in 1 D v 3 Element #1 3 v 1 v 4 1 v 2 u 1 y u 3 ELEMENT Node 1 Node 2 Node 3 4 u 4 Element #2 u 2 2 v u x 1 1 2 3 2 2 3 4

Stiffness matrix of element 1 u 1 v 1 u 2 v 2 u 3 v 3 u 1 Stiffness matrix of element 2 u 2 v 2 u 3 v 3 u 4 v 4 u 2 v 1 u 2 v 2 u 3 v 3 u 4 v 4 There are 6 degrees of freedom (dof) per element (2 per node)

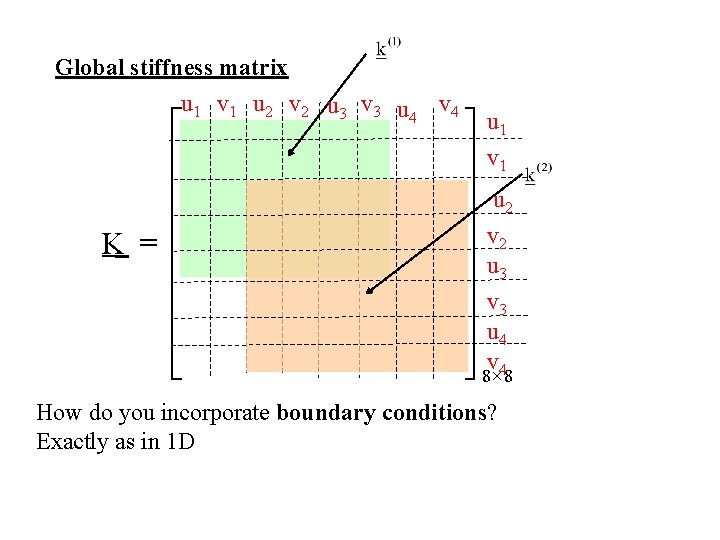
Global stiffness matrix u 1 v 1 u 2 v 2 u 3 v 3 u 4 v 4 é ê ê ê K = ê ê êë ù u 1 ú v 1 ú u ú 2 v 2 ú ú u 3 ú v 3 ú u 4 úû 8 v´ 48 How do you incorporate boundary conditions? Exactly as in 1 D

Finally, solve the system equations taking care of the displacement boundary conditions.

Physical interpretation of the stiffness matrix Consider a single triangular element. The six corresponding equilibrium equations ( 2 equilibrium equations in the x- and ydirections at each node times the number of nodes) can be written symbolically as v 1 1 y u 1 v 2 v 3 3 u 2 2 x u 3

Choose u 1 = 1 and rest of the nodal displacements = 0 u 1=1 1 3 y 2 x Hence, the first column of the stiffness matrix represents the nodal loads when u 1=1 and all other dofs are fixed. This is the physical interpretation of the first column of the stiffness matrix. Similar interpretations exist for the other columns

= “Force” at d. o. f ‘i’ due to unit displacement at d. o. f ‘j’ keeping all the other d. o. fs fixed Now consider the ith row of the matrix equation This is the equation of equilibrium at the ith dof

Consistent and Lumped nodal loads Recall that the nodal loads due to body forces and surface tractions These are known as “consistent nodal loads” 1. They are derived in a consistent manner using the Principle of Minimum Potential Energy 2. The same shape functions used in the computation of the stiffness matrix are employed to compute these vectors

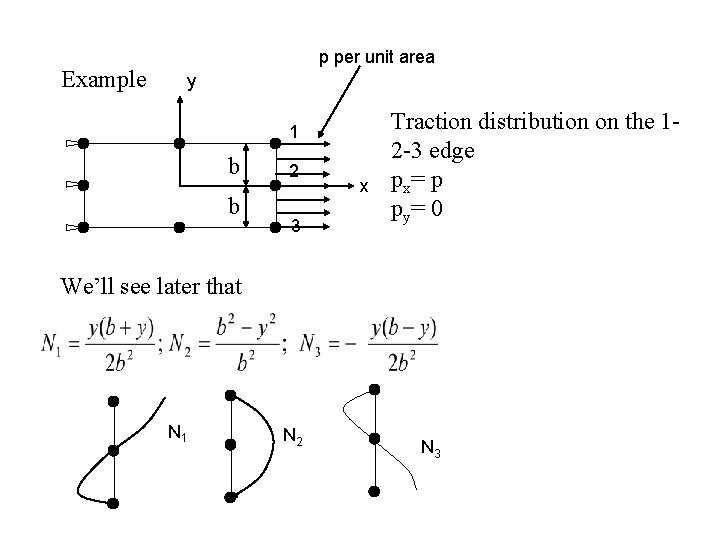
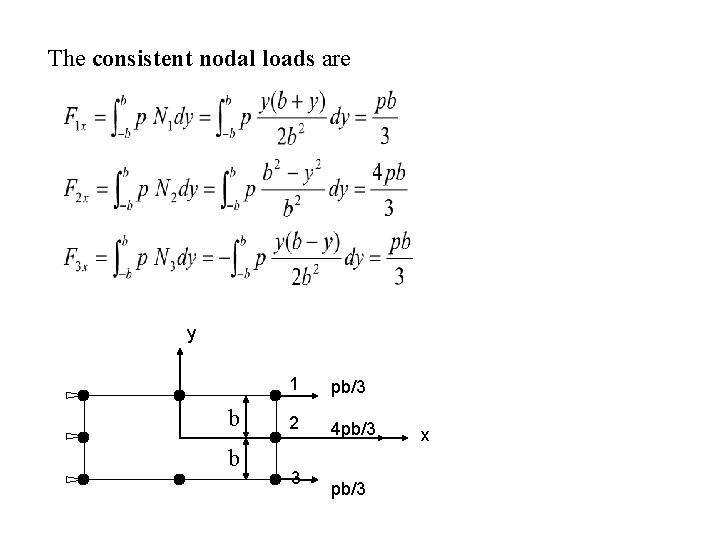
Example p per unit area y 1 b b 2 3 x Traction distribution on the 12 -3 edge px= p py= 0 We’ll see later that N 1 N 2 N 3

The consistent nodal loads are y b b 1 pb/3 2 4 pb/3 3 pb/3 x

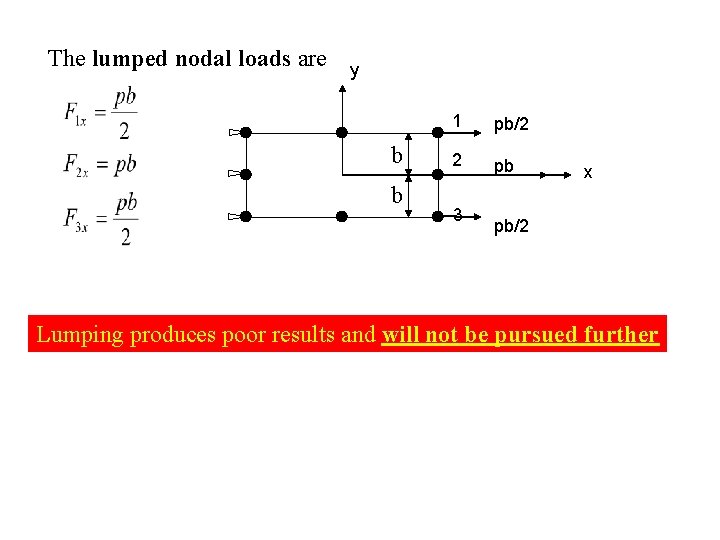
The lumped nodal loads are y b b 1 pb/2 2 pb 3 x pb/2 Lumping produces poor results and will not be pursued further

Summary: For each element Displacement approximation in terms of shape functions Strain approximation in terms of strain-displacement matrix Stress approximation Element stiffness matrix Element nodal load vector