MANE 4240 CIVL 4240 Introduction to Finite Elements

MANE 4240 & CIVL 4240 Introduction to Finite Elements Prof. Suvranu De Convergence of analysis results

Reading assignment: Lecture notes Summary: • Concept of convergence • Criteria for monotonic convergence : completeness (rigid body modes + constant strain) + compatibility • Incompatible elements and the patch test • Rate of convergence

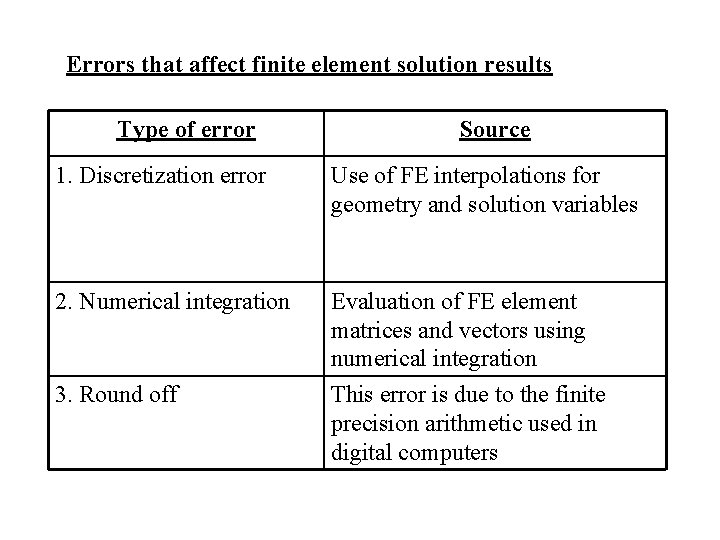
Errors that affect finite element solution results Type of error Source 1. Discretization error Use of FE interpolations for geometry and solution variables 2. Numerical integration Evaluation of FE element matrices and vectors using numerical integration 3. Round off This error is due to the finite precision arithmetic used in digital computers

What is “convergence”? Physical system Mathematical model FE model “Convergence” of FE solution results to the exact solution of the mathematical model FE scheme exhibits convergence if the Discretization error → 0 as the mesh is made infinitely fine (i. e. , element size → 0)

Mesh refinement h-refinement p-refinement h=element size p=polynomial order

Convergence in energy and displacement u : exact displacement solution to a problem that makes the potential energy of the system a minimum corresponding stress and strain Exact strain energy of the body uh : FE solution (‘h’ refers to the element size) corresponding stress and strain Approximate strain energy of the body

Calculation of strain energies Example: Consider a linear elastic bar with varying cross section 2 1 x 80 cm P=3 E/80 E: Young’s modulus Boundary conditions Analytical solution The governing differential (equilibrium) equation Eq(1)

The exact strain energy of the system is If we discretize the problem using a single linear finite element, the stiffness matrix is The strain energy of the FE system is Note

Convergence in strain energy Monotonic convergence Nonmonotonic convergence

Convergence in displacement Monotonic convergence Nonmonotonic convergence

Criteria for monotonic convergence 1. COMPLETENESS 2. COMPATIBILITY © 2002 Brooks/Cole Publishing / Thomson Learning™

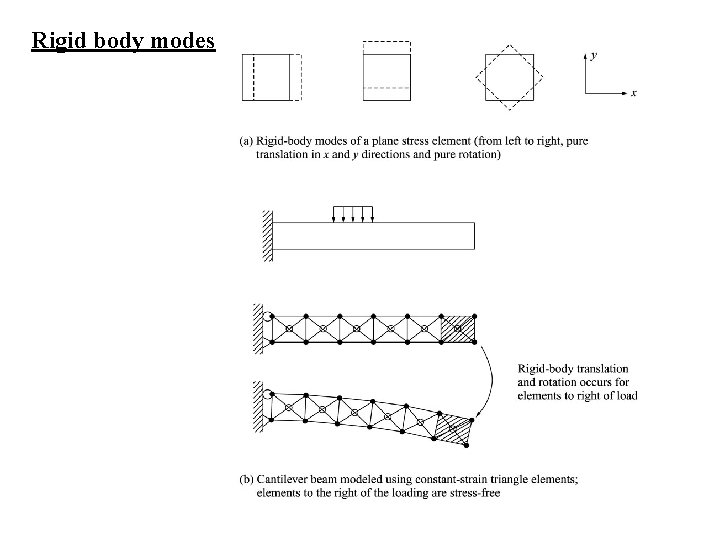
CONDITION 1. COMPLETENESS This requires that the displacement interpolation functions must be chosen so that the elements can represent 1. Rigid body modes 2. Constant strain states

Rigid body modes

The # of rigid body modes of an element = # of zero eigenvalues of the element stiffness matrix

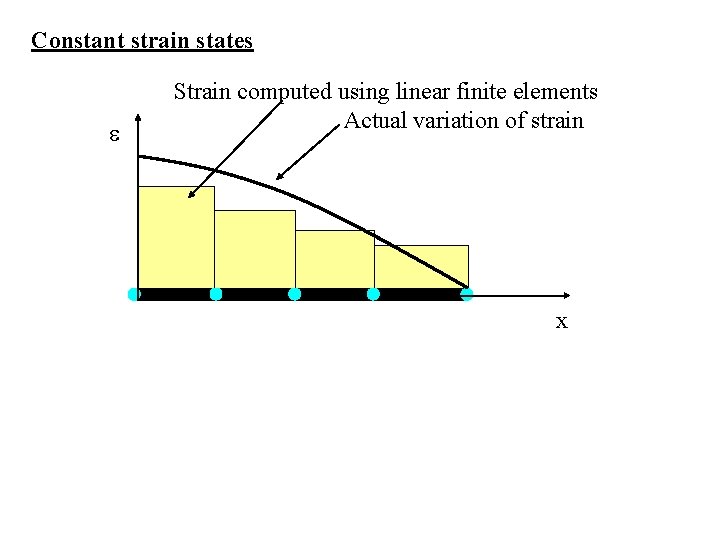
Constant strain states e Strain computed using linear finite elements Actual variation of strain x

Mathematical implication of the two conditions (rigid body modes + constant strain state) Inside a finite element (of any order) in 1 D but this is just a polynomial… Hence The requirement for completeness in 1 D is that the displacement approximation be at least a linear polynomial of degree (k=1), ie any 2 node element and higher is complete

Mathematical implication of the two conditions (rigid body modes + constant strain state) Inside a finite element (of any order) in 2 D but this is just a polynomial… Hence The requirement for completeness in 1 D is that the displacement approximation be at least a linear polynomial of degree (k=1).

Mathematical implication of the two conditions (rigid body modes + constant strain state) The element displacement approximation must be at least a COMPLETE polynomial of degree one k=1 1 D 2 D

In 2 D, the minimum displacement assumption needs to be Translation along x Translation along y Rigid body rotation about z-axis

CONDITION 2. COMPATIBILITY The assumed displacement variations are continuous within elements and across inter-element boundaries Ensures that strains are bounded within elements and across element boundaries. If ‘u’ is discontinuous across element boundaries then the strains blow up in-between elements and this leads to erroneous contributions to the potential energy of the structure Physical meaning: no gaps/cracks open up when the finite element assemblage is loaded

Nonconforming elements and the patch test Conforming = compatible Nonconforming = incompatible Ideal: Conforming elements Observation: Certain nonconforming elements also give good results, at the expense of nonmonotonic convergence Nonconforming elements: • satisfy completeness • do not satisfy compatibility • result in at least nonmonotonic convergence if the element assemblage as a whole is complete, i. e. , they satisfy the PATCH TEST

PATCH TEST: 1. A patch of elements is subjected to the minimum displacement boundary conditions to eliminate all rigid body motions 2. Apply to boundary nodal points forces or displacements which should result in a state of constant stress within the assemblage 3. Nodes not on the boundary are neither loaded nor restrained. 4. Compute the displacements of nodes which do not have a prescribed value 5. Compute the stresses and strains The patch test is passed if the computed stresses and strains match the expected values to the limit of computer precision.

NOTES: 1. This is a great way to debug a computer code 2. Conforming elements ALWAYS pass the patch test 3. Nodes not on the boundary are neither loaded nor restrained. 4. Since a patch may also consist of a single element, this test may be used to check the completeness of a single element 5. The number of constant stress states in a patch test depends on the actual number of constant stress states in the mathematical model (3 for plane stress analysis. 6 for a full 3 D analysis)

CONVERGENCE RATE This is a measure of how fast the discretization error goes to zero a the mesh is refined Convergence rate depends on the order of the complete polynomial (k) used in the displacement approximation k=1 k=2 k=3

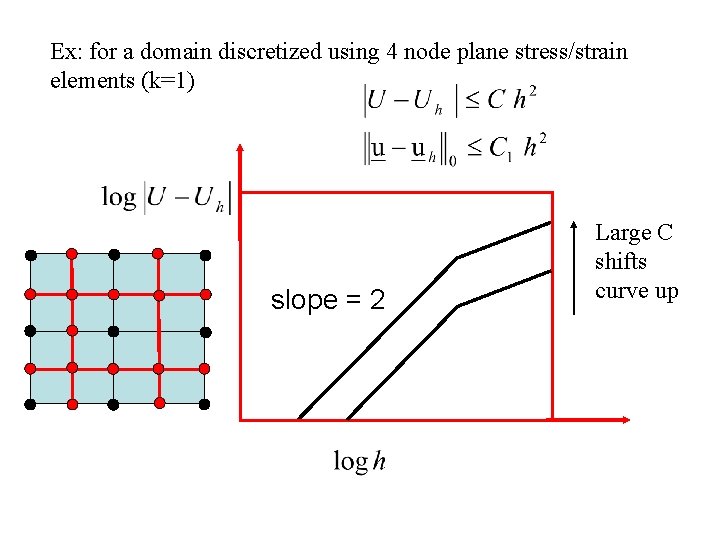
It can be shown that for (1) a sufficiently refined mesh and (2) for problems whose analytical solution does not contain singularities Convergence in strain energy : order 2 k Convergence in displacements : order p=k+1 C and C 1 are constants independent of ‘h’ but dependent on 1. the analytical solution 2. material properties 3. type of element used

Ex: for a domain discretized using 4 node plane stress/strain elements (k=1) slope = 2 Large C shifts curve up

Important property of finite element solution: When the conditions of monotonic convergence are satisfied (compatibility and completeness) the finite element strain energy always underestimates the strain energy of the actual structure Strain energy of mathematical model Strain energy of FE model