Logic Programming and MDPs for Planning Alborz Geramifard

Logic Programming and MDPs for Planning Alborz Geramifard Winter 2009

Index Introduction Logic Programming MDP+ Logic + Programming 2

Why do we care about planning? 3

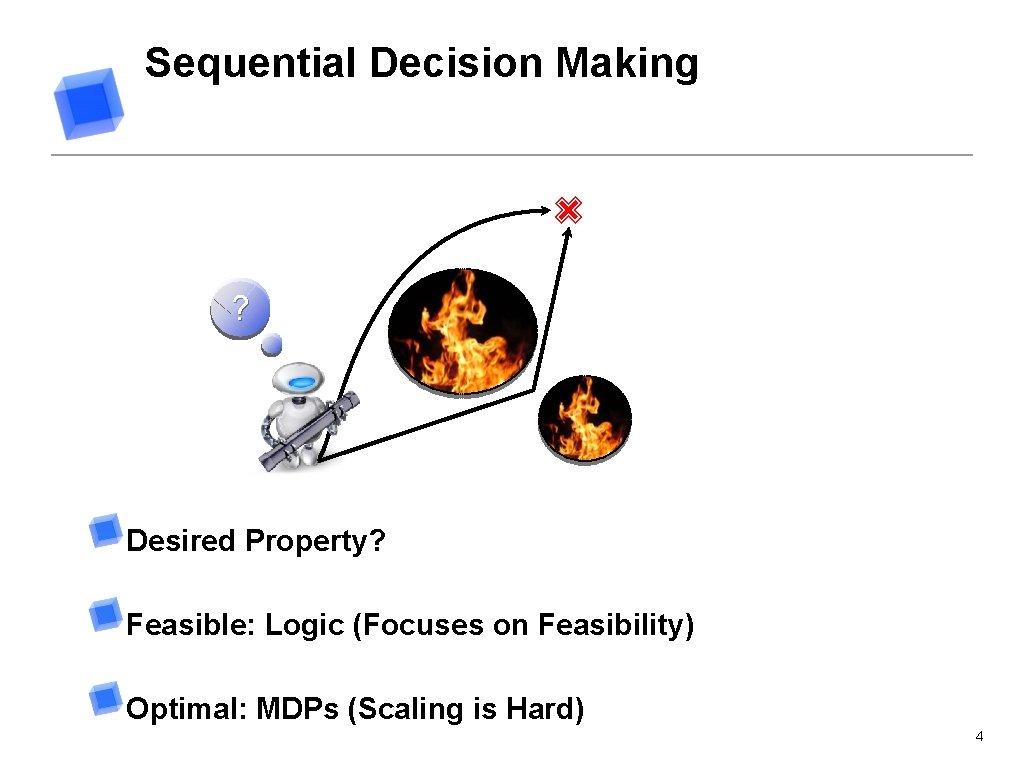
Sequential Decision Making ✙ ? Desired Property? Feasible: Logic (Focuses on Feasibility) Optimal: MDPs (Scaling is Hard) 4

Index Introduction Logic Programming MDP+ Logic + Programming 5

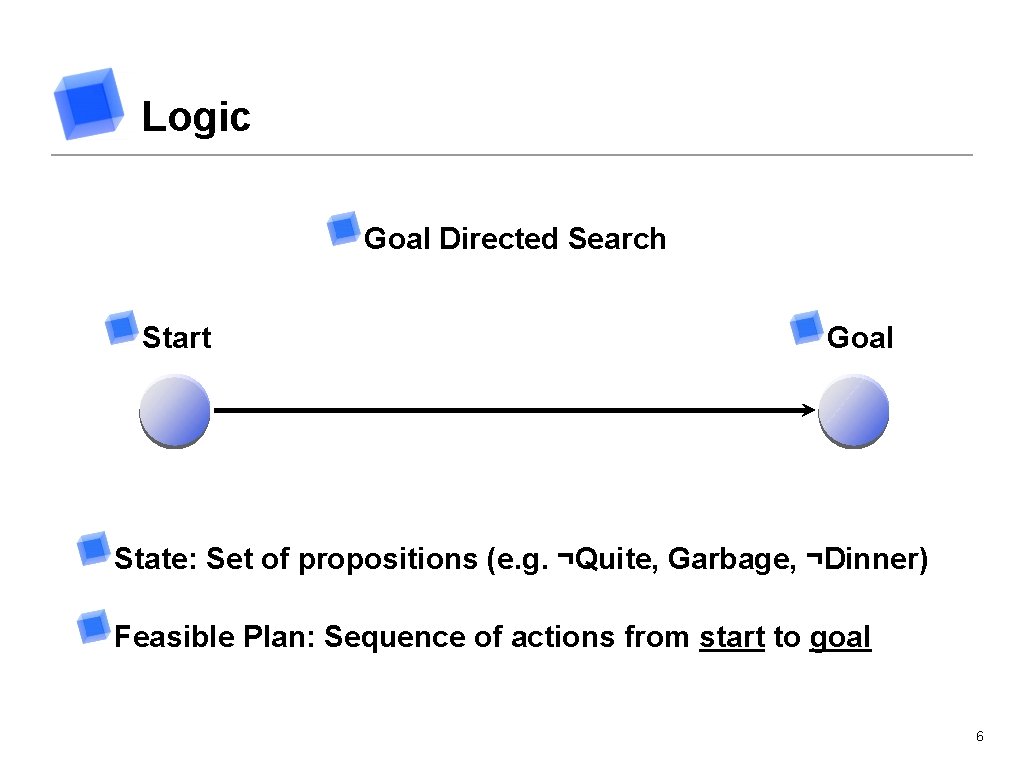
Logic Goal Directed Search Start Goal State: Set of propositions (e. g. ¬Quite, Garbage, ¬Dinner) Feasible Plan: Sequence of actions from start to goal 6

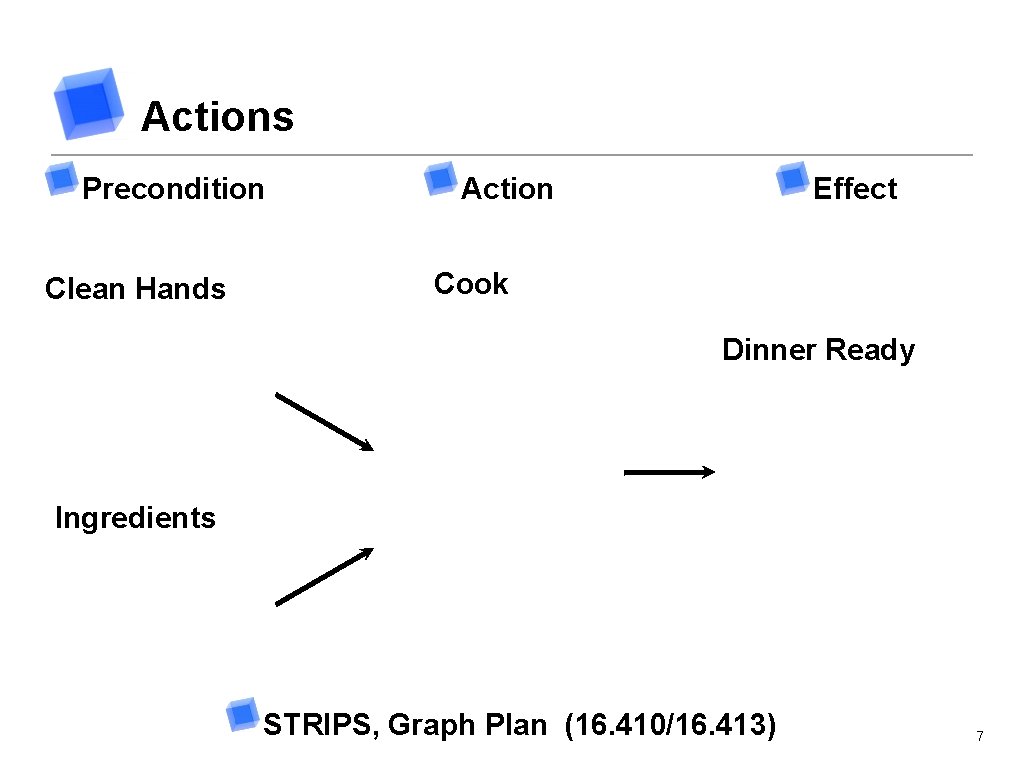
Actions Precondition Clean Hands Action Effect Cook Dinner Ready Ingredients STRIPS, Graph Plan (16. 410/16. 413) 7

Logic Programming Graph Plan or Forward Search Not easily scalable GOLOG: ALGOL in LOGIC[Levesque, et. al. 97] Restrict action space with programs Scales easier Results are dependent on high-level programs 8

Situation Calculus (Temporal Logic) Situation: S 0, do(A, S) Example: do(putdown(A), do(walk(L), do(pickup(A), S 0))) Relational Fluent: relations with values depending on situations Example: is_carrying(robot, p, s) Functional Fluent: situation dependent functions Example: loc(robot, s) More expressive than LTL 9

GOLOG: Syntax [Scott Sanner - ICAPS 08 Tutorial] ? Aren’t we hard-coding the whole solution? 10

Blocks World Actions: pickup(b), put. On. Table(b), put. On(b 1, b 2) Fluents: on. Table(b, s), on(b 1, b 2, s) GOLOG Program: while (∃b) ¬on. Table(b) then (pickup(b), put. On. Table(b)) end. While ? What does it do? 11

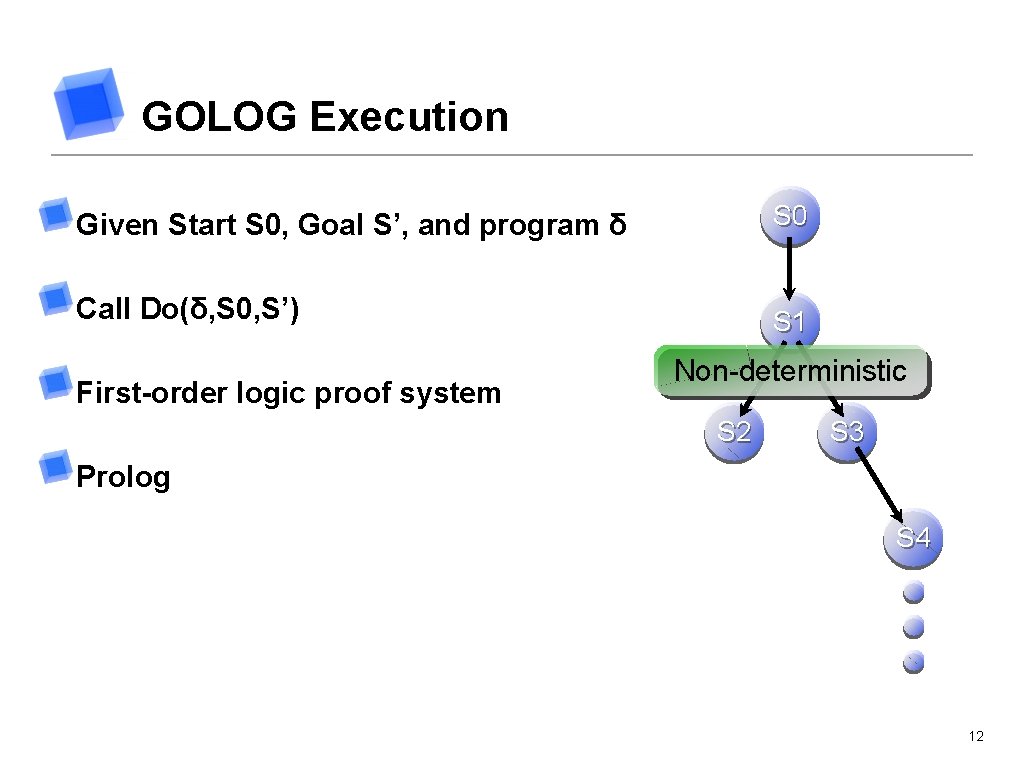
GOLOG Execution Given Start S 0, Goal S’, and program δ S 0 Call Do(δ, S 0, S’) S 1 First-order logic proof system Non-deterministic S 2 S 3 Prolog S 4 12

Index Introduction Logic Programming MDP+ Logic + Programming 13

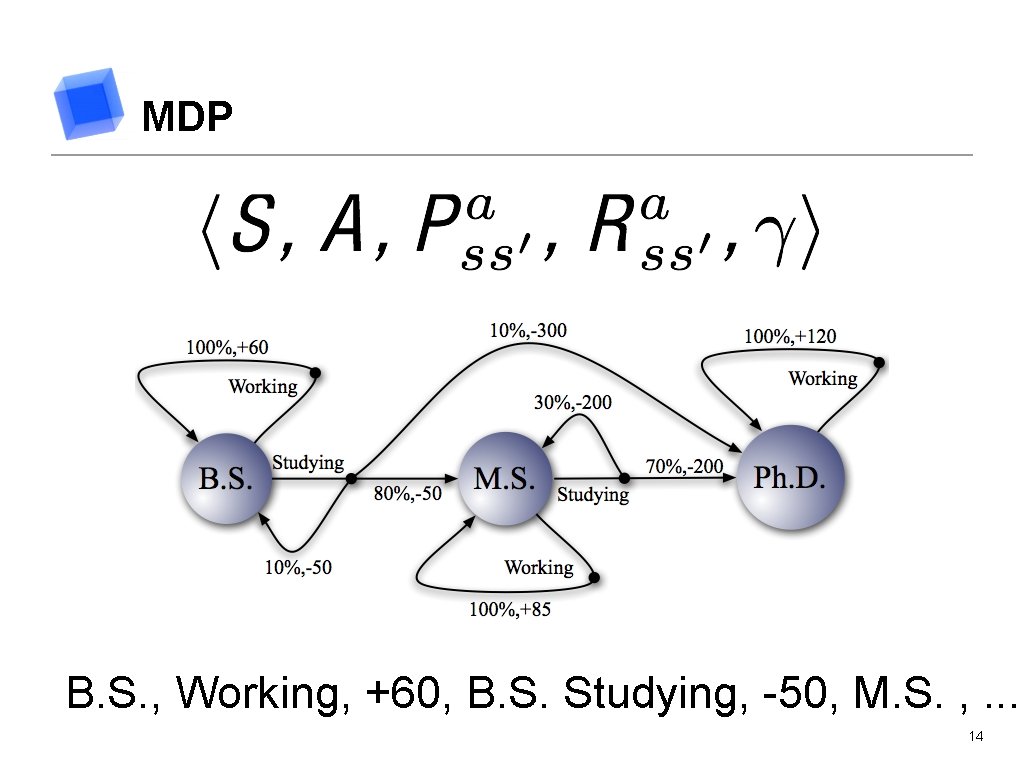
MDP B. S. , Working, +60, B. S. Studying, -50, M. S. , . . . 14

MDP Policy π(s): How to act in each state Value Function V(s): How good is it to be in each state? 15

MDP Goal Find the optimal policy (π*), which maximizes the value function for all states 16

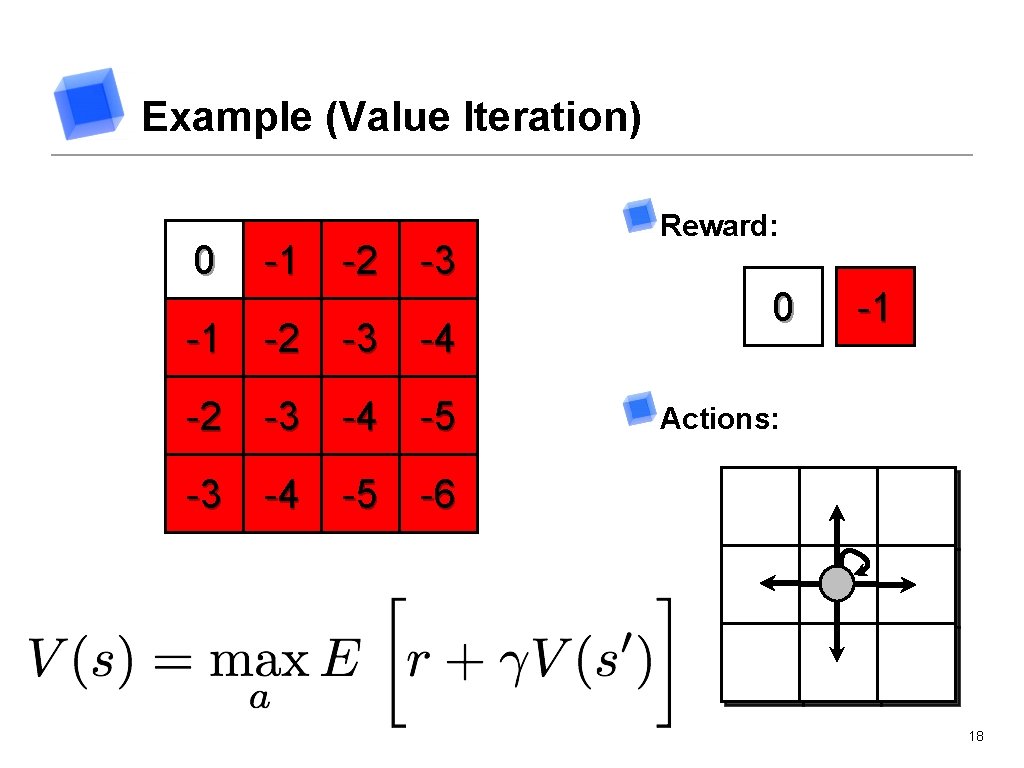
Example (Value Iteration) 0 -1 -2 0 -3 -1 -2 0 -4 -1 -2 0 -5 -1 -2 0 -6 -1 -2 0 Reward: 0 -1 Actions: 18

Index Introduction Logic Programming MDP+ Logic + Programming 19

DT-GOLOG: Decision Theoretic GOLOG S 2 S 0 S 1 GOLOG S 3 SNo Optimization 4 MDP Scaling is challenging All non-deterministic actions are optimized using MDP concepts. Uncertainty, Reward [Boutilier, et. al 00] 20

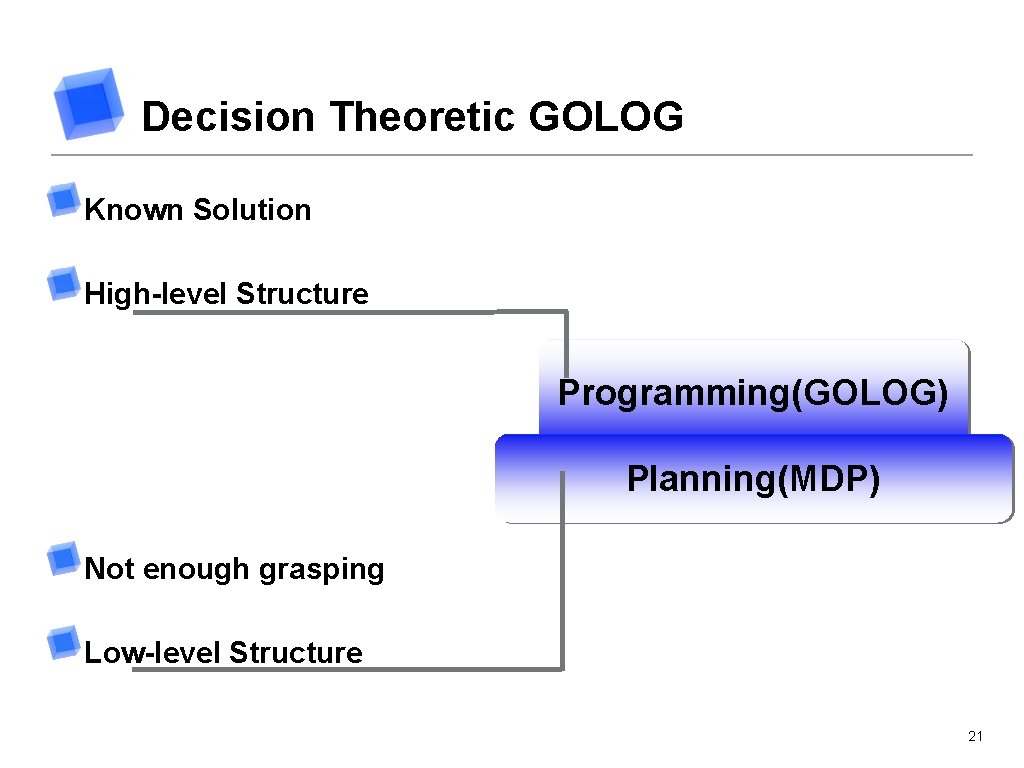
Decision Theoretic GOLOG Known Solution High-level Structure Programming(GOLOG) Planning(MDP) Not enough grasping Low-level Structure 21

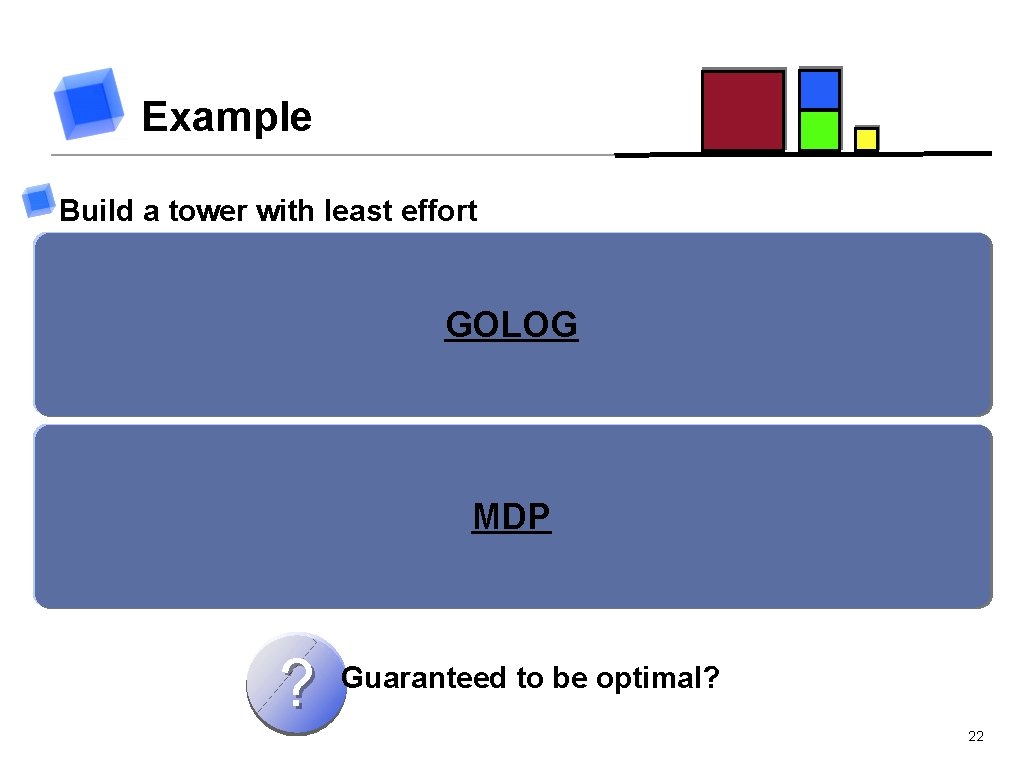
Example Build a tower with least effort Pick a block as base GOLOG Stack all other blocks on top of it Use which block for base? MDP In which order pick up the blocks ? Guaranteed to be optimal? 22

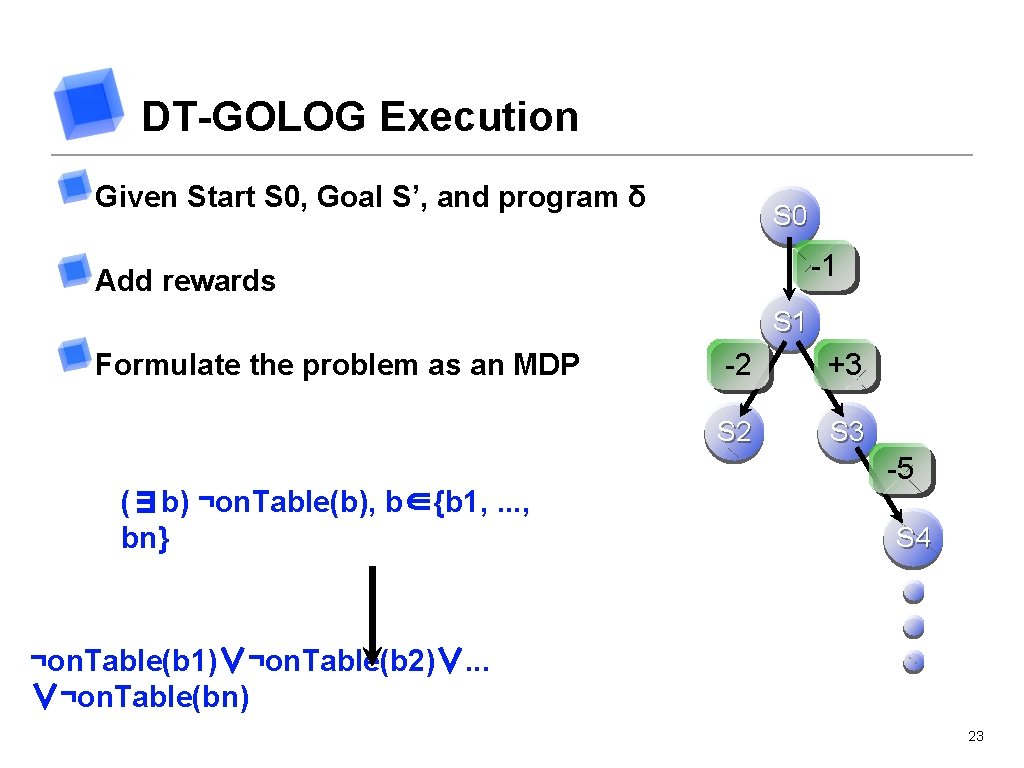
DT-GOLOG Execution Given Start S 0, Goal S’, and program δ S 0 -1 Add rewards S 1 Formulate the problem as an MDP (∃b) ¬on. Table(b), b∈{b 1, . . . , bn} -2 +3 S 2 S 3 -5 S 4 ¬on. Table(b 1)∨¬on. Table(b 2)∨. . . ∨¬on. Table(bn) 23

First Order Dynamic Programming [Sanner 07] Resulting MDP can still be intractable. Idea: Logical Structure Abstract Value Function Avoid curse of dimensionality! 24

Symbolic Dynamic Programming (Deterministic) Tabular: Symbolic ? Representation of Reward and Values Adding rewards and values Max Operator Find S 25

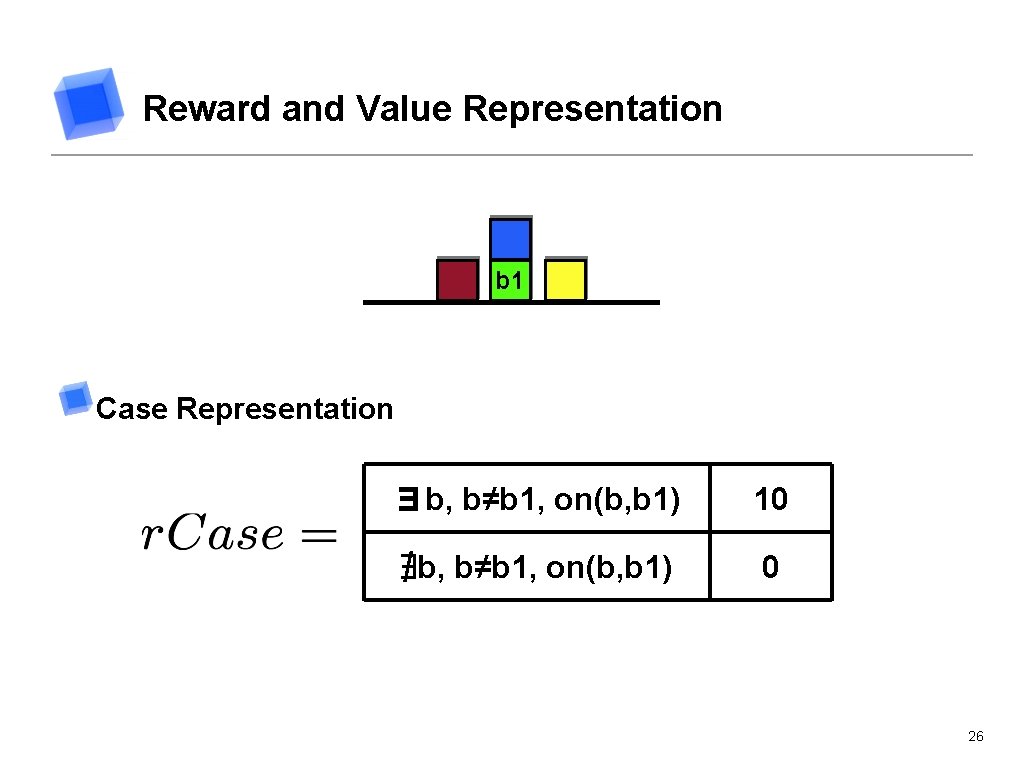
Reward and Value Representation b 1 Case Representation ∃b, b≠b 1, on(b, b 1) 10 ∄b, b≠b 1, on(b, b 1) 0 26

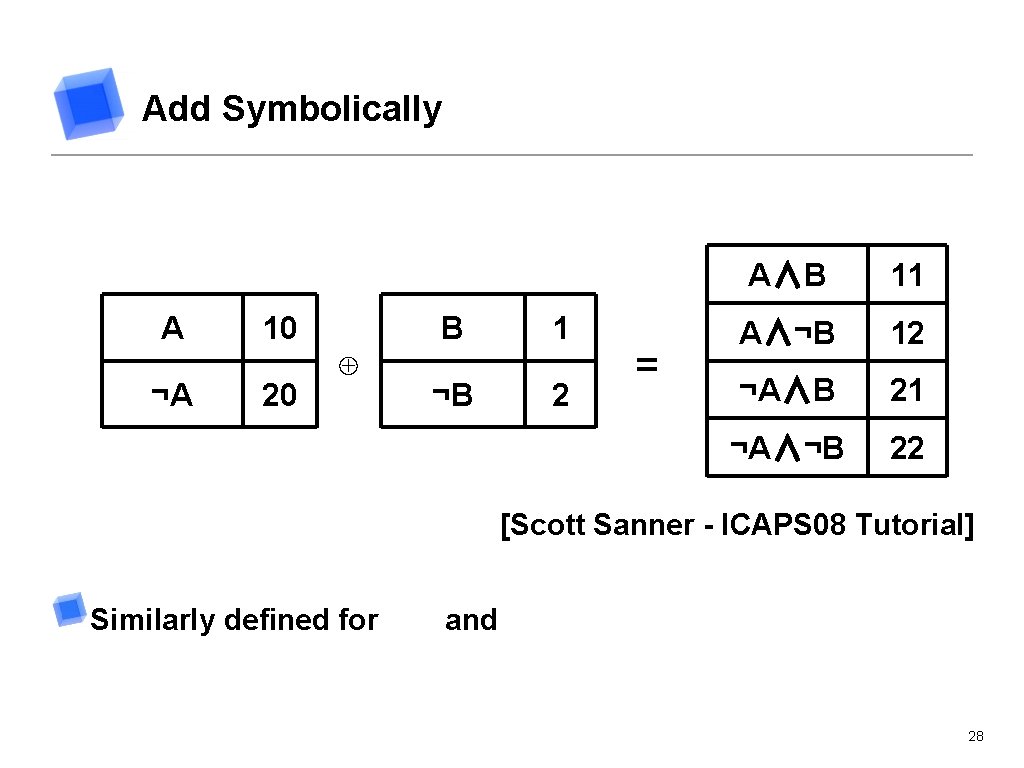
Add Symbolically A 10 ¬A 20 ⊕ B 1 ¬B 2 = A∧B 11 A∧¬B 12 ¬A∧B 21 ¬A∧¬B 22 [Scott Sanner - ICAPS 08 Tutorial] Similarly defined for and 28

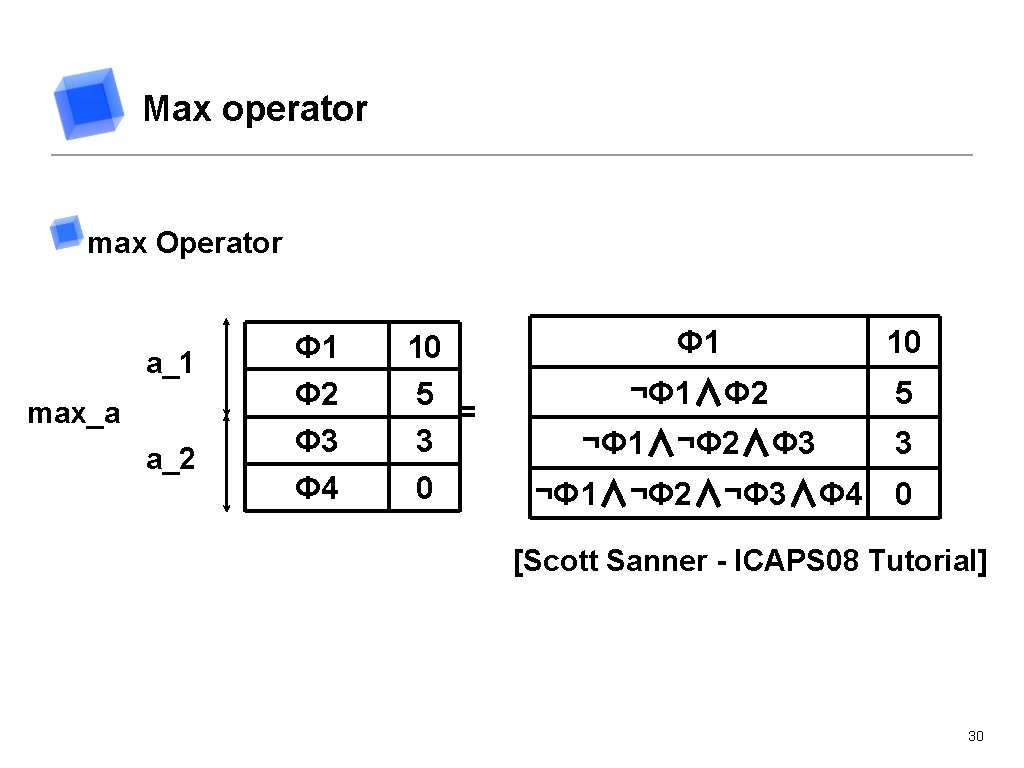
Max operator max Operator a_1 max_a a_2 Φ 1 Φ 2 Φ 3 Φ 4 10 5 = 3 0 Φ 1 10 ¬Φ 1∧Φ 2 5 ¬Φ 1∧¬Φ 2∧Φ 3 3 ¬Φ 1∧¬Φ 2∧¬Φ 3∧Φ 4 0 [Scott Sanner - ICAPS 08 Tutorial] 30

Find s? Isn’t it obvious? s a s’ Dynamic Programming: Given V(s’) find V(s) In MDPs, we have s explicitly. In symbolic representation we have it implicitly so we have to build it. 31

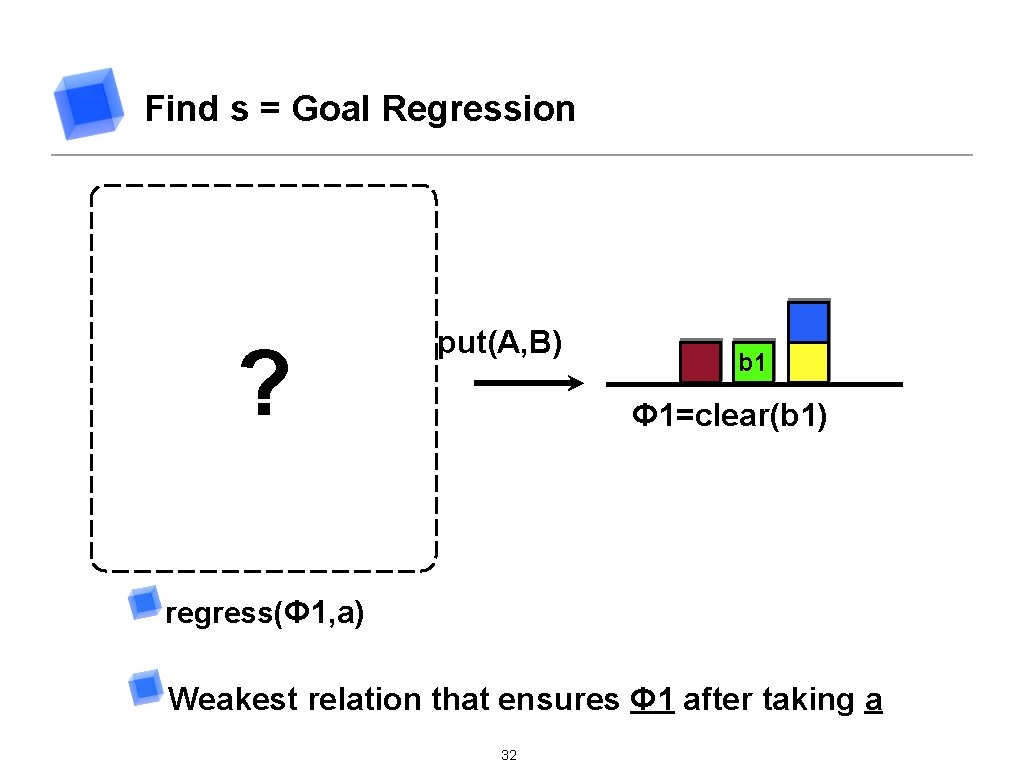
Find s = Goal Regression B b 1 Clear(b 1) ∧ B≠b 1 ? ∨ put(A, B) b 1 Φ 1=clear(b 1) A b 1 On(A, b 1) regress(Φ 1, a) Weakest relation that ensures Φ 1 after taking a 32

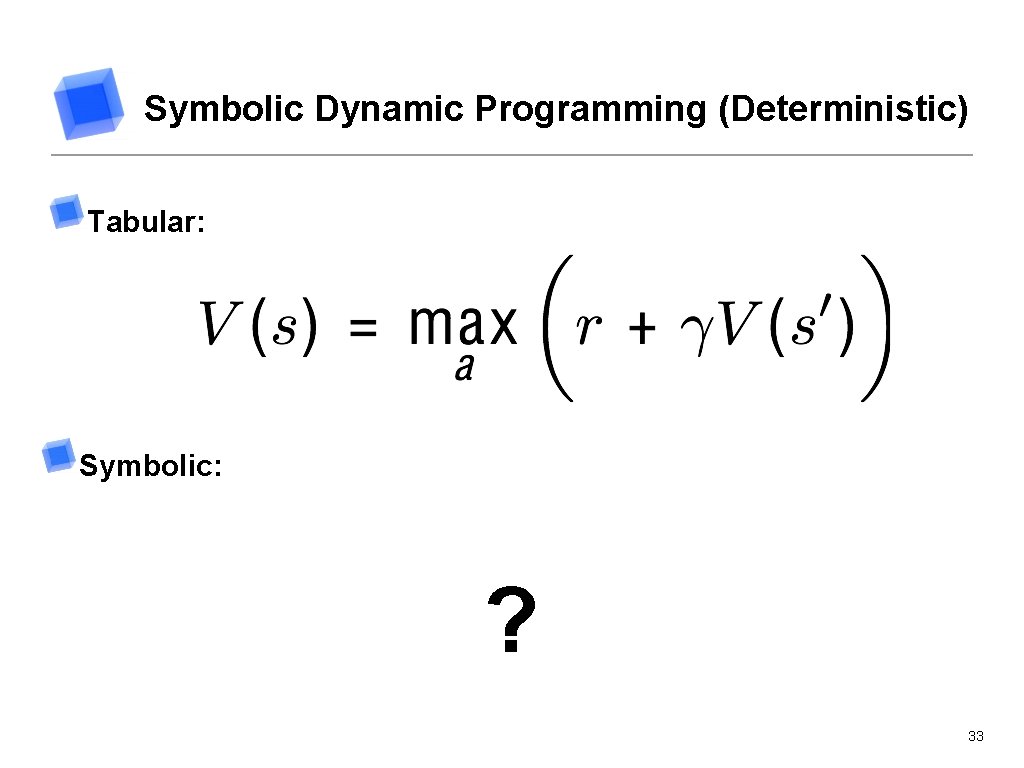
Symbolic Dynamic Programming (Deterministic) Tabular: Symbolic: ? 33

Classical Example Box Truck City Goal: Have a box in Paris ∃b, Box. In(b, Paris) 10 else 0 34

Classical Example Actions: drive(t, c 1, c 2), load(b, t), unload(b, t), noop load and unload have 10% chance of failure Fluents: Box. In(b, c), Box. On(b, t), Truck. In(t, c) Assumptions: All cities are connected. ϒ =. 9 35

Example [Sanner 07] s ∃b, Box. In(b, Paris) else, ∃b, t Truck. In(t, Paris) ∧ Box. On(b, t) else, ∃b, c, t Box. On(b, t) ∧ Truck. In(t, c) V*(s) π*(s) 100. noop 00 89. unload(b, t) 00 80. drive(t, c, paris) 00 72 load(b, t) else, ∃b, c, t Box. In(b, c) ∧ Truck. In(t, c) else, ∃b, c 1, c 2, t Box. In(b, c 1) ∧ 64. 7 drive(t, c 2, c 1) Truck. In(t, c 2) What did we gain by going through this? else 0 all ofnoop ? 36

Conclusion Logic Programming MDP Planning Review Situation Calculus Value Iteration GOLOG MDP+ Logic + Programming DT-GOLOG Symbolic DP 37

References Levesque, H. , Reiter, R. , Lespérance, Y. , Lin, F. , and Scherl, R. “ GOLOG: A Logic Programming Language for Dynamic Domains “, Journal of Logic Programming, 31: 59 --84, 1997 Richard S. Sutton, Andrew G. Barto, “Reinforcement Learning: An Introduction”, MIT Press, Cambridge, 1998 Craig Boutilier, Raymond Reiter, Mikhail Soutchanski, Sebastian Thrun, “Decision-Theoretic, High-Level Agent Programming in the Situation Calculus”. AAAI/IAAI 2000: 355 -362 S. Sanner, and K. Kersting, ”Symbolic dynamic programming”. Chapter to appear in C. Sammut, editor, Encyclopedia of Machine Learning, Springer-Verlag, 2007 38

References Craig Boutilier, Ray Reiter and Bob Price, “Symbolic Dynamic Programming for First-order MDPs”, Proceedings of the Seventeenth International Joint Conference on Artificial Intelligence (IJCAI), Seattle, pp. 690 --697 (2001). 39

Questions ? 40