Lecture 9 Rank Aggregation in Meta Search Meta



















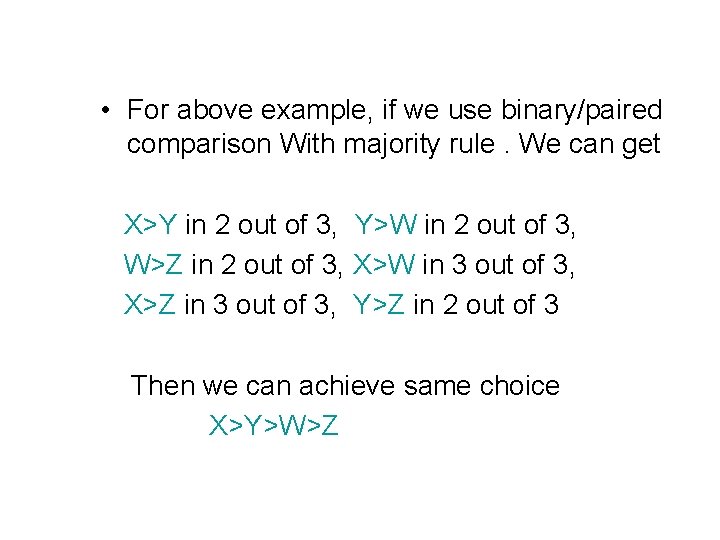










![Previous algorithms • Min, Max and Average Models [Fox and Shaw, 1995] • Linear Previous algorithms • Min, Max and Average Models [Fox and Shaw, 1995] • Linear](https://slidetodoc.com/presentation_image/88867fd13104cebc3a3bd4b2e5adf831/image-31.jpg)

















- Slides: 48

Lecture 9: Rank Aggregation in Meta. Search • Meta. Search Engine • Social Choice Rules • Rank Aggregation

Choices of Search Engines • Many search engines exist to compete for users – The results are not necessarily the same – Different users prefer different search engines – Search results may, in the future, be biased towards paid advertisements.

Meta. Search Engine • Metasearch Engines are designed to increase the coverage of web by forwarding users’ queries to multiple search engines – Users’ requests are sent to multiple search engines such as Allthe. Web, Google, MSN. • Then the results from the individual search engine are combined into a single result set to present to users.

Different Forms of Meta. Search • Submit different representations of the same query to the same search engine, then combine the results. • Submit the same query to several search engine adopting different information retrieval models, then combine the results.

Issues • How to combine the results retrieved by different source search engines is crucial for the success of a metasearch engine. • And this is the problem that social choice theory has been trying to answer.

Search Engine Watch • Interesting meta search engines are listed at – http: //www. searchenginewatch. com/links/article. ph p/2156241

Social Choice Theory • Studies on protocols that help a group of people make collective decisions, such as vote.

A Fundamental problem • Given a collection of agents (voters) – with preferences over different alternatives (allocations, outcomes), • how should society evaluate these alternatives and make a decision for all – that may be for the will of some voters but against that of others.

Applications • Voters elect president from several candidates. • National polls for economic or political policy of the government • The procedure or rule of election • The rank of metasearch engine obtained from those of search engines

Group Descisions How do we make decisions • Flip a coin? • Dictatorship? • Democracy (Majority rule)?

Group Decision Rules • Majority rule , • Condorcet paradox (voting cycle) • Borda rule

Mathematical model • A set of voters V={v 1, v 2, v 3, …, Vn} • A set of alternatives or outcomes S={s 1, s 2, s 3, …Sm}, with |S|=m; and • A set of preference relation P={R 1, R 2, R 3…Rn}, called a preference profile, – the preference relation Ri for each voter i is a permutation (order) of elements in S.

Example 1 Majority Rule • 3 rational people have rational preferences over 2 alternatives {x, y} Person 1 st 1 2 3 X Y X Pref. 1 : X>Y i. e. Person 2 : Y>X 2 nd Y X Y 3 : X>Y How to Aggregate their preferences? How to choose?

• Using majority rule. • Since more than ½ people (two out of three) prefer x to y. • Then the group prefers x to y

Example 2 Condorcet Paradox • 3 rational people have rational preferences over 3 alternatives {x, y, z} Person 1 st Pref. 2 nd 3 rd 1 2 X Y Y Z 3 Z X Z 1 : X>Y>Z X i. e. Person 2 : Y>Z>X Y 3 : Z>X>Y

Binary/paired Comparison With Majority rule • Person 1 2 3 1 st X Y Z 1 : X>Y Pref. 2 nd Y Z X for (x, y) 2 : Y>X X>Y 3 rd Z X Y 3 : X>Y • Similarly, for (Y, Z) we can get Y>Z; for (Z, X) we can get Z>X. • Then X>Y>Z>X (cycling) , Intransitive Not rational

• It was noted by Condorcet in the 18 century that no alternative can win a majority against all other alternatives. • Pairwise majority is not satisfactory in all cases.

Example 3 Borda Rule • For each voter, – associate the number 1 with the most preferred alternative, – 2 with the second and so on, • Assign to each alternative the number equal to – the sum of the numbers the individual voters assigned to the alternative.

Person 1 st 1 2 X(1) Y(1) Pref. 2 nd Y(2) 3 rd Z(3) 4 th W(4) 3 X(1) X(4) X X(2) W(2) Y(7) Y W(3) Z(10) W Z(4) Y(4) W(9) Z Then We get choice X>Y>W>Z
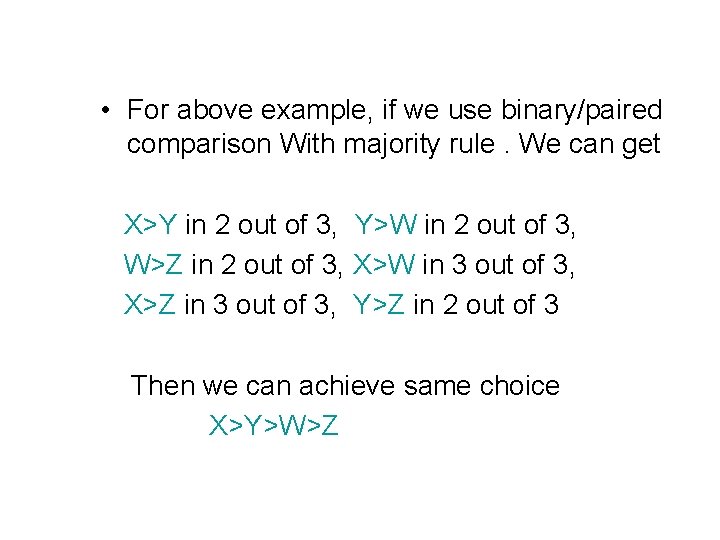
• For above example, if we use binary/paired comparison With majority rule. We can get X>Y in 2 out of 3, Y>W in 2 out of 3, W>Z in 2 out of 3, X>W in 3 out of 3, X>Z in 3 out of 3, Y>Z in 2 out of 3 Then we can achieve same choice X>Y>W>Z

• For the previous example we had trouble with majority rule via binary/paired comparison, we get a tie between all three alternatives with the Borda’s rule: – All three alternatives get a sum of 6.

• Some variations 1 with relevant scores available allotting each input system a point p to be distributed according to relevance scores of the documents. 2 Weighted Borda-rule Each voter may not have equal effectiveness to the final result. We may set more weight to good quality input systems.

• Condorcet winner algorithm It also comes from social choice theory. The Condorcet algorithm says that any candidate that can beat all other candidates in a head-to -head contest (pair-wise comparison) should win the election.

• Step 1, Construct Condorcet Graph. For each candidate pair (x, y), there exists an edge from x to y if x would receive at least as many votes as y in a head-to-head contest. In Condorcet graph, there is at least one directed edge between every pair of candidates. ( we call the graph is semi-complete) It may contains cycles in the graph. This is due to voting paradox of the condorcet voting.

• Step 2, We form a new acyclic graph from an old cyclic one by contracting all of the nodes in a cycle into one. It is a strongly connected component graph (SCCG). A directed graph is strongly connected if for any two nodes ua nd v, there are paths from u to v and from v to u. Definition of Strongly connected component(SCC): A strongly connected subgraph, S, of a directed graph, D, such that no vertex or subset of vertices of D can be added to S such that the new subgraph is still strongly connected.

The graph is totally orderable at the level of the SCC’s and each SCC is a “pocket” of cycles, within which each candidate is tied. (Why? ) Step 3, The condorcet-consistent Hamiltonian path is any Hamiltonian path through Condorcet graph. Definition Hamiltonian path: A path between two vertices of a graph that visits each vertex exactly once.

• Theorem 1. Suppose x and y are nodes in a graph g, and that X and Y are nodes of the associated SCCG G such that x X and y Y. If there exists a path from X to Y in G, then every Condorcet path of g has x before y. Refer to [Javed A. Aslam, Mark Montague 2001] for proof.

Rank Aggregation in Meta. Search Here we discussed two cases which using algorithm rooted at social choice theory for Meta. Search rank aggregation. • Data fusion track in TREC [Javed A. Aslam, Mark Montague 2001] Models for Metasearch in SIGIR 2001 • Rank aggregation for web search engine [Cynthia Dwork, Ravi Kumar, Moni Naor, D. Sivakumar 2001] Rank Aggregation Methods for the Web in WWW 10

Data fusion track in TREC • TREC (Text Retrieval Conference , see http: //trec. nist. gov/) maintains about 6 Gb of SGML tagged text, queries and respective answers for evaluation purposes. • The TREC organizers distribute data sets in advance and 50 new queries each year. • The competing teams then submit ranked lists of documents that their system gave in response to each query. And these retrieval systems will be evaluated.

• These ranked lists are available for metasearch researchers to download and use. • For each query, every retrieval system will return top 1000 documents and relevant score is available. • Then given these results retrieved by many different retrieval systems, how to aggregate them for better performance?
![Previous algorithms Min Max and Average Models Fox and Shaw 1995 Linear Previous algorithms • Min, Max and Average Models [Fox and Shaw, 1995] • Linear](https://slidetodoc.com/presentation_image/88867fd13104cebc3a3bd4b2e5adf831/image-31.jpg)
Previous algorithms • Min, Max and Average Models [Fox and Shaw, 1995] • Linear Combination Model [Bartell 1995] • Logistic Regression Model

Example • Min, Max and Average model The final score of each document d is based on the scores given to d by each input systems (voters). Algorithm Final score Comb. Min minimum of individual relevance scores Comb. Med median of individual relevance scores Comb. Max maximum of individual relevance scores Comb. Sum sum of individual relevance scores Comb. ANZ Comb. Sum / num non-zero relevance scores Comb. MNZ Comb. Sum * num non-zero relevance scores

• Linear Combination Model (LC model) The final score of document d is a simply linearly (each weighted differently) combining the normalized relevance scores given to each document. ai—weight si(d)—relevance score

Experiment result on TREC Model • The performance of rank aggregation is evaluated by average precision over the queries • Score-based borda-fuse (LC model) is usually the best method among several borda variant algorithms. • It is better than best input system over most of data collection. Such as TREC 3, TREC 5

Experiment result II • The performance of rank aggregation is evaluated by average precision over the queries. • Condorcet-fusion is the only algorithm that , without training data, ever matches the performance of the best input system over TREC 9. • Condorcet-fusion seems particularly sensitive to the dependence of input systems. If the input systems (voters) are too similar, the performance will decrease.

Rank aggregation methods for web New Challenges: Different from the case in TREC data fusion, – The coverage of various search engine is different – Thus some highly relevant web pages may not be ranked by some search engines. – Therefore, each voter ranks a partial candidate list

Preliminaries • Given a universe U, an ordered list with respect to U is an ordering of a subset S U, i. e. , , with each and is some ordering relation on S. • If contains – all the elements in U, then it is said to be a full list, – otherwise it is called partial list.

• Distance measures between two full lists with respect to a set S – The Kendall tau distance – It counts the number of pairwise disagreements between two lists. – The distance is given by – Normalize it by dividing the maximum possible value

• Spearman footrule distance • Given two full lists • Normalize it by dividing the maximum value and , the distance is given by

• Distance measures for more than 2 list Given several full lists , for instance, the normalized Footrule distance of to is given by If are partial lists, let U denote the union of elements in and let be a full list with respect to U. Considering the distance between and the projection of with respect to , we have the induced footrule distance

Optimal rank aggregation The question is Given (full or partial) lists , find a such that full list with respect to the union of the elements of minimizes is a The aggregation obtained by optimizing Kendall distance is called Kemeny optimal aggregation.

• When k>=4, computing the Kemeny optimal aggregation is NP-hard. (please refer to [Cynthia Dwork, Ravi Kumar, Moni Naor, D. Sivakumar 2001] for detailed proof ) We can use Spearman footrule distance to approximate the Kendall distance.

LCS approach (My own method) • Given n lists l 1, 1, l 1, 2, …, l 1, n 1; l 2, 1 , l 2, 2, …, l 2, n 2; l 3, 1, l 3, 2, …, l 3, n 3; …. . l m, 1, l m, 2, …, l m, nm, Find a longest common subsequence for these lists.

LCS approach (My own method) • LCS is NP-hard for m sequences if some elements appear twice in a sequence. • For the lists obtained by search engines, each document appears at most once. • There exists efficient algorithm to solve the problem for the special case. • Assume ni=nj for i, j=1, 2, ….

Efficient algorithm for LCS of m sequences • Fixed the order of the first sequence as 1, 2, …, n 1. • Define d(i) to be the length of LCS for the elements 1, 2, …, i that contains i in the LCS.

Computation of d(i, 1) and d(i, 2) d(i)=max k d(k)+1 such that k is always before i in all the m lists. (if k does not exist, d(i)=1. ) The length of the LCS is max d(i) for i=1, 2, …, n 1. A backtracking process can give the LCS.

An Example: l 1=1, 2, 3, 4, 5, 6, 7, 8, 9, 10. l 2=2, 1, 3, 4, 5, 6, 7, 9, 8, 10 l 3=2, 3, 5, 4, 1, 6, 7, 8, 9, 10 l 4=2, 3, 5, 7, 4, 6, 1, 7, 8, 9, 10 d(1)=1, d(2)=1. d(3)=d(2)+1=2. d(4)=d(3)+1=3. d(5)=d(3)+1=3. d(6)=d(5)+1=4. d(7)=d(6)+1=5. d(8)=d(7)+1=6. d(9)=d(7)+1=6. d(10)=d(9)+1=7. The final length is 7. the LCS is 2, 3, 4 , 6, 7, 8, 10 2, 3, 4, 6, 7, 9, 10 is a LCS, too.

When ni’s are different We delete those elements that are absent in some sequence. Examlple, l 1= 1, 2, 3, 4, 5, 6 l 2=2, 1, 5, 4, 6 l 3=2, 3, 4, 5, 6, l 4=1, 4, 3, 5, 6, since 1 is not in l 3, 2 is not in l 4 and 3 is not in l 2, we can compute the LCS for l’ 1= 4, 5, 6 l 2= 5, 4, 6 l 3= 4, 5, 6, l 4= 4, 5, 6. The final result is 4, 6.