Lecture 2 Greedy Algorithms II ShangHua Teng Optimization

Lecture 2: Greedy Algorithms II Shang-Hua Teng

Optimization Problems • A problem that may have many feasible solutions. • Each solution has a value • In maximization problem, we wish to find a solution to maximize the value • In the minimization problem, we wish to find a solution to minimize the value

Data Compression • Suppose we have 100000 (1 G) character data file that we wish to include in an email. • Suppose file only contains 26 letters {a, …, z}. • Suppose each letter a in {a, …, z} occurs with frequency fa. • Suppose we encode each letter by a binary code • If we use a fixed length code, we need 5 bits for each character • The resulting message length is 5( fa+ fb + … + fz) • Can we do better?

Huffman Codes • Most character code systems (ASCII, unicode) use fixed length encoding • If frequency data is available and there is a wide variety of frequencies, variable length encoding can save 20% to 90% space • Which characters should we assign shorter codes; which characters will have longer codes?

Data Compression: A Smaller Example • Suppose the file only has 6 letters {a, b, c, d, e, f} with frequencies Fixed length Variable length • Fixed length 3 G=300000 bits • Variable length

How to decode? • At first it is not obvious how decoding will happen, but this is possible if we use prefix codes

Prefix Codes • No encoding of a character can be the prefix of the longer encoding of another character, for example, we could not encode t as 01 and x as 01101 since 01 is a prefix of 01101 • By using a binary tree representation we will generate prefix codes provided all letters are leaves

Prefix codes • A message can be decoded uniquely. • Following the tree until it reaches to a leaf, and then repeat! • Draw a few more tree and produce the codes!!!

Some Properties • Prefix codes allow easy decoding – Given a: 0, b: 101, c: 100, d: 111, e: 1101, f: 1100 – Decode 001011101 going left to right, 0|01011101, a|0|1011101, a|a|101|1101, a|a|b|e • An optimal code must be a full binary tree (a tree where every internal node has two children) • For C leaves there are C-1 internal nodes • The number of bits to encode a file is where f(c) is the freq of c, d. T(c) is the tree depth of c, which corresponds to the code length of c

Optimal Prefix Coding Problem • Input: Given a set of n letters (c 1, …, cn) with frequencies (f 1, …, fn). • Construct a full binary tree T to define a prefix code that minimizes the average code length

Greedy Algorithms • Many optimization problems can be solved more quickly using a greedy approach – The basic principle is that local optimal decisions may be used to build an optimal solution – But the greedy approach may not always lead to an optimal solution overall for all problems – The key is knowing which problems will work with this approach and which will not • We will study – The problem of generating Huffman codes

Greedy algorithms • A greedy algorithm always makes the choice that looks best at the moment – My everyday examples: • • Driving in Los Angeles, or even Boston for that matter Playing cards Invest on stocks Choose a university – The hope: a locally optimal choice will lead to a globally optimal solution – For some problems, it works • greedy algorithms tend to be easier to code

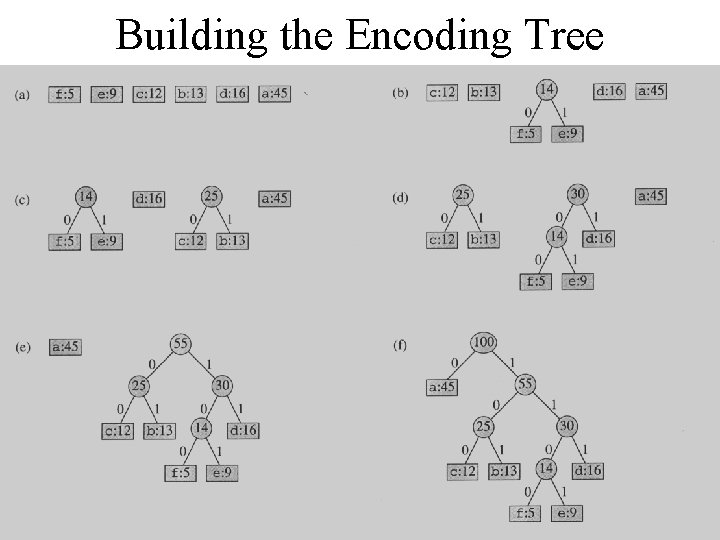
David Huffman’s idea • A Term paper at MIT • Build the tree (code) bottom-up in a greedy fashion • Origami aficionado

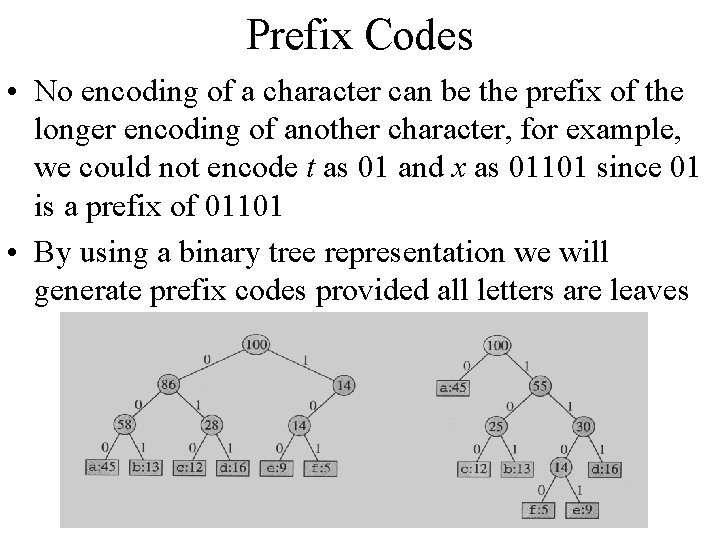
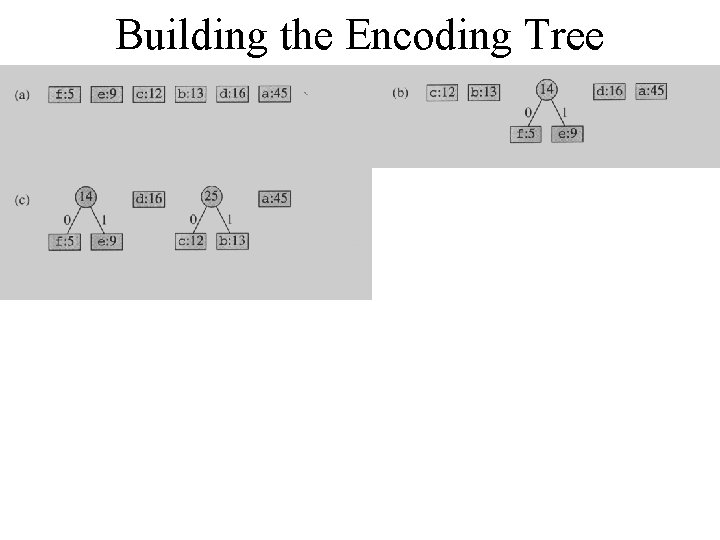
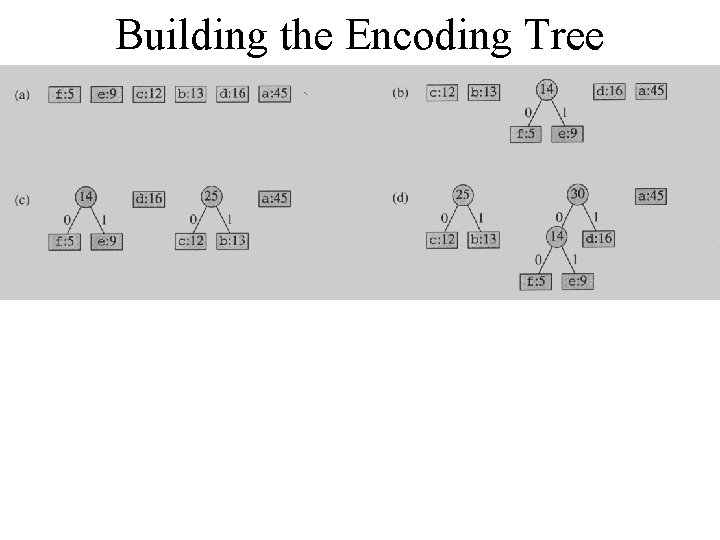
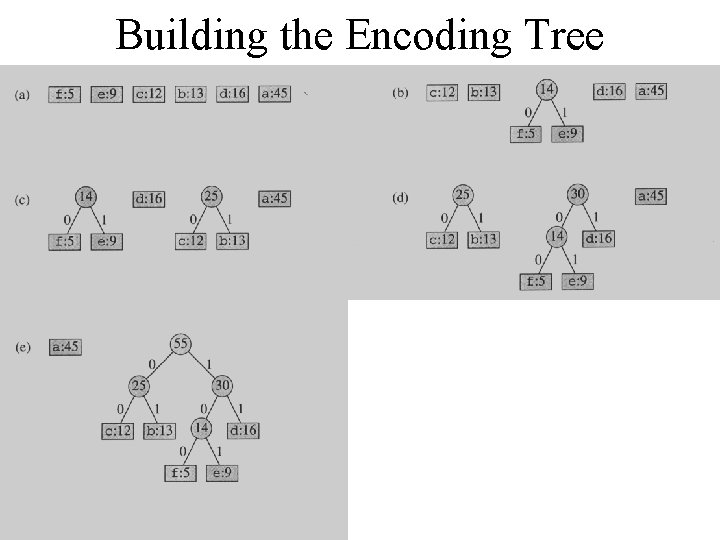
Building the Encoding Tree

Building the Encoding Tree

Building the Encoding Tree

Building the Encoding Tree

Building the Encoding Tree

The Algorithm • An appropriate data structure is a binary min-heap • Rebuilding the heap is lg n and n-1 extractions are made, so the complexity is O( n lg n ) • The encoding is NOT unique, other encoding may work just as well, but none will work better

Correctness of Huffman’s Algorithm Lemma A: Since each swap does not increase the cost, the resulting tree T’’ is also an optimal tree

Proof of Lemma A • Without loss of generality, assume f[a] f[b] and f[x] f[y] • The cost difference between T and T’ is B(T’’) B(T), but T is optimal, B(T) B(T’’) = B(T) Therefore T’’ is an optimal tree in which x and y appear as sibling leaves of maximum depth

Correctness of Huffman’s Algorithm Lemma B: • Observation: B(T) = B(T’) + f[x] + f[y] B(T’) = B(T)-f[x]-f[y] –For each c C – {x, y} d. T(c) = d. T’(c) f[c]d. T(c) = f[c]d. T’(c) –d. T(x) = d. T(y) = d. T’(z) + 1 –f[x]d. T(x) + f[y]d. T(y) = (f[x] + f[y])(d. T’(z) + 1) = f[z]d. T’(z) + (f[x] + f[y])

B(T’) = B(T)-f[x]-f[y] z: 14 B(T’) = 45*1+12*3+13*3+(5+9)*3+16*3 = B(T) - 5 - 9 B(T) = 45*1+12*3+13*3+5*4+9*4+16*3

Proof of Lemma B • Prove by contradiction. • Suppose that T does not represent an optimal prefix code for C. Then there exists a tree T’’ such that B(T’’) < B(T). • Without loss of generality, by Lemma A, T’’ has x and y as siblings. Let T’’’ be the tree T’’ with the common parent x and y replaced by a leaf with frequency f[z] = f[x] + f[y]. Then • B(T’’’) = B(T’’) - f[x] – f[y] < B(T) – f[x] – f[y] = B(T’) – T’’’ is better than T’ contradiction to the assumption that T’ is an optimal prefix code for C’

How Did I learn about Huffman code? • I was taking Information Theory Class at USC from Professor Irving Reed (Reed-Solomon code) • I was TAing for CSCI 303 • I taught a lecture on “Huffman Code“ for Professor Miller • I wrote a paper

Stable Matching (Marriage) Problem -- Continue Shang-Hua Teng

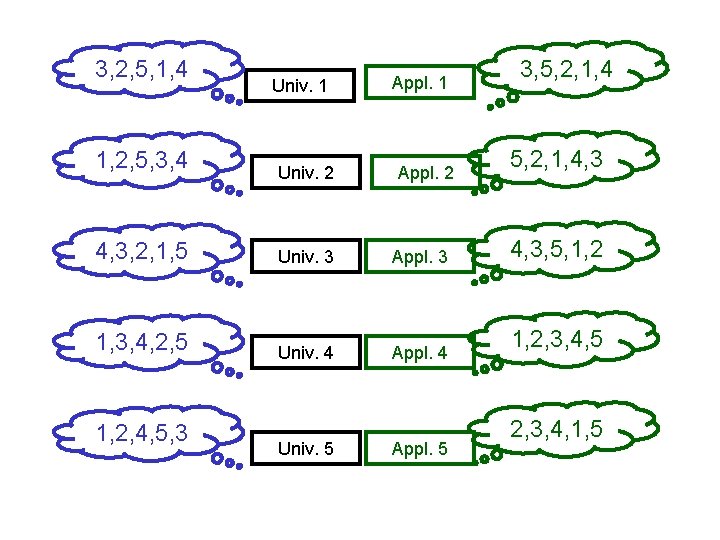
3, 2, 5, 1, 4 1, 2, 5, 3, 4 Univ. 1 Univ. 2 Appl. 1 Appl. 2 4, 3, 2, 1, 5 Univ. 3 Appl. 3 1, 3, 4, 2, 5 Univ. 4 Appl. 4 1, 2, 4, 5, 3 Univ. 5 Appl. 5 3, 5, 2, 1, 4, 3, 5, 1, 2, 3, 4, 5 2, 3, 4, 1, 5

Stability: “Mutually Cheating Hearts” • Suppose we pair off all the university and candidate. Now suppose that some university and some candidate prefer each other to what they matched to. • They will be called a pair of MCHs or blocking pair

Gale-Shapley Algorithm • For each day each university still has an opening does the following: – Morning • Make an offer to the best candidate to whom it has not yet offered to – Afternoon (for those candidates with at least one offer) • To today’s best suitor: “Maybe, but for now I will keep your offer” • To any others: “Not me, but good luck” – Evening • Each university is ready to offer to the next candidate on its list The day WILL COME that no university is rejected Each candidate accepts the last university to whom she/he said “maybe”

Improvement Lemma: If a candidate has an offer, then she/he will always have an offer from now on. Corollary: Each candidate will accept her/his absolute best offer received during the process. [Advantage to candidate? ] Corollary: No University can be rejected by all the candidates Corollary: A matching is achieved by Gale-Shapley

Theorem: The pairing produced by Gale. Shapley is stable. – Proof by contradiction: Suppose USC and Adleman are a pair of MCHs. – This means USC prefers Adleman more than the person it matched to, say, Lee. – Thus, USC offered to Adleman before it offered to Lee. – Adleman must have rejected USC for another university he preferred. – By the Improvement lemma, he must like his current university, saying, UCLA more than USC. Contradiction!

Each candidate will accept her/his absolute best offer received during the process. [Power to reject: Advantage to candidate? ] But university has the power to determine when and whom to make an offer to [Power to choose: Advantage to University]

Opinion Poll in f f o r e t t e pley b is a h o e h S h t W ale , e m h t h G t i r r o o Alg risties es? e idat v i un and c

• How should we define what we mean when we say “the optimal candidate for USC”? Flawed Attempt: “The candidate at the top of USC’s list”

The Optimal Match A university’s optimal match is the highest ranked candidate for whom there is some stable pairing in which they are matched The candidate is the best candidate it can conceivably be matched in a stable world. Presumably, that candidate might be better than the candidate it gets matched to in the stable pairing output by Gale-Shapley.

The Pessimal Match A university’s pessimal match is the lowest ranked candidate for whom there is some stable pairing in which the university is matched to. That candidate is the least ranked candidate the university can conceivably get to be matched to in a stable world.

Dilemmas: power to reject or power to choose • A pairing is university-optimal if every university gets its optimal candidate. This is the best of all possible stable worlds for every university simultaneously. • A pairing is university-pessimal if every university gets its pessimal candidate. This is the worst of all possible stable worlds for every university simultaneously.

Dilemmas: power to reject or power to choose • A pairing is candidate-optimal if every candidate gets her/his optimal job. This is the best of all possible stable worlds for every candidate simultaneously. • A pairing is candidate-pessimal if every candidate gets her/his pessimal job. This is the worst of all possible stable worlds for every candidate simultaneously.

The Mathematical Truth is! The Gale-Shapley Algorithm always produces a universityoptimal, and candidatepessimal pairing.

Theorem: Gale-Shapley produces a university-optimal pairing – Suppose not: i. e. that some univ. gets rejected by it optimal match during GS. – In particular, let’s say UCLA is the first univ to be rejected by its optimal match Adleman: Let’s say Adleman said “maybe” to USC, whom he prefers. – Since UCLA was the only univ. to be rejected by its optimal match so far, USC must like Adleman at least as much as USC’s optimal match.

We are assuming that Adleman is UCLA’s optimal match: Adleman likes USC more than UCLA. USC likes Adleman at least as much as its optimal match. • We now show that any pairing S in which UCLA hires Adleman cannot be stable (for a contradiction). • Suppose S is stable: – USC likes Adleman more than his partner in S • USC likes Adleman at least as much as USC’s best match, but USC is not matched to Adleman in S – Adleman likes USC more than his university UCLA in S Contradiction!

• We’ve shown that any pairing in which UCLA hires Adleman cannot be stable. – Thus, Adleman cannot be UCLA’s optimal match (since he can never work there in a stable world). – So UCLA never gets rejected by its optimal match in the Gale-Shapley, and thus the Gale. Shapley is university-optimal.

Theorem: The Gale-Shapley pairing is candidate -pessimal.