PERTEMUAN 12 METODE GREEDY METODE GREEDY Untuk mendapatkan





























- Slides: 30

PERTEMUAN 12 METODE GREEDY

METODE GREEDY Untuk mendapatkan solusi optimal dr permasalahan yg mempunyai dua kriteria yaitu Fungsi Tujuan/Utama & nilai pembatas (constrain)

METODE GREEDY (Lanjutan) Proses Kerja Metode Greedy : Untuk menyeselesaikan suatu permasalahan dgn n input data yg terdiri dari beberapa fungsi pembatas & 1 fungsi tujuan yg diselesaikan dgn memilih beberapa solusi yg mungkin (feasible solution/feasible sets), yaitu bila telah memenuhi fungsi tujuan/obyektif.

Contoh Persoalan Optimasi: (Masalah Penukaran Uang): Diberikan uang senilai A. Tukar A dengan koin-koin uang yang ada. Berapa jumlah minimum koin yang diperlukan untuk penukaran tersebut?

Persoalan Optimasi (Lanjutan) Contoh 1: tersedia banyak koin 1, 5, 10, 25 • Uang senilai A = 32 dapat ditukar dengan banyak cara berikut: 32 = 1 + … + 1 (32 koin) 32 = 5 + 5 + 10 + 1 (7 koin) 32 = 10 + 1 (5 koin) … dst • Minimum: 32 = 25 + 1 + 1 (4 koin)

METODE GREEDY (Lanjutan) • Greedy = rakus, tamak, loba, … • Prinsip greedy: “take what you can get now!”. • Algoritma greedy membentuk solusi langkah per langkah (step by step). • Pada setiap langkah, terdapat banyak pilihan yang perlu dieksplorasi. • Oleh karena itu, pada setiap langkah harus dibuat keputusan yang terbaik dalam menentukan pilihan.

METODE GREEDY (Lanjutan) Metode GREEDY digunakan dlm penyelesaian masalah - masalah : 1. Optimal On Tape Storage Problem 2. Knapsack Problem 3. Minimum Spanning Tree Problem 4. Shortest Path Problem.

1. Optimal On Tape Storage Problem Permasalahan Bagaimana mengoptimalisasi storage/memory dalam komputer agar data yg disimpan dapat termuat dgn optimal. Misalkan terdapat n program. yg akan disimpan didalam pita (tape). Pita tsb mempunyai panjang maks. sebesar L, masing 2 prg. yg akan disimpan mempunyai panjang L 1, L 2, L 3. . . , Ln. Cara penyimpanan adalah penyimpanan secara terurut (sequential).

Optimal On Tape Storage Problem (Lanjutan) L 1 L 2 L 3 . . . Ln Persoalan = Bagaimana susunan penyimpanan program 2 tersebut sehingga L 1 + L 2 + L 3 +. . . + Ln = L ? Pemecahannya = jika program. 2 tersebut disimpan dlm Order, dimisalkan adalah Order I, yaitu : j sama dengan tik maka akan didapat k=1

Optimal On Tape Storage Problem (Lanjutan) n Mean Retrieval Time (MRT) = tj /n j=1 n j dan Optimal Storage = D(I) = lik j=1 k=1

Contoh soal Optimal On Tape Storage Problem Misal terdapat 3 buah prg. (n=3) yg masing 2 mpy panjang prg. (I 1, I 2, I 3)=(5, 10, 3). Tentukan urutan penyimpanannya scr berurutan (sequential) agar optimal. . !

Penyelesaiannya Soal Optimal On Tape Storage Problem Dari 3 program tersebut akan didapat 6 buah kemungkinan order, yg didapat dr nilai faktorial 3 3! (ingat faktorial n!). ORDERING D(I) 1, 2, 3 5 + (5+10) + (5+10+3) = 38 1, 3, 2 5 + (5+3) + (5+3+10) = 31 2, 1, 3 10 + (10+5) + (10+5+3) = 43 2, 3, 1 10 + (10+3) + (10+3+5) = 41 3, 1, 2 3 + (3+5) + (3+5+10) = 29 3, 2, 1 3 + (3+10) + (3+10+5) = 34

Optimal On Tape Storage Problem (Lanjutan) Dari tabel tersebut, didapat Susunan/order yg optimal, sbb : susunan pertama untuk program ke tiga susunan kedua untuk program kesatu susunan ketiga untuk program kedua

2. KNAPSACK Problem Kasus : Terdapat n obyek (Xi; i=1, 2, 3, . . n) yang masing-masing mempunyai berat (weight)/ Wi & masing-masing memiliki nilai (profit)/Pi yg berbeda-beda.

Masalah KNAPSACK Problem Bagaimana obyek-obyek tersebut dimuat / dimasukan kedalam ransel (knapsack) yg mempunyai kapasitas maks. =M. Sehingga timbul permasalahan sbb: Bagaimana memilih obyek yg akan dimuat dr n obyek yg ada sehingga nilai obyek termuat jumlahnya sesuai dgn kapasitas( M) Jika semua obyek harus dimuat kedalam ransel maka berapa bagian dr setiap obyek yg ada dapat dimuat kedalam ransel sedemikian shg nilai kum. maks. & sesuai dgn kapasitas ransel ?

Penyelesaian Knapsack Problem 1. Dengan Secara Matematika 2. Dengan Kriteria Greedy. 3. Dengan Algoritma Pemrograman Greedy.

Penyelesaian Knapsack Dengan Secara Matematika Fungsi tujuan = fungsi utama/obyektif = fungsi yg mjd penyelesaian permasalahan dgn mendptkan solusi yg optimal. Solusi dimaksud = menemukan nilai/profit yg maks. utk jml obyek yg dimuat dlm ransel shg sesuai kapasitas. n Fungsi Tujuan Maksimum : Pi Xi I=1

Penyelesaian Knapsack Dengan Secara Matematika (Lanjutan) Fungsi pembatas = fungsi subyektif = fungsi yg bertujuan untuk memberikan batas maks. dr setiap obyek untuk dapat dimuat dalam ransel sehingga kapasitasnya tdk melebihi dr jumlah maks. daya tampung ransel. n Fungsi Pembatas : Wi Xi M i=1 dimana : 0 Xi 1; Pi >0; Wi>0 Catatan : karena dengan menggunakan Matematikan sangat sulit dan rumit maka tidak dibahas lebih mendalam.

Penyelesaian Dengan Kriteria Greedy Konsep dr kriteria yg ditawarkan oleh metode Greedy yaitu : Pilih obyek (barang) dengan nilai Pi maximal atau terbesar Pilih obyek (barang) dengan berat Wi minimal dahulu. Pilih obyek (barang) dgn perbandingan nilai & berat yaitu Pi/Wi yang terbesar.

Contoh Soal Kriteria Greedy Diketahui bahwa kapasitas M = 20 kg , Dengan jumlah barang n=3 Berat Wi masing-masing barang (W 1, W 2, W 3) = (18, 15, 10) Nilai Pi masing-masing barang (P 1, P 2, P 3) = (25, 24, 15)

Penyelesaian Soal Kriteria Greedy Pilih barang dengan Nilai Profit Maksimal P 1 = 25 X 1 = 1, dimisalkan sebagai atas nilai P 2 = 24 X 2 = 2/15, dihitung dengan Fungsi Pembatas P 3 = 15 X 3 = 0, dimisalkan sebagai batas bawah nilai

Penyelesaian Soal Kriteria Greedy (Lanjutan 1) Pilih barang dengan Berat Minimal W 1 = 18 X 1 = 0, sebagai batas bawah W 2 = 15 X 2 = 2/3, dihitung dgn Fungsi Pembatas W 3 = 10 X 3 = 1, sebagai batas

Penyelesaian Soal Kriteria Greedy (Lanjutan 2) Pilih barang dgn menghitung perbandingan yg terbesar dr Profit dibagi Berat (Pi/Wi) yg diurut secara tidak naik, yaitu : P 1/W 1 = 25/18 karena terkecil maka X 1 = 0 P 2/W 2 = 24/15 karena terbesar maka X 2 = 1 P 3/W 3 = 15/10 dengan Fungsi pembatas X 3 = 1/2.

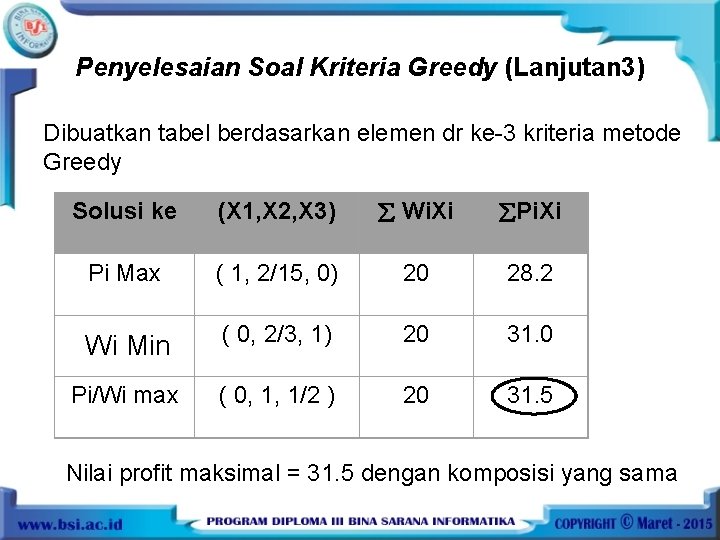
Penyelesaian Soal Kriteria Greedy (Lanjutan 3) Dibuatkan tabel berdasarkan elemen dr ke-3 kriteria metode Greedy Solusi ke (X 1, X 2, X 3) Wi. Xi Pi. Xi Pi Max ( 1, 2/15, 0) 20 28. 2 Wi Min ( 0, 2/3, 1) 20 31. 0 Pi/Wi max ( 0, 1, 1/2 ) 20 31. 5 Nilai profit maksimal = 31. 5 dengan komposisi yang sama

PERTEMUAN 12 LATIHAN SOAL

Latihan Soal 1. Metode Greedy dapat digunakan untuk menyelesaikan masalah dibawah ini , kecuali : a. Knapsack Problem d. Minimum Spanning tree b. Shortest Path Problem e. Searching c. Faktorial 2. Permasalahan bagaimana mengoptimalisasi storage/ memory dalam computer agar data yang disimpan dapat termuat dengan optimal, merupakan bentuk permasalahan dari : a. Knapsack problem b. Shortest Path Problem c. Minimum Spanning Tree d. Optimal On Tape Storage Problem e. Searching

Latihan Soal 2. Permasalahan bagaimana mengoptimalisasi storage/ memory dalam computer agar data yang disimpan dapat termuat dengan optimal, merupakan bentuk permasalahan dari : a. Knapsack problem b. Shortest Path Problem c. Minimum Spanning Tree d. Optimal On Tape Storage Problem e. Searching 3. Misal terdapat 3 buah program ( n= 5 ) yang masing-masing mempunyai panjang program ( I 1, I 2, I 3, I 4, I 5)= (15, 8, 10, 22, 9) Tentukan Urutan penyimpanannya : a. I 4, I 1, I 3, I 5, I 2 d. I 4, I 1, I 2, I 5, I 1 b. I 2, I 5, I 3, I 1, I 4 e. Salah Semua c. I 2, I 4, I 3, I 1, I 5

Latihan Soal 3. Misal terdapat 3 buah program ( n= 5 ) yang masing- masing mempunyai panjang program (I 1, I 2, I 3, I 4, I 5)= (15, 8, 10, 22, 9) Tentukan Urutan penyimpanannya: a. I 4, I 1, I 3, I 5, I 2 d. I 4, I 1, I 2, I 5, I 1 b. I 2, I 5, I 3, I 1, I 4 e. Salah Semua c. I 2, I 4, I 3, I 1, I 5 4. Penyelesaian knapsack dengan Kriteria Greedy adalah dengan konsep dibawah ini, kecuali : a. Pilih obyek dengan nilai Pi maximal b. Pilih obyek dengan berat Wi minimal c. Pilih obyek dengan Pi/Wi maximal d. Pilih obyek dengan berat Wi maximal e. Pilih obyek dengan Pi minimal

Latihan Soal 4. Penyelesaian knapsack dengan Kriteria Greedy adalah dengan konsep dibawah ini, kecuali : a. Pilih obyek dengan nilai Pi maximal b. Pilih obyek dengan berat Wi minimal c. Pilih obyek dengan Pi/Wi maximal d. Pilih obyek dengan berat Wi maximal e. Pilih obyek dengan Pi minimal 5. Dalam kasus menentukan obyek yang akan dimuat dalam suatu kantong, masing-masing Obyek dari n obyek tersebut harus mempunyai : a. Berat dan Profit d. Panjang dan Lebar b. Berat dan Panjang e. Profit dan berat c. Profit saja

Latihan Soal 5. Dalam kasus menentukan obyek yang akan dimuat dalam suatu kantong, masing-masing Obyek dari n obyek tersebut harus mempunyai : a. Berat dan Profit d. Panjang dan Lebar b. Berat dan Panjang e. Profit dan berat c. Profit saja 1. Metode Greedy dapat digunakan untuk menyelesaikan masalah dibawah ini , kecuali : a. Knapsack Problem d. Minimum Spanning tree b. Shortest Path Problem e. Searching c. Faktorial