KRUGOVI U SVAKIDANJEM IVOTU Krunica Skup svih toaka

KRUGOVI U SVAKIDAŠNJEM ŽIVOTU

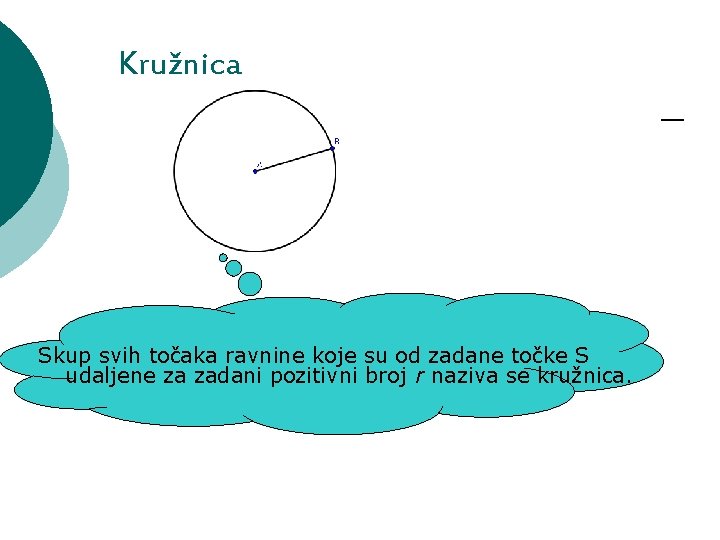
Kružnica Skup svih točaka ravnine koje su od zadane točke S udaljene za zadani pozitivni broj r naziva se kružnica.

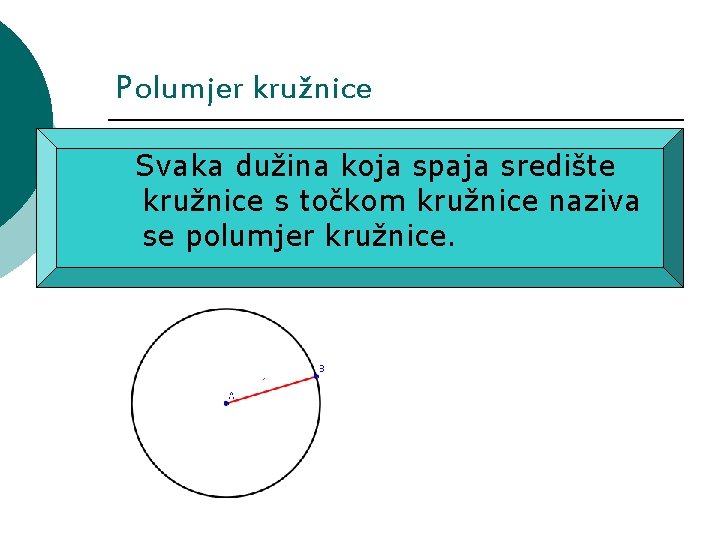
Polumjer kružnice Svaka dužina koja spaja središte kružnice s točkom kružnice naziva se polumjer kružnice.

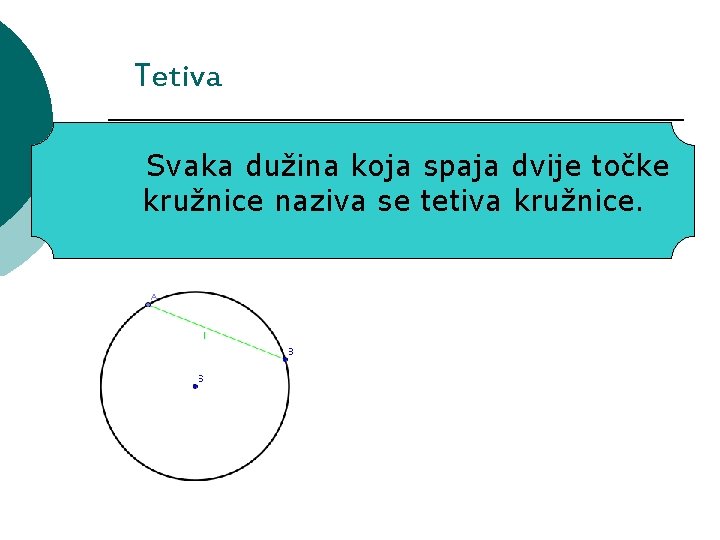
Tetiva Svaka dužina koja spaja dvije točke kružnice naziva se tetiva kružnice.

Promjer kružnice Svaka dužina koja sadrži središte kružnice i spaja dvije točke te kružnice naziva se promjer kružnice.

Kružni luk ¡ Dio kružnice omeđen dvjema njezinim točkama naziva se kružni luk.

Polukružnica Kružni luk omeđen krajnjim točkama promjera naziva se polukružnica.

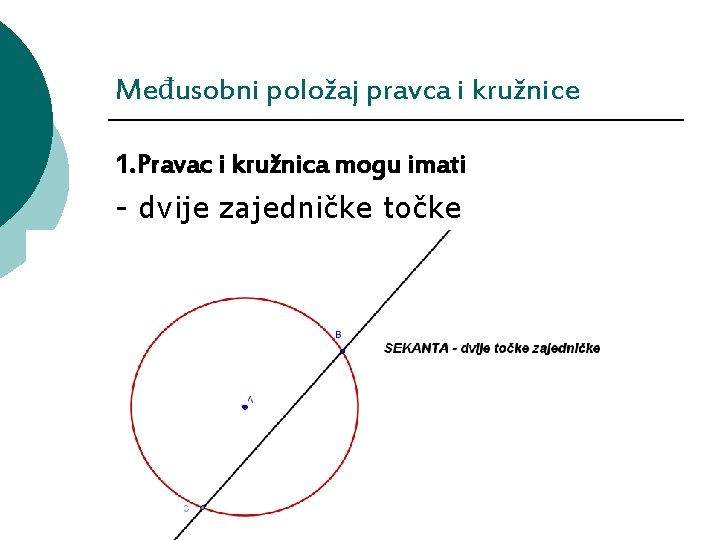
Međusobni položaj pravca i kružnice 1. Pravac i kružnica mogu imati - dvije zajedničke točke

2. Jednu zajedničku točku

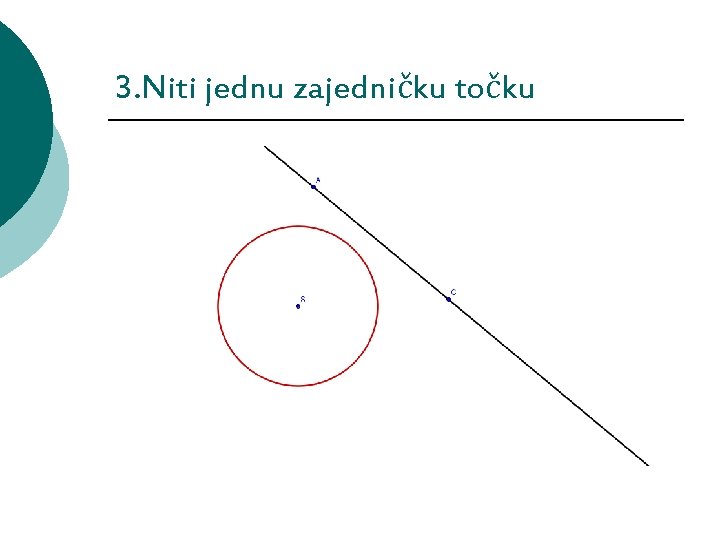
3. Niti jednu zajedničku točku

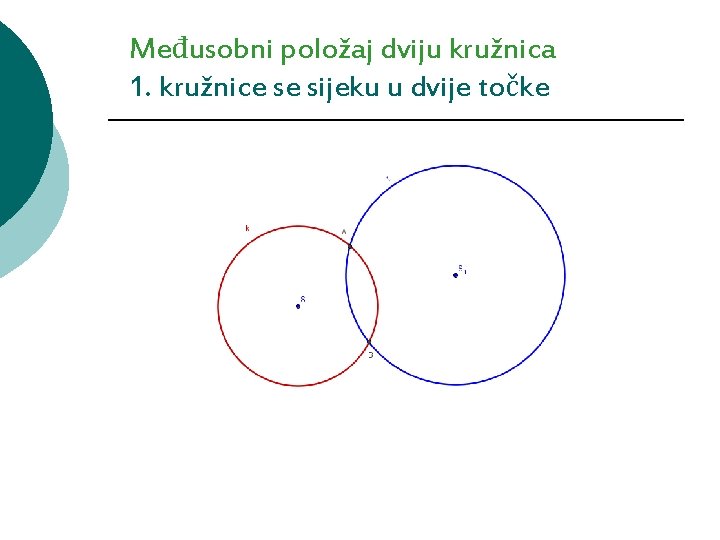
Međusobni položaj dviju kružnica 1. kružnice se sijeku u dvije točke

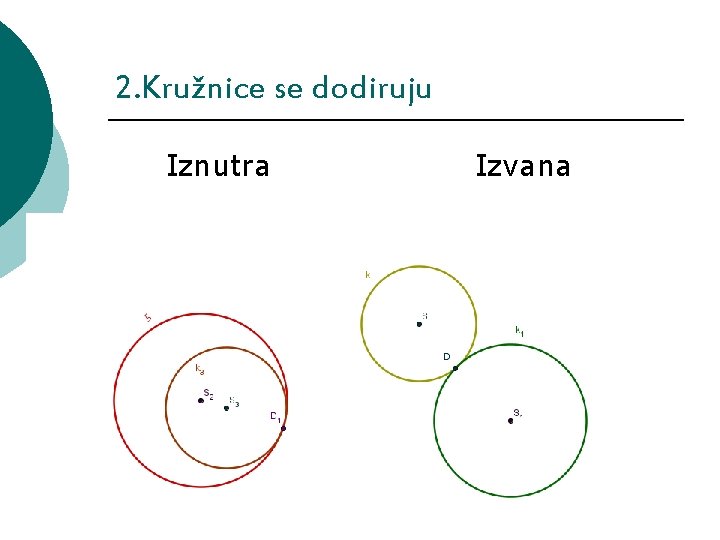
2. Kružnice se dodiruju Iznutra Izvana

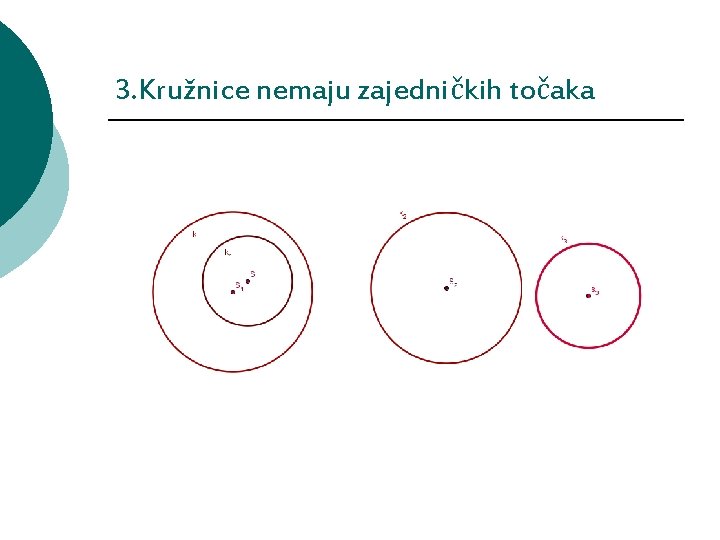
3. Kružnice nemaju zajedničkih točaka

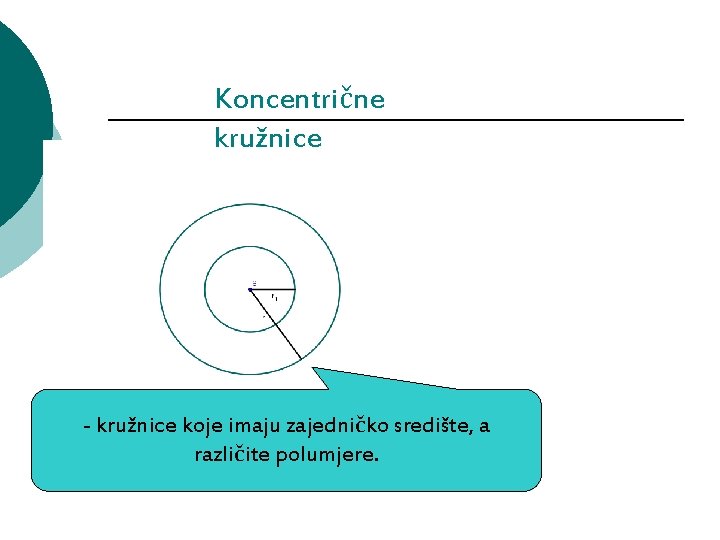
Koncentrične kružnice - kružnice koje imaju zajedničko središte, a različite polumjere.

Krug Dio ravnine omeđen kružnicom naziva se krug.

Dijelovi kruga 1. Kružni isječak Dio kruga omeđen kružnim lukom i pripadnim polumjerima.

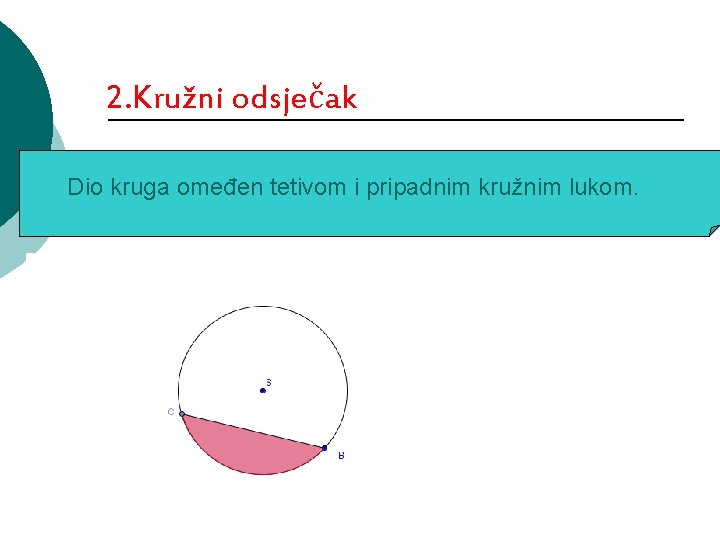
2. Kružni odsječak Dio kruga omeđen tetivom i pripadnim kružnim lukom.

3. Polukrug Dio kruga omeđen promjerom i polukružnicom naziva se polukrug.

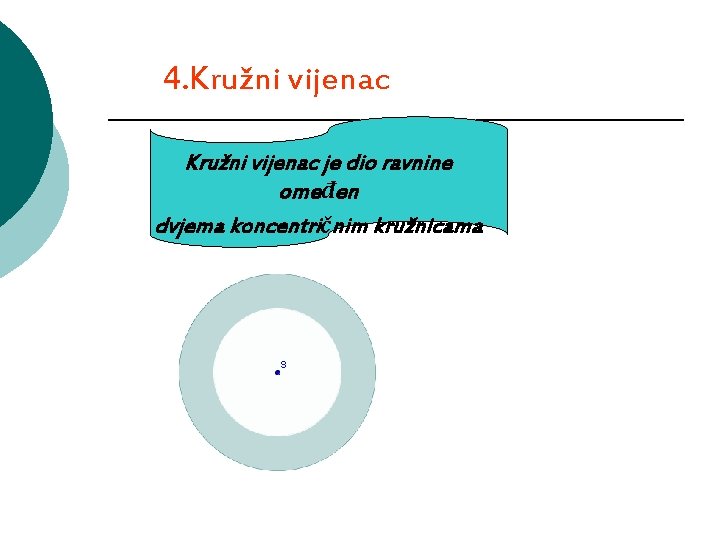
4. Kružni vijenac je dio ravnine omeđen dvjema koncentričnim kružnicama

Obodni i središnji kut ¡ ¡ Središnji je kut dvostruko veći od obodnog kuta nad istim kružnim lukom α =2 · Svi obodni kutovi nad istim kružnim lukom međusobno su jednaki.

Talesov poučak ¡ Svaki obodni kut nad promjerom kružnice je pravi kut.

Tangencijalni četverokut ¡ Četverokut kojemu stranice pripadaju tangentama kružnice nazivamo tangencijalnim četverokutom.

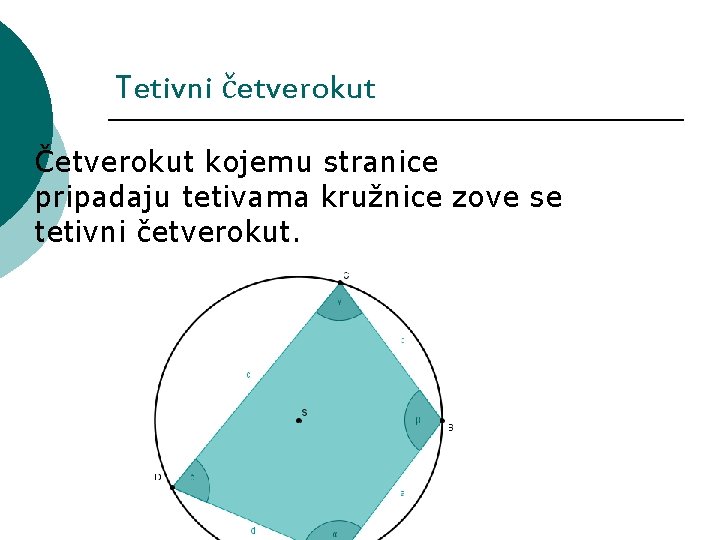
Tetivni četverokut ¡ Četverokut kojemu stranice pripadaju tetivama kružnice zove se tetivni četverokut.

Broj π π, π, π Od tih pilića, a i matematičara do Uskrsa ću i ja pijukati π= opseg kruga : promjer kruga 3. 14 Grčko slovo π -Zaokružen na dvadesetak decimala iznosi 3, 1415926535897932384. Godine 1991. braća Chudnovsky su uz pomoć MZERO računala izračunala broj pi na dvije milijarde dvjesto šezdeset milijuna tristo dvadeset jednu tisuću tristo šezdeset i tri decimale!

14. ožujak- Dan broja π Trenutak u toku dana koji je posebno značajan je u 1 sat i 59 minuta (ili ujutro ili popodne) jer tada broj izgleda ovako: 3. 14 1 59 što je približno broju Pi u 5 znamenki. Ipak, igrajući se brojkama dolazimo do najboljeg dana koji objašnjava broj Pi, a to je: Ožujak 14. , 1592. g. u 6 sati i 53 minute i 59 sekundi (3, 14159265359. . . ), odnosno to bi mogao biti i jedan u budućnosti koji glasi: 3141. g. mjesec svibanj, dan 9. 2 sata 6 minuta 53 sekunde 59 stotinki sekunde. Još jedna važna poveznica sa PI danom je rođendan Alberta Einsteina 14. 03. odnosno 3. 14 oblik datuma u Europi pa ga u novije vrijeme matematičari i fizičari

Opseg kruga Iz pojma broja p može se izvesti formula za opseg kruga. O = 2 rπ

Površina kruga ¡ ¡ Još su se stari Babilonci i Egipćani bavili problemom izračunavanja površine kruga. Pravi izvod formule za površinu kruga dolazi nešto kasnije. Arheolozi su našli vrijednost broja π u zapisima Egipćana Ahmera koji je živio 1800. g. pr. K. i ona je iznosila 3. 1605. Babilonci su bili nešto manje precizni kod izračunavanja broja π i za njegovu vrijednost uzimali su 3. Grci su problem izračunavanja površine kruga preformulirali u problem nalaženja kvadrata koji je ekvivalentan zadanom krugu.

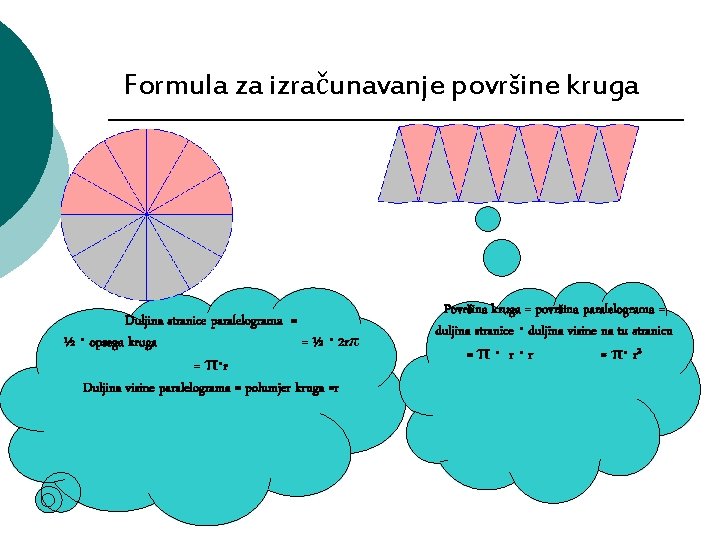
Formula za izračunavanje površine kruga Duljina stranice paralelograma = ½ · opsega kruga = ½ · 2 rπ = π·r Duljina visine paralelograma = polumjer kruga =r Površina kruga = površina paralelograma = duljina stranice · duljina visine na tu stranicu =π· r·r = π· r 2

Duljina kružnog luka Svakom luku kružnice jednoznačno je pridružen kut s vrhom u središtu kružnice. l je oznaka duljine luka za kut α

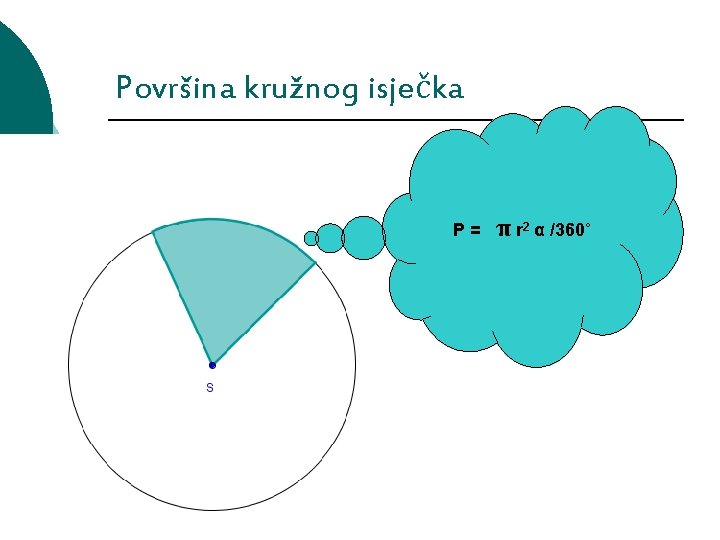
Površina kružnog isječka P= π r 2 α /360˚

Krugovi u sportu

Literatura: 1) MATEMATIKA 7 Zvonimir Šikić, Vesna Draženović- Žitko, Maja Marić, Luka Krnić 2) SJECIŠTE, matematika za 7. razred, udžbenik i zbirka zadataka, 3) TAJNI ZADATAK 007 Renata Svedrec, Nikol Radović, Tanja Saucha, Ivana Kokić 4) MATEMATIKA 7, Boško Jagodić, Nikola Sarapa 5) Internet

Napravili: ¡ Zvonimir Bartol ¡ Antonio Drvenkar ¡ Mihael Juršetić ¡ Matija Levatić ¡ Kristijan Tvorić 7. b. Razred I. Osnovne škole Vrbovec ¡ ¡