Realni brojevi Brojevi Prirodni brojevi 1 2 3

Realni brojevi

Brojevi. . .

Prirodni brojevi • 1, 2, 3, 4, 5, 6, 7, 8, . . . • Prebrajanje • Skup prirodnih brojeva N • a+b • a-b

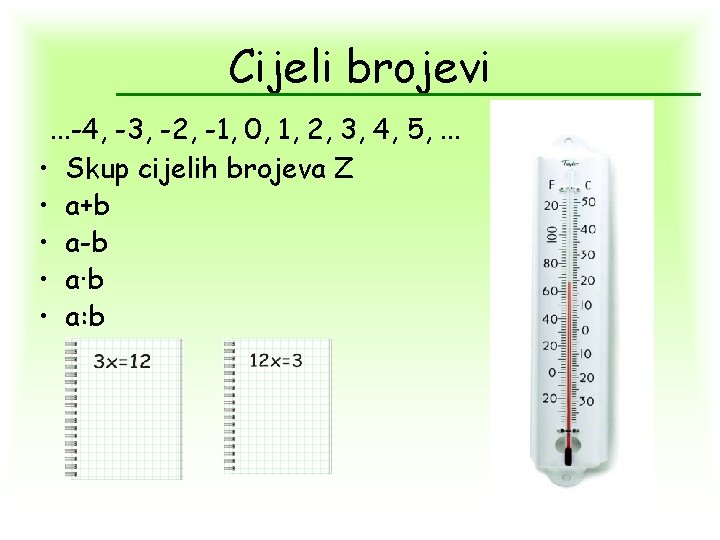
Cijeli brojevi. . . -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, . . . • Skup cijelih brojeva Z • a+b • a-b • a·b • a: b

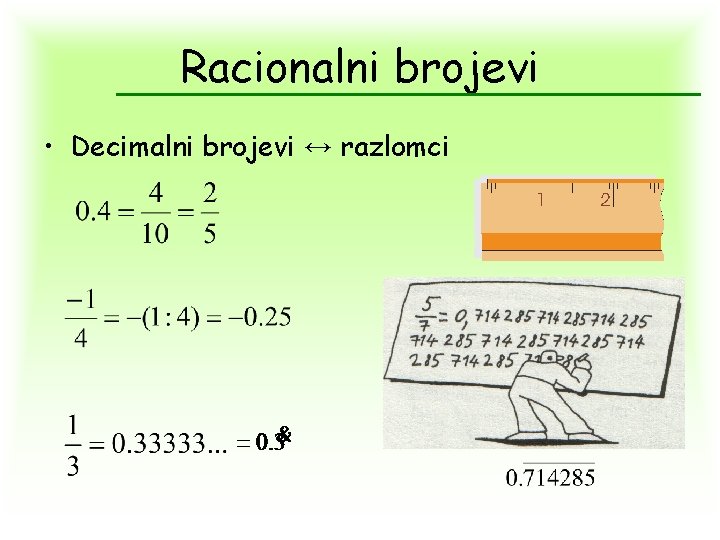
Racionalni brojevi • Decimalni brojevi ↔ razlomci

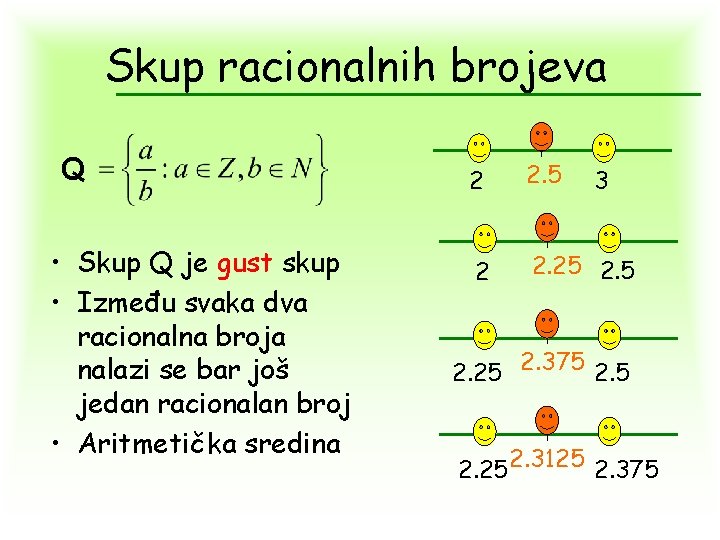
Skup racionalnih brojeva Q • Skup Q je gust skup • Između svaka dva racionalna broja nalazi se bar još jedan racionalan broj • Aritmetička sredina 2 2. 5 2 2. 25 2. 5 3 2. 25 2. 375 2. 25 2. 3125 2. 375

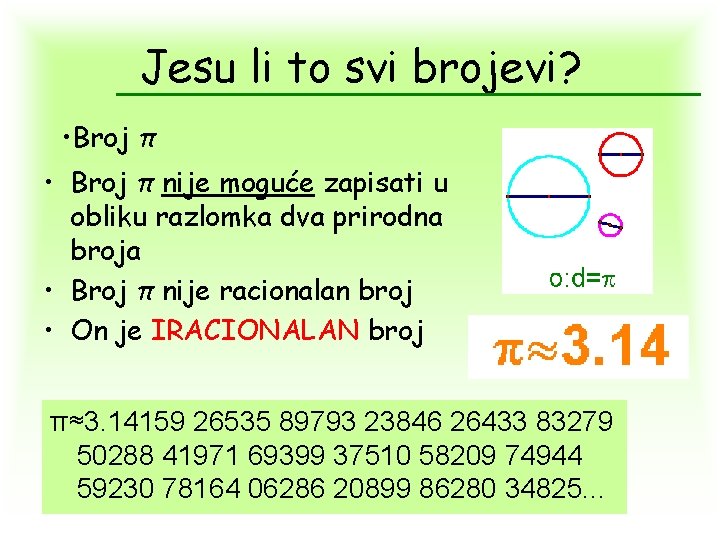
Jesu li to svi brojevi? • Broj π nije moguće zapisati u obliku razlomka dva prirodna broja • Broj π nije racionalan broj • On je IRACIONALAN broj π≈3. 14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825. . .

Jesu li to svi brojevi? • Kolika je duljina dijagonale kvadrata stranice 1 cm? • √ 2 nije moguće zapisati u obliku razlomka dva prirodna broja • √ 2 nije racionalan broj • √ 2 je IRACIONALAN broj

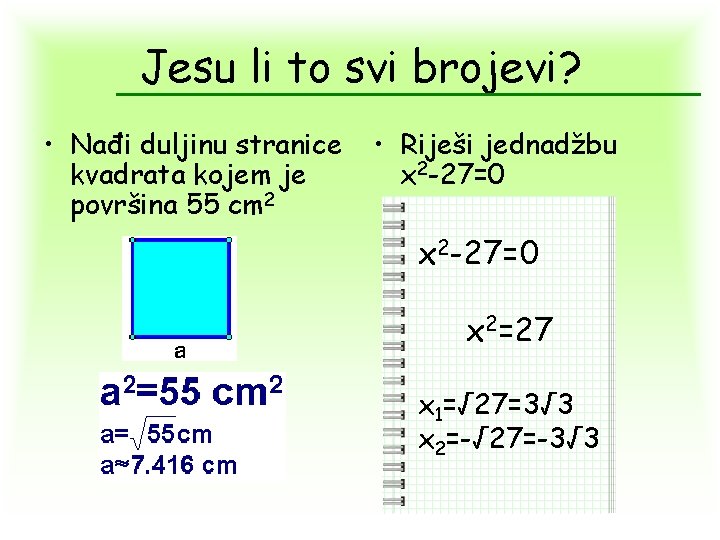
Jesu li to svi brojevi? • Nađi duljinu stranice kvadrata kojem je površina 55 cm 2 • Riješi jednadžbu x 2 -27=0 x 2=27 x 1=√ 27=3√ 3 x 2=-√ 27=-3√ 3

Jesu li to svi brojevi? • Racionalni brojevi • Iracionalni brojevi: π, √ 2, √ 55, 3√ 3, -3√ 3 Jesu li to svi brojevi? x 2+1=0

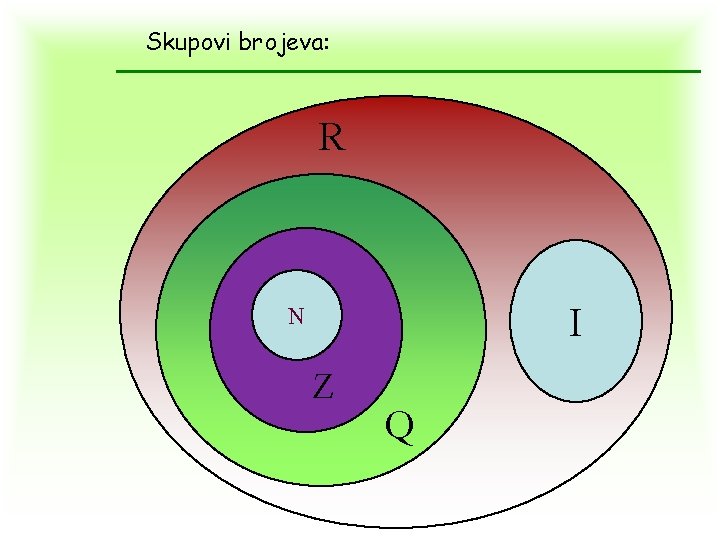
Skupovi brojeva: R I N Z Q

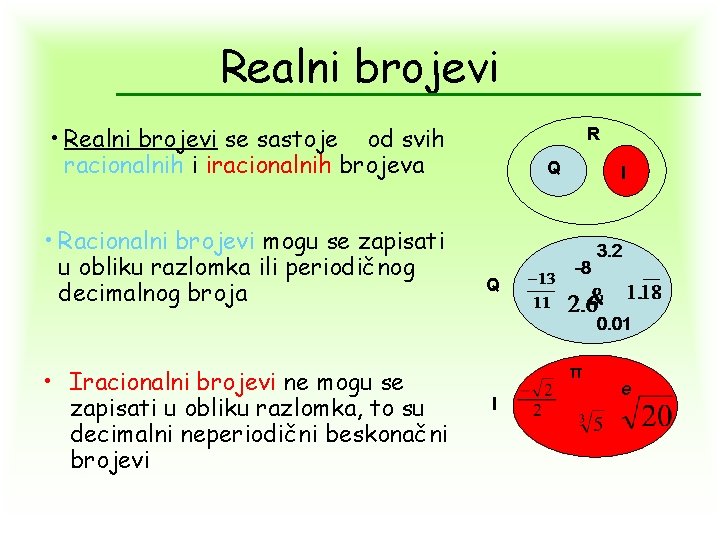
Realni brojevi • Realni brojevi se sastoje od svih racionalnih i iracionalnih brojeva • Racionalni brojevi mogu se zapisati u obliku razlomka ili periodičnog decimalnog broja • Iracionalni brojevi ne mogu se zapisati u obliku razlomka, to su decimalni neperiodični beskonačni brojevi R Q I Q π I e

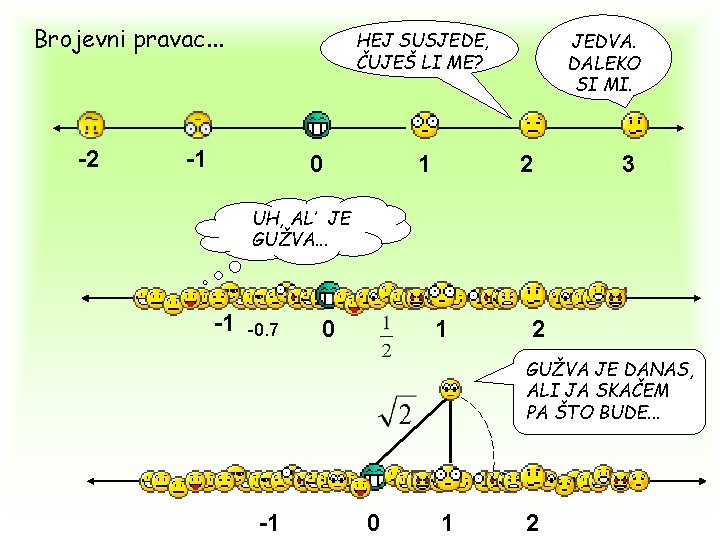
Brojevni pravac. . . -2 HEJ SUSJEDE, ČUJEŠ LI ME? -1 0 1 JEDVA. DALEKO SI MI. 2 3 UH, AL’ JE GUŽVA. . . -1 -0. 7 0 1 2 GUŽVA JE DANAS, ALI JA SKAČEM PA ŠTO BUDE. . . -1 0 1 2

Povijesne crtice • Pitagorejci: racionalni brojevi (omjer) • Hipas: iracionalni brojevi (√ 2) • Arhimed: približno √ 3, π. . . • Descartes 17. st: naziv “realni brojevi” • Ruđer Bošković 18. st: iracionalni - “neizrazivi brojevi”