Racionalni brojevi Ponavljanje na poetku 8 razreda Provjerimo

Racionalni brojevi Ponavljanje na početku 8. razreda Provjerimo svoje znanje da vidimo pravo stanje…

Koje smo vrste brojeva upoznali prethodnih godina i što koji opisuju? - prirodni brojevi 1, 2, 3, 4, 5, 6… - cijeli brojevi 1, 2, 3, 4…, 0, -1, -2, -3, -4… - razlomci - mješoviti brojevi - decimalni brojevi 5. 7, -0. 304 … - racionalni brojevi - razlomci i svi brojevi koje možemo pretvoriti u razlomke

Koje smo vrste brojeva upoznali prethodnih godina i što koji opisuju? - prirodni brojevi 1, 2, 3, 4, 5, 6… - cijeli brojevi 1, 2, 3, 4…, 0, -1, -2, -3, -4… - razlomci - mješoviti brojevi - decimalni brojevi 5. 7, -0. 304 … RACIONALNI BROJEVI

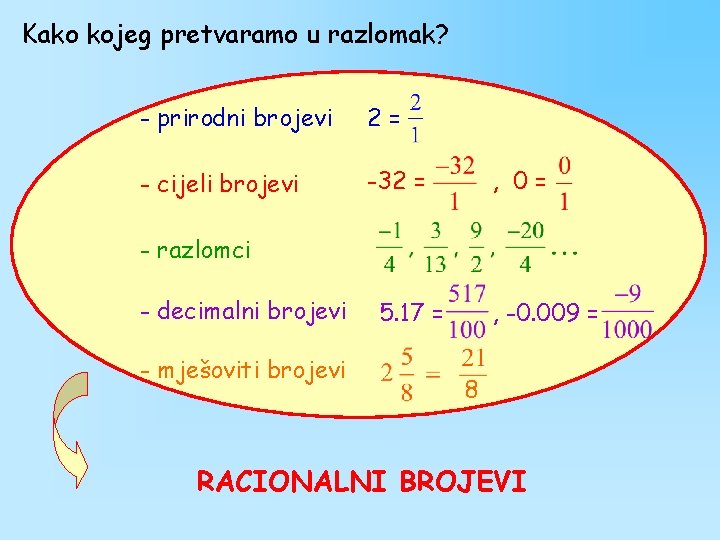
Kako kojeg pretvaramo u razlomak? - prirodni brojevi 2= - cijeli brojevi -32 = , 0= - razlomci - decimalni brojevi - mješoviti brojevi 5. 17 = , -0. 009 = 8 RACIONALNI BROJEVI

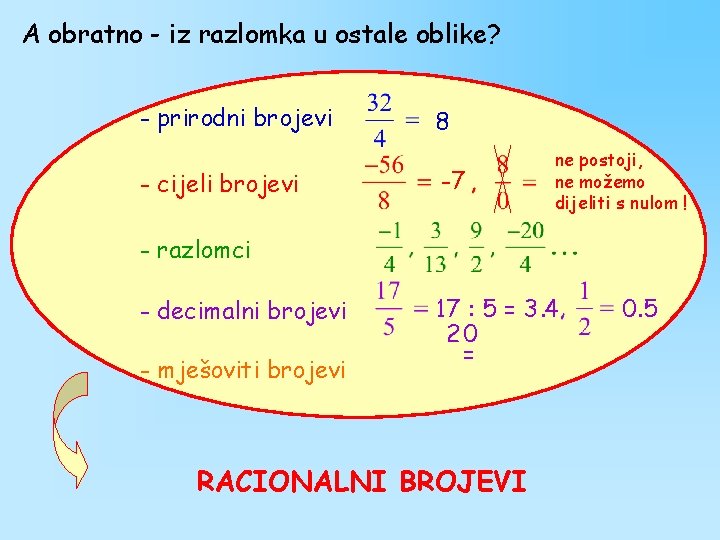
A obratno - iz razlomka u ostale oblike? - prirodni brojevi - cijeli brojevi 8 -7 ne postoji, ne možemo dijeliti s nulom ! - razlomci - decimalni brojevi - mješoviti brojevi 17 : 5 = 3. 4 20 = RACIONALNI BROJEVI 0. 5

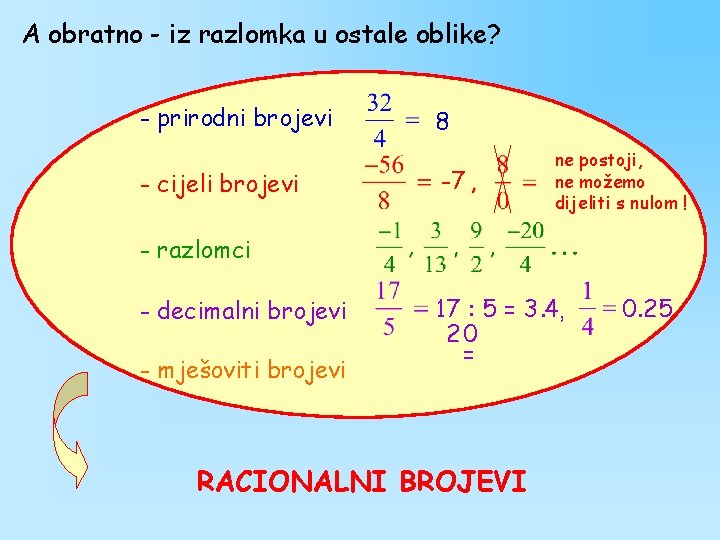
A obratno - iz razlomka u ostale oblike? - prirodni brojevi - cijeli brojevi 8 -7 ne postoji, ne možemo dijeliti s nulom ! - razlomci - decimalni brojevi - mješoviti brojevi 17 : 5 = 3. 4 , 20 = RACIONALNI BROJEVI 0. 25

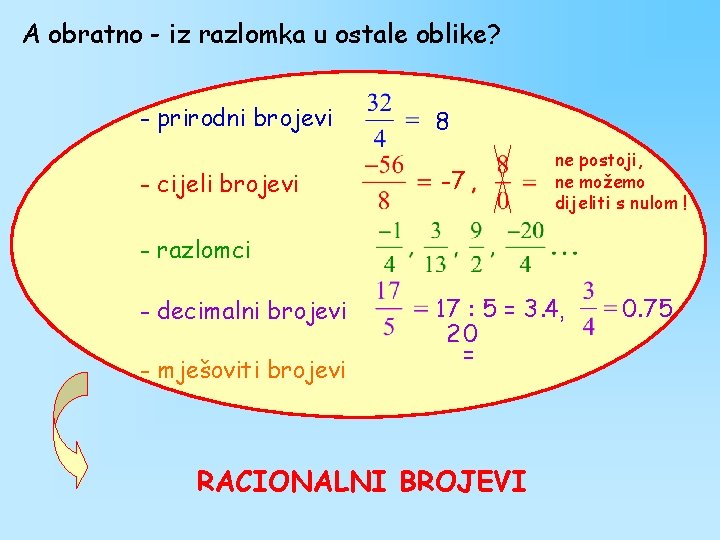
A obratno - iz razlomka u ostale oblike? - prirodni brojevi - cijeli brojevi 8 -7 ne postoji, ne možemo dijeliti s nulom ! - razlomci - decimalni brojevi - mješoviti brojevi 17 : 5 = 3. 4 , 20 = RACIONALNI BROJEVI 0. 75

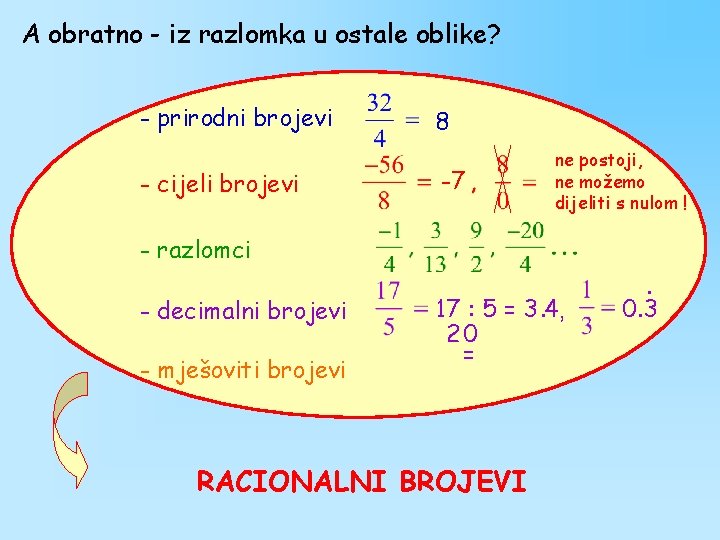
A obratno - iz razlomka u ostale oblike? - prirodni brojevi - cijeli brojevi 8 -7 ne postoji, ne možemo dijeliti s nulom ! - razlomci - decimalni brojevi - mješoviti brojevi 17 : 5 = 3. 4 , 20 = RACIONALNI BROJEVI . 0. 3

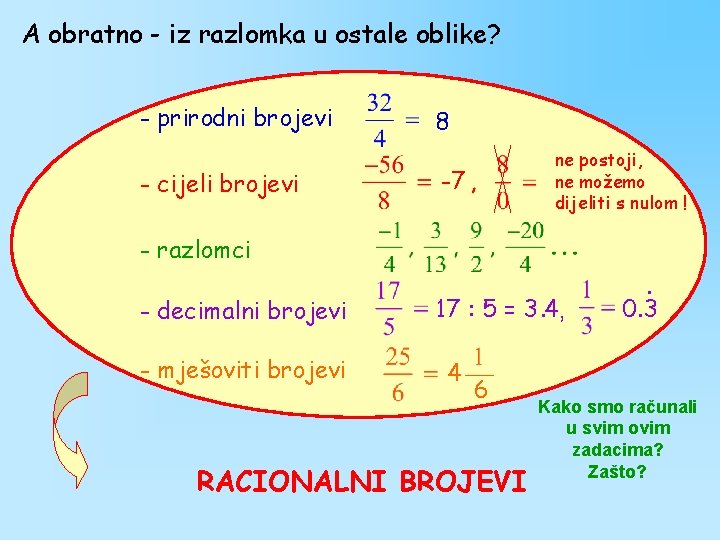
A obratno - iz razlomka u ostale oblike? - prirodni brojevi - cijeli brojevi 8 ne postoji, ne možemo dijeliti s nulom ! -7 - razlomci - decimalni brojevi - mješoviti brojevi 17 : 5 = 3. 4 , 4 6 RACIONALNI BROJEVI . 0. 3 Kako smo računali u svim ovim zadacima? Zašto?

Rješavanjem prošlih zadataka ponovili smo koje su veze među različitim vrstama brojeva. To je bio "pogled odozgo". Sad krenimo na konkretnija ponavljanja za svaki skup brojeva posebno. Krećemo s brojevima koje poznajete još iz nižih razreda, a to su. . .

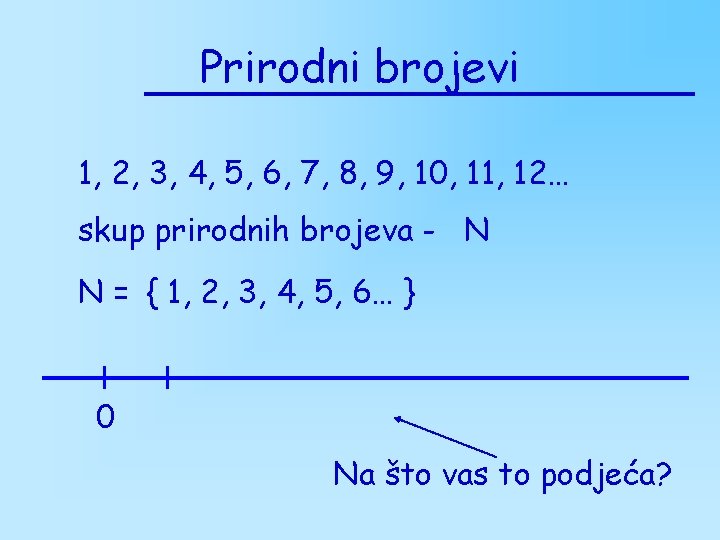
Prirodni brojevi 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12… skup prirodnih brojeva - N N = { 1, 2, 3, 4, 5, 6… } 0 Na što vas to podjeća?

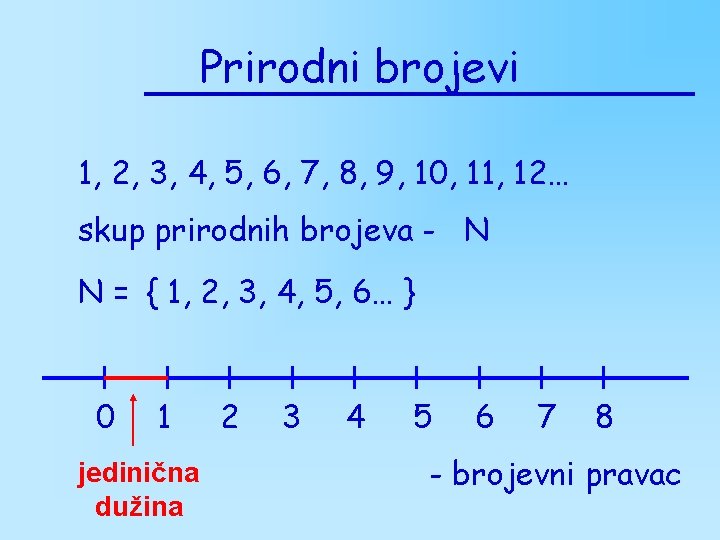
Prirodni brojevi 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12… skup prirodnih brojeva - N N = { 1, 2, 3, 4, 5, 6… } 0 1 jedinična dužina 2 3 4 5 6 7 8 - brojevni pravac

Prirodni brojevi Koje smo sve računske operacije radili u skupu N? - zbrajanje - oduzimanje 7 + 6 = 6 + 7 7 ? 6 = 6 ? 7 - množenje - dijeljenje komutativnost zbrajanja komutativnost ?

Prirodni brojevi Koje smo sve računske operacije radili u skupu N? - zbrajanje - oduzimanje 7 + 6 = 6 + 7 7 · 6 = 6 · 7 (1+4)+2 = 1+(4+2) (1? 4)? 2 = - množenje - dijeljenje komutativnost zbrajanja komutativnost množenja asocijativnost zbrajanja

Prirodni brojevi Koje smo sve računske operacije radili u skupu N? - zbrajanje - oduzimanje 7 + 6 = 6 + 7 7 · 6 = 6 · 7 - množenje - dijeljenje komutativnost zbrajanja komutativnost množenja (1+4)+2 = 1+(4+2) asocijativnost zbrajanja (1· 4)· 2 = 1·(4· 2) asocijativnost množenja 5·(2+4) = 5· 2+5· 4 distributivnost množenja prema zbrajanju

Da li navedena svojstva vrijede samo kad računamo s prirodnim brojevima ili i inače? - Vrijede uvijek! Sad krenimo na cijele brojeve. . .

Cijeli brojevi 1, 2, 3, 4, 5…, 0, -1, -2, -3, -4, -5… skup cijelih brojeva - Z Z = { … -4, -3, -2, -1, 0, 1, 2, 3, 4… } -4 -3 -2 -1 0 1 2 3 4 Kako dalje?

Cijeli brojevi Usporedi sljedeća dva broja: 23 > 14 -12 < 5 -30 < -20 5 4 3 2 1 0 -1 -2 -3 -4 -5 v e ć i m a nj i

Cijeli brojevi Kako zbrajamo cijele brojeve? - ako imaju jednake predznake: - predznak prepišemo - apsolutne vrijednosti zbrojimo - ako imaju različite predznake: - prepišemo predznak od većega - apsolutne vrijednosti oduzmemo

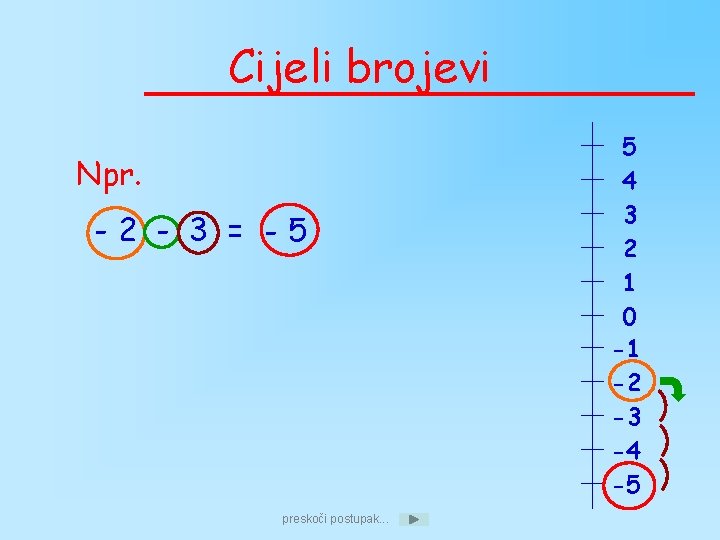
Cijeli brojevi Npr. -2 - 3 = -5 preskoči postupak. . . 5 4 3 2 1 0 -1 -2 -3 -4 -5

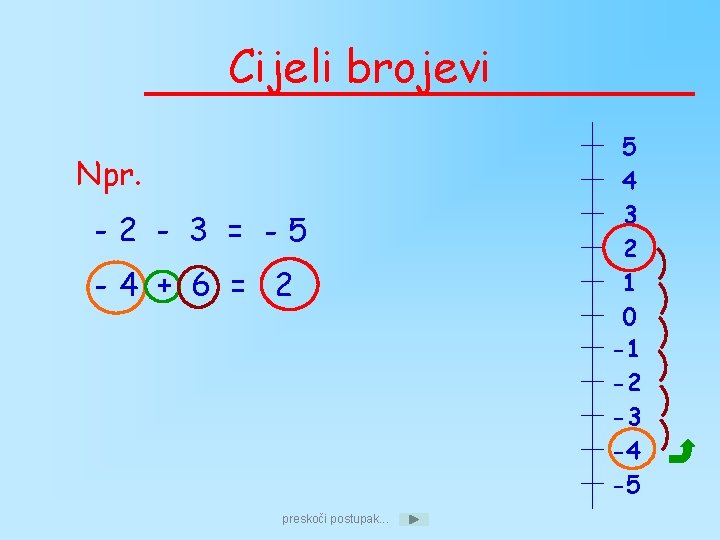
Cijeli brojevi Npr. -2 - 3 = -5 -4 + 6 = 2 preskoči postupak. . . 5 4 3 2 1 0 -1 -2 -3 -4 -5

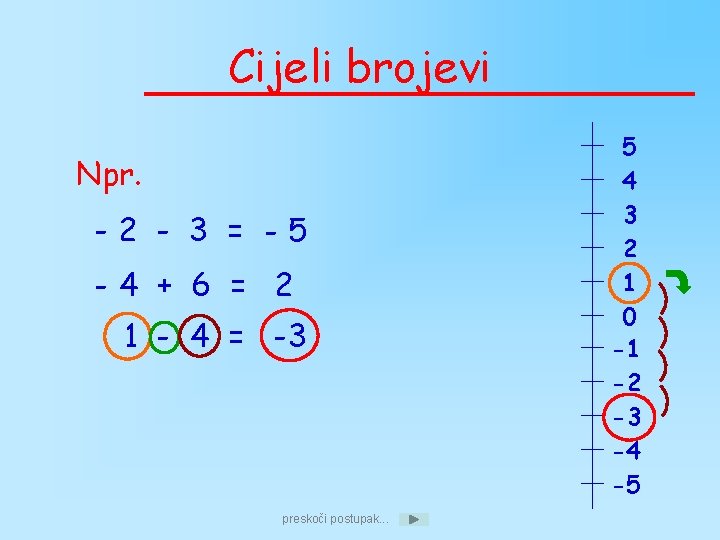
Cijeli brojevi Npr. -2 - 3 = -5 -4 + 6 = 2 1 - 4 = -3 preskoči postupak. . . 5 4 3 2 1 0 -1 -2 -3 -4 -5

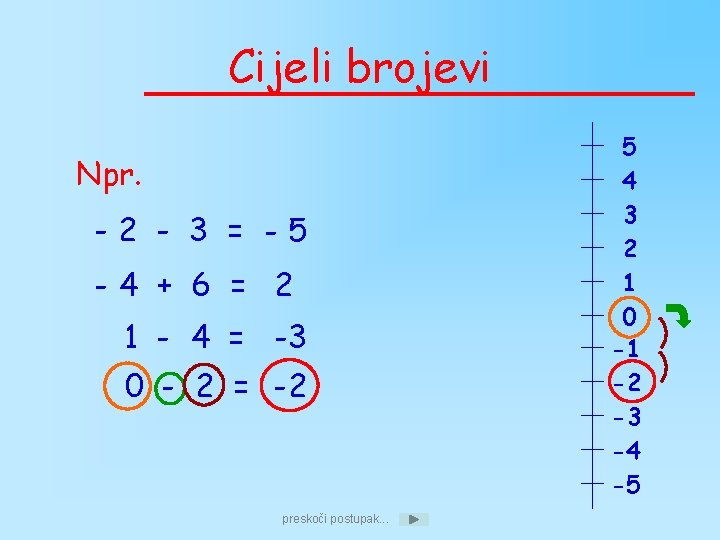
Cijeli brojevi Npr. -2 - 3 = -5 -4 + 6 = 2 1 - 4 = -3 0 - 2 = -2 preskoči postupak. . . 5 4 3 2 1 0 -1 -2 -3 -4 -5

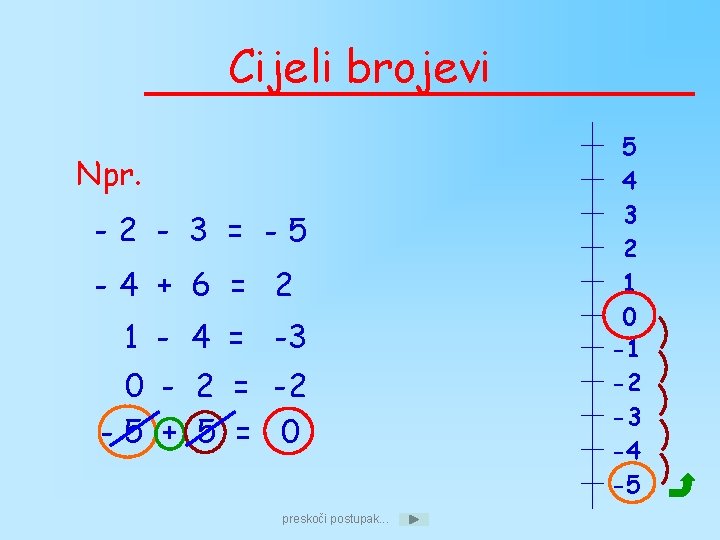
Cijeli brojevi Npr. -2 - 3 = -5 -4 + 6 = 2 1 - 4 = -3 0 - 2 = -2 -5 + 5 = 0 preskoči postupak. . . 5 4 3 2 1 0 -1 -2 -3 -4 -5

Cijeli brojevi Npr. - 7 - 5 ___ + 8 - 1 +___ 3 = 11 - 13 = = -2 37 - 55_____ + 128 - 55 - 37 = 128 - 110 = = 18

Cijeli brojevi Kako množimo i dijelimo cijele brojeve? Npr. -6 · (-4) · (-1) = - 24 -2 · (-5) · 4 · (-1) · (-3) = +120 Zašto su neki brojevi u zagradama? Paran broj minusa daje +. Neparan broj minusa daje -.

Cijeli brojevi A što ćemo s ovim zagradama: -3 + (-7) = -3 - 7 = - 10 -6 - (-8) = -6 + 8 = 2 8 - (+9) = 8 - 9 = - 1 Ako je ispred zagrade +, da sve on nam govori. . . iz zagrade samo prepišemo. Ako je ispred zagrade -, da svakom on nam govori. . . -32 - 4 - (-32) + (-4) = iz zagrade promijenimo = -32 - 4 + 32 - 4 = - 8 predznak.

To bi bilo sve!!! Nadam se da je bilo zanimljivo i korisno! Složenije zadatke s više računskih operacija i sa zagradama rješavat ćemo u bilježnice. . .

Prezentaciju napravila: Antonija Horvatek rujan 2006.

Ovaj materijal možete koristiti u nastavi, tj. u radu s učenicima. U istu svrhu dozvoljeno je mijenjati ga i prilagoditi svojim potrebama. Za svako korištenje materijala koje nije rad s učenicima, npr. za objavljivanje materijala ili dijelova materijala u časopisima, udžbenicima, na CD-ima. . . , za korištenje na predavanjima, radionicama. . . , potrebno je tražiti i dobiti dozvolu autorice, te vezano uz objavu materijala navesti ime autorice (ako dozvolu dobijete). Ukoliko na bilo koji način koristite moje materijale, bit će mi drago ako dobijem povratnu informaciju, Vaše primjedbe, komentare. . . Antonija Horvatek Matematika na dlanu http: //www. antonija-horvatek. from. hr/