Information Theory and Neural Coding Ph D Oral

Information Theory and Neural Coding Ph. D Oral Examination November 29, 2001 Albert E. Parker Complex Biological Systems Department of Mathematical Sciences Center for Computational Biology Montana State University Collaborators: Tomas Gedeon Alexander Dimitrov John P. Miller Zane Aldworth

Outline Ø The Problem Ø Our Approach § Build a Model: Probability and Information Theory § Use the Model: Optimization Ø Results Ø Bifurcation Theory Ø Future Work

Why are we interested in neural coding? • We are computationalists: All computations underlying an animal's behavioral decisions are carried out within the context of neural codes. • Neural prosthetics: to enable a silicon device (artificial retina, cochlea, etc. ) to interface with the human nervous system.

Neural Coding and Decoding The Problem: Determine a coding scheme: How does neural activity represent information about environmental stimuli? Demands: • An animal needs to recognize the same object on repeated exposures. Coding has to be deterministic at this level. • The code must deal with uncertainties introduced by the environment and neural architecture. Coding is by necessity stochastic at this finer scale. Major Obstacle: The search for a coding scheme requires large amounts of data

How to determine a coding scheme? Idea: Model a part of a neural system as a communication channel using Information Theory. This model enables us to: • Meet the demands of a coding scheme: o Define a coding scheme as a relation between stimulus and neural response classes. o Construct a coding scheme that is stochastic on the finer scale yet almost deterministic on the classes. • Deal with the major obstacle: o Use whatever quantity of data is available to construct coarse but optimally informative approximations of the coding scheme. o Refine the coding scheme as more data becomes available.

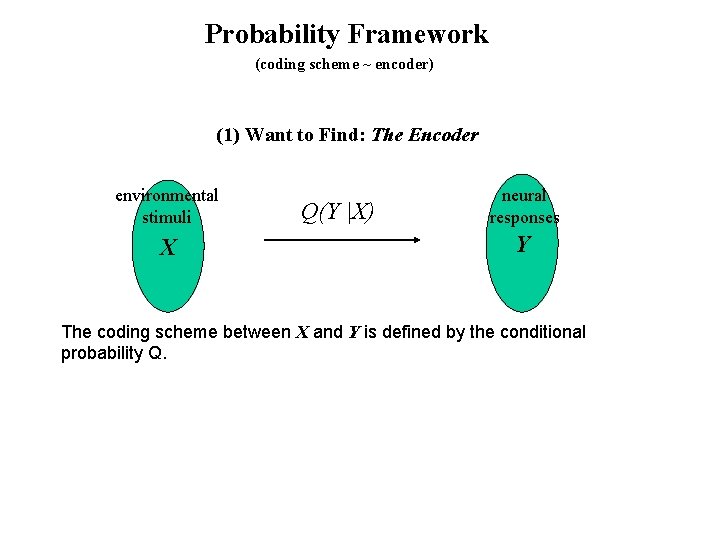
Probability Framework (coding scheme ~ encoder) (1) Want to Find: The Encoder environmental stimuli X Q(Y |X) neural responses Y The coding scheme between X and Y is defined by the conditional probability Q.

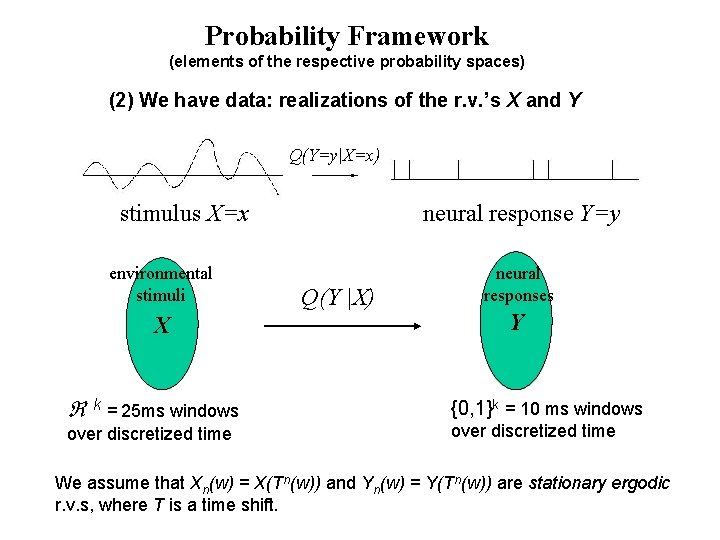
Probability Framework (elements of the respective probability spaces) (2) We have data: realizations of the r. v. ’s X and Y Q(Y=y|X=x) stimulus X=x environmental stimuli X k = 25 ms windows over discretized time neural response Y=y Q(Y |X) neural responses Y {0, 1}k = 10 ms windows over discretized time We assume that Xn(w) = X(Tn(w)) and Yn(w) = Y(Tn(w)) are stationary ergodic r. v. s, where T is a time shift.

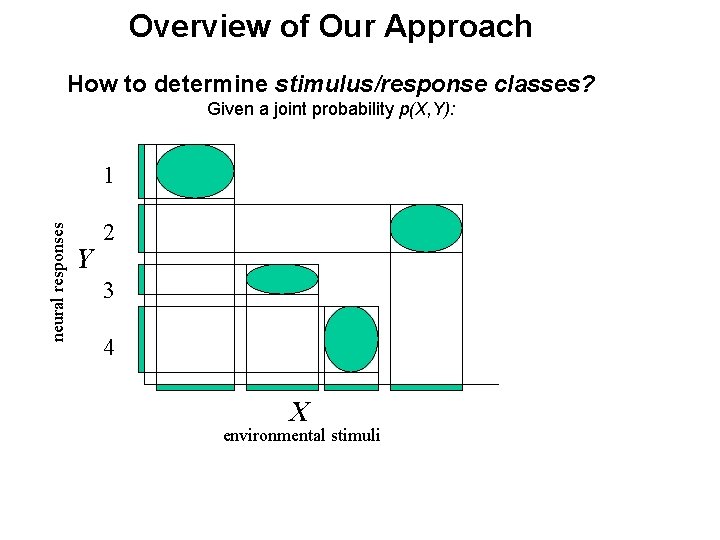
Overview of Our Approach How to determine stimulus/response classes? Given a joint probability p(X, Y): neural responses 1 Y 2 3 4 X environmental stimuli

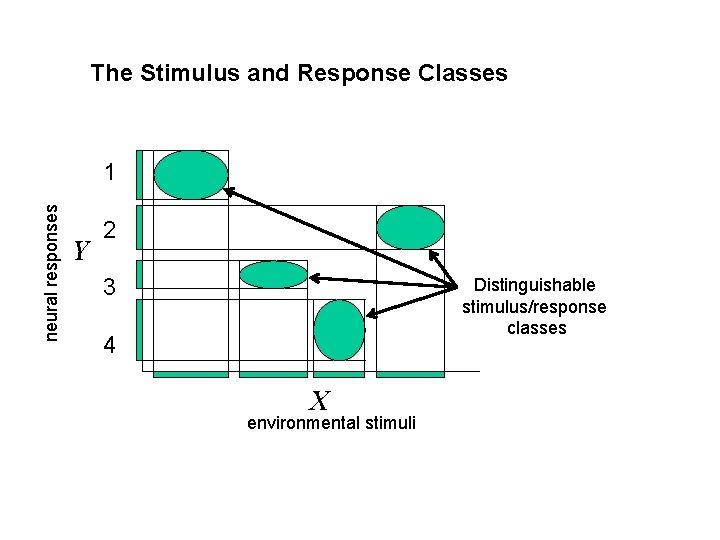
The Stimulus and Response Classes neural responses 1 Y 2 3 Distinguishable stimulus/response classes 4 X environmental stimuli

Information Theory The Foundation of the Model • A signal x is produced by a source (r. v. ) X with a probability p(X=x). A signal y is produced by another source Y with probability p(Y=y). • A communication channel is a relation between two r. v. ’s X and Y. It is described by the (finite) conditional probability or quantizer: Q(Y | X). • Entropy: the uncertainty or self information of a r. v. • Conditional Entropy: • Mutual Information: the amount of information that one r. v. contains about another r. v.

Why Information Theory? The entropy and mutual information of the data asymptotically approach the true population entropy and mutual information respectively. Shannon Mc. Millan Breiman Theorem (iid case) If are i. i. d. , then Proof: Let Yi=log p(Xi ) Large Numbers. are i. i. d. . The theorem follows from the Strong Law of This result holds if is a stationary ergodic sequences as well. This is important for us since our data is not i. i. d. , but we do assume that X and Y are stationary ergodic.

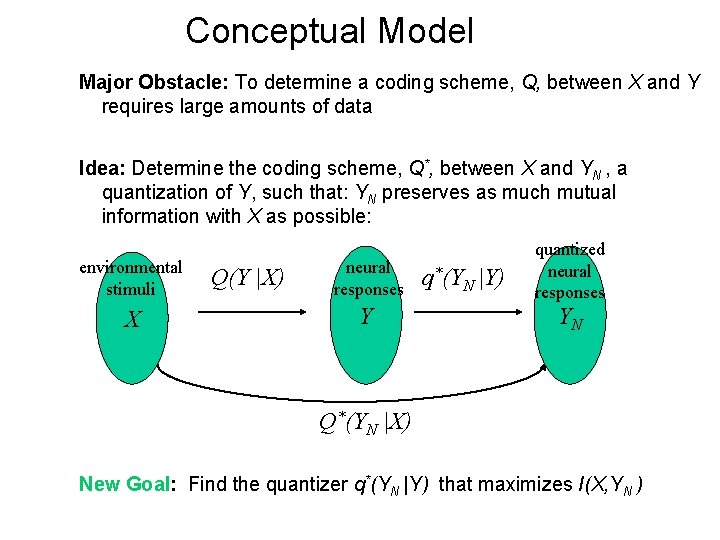
Conceptual Model Major Obstacle: To determine a coding scheme, Q, between X and Y requires large amounts of data Idea: Determine the coding scheme, Q*, between X and YN , a quantization of Y, such that: YN preserves as much mutual information with X as possible: environmental stimuli X Q(Y |X) neural responses Y q*(YN |Y) quantized neural responses YN Q*(YN |X) New Goal: Find the quantizer q*(YN |Y) that maximizes I(X, YN )

Mathematical Model We search for the maximizer q*(YN|Y) which satisfies maxq H(YN |Y) constrained by I(X, YN ) = Imax : = maxq I(X, YN) The feasible region assures that q*(YN|Y) is a true conditional probability. y y is a product of simplices (each simplex is a discrete probability space)

Justification We begin our search for the maximizer q*(YN|Y) by solving q* = argmaxq I(X, YN ) ❶ ❷ If there are multiple solutions to , then, by Jayne's maximum entropy principle, we take the one that maximizes the entropy maxq H(YN |Y) constrained by I(X, YN ) = Imax In order to solve , use the method of lagrange multipliers to get maxq H(YN |Y) + I(X, YN ) ❹ Annealing: In practice, we increment in small steps to . For each , we solve q* = argmaxq H(YN |Y) + I(X, YN ) Note that lim q* = q* from .

Some nice properties of the model ü The information functions are nice. Theorem 1 H(YN |Y) is concave, I(X, YN ) is convex. ü is really nice. Lemma 2 is the convex hull of vertices ( ). ü We can reformulate as two different optimization problems Theorem 3 An equivalent problem to is to solve q*(YN|Y) = argmaxq vertices( ) I(X, YN ) Proof: This result follows from Theorem 1 and Lemma 2. Corollary 4 The extrema of lie on the vertices of . Theorem 5 If q*M is the maximizer of constrained by I(X, YN ) = Imax then q* = 1/M q*M, where Proof: By Theorem 3 and the fact that M is the convex hull of vertices( M)

Optimization Schemes Goal: Build a sequence . ¨ Annealing: q* = argmaxq H(YN |Y) + I(X, YN ) v Augmented Lagrangian Method v Implicit solution: Set . Solve implicitly for q: Drawback: current choice of is ad hoc. 1 ¨ Vertex Search Algorithm: maxq vertices( ) I(X, YN ) Drawback: |vertices ( )| = N|Y| 2 3

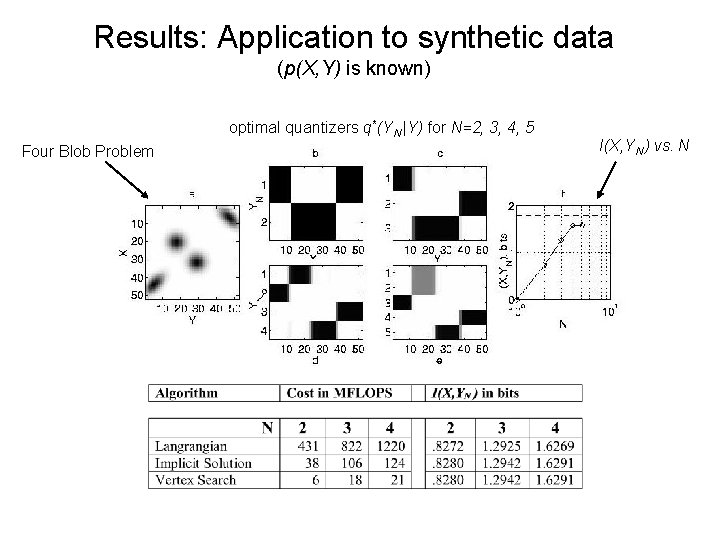
Results: Application to synthetic data (p(X, Y) is known) optimal quantizers q*(YN |Y) for N=2, 3, 4, 5 Four Blob Problem I(X, YN ) vs. N

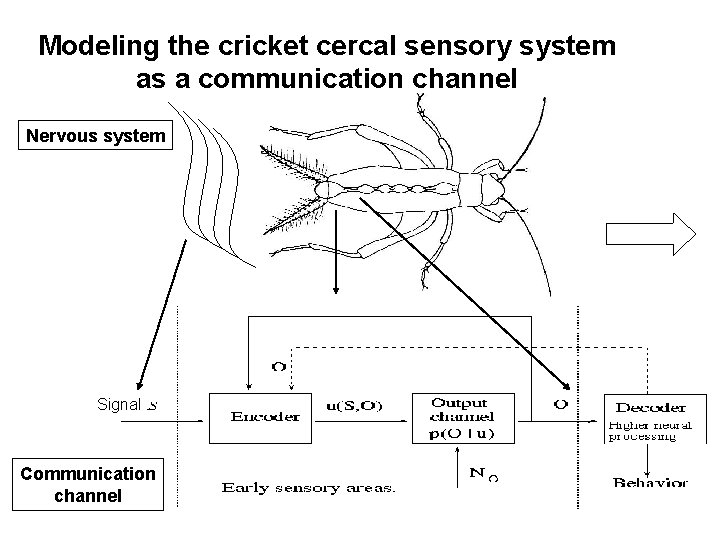
Modeling the cricket cercal sensory system as a communication channel Nervous system Signal Communication channel

Why the cricket? • The structure and details of the cricket cercal sensory system are well known. • All of the neural activity (about 20 neurons) which encode the wind stimuli can be measured. • Other sensory systems (e. g. mammalian visual cortex) consist of millions of neurons, which are impossible (today) to measure in totality.

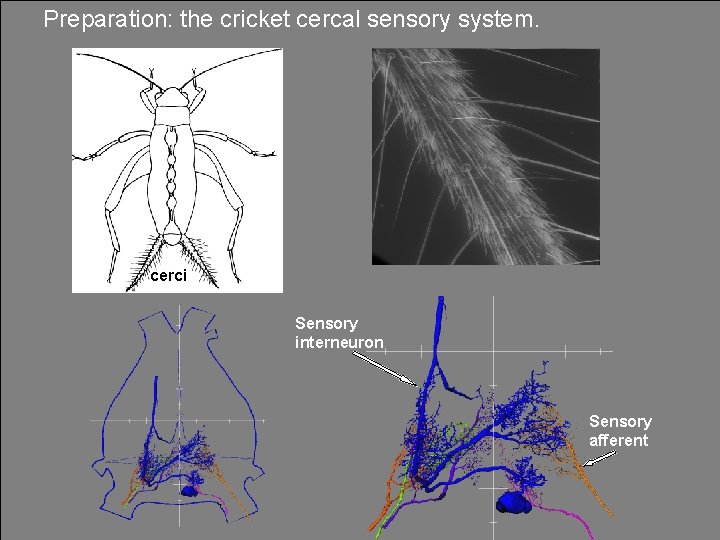
Preparation: the cricket cercal sensory system. cerci Sensory interneuron Sensory afferent

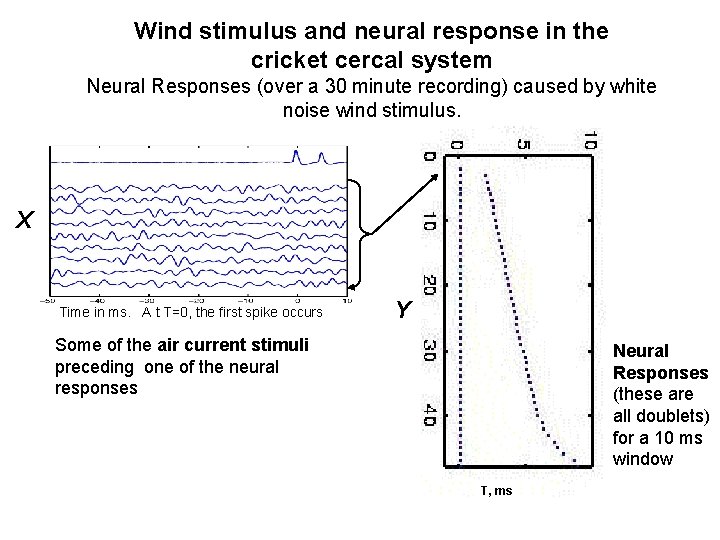
Wind stimulus and neural response in the cricket cercal system Neural Responses (over a 30 minute recording) caused by white noise wind stimulus. X Time in ms. A t T=0, the first spike occurs Y Some of the air current stimuli preceding one of the neural responses Neural Responses (these are all doublets) for a 10 ms window T, ms

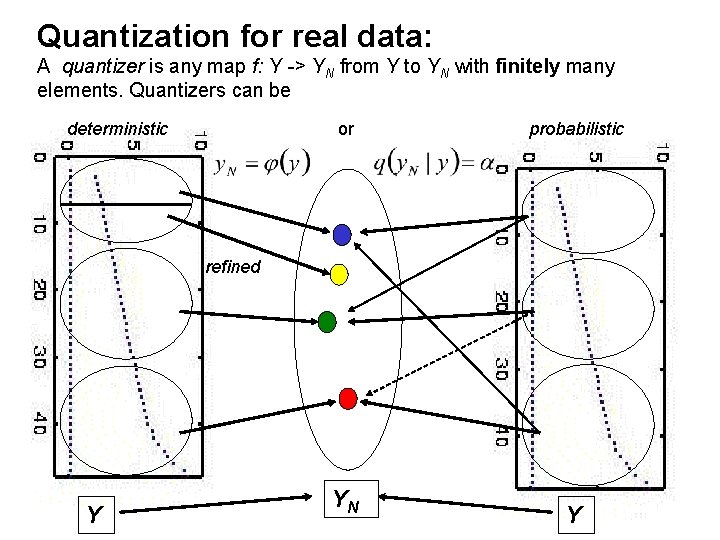
Quantization for real data: A quantizer is any map f: Y -> YN from Y to YN with finitely many elements. Quantizers can be deterministic or probabilistic refined Y YN Y

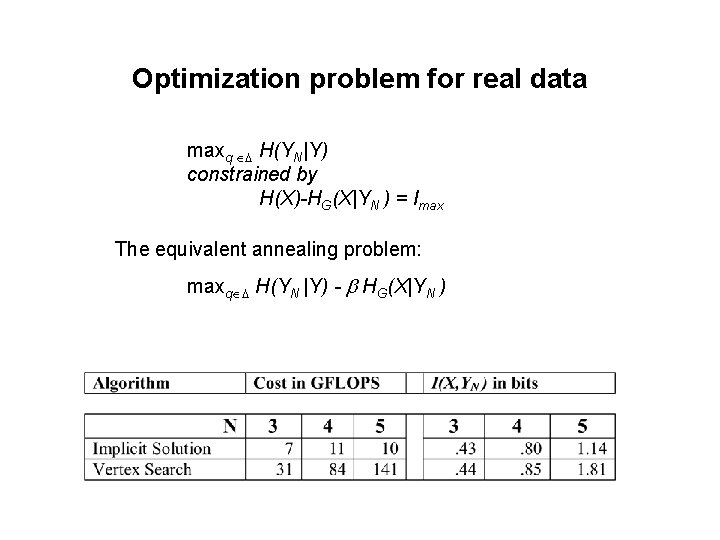
Optimization problem for real data maxq H(YN|Y) constrained by H(X)-HG(X|YN ) = Imax The equivalent annealing problem: maxq H(YN |Y) - HG(X|YN )

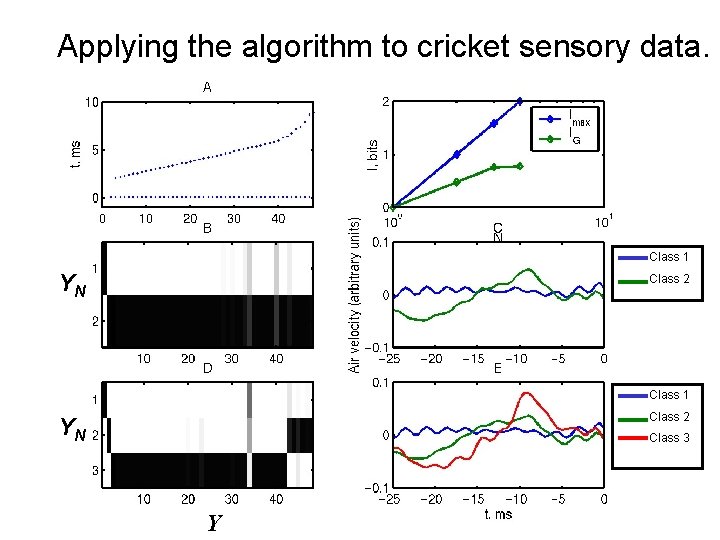
Applying the algorithm to cricket sensory data. Class 1 YN Class 2 Class 1 Class 2 YN Class 3 Y

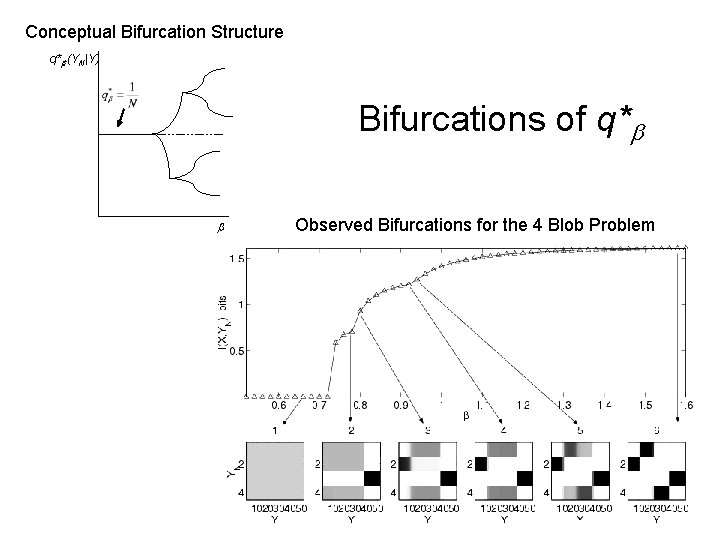
Investigating the Bifurcation Structure Goal: To efficiently solve q* = argmaxq H(YN |Y) + I(X, YN ) for each as . Idea: Choose wisely. Method: Study the equilibria of the flow which are precisely the maximizers q* . The first equilibrium is q* = 0 1/N. ü Search for bifurcations of the equilibria ü Use numerical continuation to choose q* (YN|Y) Conjecture: There are only pitchfork bifurcations

Conceptual Bifurcation Structure q* (YN|Y) Bifurcations of q* Observed Bifurcations for the 4 Blob Problem

Other Applications Solving problems of the form x* = argmax H(Y | X) + D are common in many fields: • • Clustering Compression and communications (GLA) Pattern recognition (ISODATA, K-mean) Regression

Future Work • Bifurcation structure o Capitalize on the symmetries of q* (Singularity and Group Theory) • Annealing Algorithm Improvement o Perform optimization only at where bifurcations occur o Use Numerical Continuation to choose o Implicit Solution method qn+1 = f (qn , ) converges reliably and quickly. Why? Investigate the superattracting directions. • Perform optimization over a product of M-simplices • Joint Quantization o Quantize X and Y simultaneously • Better maximum entropy models for real data. • Compare our method to others.