HKOI 2009 Training Advanced Group DYNAMIC PROGRAMMING II

HKOI 2009 Training (Advanced Group) DYNAMIC PROGRAMMING II (Reference: Powerpoint of Dynamic Programming II, HKOI Training 2005, by Liu Chi Man, cx)

Review � Recurrence relation � Dynamic programming �State & Recurrence Formula �Optimal substructure �Overlapping subproblems 2

Outline � Dimension reduction (memory) � “Ugly” optimal value functions � DP on tree structures � Two-person games 3

Dimension reduction Reduce the space complexity by one or more dimensions � “Rolling” array � Recall: Longest Common Subsequence (LCS) � Base conditions and recurrence relation: � �Fi, 0 = 0 for all i �F 0, j = 0 for all j �Fi, j = Fi-1, j-1 + 1 max{ Fi-1, j , Fi, j-1 } (if A[i] = B[j]) (otherwise) 4

Dimension Reduction � A: stxc, B: sicxtc 0 1 2 3 4 5 6 0 0 0 0 1 0 1 1 1 2 0 1 1 2 2 3 0 1 1 1 2 2 2 4 0 1 1 2 2 2 3 0 1 2 3 4 5 6 0 2 4 0 0 1 0 1 2 0 2 3 1 3 0 1 1 2 1 2 5

Dimension Reduction We may discard old table entries if they are no longer needed Instead of “rolling” the rows, we may “roll” the columns Even less memory (5 2 entries) Space complexity: (min{N, M}) Drawback Backtracking is difficult That means we can get the number but not the sequence easily. 6

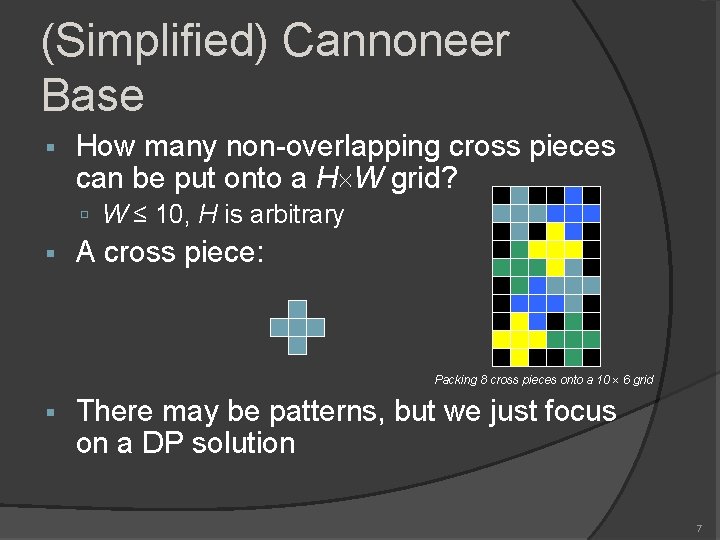
(Simplified) Cannoneer Base How many non-overlapping cross pieces can be put onto a H W grid? W ≤ 10, H is arbitrary A cross piece: Packing 8 cross pieces onto a 10 6 grid There may be patterns, but we just focus on a DP solution 7

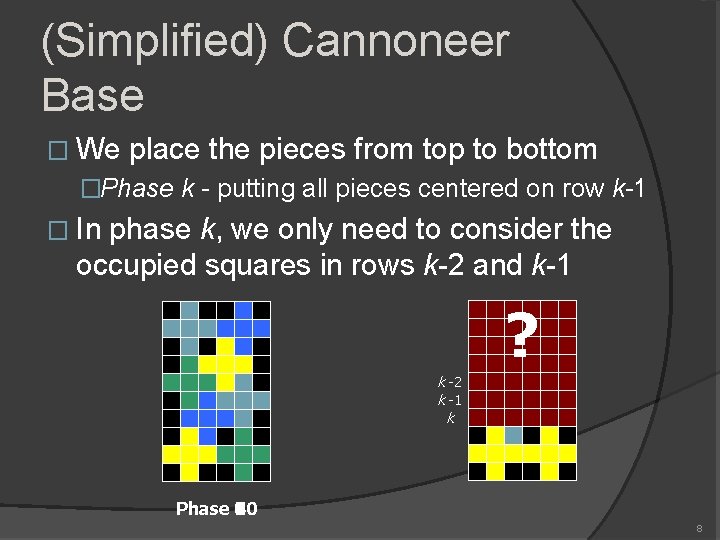
(Simplified) Cannoneer Base � We place the pieces from top to bottom �Phase k - putting all pieces centered on row k-1 � In phase k, we only need to consider the occupied squares in rows k-2 and k-1 ? k -2 k -1 k Phase 10 3 4 5 6 7 8 9 8

(Simplified) Cannoneer Base � The optimal value function C is defined by: �C(k, S) = the max number of pieces after phase k, with rows k-1 and k giving the shape S � How to represent a shape? �In a shape, each column can be �Use 2, 1, 0 to represent these 3 cases �A shape is a W-digit base-3 integer �For example, the following shape is encoded as 010121(3) = 97(10) 9

(Simplified) Cannoneer Base � The recurrence relation is easy to construct � Max possible number of states = H 3 W �That’s why W ≤ 10 � Cannoneer Base appeared in NOI 2001 � Bugs Integrated, Inc. in CEOI 2002 requires similar techniques 10

Dynamic Programming on Tree Structures States may be (related to) nodes on a graph Usually directed acyclic graphs Topological order is the obvious order of recurrence evaluation Trees are special graphs A lot of graph DP problems are based on trees Two major types: Rooted tree DP Unrooted tree DP 11

Rooted Tree Dynamic Programming � Base cases at the leaves � Recurrence at a node involves its child nodes only � Solution �Evaluate the recurrence relation from leaves (bottom) to the root (top) �Top-down implementations work well �Time complexity is often (N) where N is the number of nodes 12

Unrooted Tree Dynamic Programming No explicit roots given � Two cases � �The problem can be transformed to a rooted one �It can’t, so we try root every node Case 2 increases the time complexity by a factor of N � Sometimes it is possible to root one node in O(N) time and each subsequent node in O(1) � �overall O(N) time 13

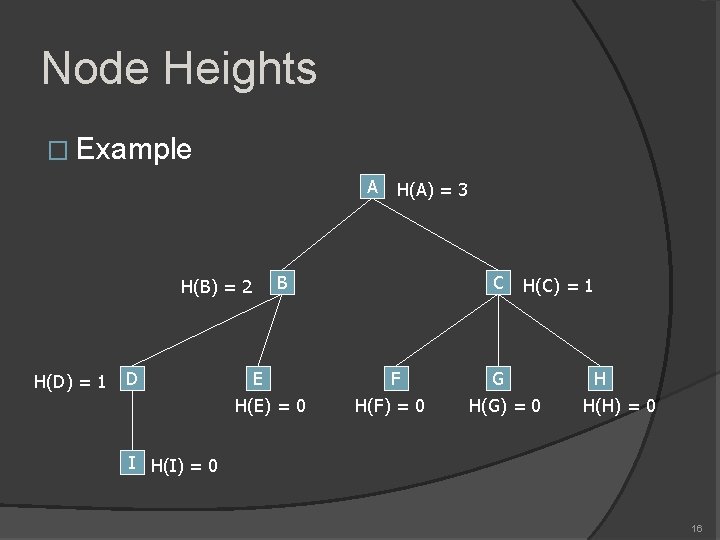
Node Heights � Given a rooted tree T � The height of a node v in T is the maximum distance between v and a descendant of v � For example, all leaves have height = 0 � Find the heights of all nodes in T � Notations �C(v) = the set of children of v �p(v) = the parent of v 14

Node Heights � Optimal value function �H(v) = height of node v � Base conditions �H(u) = 0 for all leaves u � Recurrence �H(v) = max { H(x) | x C(v) } + 1 � Order of evaluation �All children must be evaluated before self �Post-order 15

Node Heights � Example A H(B) = 2 H(D) = 1 D H(A) = 3 B E H(E) = 0 C F H(F) = 0 H(C) = 1 G H(G) = 0 H H(H) = 0 I H(I) = 0 16

Node Heights Time complexity analysis Naively There are N nodes A node may have up to N-1 children Overall time complexity = O(N 2) A better bound The H-value of a v is at most used by one other node – p(v) The total number of H-values inside the “max {}”s = N-1 Overall time complexity = (N) 17

Treasure Hunt �N treasures are hidden at the N nodes of a tree (unrooted) � The treasure at node u has value v(u) � You may not take away two treasures joined by an edge, otherwise missiles will fly to you � Find the maximum value you can take away 18

Treasure Hunt � Let’s see if the problem can be transformed to a rooted one � We arbitrarily root a node, say r � How to formulate? 19

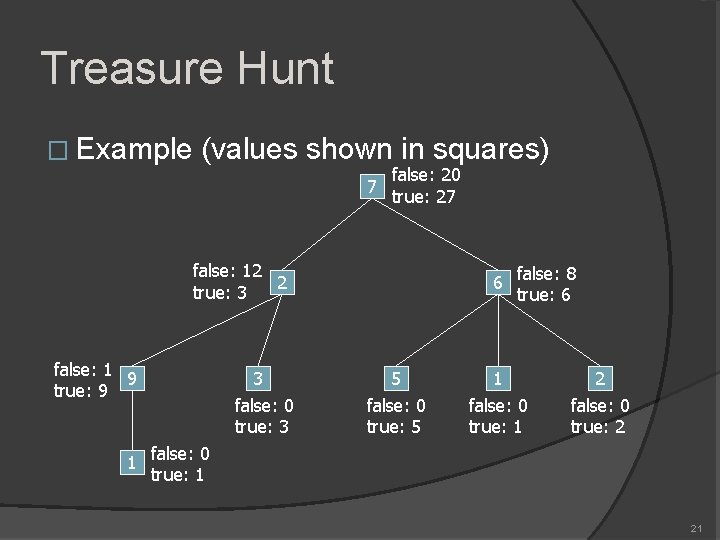
Treasure Hunt Optimal value function Z(u, b) = max value for the subtree rooted at u and it is b that the treasure at u is taken away b = true or false Base conditions Z(x, false) = 0 and Z(x, true) = v(x) for all leaves x Recurrence Z(u, true) = Z(c, false) + v(u) C(u) Z(u, false) = cmax { Z(c, false), Z(c, true) } Answer = maxc {C(u) Z(r, false), Z(r, true) } 20

Treasure Hunt � Example (values shown in squares) 7 false: 20 true: 27 false: 12 2 true: 3 false: 1 9 true: 9 1 3 false: 0 true: 3 6 5 false: 0 true: 5 false: 8 true: 6 1 false: 0 true: 1 21

Treasure Hunt � Our formulation does not exploit the properties of a tree root � Moreover the correctness of our formulation can be proven by optimal substructure � Thus the unrooted-to-rooted transformation is correct � Time complexity: (N) 22

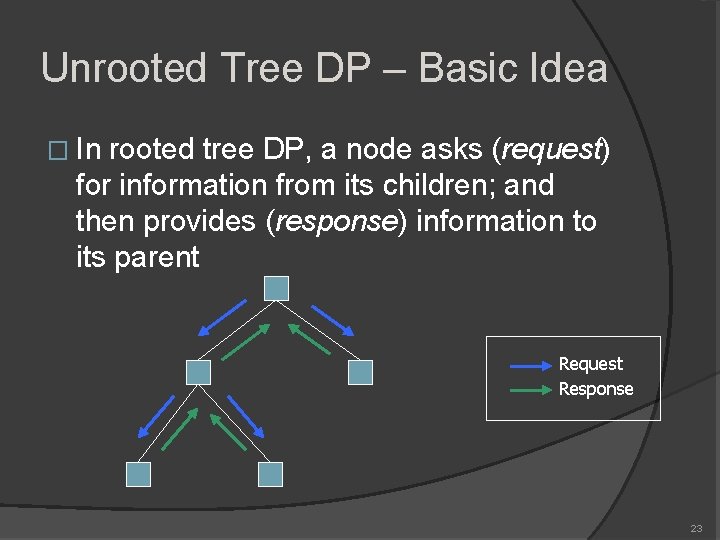
Unrooted Tree DP – Basic Idea � In rooted tree DP, a node asks (request) for information from its children; and then provides (response) information to its parent Request Response 23

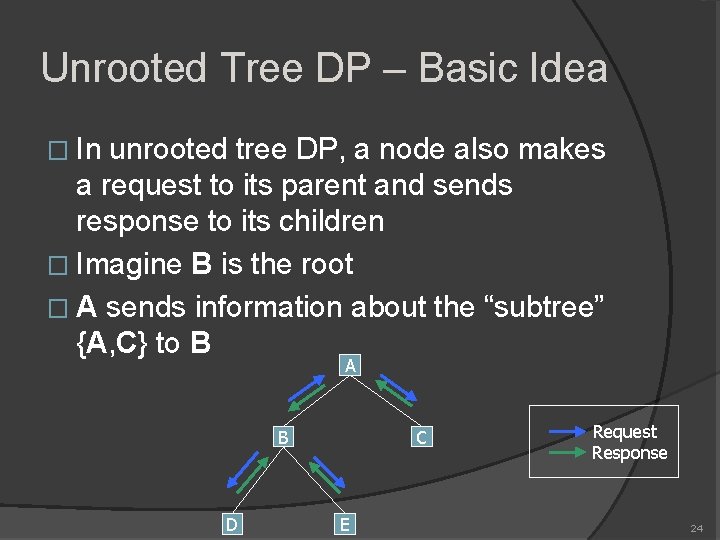
Unrooted Tree DP – Basic Idea � In unrooted tree DP, a node also makes a request to its parent and sends response to its children � Imagine B is the root � A sends information about the “subtree” {A, C} to B A B D C E Request Response 24

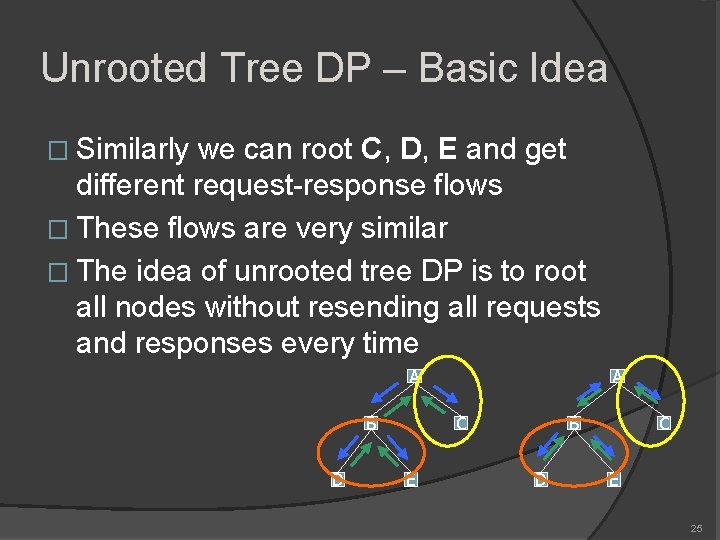
Unrooted Tree DP – Basic Idea � Similarly we can root C, D, E and get different request-response flows � These flows are very similar � The idea of unrooted tree DP is to root all nodes without resending all requests and responses every time A B D A C E B D C E 25

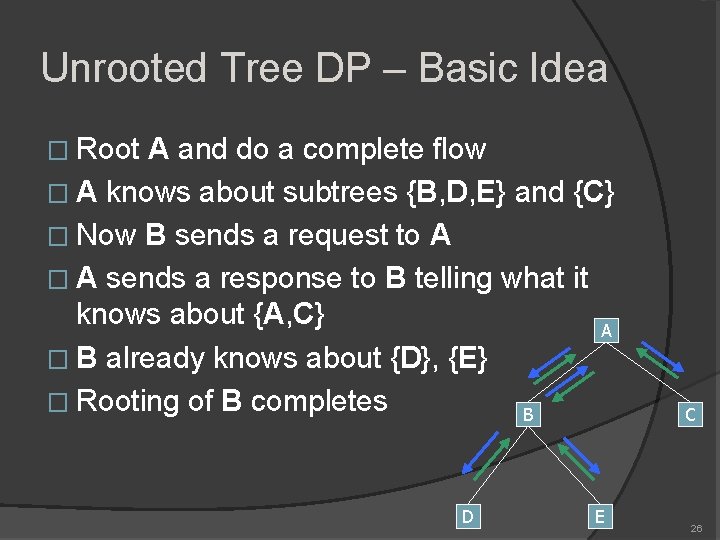
Unrooted Tree DP – Basic Idea � Root A and do a complete flow � A knows about subtrees {B, D, E} and {C} � Now B sends a request to A � A sends a response to B telling what it knows about {A, C} A � B already knows about {D}, {E} � Rooting of B completes B D E C 26

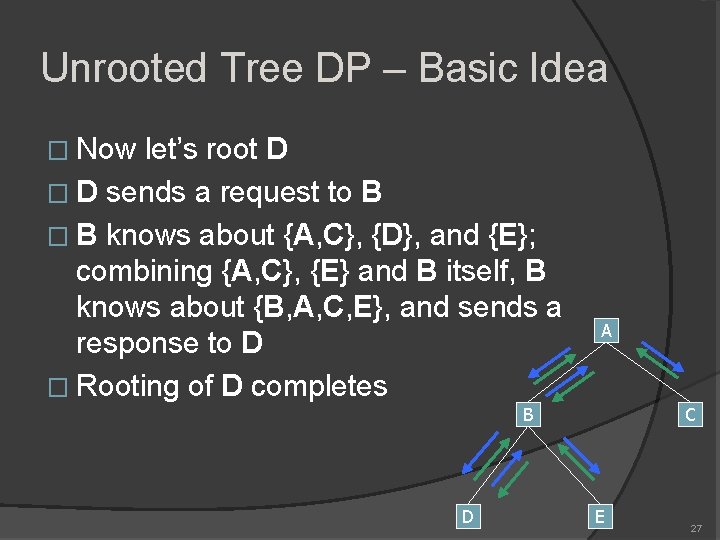
Unrooted Tree DP – Basic Idea � Now let’s root D � D sends a request to B � B knows about {A, C}, {D}, and {E}; combining {A, C}, {E} and B itself, B knows about {B, A, C, E}, and sends a response to D � Rooting of D completes A B D C E 27

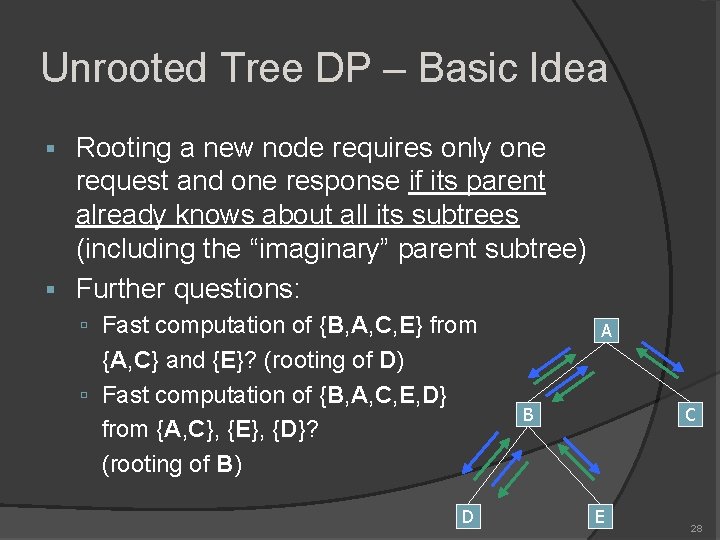
Unrooted Tree DP – Basic Idea Rooting a new node requires only one request and one response if its parent already knows about all its subtrees (including the “imaginary” parent subtree) Further questions: Fast computation of {B, A, C, E} from {A, C} and {E}? (rooting of D) Fast computation of {B, A, C, E, D} from {A, C}, {E}, {D}? (rooting of B) A B D C E 28

Shortest Rooted Tree Given an unrooted tree T, denote its rooted tree with root r by T(r) Find a node v such that T(v) has the minimum height among all T(u), u T The height of a tree = the height of its root Solution Just root every node and find the min height We know how to find a height of a tree Trivially this is (N 2) Now let’s use what we learnt 29

Shortest Rooted Tree � Since parents and children are unclear now, we use slightly different notations � N(v) = the set of neighbors of v � H(v, u) = height of the subtree rooted at v if u is treated as the parent of v � H(v, ) = height of the whole tree if v is root 30

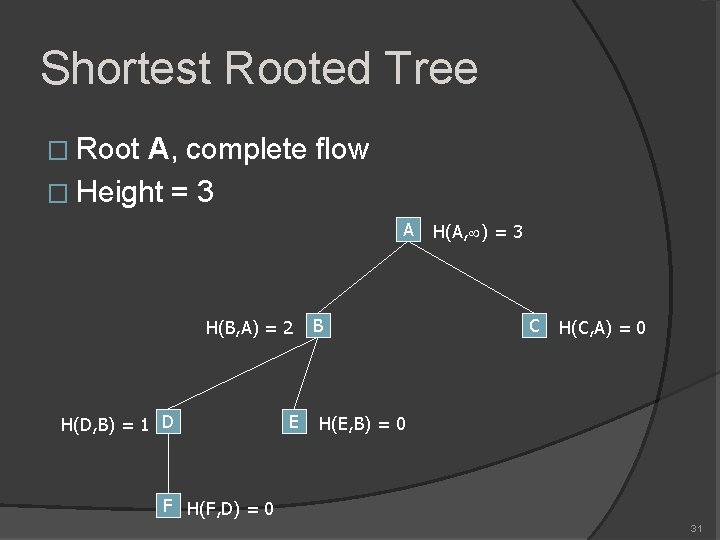
Shortest Rooted Tree � Root A, complete flow � Height = 3 A H(B, A) = 2 H(D, B) = 1 D E B H(A, ) = 3 C H(C, A) = 0 H(E, B) = 0 F H(F, D) = 0 31

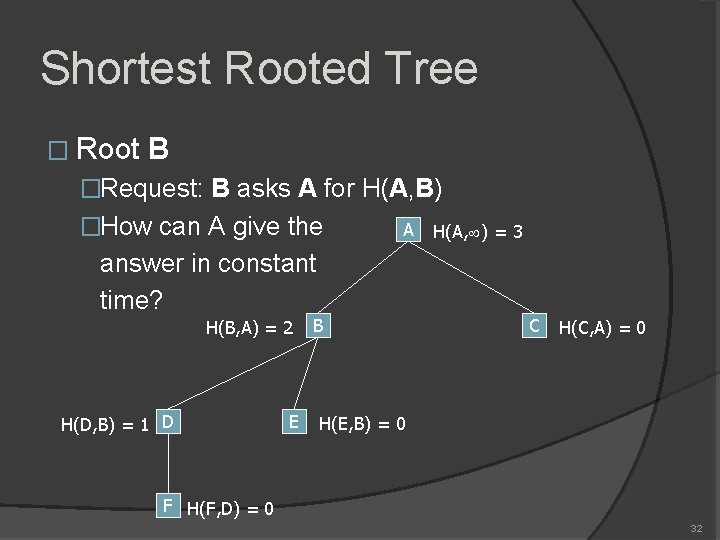
Shortest Rooted Tree � Root B �Request: B asks A for H(A, B) �How can A give the A answer in constant time? H(B, A) = 2 H(D, B) = 1 D E B H(A, ) = 3 C H(C, A) = 0 H(E, B) = 0 F H(F, D) = 0 32

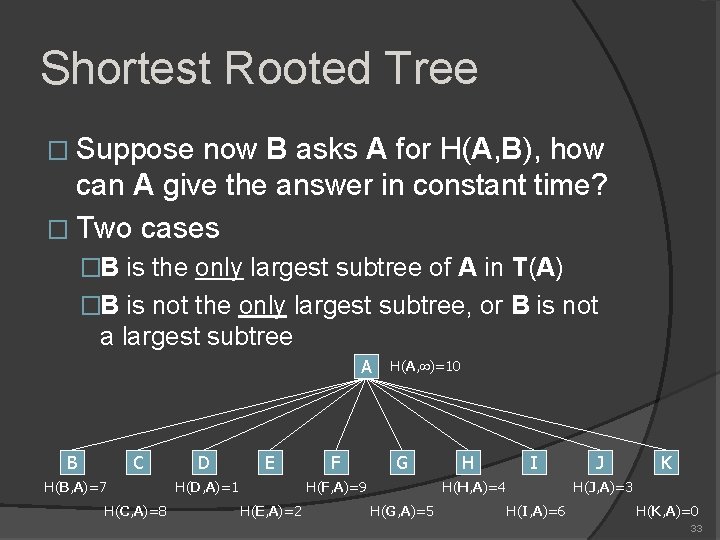
Shortest Rooted Tree � Suppose now B asks A for H(A, B), how can A give the answer in constant time? � Two cases �B is the only largest subtree of A in T(A) �B is not the only largest subtree, or B is not a largest subtree A B C H(B, A)=7 H(C, A)=8 D E H(D, A)=1 F H(A, )=10 G H(F, A)=9 H(E, A)=2 H I H(H, A)=4 H(G, A)=5 J K H(J, A)=3 H(I, A)=6 H(K, A)=0 33

Shortest Rooted Tree � (1) B is the only largest subtree of A in T(A) �H(A, B) < H(A, ) �H(A, B) depends on the second largest subtree �Trick: record the second largest subtree of A � (2) B is not the only largest subtree, or B is not a largest subtree �H(A, B) = H(A, ) 34

Shortest Rooted Tree � To distinguish case (1) from case(2), we need to record the two largest subtrees of A �When? ○ When we evaluate H(A, ) � Back to our example 35

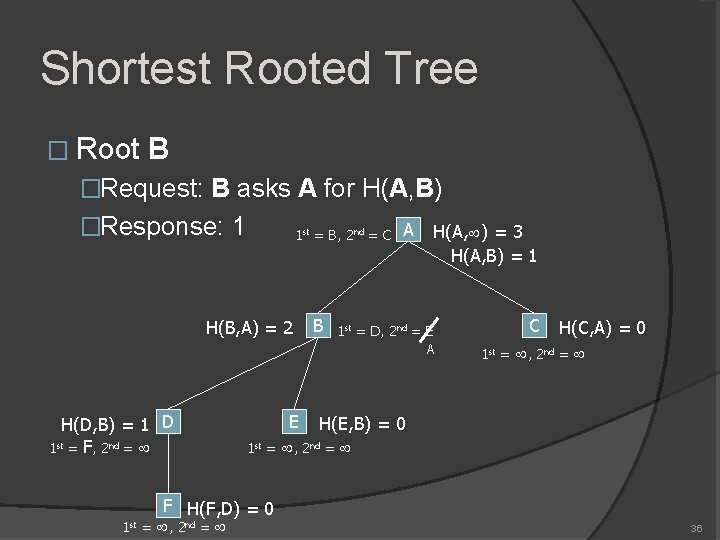
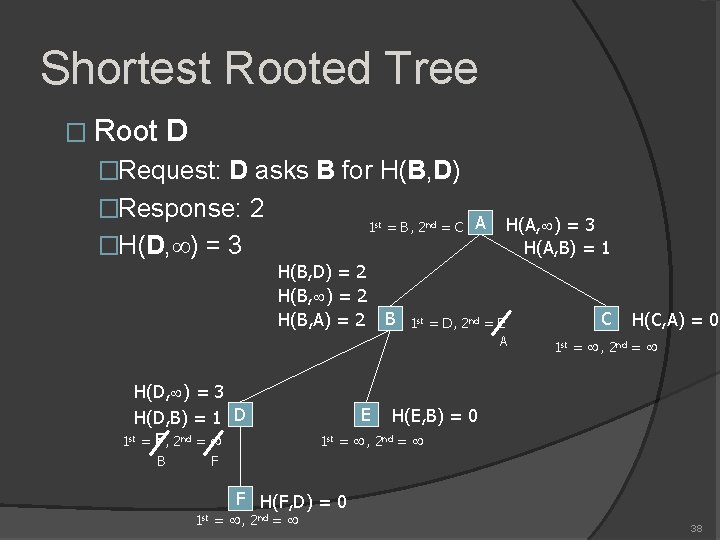
Shortest Rooted Tree � Root B �Request: B asks A for H(A, B) �Response: 1 1 st = B, 2 nd = C H(B, A) = 2 H(D, B) = 1 D 1 st = F, 2 nd = B A H(A, ) = 3 H(A, B) = 1 1 st = D, 2 nd = E A C H(C, A) = 0 1 st = , 2 nd = E H(E, B) = 0 1 st = , 2 nd = F H(F, D) = 0 1 st = , 2 nd = 36

Shortest Rooted Tree � Root B �H(B, ) = 2 can be calculated in constant time 1 st = B, 2 nd = C H(B, ) = 2 H(B, A) = 2 H(D, B) = 1 D 1 st = F, 2 nd = B A H(A, ) = 3 H(A, B) = 1 1 st = D, 2 nd = E A C H(C, A) = 0 1 st = , 2 nd = E H(E, B) = 0 1 st = , 2 nd = F H(F, D) = 0 1 st = , 2 nd = 37

Shortest Rooted Tree � Root D �Request: D asks B for H(B, D) �Response: 2 1 st = B, 2 nd = C �H(D, ) = 3 H(B, D) = 2 H(B, A) = 2 H(D, ) = 3 H(D, B) = 1 D 1 st = F, 2 nd = B B A H(A, ) = 3 H(A, B) = 1 1 st = D, 2 nd = E A C H(C, A) = 0 1 st = , 2 nd = E H(E, B) = 0 1 st = , 2 nd = F F H(F, D) = 0 1 st = , 2 nd = 38

Shortest Rooted Tree � Root F, E, and C in the same fashion � In general, root the nodes in preorder � Time complexity analysis �Root A – (N) �Root each subsequent nodes – O(1) �Overall - (N) � The O(1) is crucial for the linearity of our algorithm �If rooting of a new node cannot be done fast, unrooted tree DP may not improve running time 39

Two-person Games � Often appear in competitions as interactive tasks �Playing against the judge � Most of them can be solved by the Minimax method 40

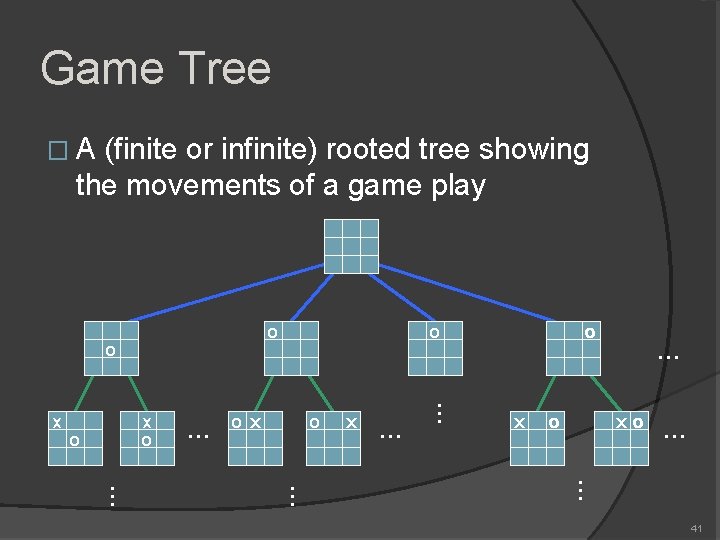
Game Tree �A (finite or infinite) rooted tree showing the movements of a game play o o x o o … o x … … x o o x o … xo … … 41

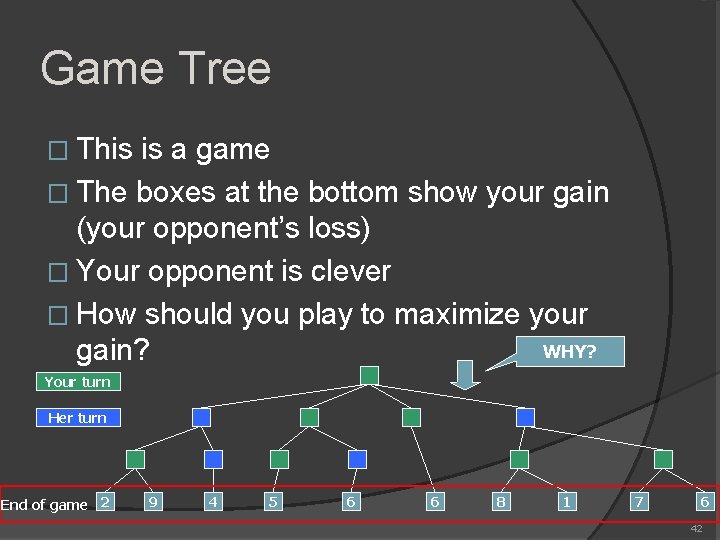
Game Tree � This is a game � The boxes at the bottom show your gain (your opponent’s loss) � Your opponent is clever � How should you play to maximize your WHY? gain? Your turn Her turn End of game 2 9 4 5 6 6 8 1 7 6 42

Minimax � You assume that your opponent always try to minimize her loss (minimize your gain) � So your opponent always takes the move that minimize your gain � Of course, you always take the move that maximize your gain 7 Your turn Her turn 4 9 2 6 4 9 4 5 5 6 7 6 6 8 7 1 7 6 43

Minimax � Efficient? �Only if the tree is small � In fact the game tree may in fact be an expanded version of a directed acyclic graph � Overlapping subproblems memo(r)ization A A B C D B 2 D 1 D 2 2 1 2 1 44

Past Problems IOI NOI 2001 Ioiwari (game), Score (game), Twofive (ugly) 2005 Rivers(tree) 2001 炮兵陣地(ugly), 2002 貪吃的九頭龍 (tree), 2003 逃學的小孩 (tree), 2005 聰聰與可可 IOI/NOITFT CEOI Balkan OI Baltic OI On HKOI Judge 2004 A Bomb Too Far (tree) 2002 Bugs (ugly), 2003 Pearl (game) 2003 Tribe (tree) 2003 Gems (tree) 1074 Christmas Tree 45