Trees Featuring Minimum Spanning Trees HKOI Training 2005

Trees Featuring Minimum Spanning Trees HKOI Training 2005 Advanced Group Presented by Liu Chi Man (cx)

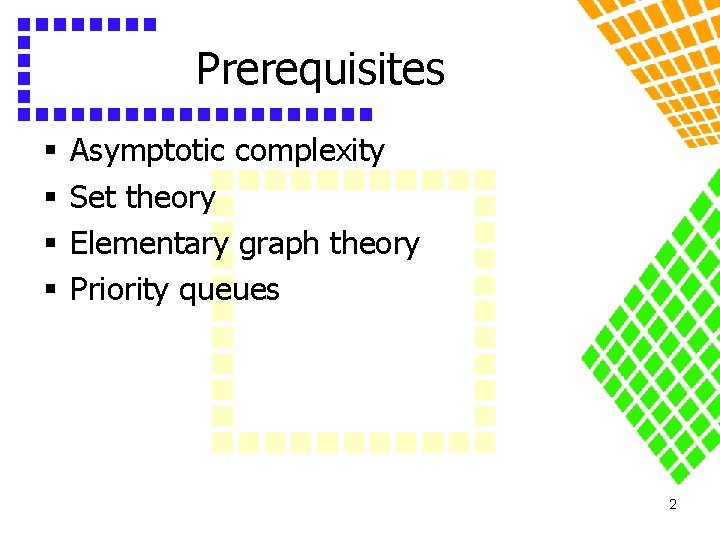
Prerequisites § § Asymptotic complexity Set theory Elementary graph theory Priority queues 2

Assumptions § In the coming slides, we only talk about simple graphs § Extensions to multigraphs and pseudographs should be straightforward if you understand the materials well 3

Notations § A graph G = (V, E) § V is the set of vertices § E is the set of edges § |V| is the number of vertices in V § Sometimes we use V for convenience § |E| is the number of edges in E § Sometimes we use E for convenience 4

Uh… a long way to go § § What is a Tree? Disjoint Sets Minimum Spanning Trees Various Tree Topics 5

What is a Tree? A tree in Pokfulam, Hong Kong. (Photographer: cx) 6

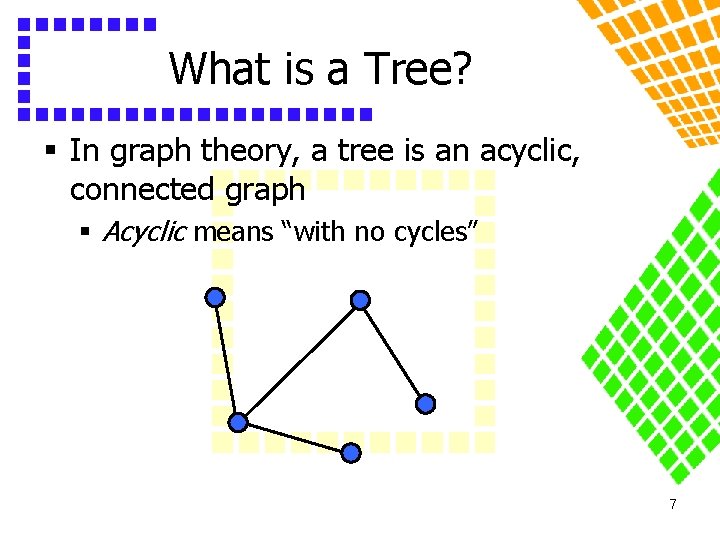
What is a Tree? § In graph theory, a tree is an acyclic, connected graph § Acyclic means “with no cycles” 7

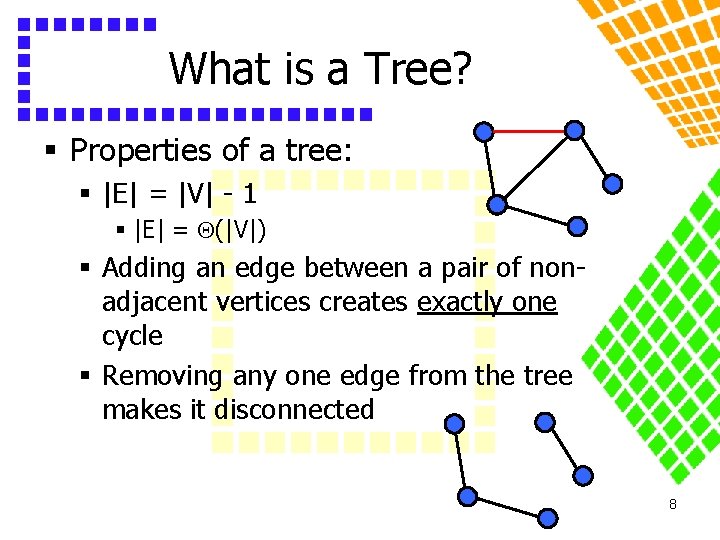
What is a Tree? § Properties of a tree: § |E| = |V| - 1 § |E| = (|V|) § Adding an edge between a pair of nonadjacent vertices creates exactly one cycle § Removing any one edge from the tree makes it disconnected 8

What is a Tree? § The following four conditions are equivalent: § § G is connected and acyclic G is connected and |E| = |V| - 1 G is acyclic and |E| = |V| - 1 Between any pair of vertices in G, there exists a unique path § G is a tree if at least one of the above conditions is satisfied 9

Other Properties of Trees § A tree is bipartite § A tree with at least two vertices has at least two leaves (vertices of degree 1) § A tree is planar 10

Zz. ZZzzz… bored to death? § § What is a Tree? Disjoint Sets Minimum Spanning Trees Various Tree Topics 11

The Union-Find Problem § Initially there are N objects, each in its own singleton set § Let’s label the objects by 1, 2, …, N § So the sets are {1}, {2}, …, {N} § There are two kinds of operations: § Merge two sets (Union) § Find the set to which an object belongs § Let there be a sequence of M operations 12

The Union-Find Problem § § § § An example, with N = 4, M = 5 Initial: {1}, {2}, {3}, {4} Union {1}, {3} {1, 3}, {2}, {4} Find 3. Answer: {1, 3} Union {4}, {1, 3} {1, 3, 4}, {2} Find 2. Answer: {2} Find 1. Answer {1, 3, 4} 13

Disjoint Sets § We usually use disjoint-set data structures to solve the union-find problem § A disjoint set is simply a data structure that supports the Union and Find operations § How should a set be named? § Each set has its own representative element 14

Disjoint Sets § Implementation: Naïve arrays § Set[x] stores the representative of the set containing x, for 1 ≤ x ≤ N § <per Union, per Find>: <O(N), O(1)> § Slight modifications give <O(U), O(1)> § U is the size of the union § Worst case is O(MN) for all M operations 15

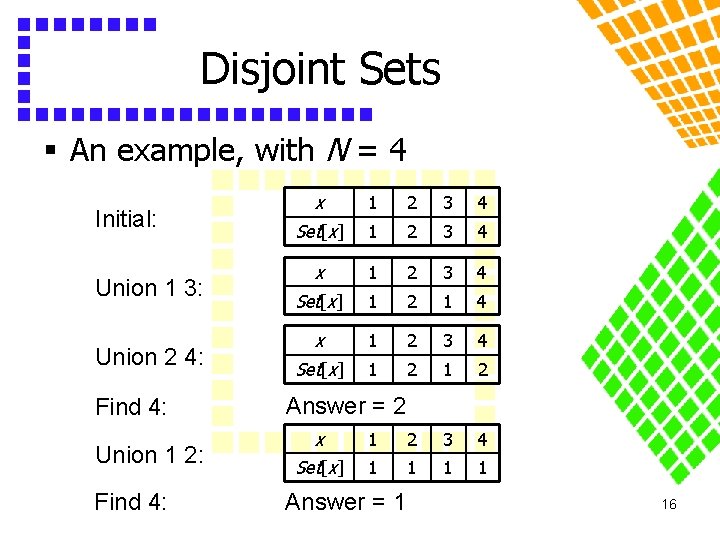
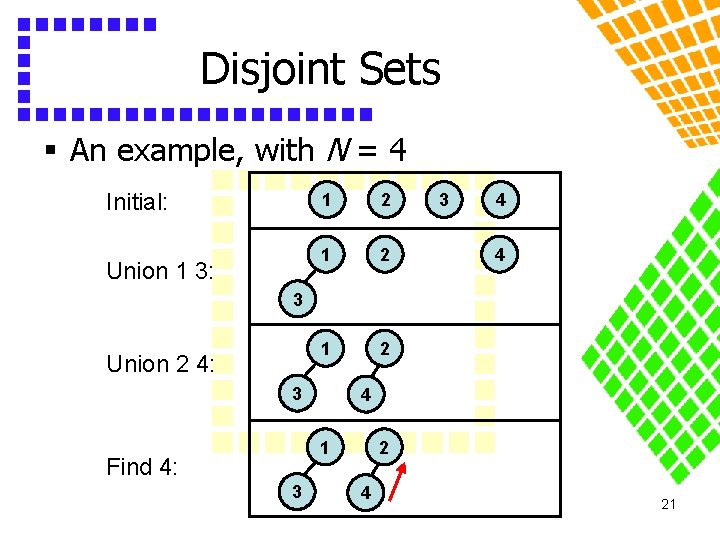
Disjoint Sets § An example, with N = 4 Initial: Union 1 3: Union 2 4: Find 4: Union 1 2: Find 4: x 1 2 3 4 Set[x] 1 2 3 4 x 1 2 3 4 Set[x] 1 2 1 2 Answer = 2 x 1 2 3 4 Set[x] 1 1 Answer = 1 16

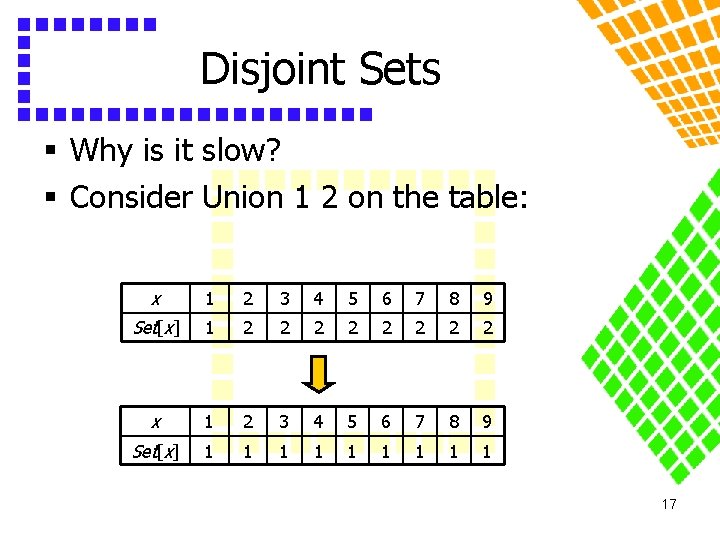
Disjoint Sets § Why is it slow? § Consider Union 1 2 on the table: x 1 2 3 4 5 6 7 8 9 Set[x] 1 2 2 2 2 x 1 2 3 4 5 6 7 8 9 Set[x] 1 1 1 1 17

Disjoint Sets § Idea for improvement: § When doing a Union, always update the set of smaller size § The overall running time can be shown to be O(M lg. N) 18

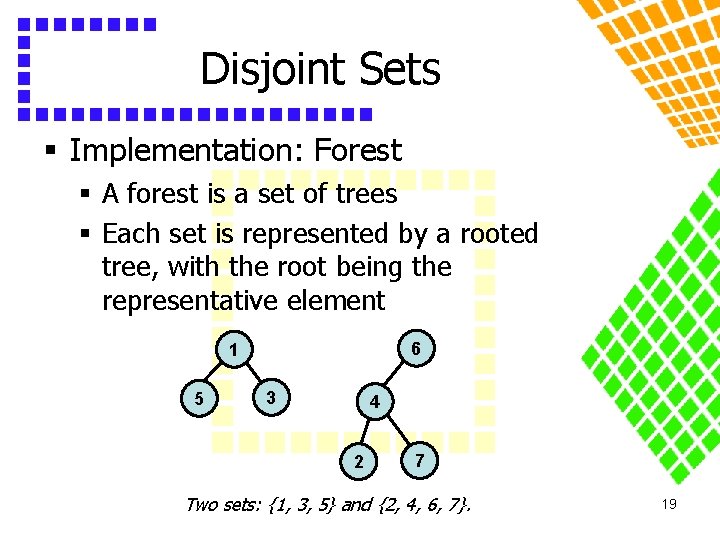
Disjoint Sets § Implementation: Forest § A forest is a set of trees § Each set is represented by a rooted tree, with the root being the representative element 6 1 5 3 4 2 7 Two sets: {1, 3, 5} and {2, 4, 6, 7}. 19

Disjoint Sets § Ideas § Find § Traverses from the vertex up to the root § Union § Merges two trees in the forest § That is, the root of one tree becomes a child of the other tree 20

Disjoint Sets § An example, with N = 4 Initial: Union 1 3: 1 2 1 2 3 4 4 3 Union 2 4: 3 4 1 Find 4: 3 2 4 21

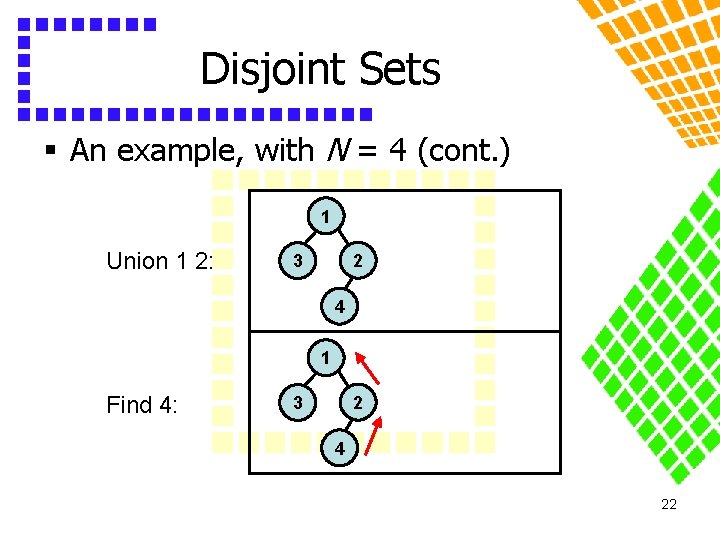
Disjoint Sets § An example, with N = 4 (cont. ) 1 Union 1 2: 2 3 4 1 Find 4: 2 3 4 22

Disjoint Sets § How to represent the trees? § Leftmost-Child-Right-Sibling (LCRS)? § Too complex! § We just need to traverse from bottom to top – parent-finding should be supported § An array Parent[] is enough § Parent[x] stores the parent vertex of x is not the root of a tree § Parent[x] stores x if x is the root of a tree 23

Disjoint Sets § The worst case is still O(MN ) overall § To improve the worst case time complexity, we employ two techniques § Union-by-rank § Path compression 24

Disjoint Sets § Union-by-rank § Recall that in our previous naïve array implementation, the worst case time bound can be improved by always updating the smaller set in a Union § Here, we make the “smaller” tree a subtree of the “larger” tree § To keep the resulting tree “small” § To compare the “sizes” of trees, we assign a rank to every tree in the forest 25

Disjoint Sets § Union-by-rank (cont. ) § The rank of the tree is the height of the tree when it is created § A tree is created either at the beginning, or after a Union § That means we need to keep track of the trees’ ranks during the Unions 26

Disjoint Sets § Path compression § See also the solution for Symbolic Links (HKOI 2005 Senior Final) § When we carry out a Find, we traverse from a vertex to the root § Why don’t we move the vertices closer to the root at the same time? § Closer to the root means shorter query time 27

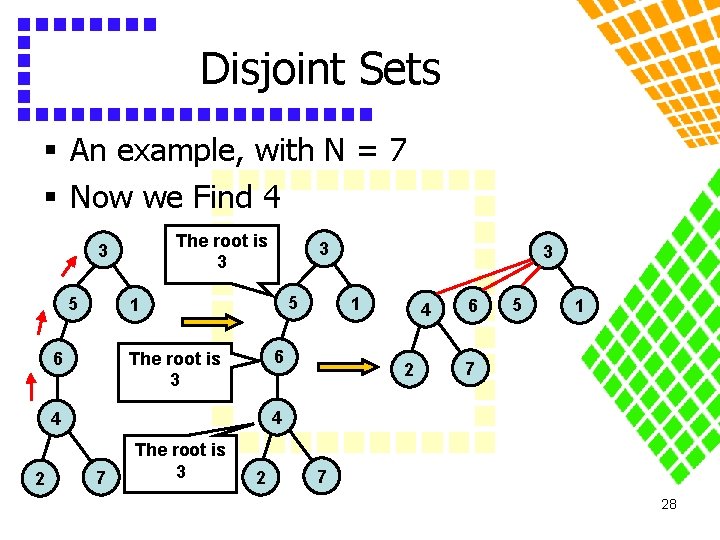
Disjoint Sets § An example, with N = 7 § Now we Find 4 The root is 3 3 5 5 1 6 3 1 6 The root is 3 4 2 6 5 1 7 4 4 2 3 7 The root is 3 2 7 28

Disjoint Sets § We ignore the effect of path compression on tree ranks § Union-by-rank alone gives a running time of O(M lg. N) § Together with path compression, the improved running time is O(M (N)) § is the inverse of the Ackermann's function § (n) is almost constant 29

When can I have my lunch? § § What is a Tree? Disjoint Sets Minimum Spanning Trees Various Tree Topics 30

Minimum Spanning Trees § Given a connected graph G = (V, E), a spanning tree of G is a graph T such that § T is a subgraph of G § T is a tree § T contains every vertex of G § A connected graph must have at least one spanning tree 31

Minimum Spanning Trees § Given a weighted connected graph G, a minimum spanning tree T* of G is a spanning tree of G with minimum total edge weight § Application: Minimizing the total length of wires needed to connect up a collection of computers 32

Minimum Spanning Trees § Two algorithms § Kruskal’s algorithm § Prim’s algorithm 33

Kruskal’s Algorithm § Initially T is an empty set § While T has less than |V|-1 edges Do § Choose an edge with minimum weight such that it does not form a cycle with the edges in T, and add it to T § The edges in T form a MST 34

Kruskal’s Algorithm § Algorithm (Detailed) § T is an empty set § Sort the edges in G by their weights § For (in ascending weight) each edge e Do § If T {e} does not contain a cycle Then § Add e to T § Return T 35

Kruskal’s Algorithm § How to check if a cycle is formed? § Depth-first search (DFS) § Time complexity is O(E 2) § Alternatively, a disjoint set! § The sets are connected components 36

Kruskal’s Algorithm § Algorithm (disjoint-set) § § T is an empty set Create sets {1}, {2}, …, {V} Sort the edges in G by their weights For (in ascending weight) each edge e Do § Let e connect vertices x and y § If Find(x) Find(y) Then § Add e to T, then Union(Find(x), Find(y)) § Return T 37

Kruskal’s Algorithm § The improved time complexity is O(Elg. V) § In fact, the bottleneck is sorting! 38

Prim’s Algorithm § Initially T is a set containing any one vertex in V § While T has less than |V|-1 edges Do § Among those edges connecting a vertex in T and a vertex in V-T, choose one with minimum weight, and add it (with its two end vertices) to T § T is a minimum spanning tree 39

Prim’s Algorithm § Algorithm (Detailed) § § § T Cost[x] for all x V Marked[x] false for all x V Pred[x] for all x V Pick any u V, and set Cost[u] to 0 Repeat |V| times § Let w be a vertex of minimum Cost among all un. Marked vertices § Marked[w] true § T T Pred[x] § For each un. Marked vertex v such that (w, v) E Do § If weight(w, v) < Cost[v] Then § Cost[v] weight(w, v) § Pred[x] { (w, v) } § Return T 40

Prim’s Algorithm § Time complexity: O(V 2) § If a (binary) heap is used to accelerate the Find-Min operations, the time complexity is reduced to O(Elg. V) § O(Vlg. V+E) if a Fibonacci heap is used 41

Minimum Spanning Trees § The fastest known algorithm runs in O(E (V, E)) 42

MST Extensions § Second-best MST § We don’t want the best! § Online MST § See IOI 2003 Path Maintenance § Minimum Bottleneck Spanning Tree § The bottleneck of a spanning tree is the weight of its maximum weight edge § An algorithm that runs in O(V+E) exists 43

MST Extensions (NP-Hard) § Minimum Steiner Tree § No need to connect all vertices, but at least a given subset B V § Degree-bounded MST § Every vertex of the spanning tree must have degree not greater than a given value K 44

Are you with me? § § What is a Tree? Disjoint Sets Minimum Spanning Trees Various Tree Topics 45

Various Tree Topics § Center and diameter § Tree isomorphism § Canonical representation § Prüfer code § Lowest common ancestor (LCA) 46

Supplementary Readings § Advanced: § § Disjoint set forest (Lecture slides) Prim’s algorithm Kruskal’s algorithm Center and diameter § Post-advanced (so-called Beginners): § Lowest common ancestor § Maximum branching 47