Graphs Paths trees and flows Jordi Cortadella and

Graphs: Paths, trees and flows Jordi Cortadella and Jordi Petit Department of Computer Science

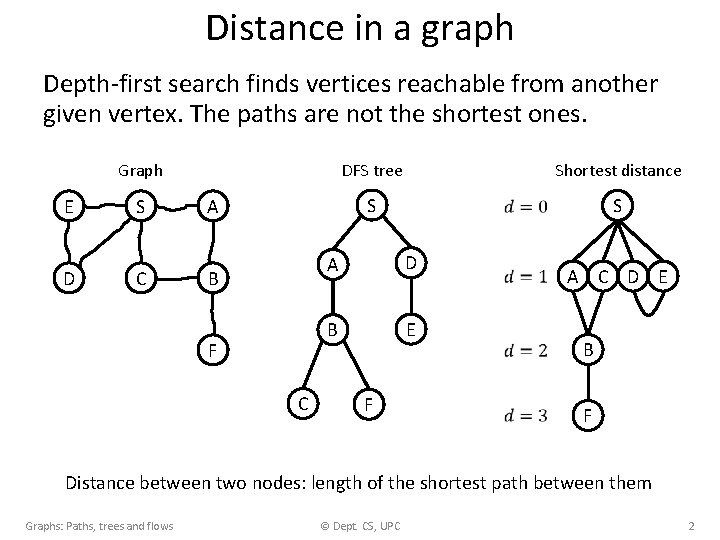
Distance in a graph Depth-first search finds vertices reachable from another given vertex. The paths are not the shortest ones. Graph E D S C DFS tree Shortest distance S A B F C A D B E F S A C D E B F Distance between two nodes: length of the shortest path between them Graphs: Paths, trees and flows © Dept. CS, UPC 2

Breadth-first search Similar to a wave propagation Graphs: Paths, trees and flows © Dept. CS, UPC 3

Breadth-first search Graphs: Paths, trees and flows © Dept. CS, UPC 4

Breadth-first search 6 5 4 3 2 3 4 5 6 5 4 3 2 1 2 3 4 5 4 3 2 1 0 1 2 3 4 5 4 3 2 1 2 3 4 5 6 5 4 3 2 3 4 5 6 Graphs: Paths, trees and flows © Dept. CS, UPC 5

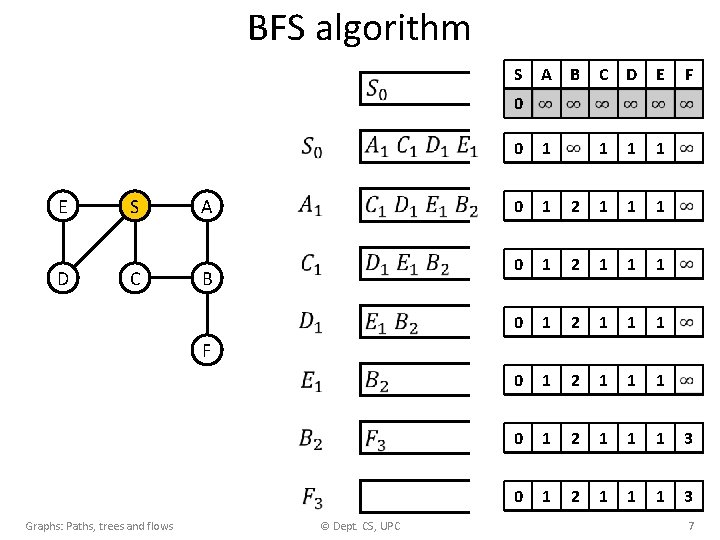
BFS algorithm • Graphs: Paths, trees and flows © Dept. CS, UPC 6

BFS algorithm E D S C A B S A B C D E 1 1 1 F 0 0 1 2 1 1 1 0 1 2 1 1 1 3 F Graphs: Paths, trees and flows © Dept. CS, UPC 7

BFS algorithm Graphs: Paths, trees and flows © Dept. CS, UPC 8

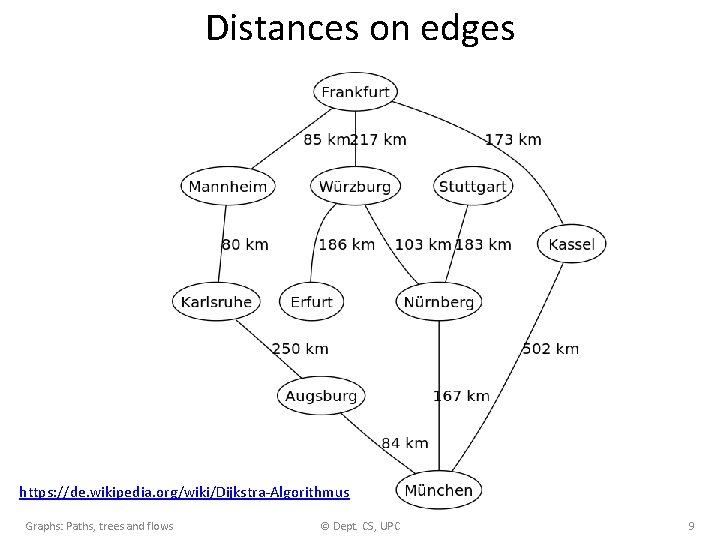
Distances on edges https: //de. wikipedia. org/wiki/Dijkstra-Algorithmus Graphs: Paths, trees and flows © Dept. CS, UPC 9

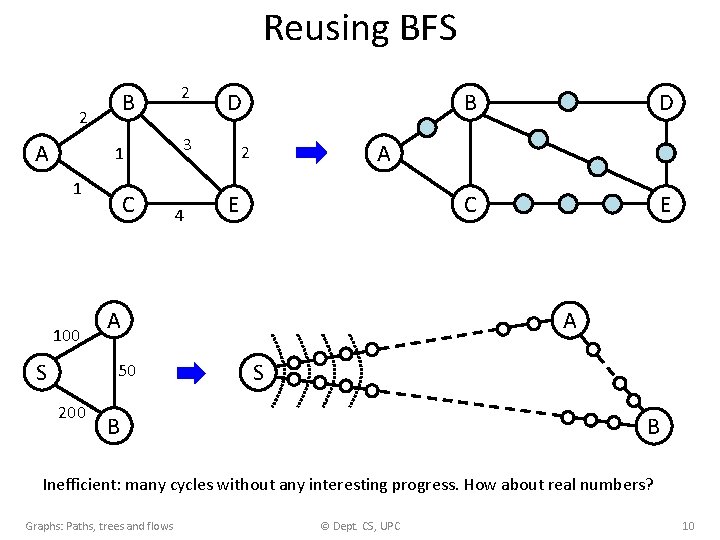
Reusing BFS B 2 A 1 1 100 S C D 3 4 B D C E A 2 E A 50 200 2 A S B B Inefficient: many cycles without any interesting progress. How about real numbers? Graphs: Paths, trees and flows © Dept. CS, UPC 10

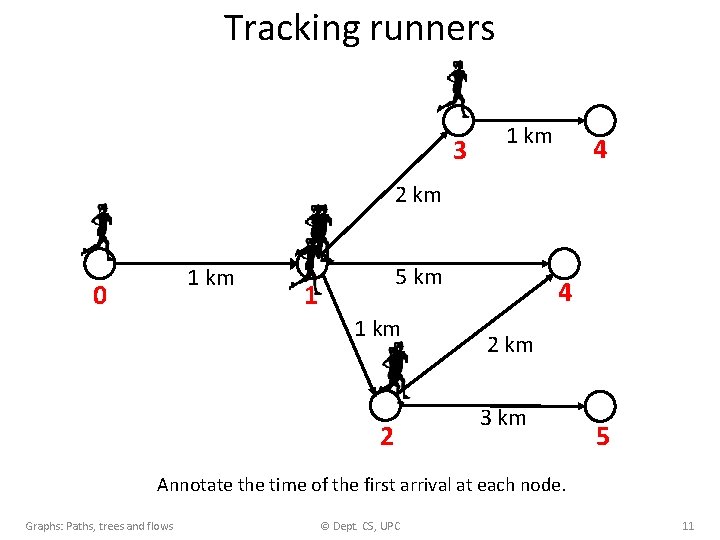
Tracking runners 3 1 km 4 2 km 1 km 0 5 km 1 1 km 2 4 2 km 3 km 5 Annotate the time of the first arrival at each node. Graphs: Paths, trees and flows © Dept. CS, UPC 11

The runners algorithm • Graphs: Paths, trees and flows © Dept. CS, UPC 12

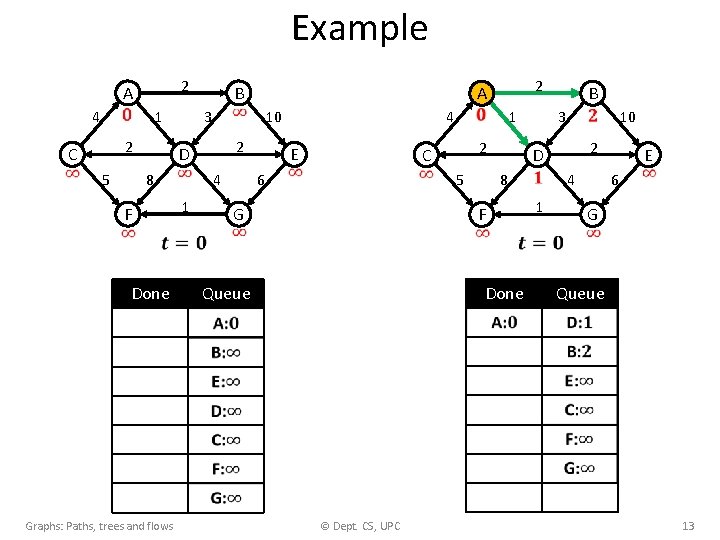
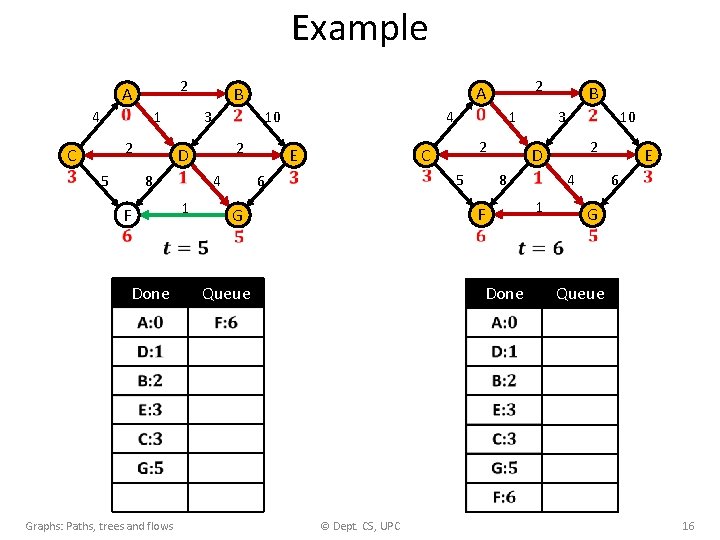
Example 4 2 A 1 2 C 5 D 8 1 F Done Graphs: Paths, trees and flows 3 B 10 4 2 4 6 E G 2 A 1 2 C 5 1 F Done Queue © Dept. CS, UPC 3 D 8 B 10 2 4 6 E G Queue 13

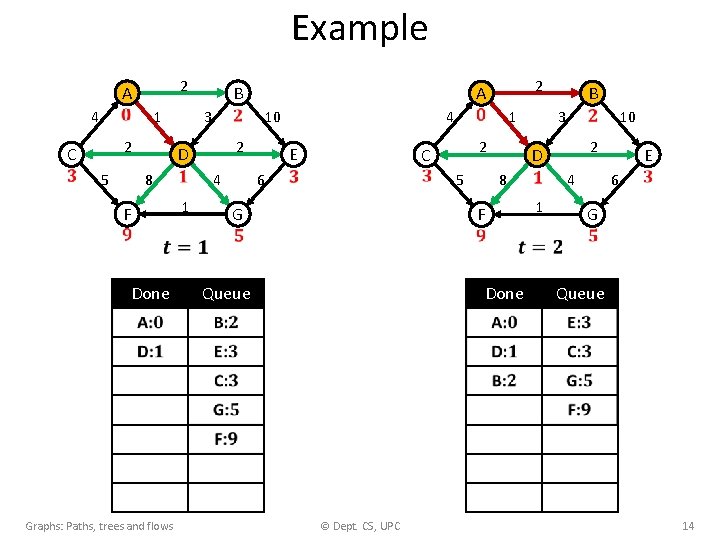
Example 4 C 2 A 1 2 5 3 D 8 1 F Done Graphs: Paths, trees and flows B 10 2 4 6 4 E C G 1 2 5 1 F Done © Dept. CS, UPC B 3 D 8 Queue 2 A 10 2 4 6 E G Queue 14

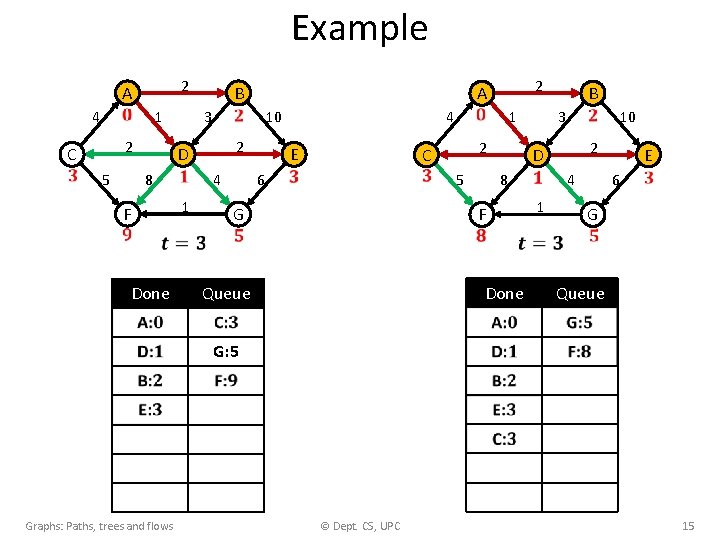
Example 4 C 2 A 1 2 5 3 D 8 1 F Done B 10 2 4 6 4 E C G 2 A 1 2 5 1 F Done Queue 3 D 8 B 10 2 4 6 E G Queue G: 5 Graphs: Paths, trees and flows © Dept. CS, UPC 15

Example 4 C 2 A 1 2 5 3 D 8 1 F Done Graphs: Paths, trees and flows B 2 4 4 10 6 C E G 1 2 5 1 F Done © Dept. CS, UPC B 3 D 8 Queue 2 A 10 2 4 6 E G Queue 16

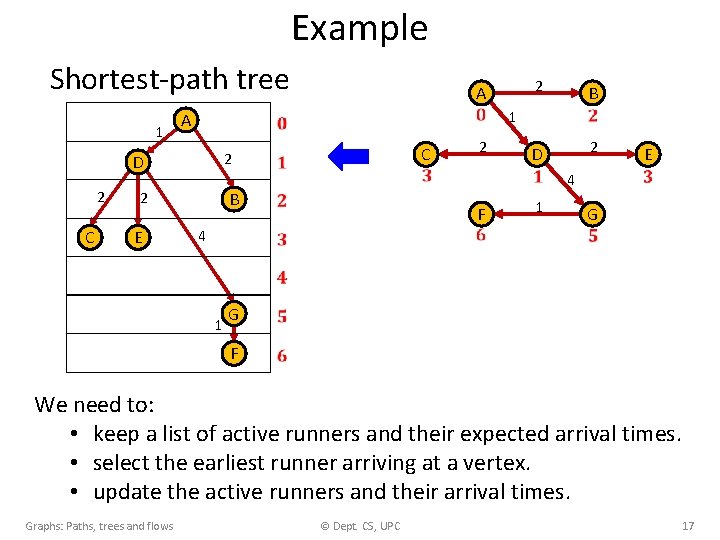
Example Shortest-path tree 1 A 2 D 2 C B 2 E A 4 2 C F 2 B D 2 1 1 4 E G 1 G F We need to: • keep a list of active runners and their expected arrival times. • select the earliest runner arriving at a vertex. • update the active runners and their arrival times. Graphs: Paths, trees and flows © Dept. CS, UPC 17

Dijkstra’s algorithm for shortest paths Graphs: Paths, trees and flows © Dept. CS, UPC 18

Dijkstra’s algorithm: complexity Graphs: Paths, trees and flows © Dept. CS, UPC 19

Dijkstra’s algorithm: complexity Implementation deletemin insert/ decreasekey Dijkstra’s complexity Vector Binary heap Graphs: Paths, trees and flows © Dept. CS, UPC 20

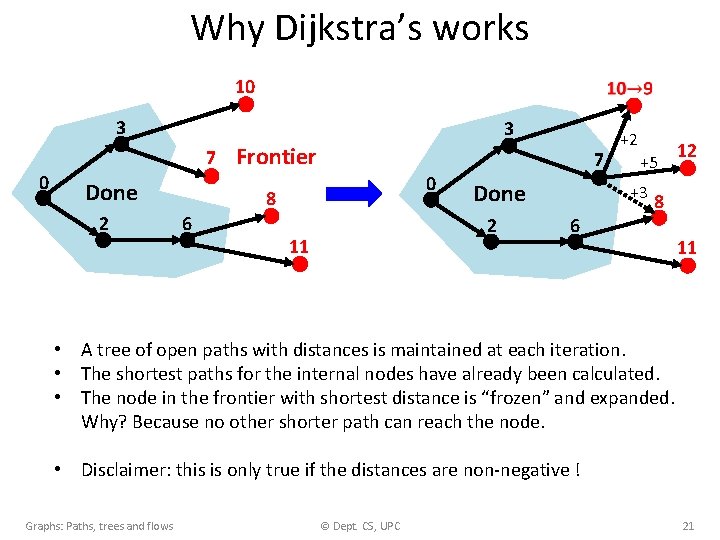
Why Dijkstra’s works 10 3 3 7 0 Done 2 Frontier 0 8 6 7 Done 2 11 +2 +5 +3 6 12 8 11 • A tree of open paths with distances is maintained at each iteration. • The shortest paths for the internal nodes have already been calculated. • The node in the frontier with shortest distance is “frozen” and expanded. Why? Because no other shorter path can reach the node. • Disclaimer: this is only true if the distances are non-negative ! Graphs: Paths, trees and flows © Dept. CS, UPC 21

Graphs with negative edges • 3 A -2 S 4 Graphs: Paths, trees and flows Dijkstra would say that the shortest path S A has length=3. B © Dept. CS, UPC 22

Graphs with negative edges • Graphs: Paths, trees and flows © Dept. CS, UPC 23

Bellman-Ford algorithm Graphs: Paths, trees and flows © Dept. CS, UPC 24

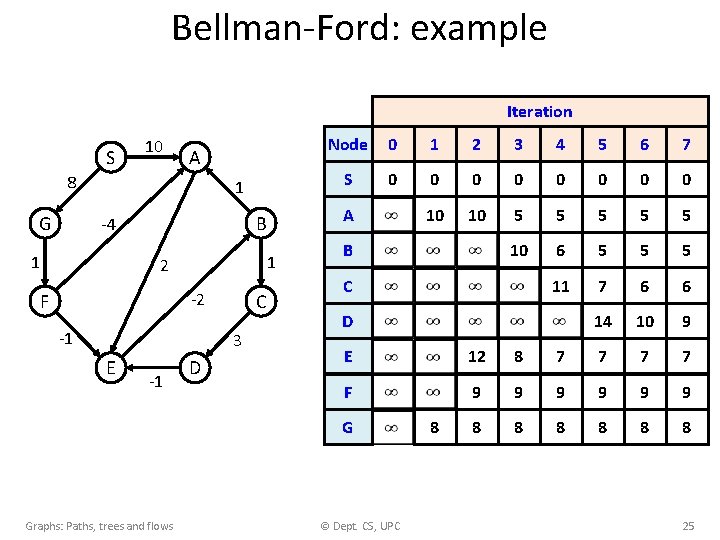
Bellman-Ford: example Iteration S 10 A 8 G 1 B -4 1 1 2 -2 F -1 C 3 E -1 Graphs: Paths, trees and flows D Node 0 1 2 3 4 5 6 7 S 0 0 0 0 10 10 5 5 5 10 6 5 5 5 11 7 6 6 14 10 9 A B C D E 12 8 7 7 F 9 9 9 G 8 8 8 © Dept. CS, UPC 8 25

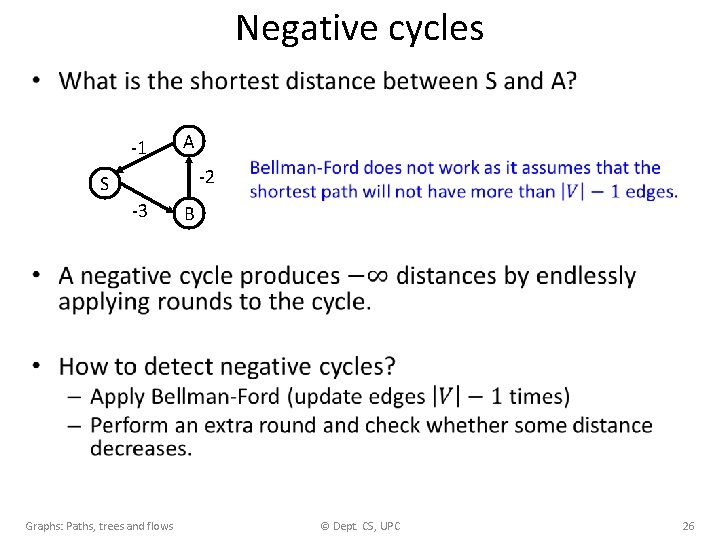
Negative cycles • -1 A -2 S -3 Graphs: Paths, trees and flows B © Dept. CS, UPC 26

Shortest paths in DAGs • Graphs: Paths, trees and flows © Dept. CS, UPC 27

DAG shortest paths algorithm Graphs: Paths, trees and flows © Dept. CS, UPC 28

Shortest paths: summary Single-source shortest paths Graph Non-negative edges Algorithm Dijkstra Negative edges DAG Bellman-Ford Topological sort Complexity Graphs: Paths, trees and flows © Dept. CS, UPC 29

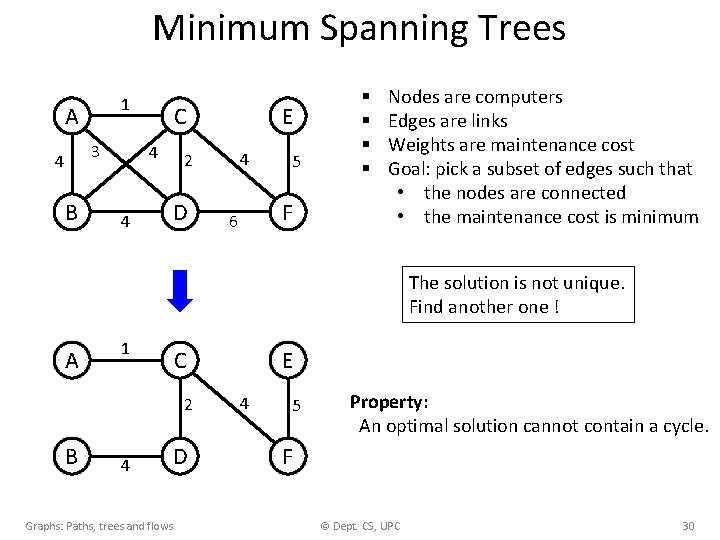
Minimum Spanning Trees 1 A 3 4 B C 4 4 E 4 2 D 5 F 6 § § Nodes are computers Edges are links Weights are maintenance cost Goal: pick a subset of edges such that • the nodes are connected • the maintenance cost is minimum The solution is not unique. Find another one ! A 1 C 2 B 4 D Graphs: Paths, trees and flows E 4 5 Property: An optimal solution cannot contain a cycle. F © Dept. CS, UPC 30

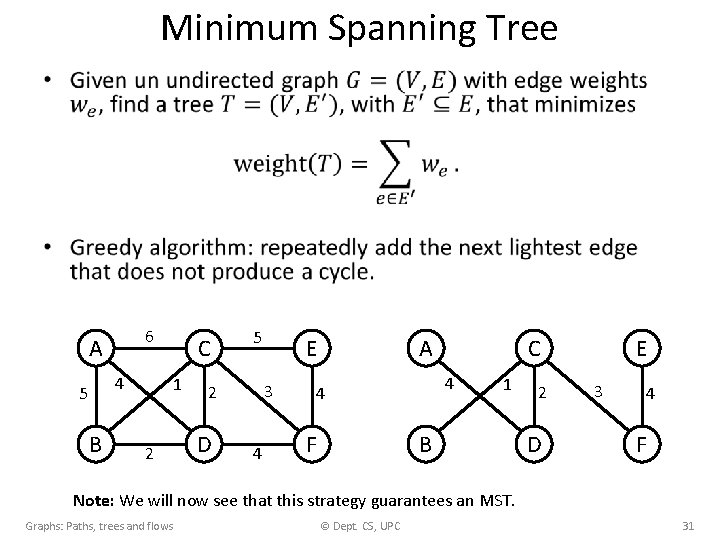
Minimum Spanning Tree • 6 A 4 5 B C 1 2 5 3 2 D E 4 A 4 4 F C 1 B 2 D E 3 4 F Note: We will now see that this strategy guarantees an MST. Graphs: Paths, trees and flows © Dept. CS, UPC 31

Properties of trees • Graphs: Paths, trees and flows © Dept. CS, UPC 32

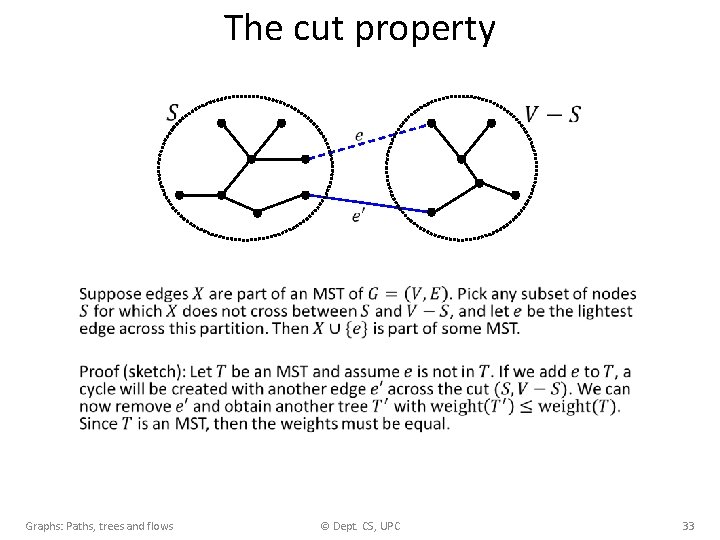
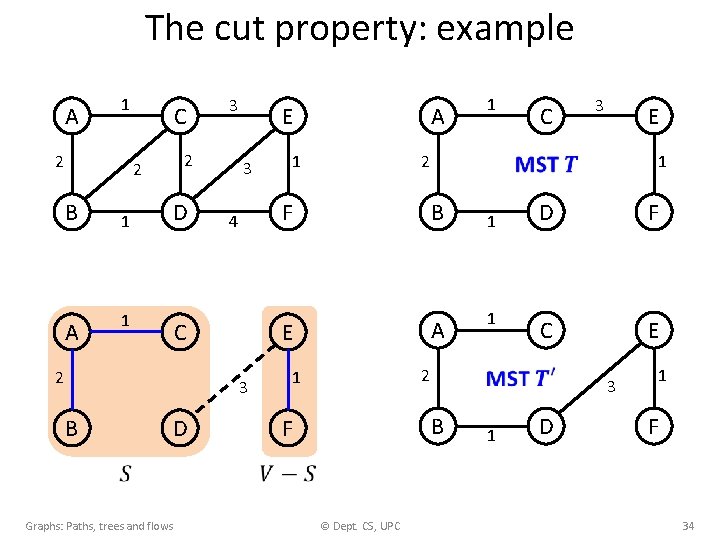
The cut property • Graphs: Paths, trees and flows © Dept. CS, UPC 33

The cut property: example 1 A 2 C 2 2 B 1 D 1 A 3 E 1 3 4 C 2 D Graphs: Paths, trees and flows F B E A E 1 1 1 D F C E 2 B F C 3 2 1 3 B A 1 1 3 D 1 F © Dept. CS, UPC 34

Minimum Spanning Tree Any scheme like this works (because of the properties of trees): Graphs: Paths, trees and flows © Dept. CS, UPC 35

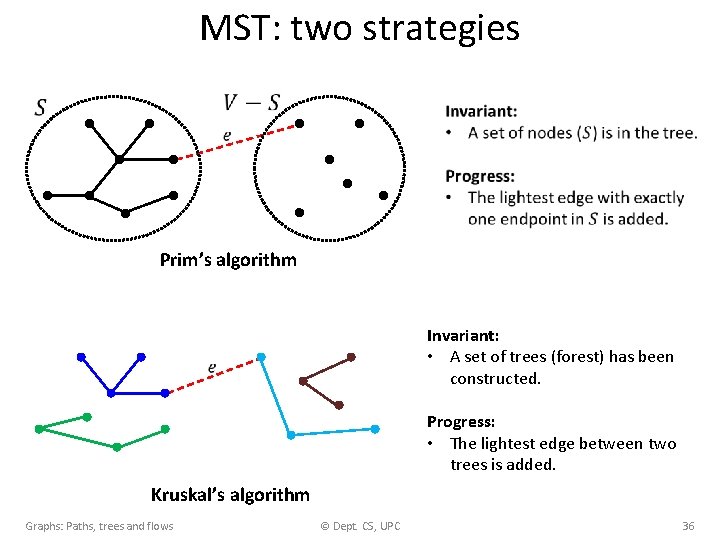
MST: two strategies Prim’s algorithm Invariant: • A set of trees (forest) has been constructed. Progress: • The lightest edge between two trees is added. Kruskal’s algorithm Graphs: Paths, trees and flows © Dept. CS, UPC 36

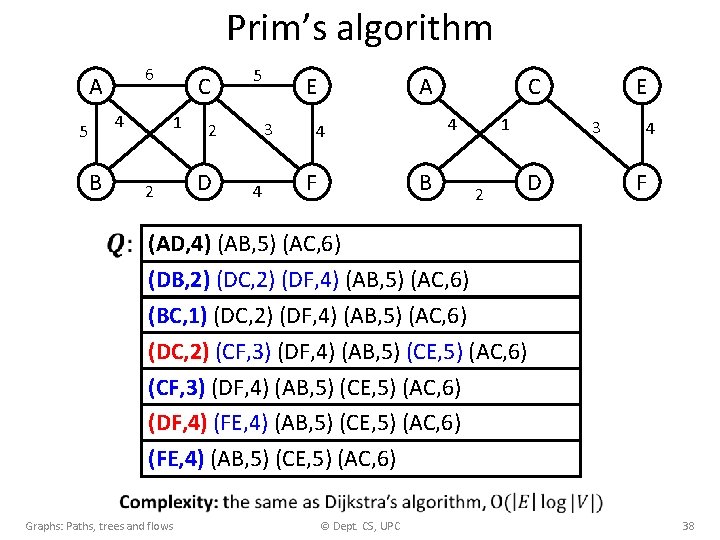
Prim’s algorithm Graphs: Paths, trees and flows © Dept. CS, UPC 37

Prim’s algorithm 6 A 4 5 B 1 2 C 5 3 2 D E 4 A 4 4 F C B 1 2 E 3 D 4 F (AD, 4) (AB, 5) (AC, 6) (DB, 2) (DC, 2) (DF, 4) (AB, 5) (AC, 6) (BC, 1) (DC, 2) (DF, 4) (AB, 5) (AC, 6) (DC, 2) (CF, 3) (DF, 4) (AB, 5) (CE, 5) (AC, 6) (DF, 4) (FE, 4) (AB, 5) (CE, 5) (AC, 6) Graphs: Paths, trees and flows © Dept. CS, UPC 38

Kruskal’s algorithm Informal algorithm: • Sort edges by weight. • Visit edges in ascending order of weight and add them as long as they do not create a cycle. How do we know whether a new edge will create a cycle? Graphs: Paths, trees and flows © Dept. CS, UPC 39

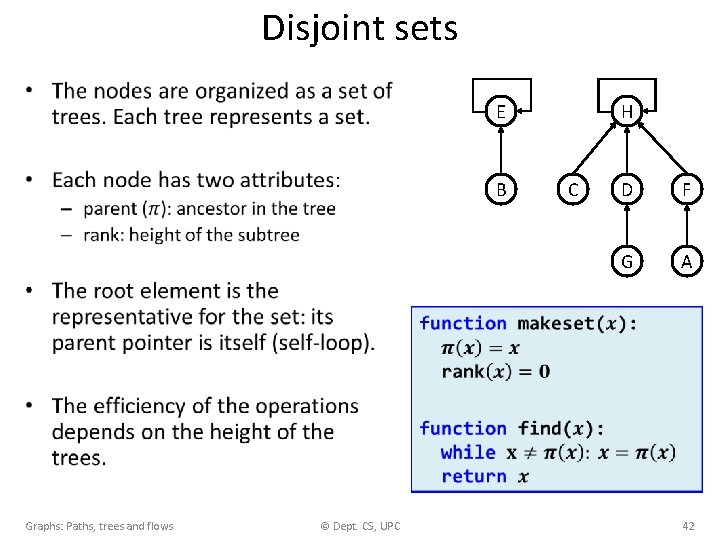
Disjoint sets • Graphs: Paths, trees and flows © Dept. CS, UPC 40

Kruskal’s algorithm Graphs: Paths, trees and flows © Dept. CS, UPC 41

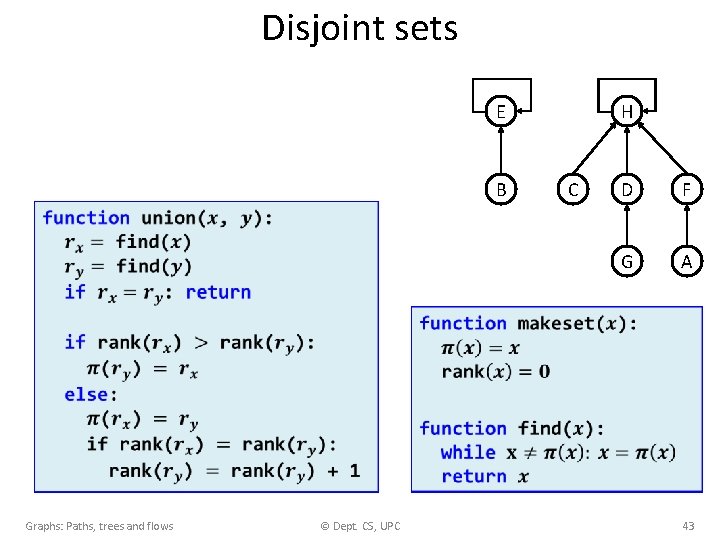
Disjoint sets • E B H C D F G A Graphs: Paths, trees and flows © Dept. CS, UPC 42

Disjoint sets E B C D F G A Graphs: Paths, trees and flows H © Dept. CS, UPC 43

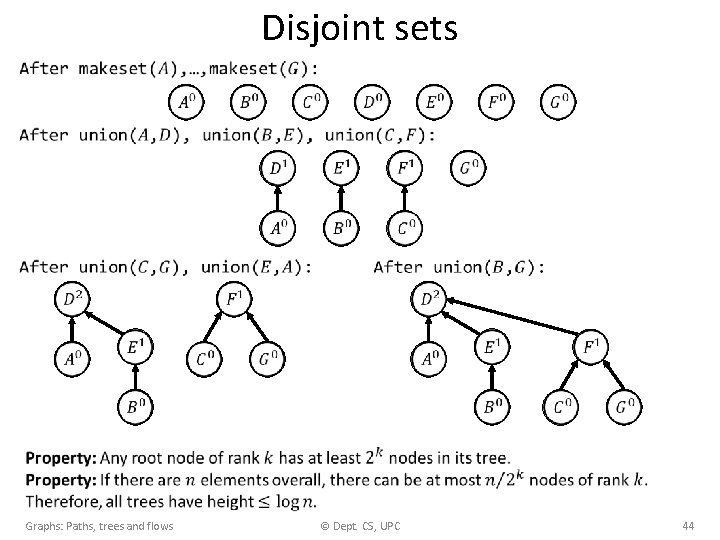
Disjoint sets Graphs: Paths, trees and flows © Dept. CS, UPC 44

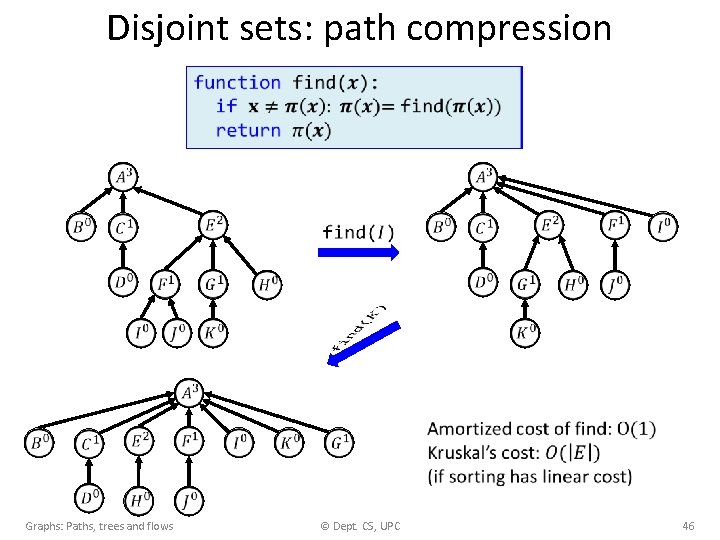
Disjoint sets: path compression • A A B C D E F B C D E A F G B C D E F G G Graphs: Paths, trees and flows © Dept. CS, UPC 45

Disjoint sets: path compression • Graphs: Paths, trees and flows © Dept. CS, UPC 46

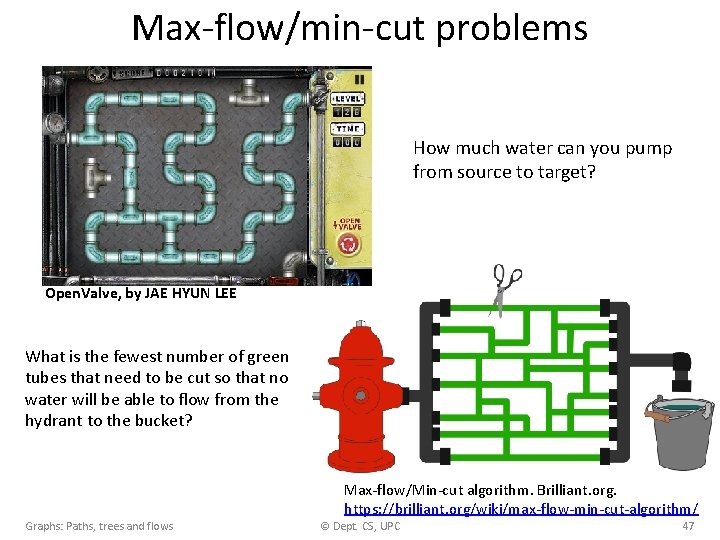
Max-flow/min-cut problems How much water can you pump from source to target? Open. Valve, by JAE HYUN LEE What is the fewest number of green tubes that need to be cut so that no water will be able to flow from the hydrant to the bucket? Max-flow/Min-cut algorithm. Brilliant. org. https: //brilliant. org/wiki/max-flow-min-cut-algorithm/ Graphs: Paths, trees and flows © Dept. CS, UPC 47

Max-flow/min-cut problems: applications • Networks that carry data, water, oil, electricity, cars, etc. – How to maximize usage? – How to minimize cost? – How to maximize reliability? • Multiple application domains: – – – – Computer networks Image processing Computational biology Airline scheduling Data mining Distributed computing … Graphs: Paths, trees and flows © Dept. CS, UPC 48

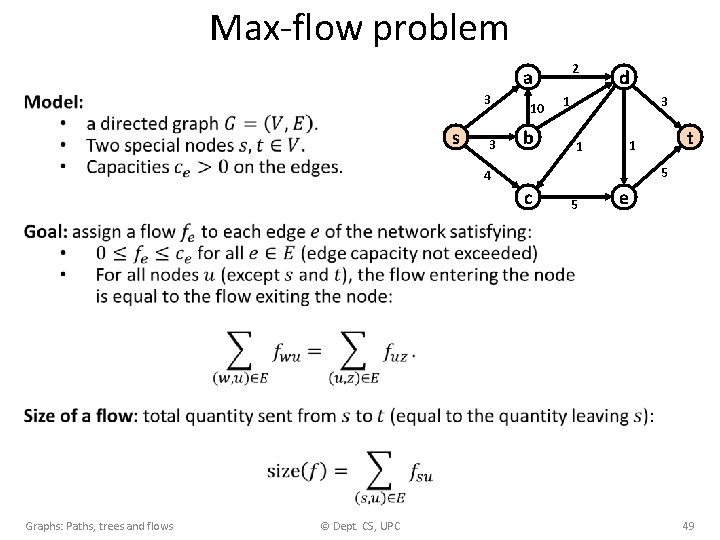
Max-flow problem 2 a 3 s 3 10 b d 3 1 1 5 4 c Graphs: Paths, trees and flows © Dept. CS, UPC t 1 5 e 49

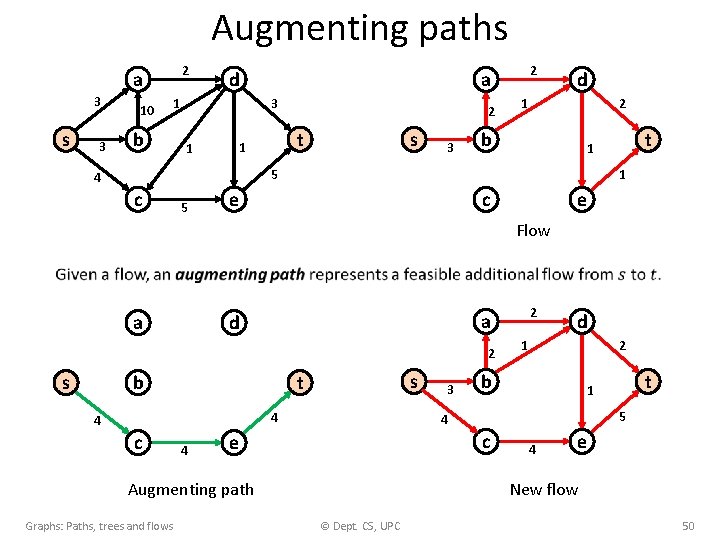
Augmenting paths 2 a 3 s 3 10 b d 3 1 1 2 a 2 t 1 s 3 d 2 1 b 5 4 c 5 t 1 1 e c e Flow a 2 s b s t 4 4 c 4 3 d 2 1 b 5 c e t 1 4 Augmenting path Graphs: Paths, trees and flows 2 a d 4 e New flow © Dept. CS, UPC 50

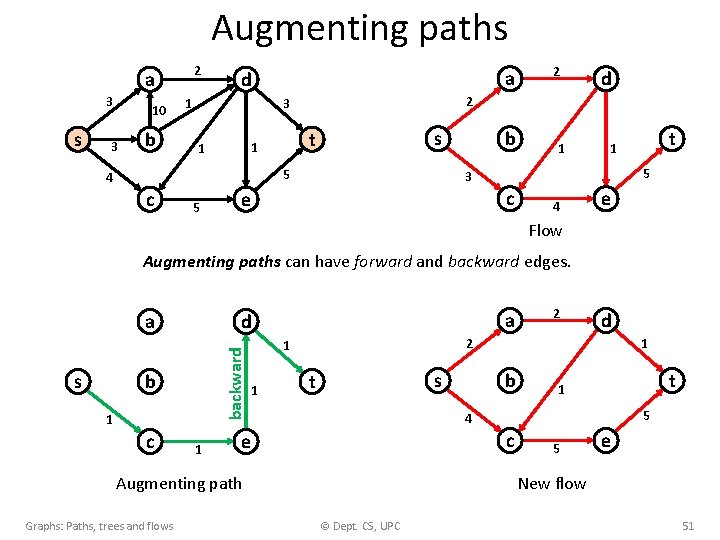
Augmenting paths 2 a 3 s 10 3 b a d s t 1 1 5 4 c 5 d 2 3 1 2 b 1 5 3 c e t 1 4 e Flow Augmenting paths can have forward and backward edges. s b 1 c a d backward a 1 s t 1 b t 1 5 4 c e Augmenting path Graphs: Paths, trees and flows d 2 1 1 2 5 e New flow © Dept. CS, UPC 51

Augmenting paths • Graphs: Paths, trees and flows © Dept. CS, UPC 52

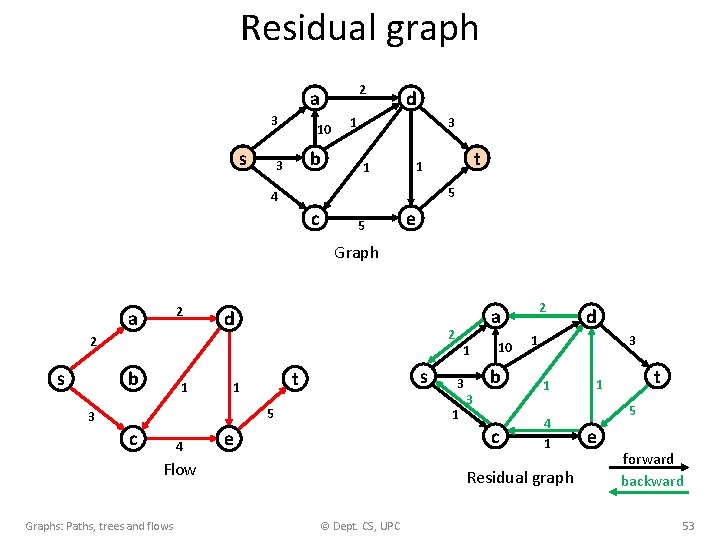
Residual graph 2 a 3 s 10 b 3 d 3 1 1 t 1 5 4 c 5 e Graph 2 a d 2 2 s b 1 s t 1 5 3 c 4 Flow Graphs: Paths, trees and flows 1 3 1 e 2 a 10 3 1 b 1 c 4 1 3 Residual graph © Dept. CS, UPC d t 1 5 e forward backward 53

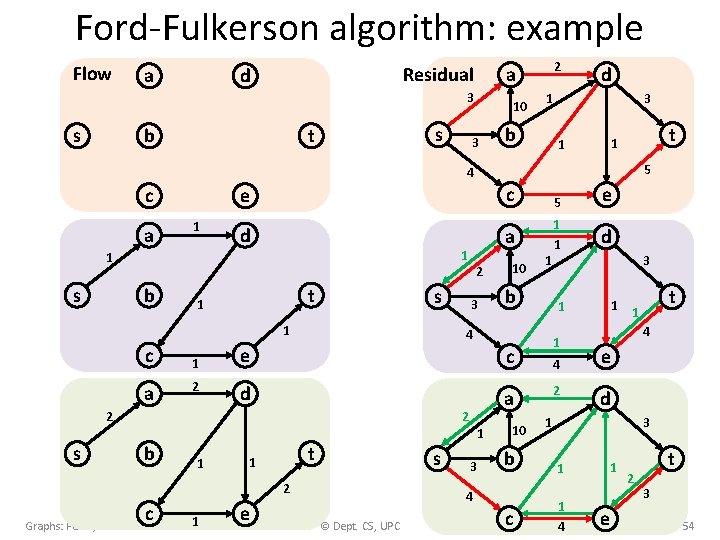
Ford-Fulkerson algorithm: example Flow a Residual d 3 s b s t 2 a 10 3 d 3 1 b t 1 1 5 4 c a 1 e c 5 e d a 1 1 d 1 1 s b t 1 s 1 c a 1 2 3 e 1 d t 1 s 2 c Graphs: Paths, trees and flows 1 e 1 b 1 3 10 2 1 t 1 4 e d 3 1 b 1 c 1 4 4 © Dept. CS, UPC 4 a 1 3 1 c 2 b 10 4 2 s 2 1 e 2 t 3 54

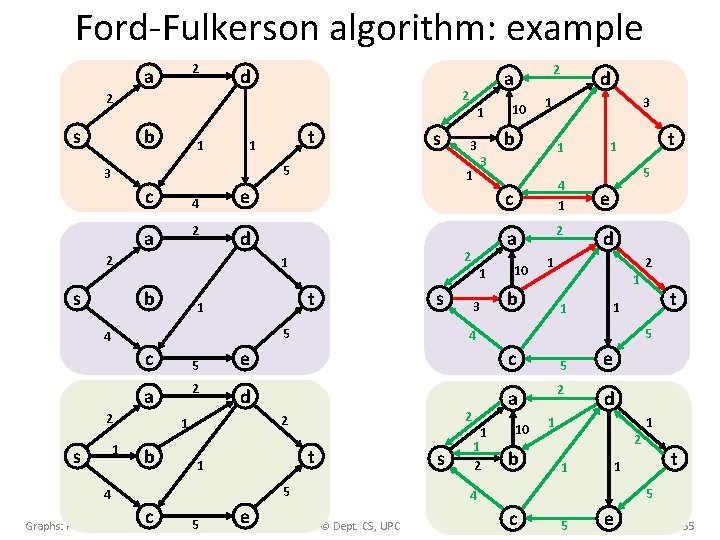
Ford-Fulkerson algorithm: example 2 a d 2 2 s b 1 s 5 3 c 4 2 a s d t 1 s 5 4 c 5 2 a 2 1 10 2 t e 5 e d 1 1 1 s t 1 1 1 2 10 b 5 2 e d 1 2 1 1 t 1 5 4 © Dept. CS, UPC 2 5 a 1 2 b d 2 5 c 4 1 t 1 4 5 c 1 a 3 3 1 d b c 4 Graphs: Paths, trees and flows 10 e 1 b 3 2 1 b 1 1 e 2 s t 1 2 a c 5 e 55

Ford-Fulkerson algorithm Graphs: Paths, trees and flows © Dept. CS, UPC 56

Ford-Fulkerson algorithm: complexity • Graphs: Paths, trees and flows © Dept. CS, UPC 57

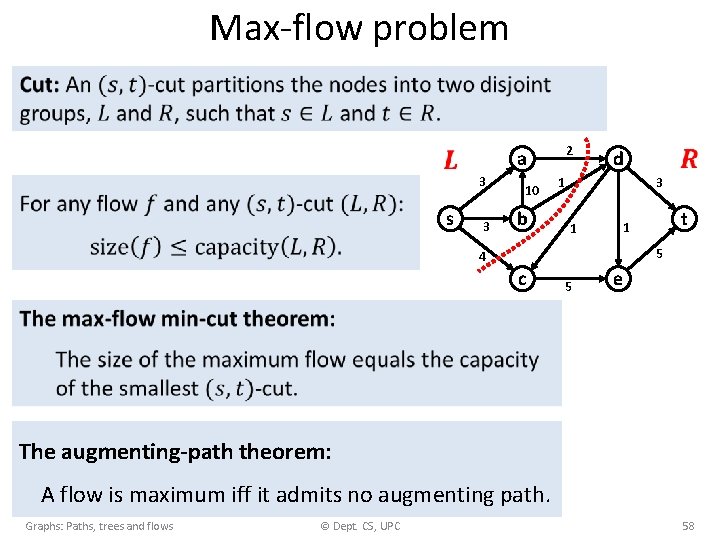
Max-flow problem 2 a 3 s 3 10 b d 3 1 1 t 1 5 4 c 5 e The augmenting-path theorem: A flow is maximum iff it admits no augmenting path. Graphs: Paths, trees and flows © Dept. CS, UPC 58

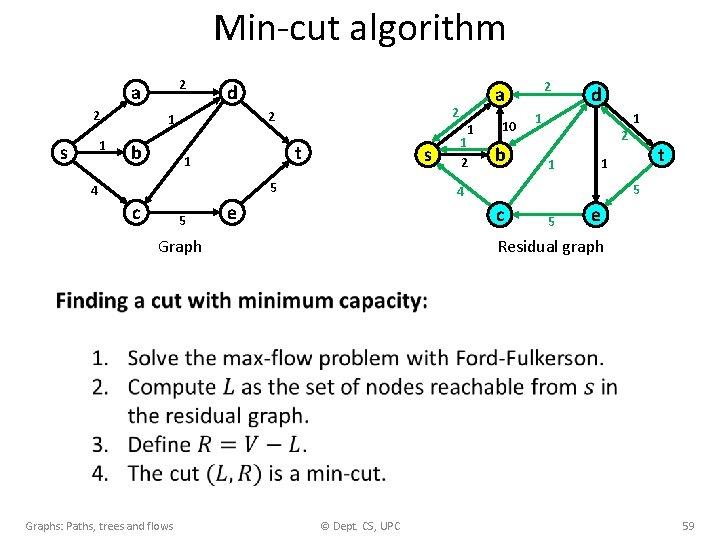
Min-cut algorithm 2 a 2 1 s d b 2 2 1 t 1 s 5 4 c 5 2 a 1 1 2 10 b d 1 2 1 t 1 5 4 e 1 c 5 e Residual graph Graphs: Paths, trees and flows © Dept. CS, UPC 59

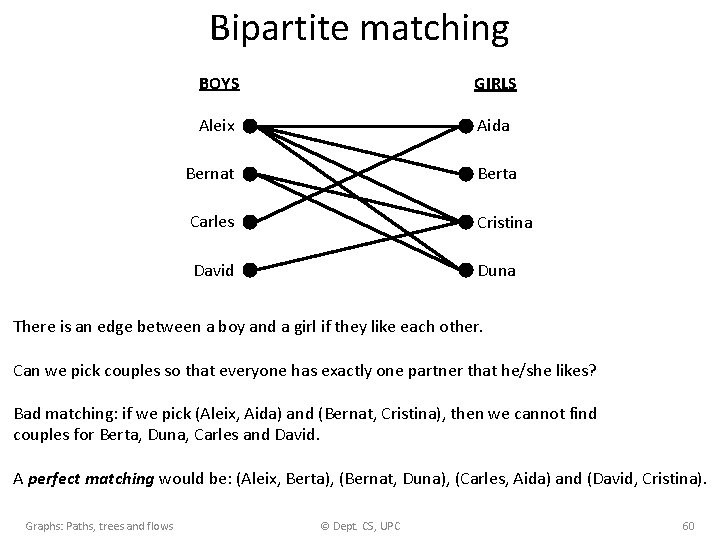
Bipartite matching BOYS GIRLS Aleix Aida Bernat Berta Carles Cristina David Duna There is an edge between a boy and a girl if they like each other. Can we pick couples so that everyone has exactly one partner that he/she likes? Bad matching: if we pick (Aleix, Aida) and (Bernat, Cristina), then we cannot find couples for Berta, Duna, Carles and David. A perfect matching would be: (Aleix, Berta), (Bernat, Duna), (Carles, Aida) and (David, Cristina). Graphs: Paths, trees and flows © Dept. CS, UPC 60

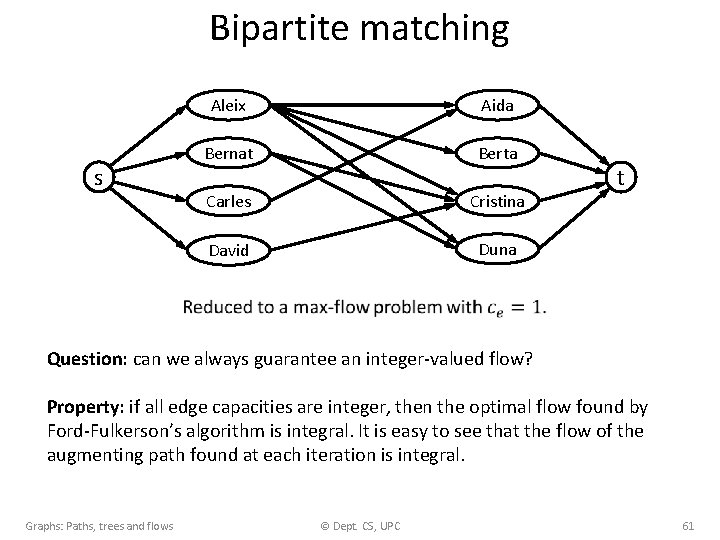
Bipartite matching s Aleix Aida Bernat Berta Carles Cristina David Duna t Question: can we always guarantee an integer-valued flow? Property: if all edge capacities are integer, then the optimal flow found by Ford-Fulkerson’s algorithm is integral. It is easy to see that the flow of the augmenting path found at each iteration is integral. Graphs: Paths, trees and flows © Dept. CS, UPC 61

Extensions of Max-Flow • Graphs: Paths, trees and flows © Dept. CS, UPC 62

EXERCISES Graphs: Paths, trees and flows © Dept. CS, UPC 63

Dijkstra (from [DPV 2008]) A 1 4 8 E 5 B 2 6 F 6 1 1 C 2 G D 1 1 4 H Run Dijkstra’s algorithm starting at node A: – Draw a table showing the intermediate distance values of all the nodes at each iteration – Show the final shortest-path tree Graphs: Paths, trees and flows © Dept. CS, UPC 64

Bellman-Ford (from [DPV 2008]) -2 A C 7 4 6 B S -4 -2 -1 I 1 5 6 1 G 2 H 3 D 3 F -2 E 1 Run Bellman-Ford algorithm starting at node S: – Draw a table showing the intermediate distance values of all the nodes at each iteration – Show the final shortest-path tree Graphs: Paths, trees and flows © Dept. CS, UPC 65

New road (from [DPV 2008]) • Graphs: Paths, trees and flows © Dept. CS, UPC 66

Minimum Spanning Trees 10 J 12 8 K 5 C 3 7 10 9 D 3 10 9 8 B 2 13 I 6 A E 12 Graphs: Paths, trees and flows • Calculate the shortest path tree from node A using Dijkstra’s algorithm. H 7 G 6 10 8 F • Calculate the MST using Prim’s algorithm. Indicate the sequence of edges added to the tree and the evolution of the priority queue. • Calculate the MST using Kruskal’s algorithm. Indicate the sequence of edges added to the tree and the evolution of the disjoint sets. In case of a tie between two edges, try to select the one that is not in Prim’s tree. © Dept. CS, UPC 67

Flow network (from [DVP 2008]) 6 S 1 10 A 4 D 2 1 2 B 20 10 G 12 6 2 C E 5 5 F 4 T • Find the maximum flow from S to T. Give a sequence of augmenting paths that lead to the maximum flow. • Draw the residual graph after finding the maximum flow. • Find a minimum cut between S and T. Graphs: Paths, trees and flows © Dept. CS, UPC 68

Contagious disease The island of Sodor is home to a large number of towns and villages, connected by an extensive rail network. Recently, several cases of a deadly contagious disease (Covid 19) have been reported in the village of Ffarquhar. The controller of the Sodor railway plans to close down certain railway stations to prevent the disease from spreading to Tidmouth, his home town. No trains can pass through a closed station. To minimize expense (and public notice), he wants to close down as few stations as possible. However, he cannot close the Ffarquhar station, because that would expose him to the disease, and he cannot close the Tidmouth station, because then he couldn’t visit his favorite pub. Describe and analyze an algorithm to find the minimum number of stations that must be closed to block all rail travel from Ffarquhar to Tidmouth. The Sodor rail network is represented by an undirected graph, with a vertex for each station and an edge for each rail connection between two stations. Two special vertices F and T represent the stations in Ffarquhar and Tidmouth. For example, given the following input graph, your algorithm should return the number 2. F Graphs: Paths, trees and flows T © Dept. CS, UPC Source: Jeff Erickson, Algorithms, UIUC, 2015. 69

Blood transfusion Enthusiastic celebration of a sunny day at a prominent northeastern university has resulted in the arrival at the university's medical clinic of 169 students in need of emergency treatment. Each of the 169 students requires a transfusion of one unit of whole blood. The clinic has supplies of 170 units of whole blood. The number of units of blood available in each of the four major blood groups and the distribution of patients among the groups is summarized below. Blood type A B O AB Supply 46 34 45 45 Demand 39 38 42 50 Type A patients can only receive type A or O; type B patients can receive only type B or O; type O patients can receive only type O; and type AB patients can receive any of the four types. Give a maxflow formulation that determines a distribution that satisfies the demands of a maximum number of patients. Can we have enough blood units for all the students? Source: Sedgewick and Wayne, Algorithms, 4 th edition, 2011. Graphs: Paths, trees and flows © Dept. CS, UPC 70

Edge-disjoint paths • Graphs: Paths, trees and flows © Dept. CS, UPC 71