Graphs Shortest paths Jordi Cortadella and Jordi Petit

Graphs: Shortest paths Jordi Cortadella and Jordi Petit Department of Computer Science

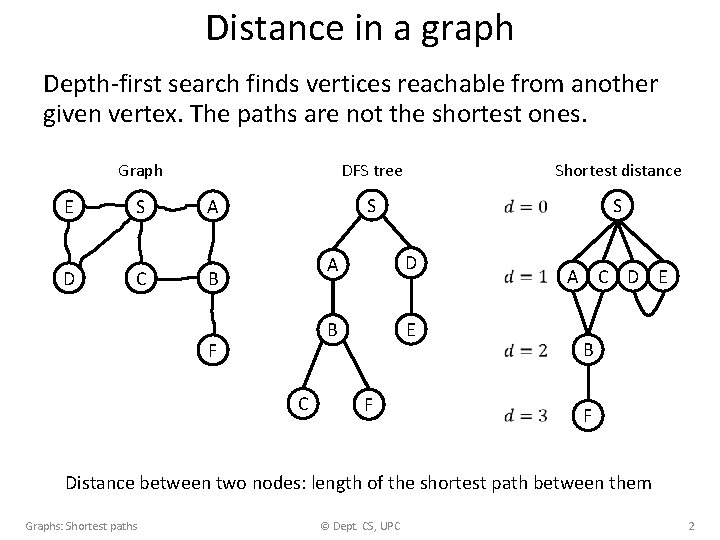
Distance in a graph Depth-first search finds vertices reachable from another given vertex. The paths are not the shortest ones. Graph E D S C A B F C DFS tree Shortest distance S S A D B E F A C D E B F Distance between two nodes: length of the shortest path between them Graphs: Shortest paths © Dept. CS, UPC 2

Breadth-first search Similar to a wave propagation Graphs: Shortest paths © Dept. CS, UPC 3

Breadth-first search Graphs: Shortest paths © Dept. CS, UPC 4

Breadth-first search 6 5 4 3 2 3 4 5 6 5 4 3 2 1 2 3 4 5 4 3 2 1 0 1 2 3 4 5 4 3 2 1 2 3 4 5 6 5 4 3 2 3 4 5 6 Graphs: Shortest paths © Dept. CS, UPC 5

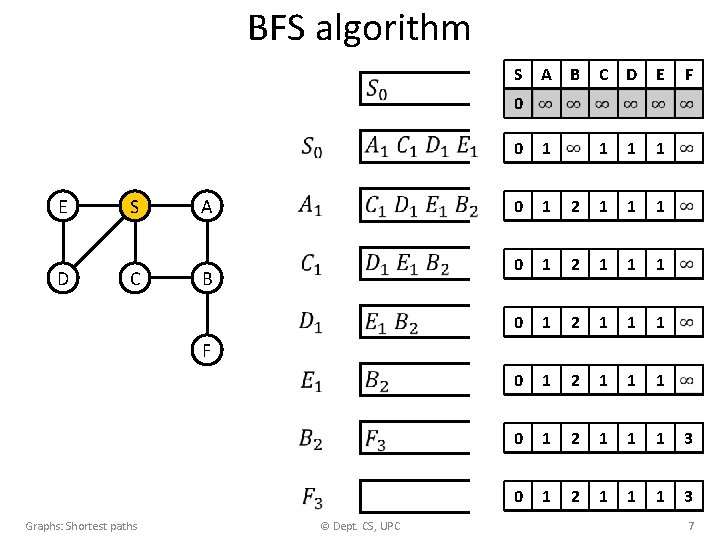
BFS algorithm • Graphs: Shortest paths © Dept. CS, UPC 6

BFS algorithm S A B C D E F 0 1 1 0 1 2 1 1 1 0 1 2 1 1 1 3 0 E D S C A B F Graphs: Shortest paths © Dept. CS, UPC 7

BFS algorithm Graphs: Shortest paths © Dept. CS, UPC 8

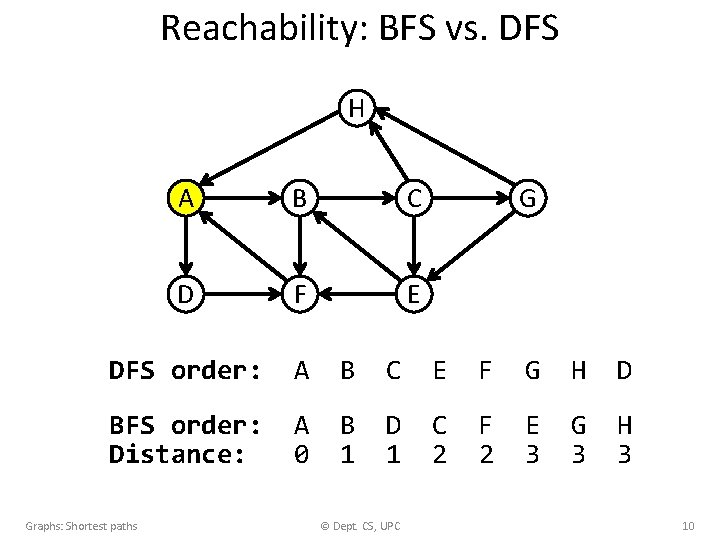
Reachability: BFS vs. DFS Graphs: Shortest paths © Dept. CS, UPC 9

Reachability: BFS vs. DFS H A B C D F E DFS order: A B C E F G H D BFS order: Distance: A 0 B 1 D 1 C 2 F 2 E 3 G 3 H 3 Graphs: Shortest paths © Dept. CS, UPC G 10

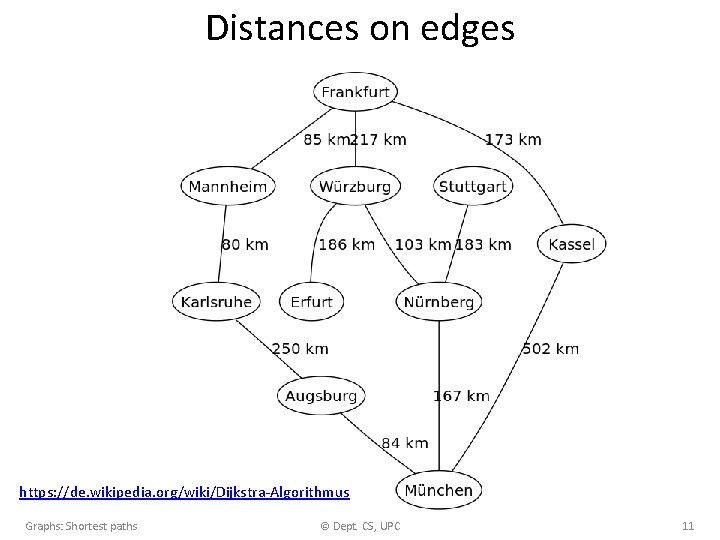
Distances on edges https: //de. wikipedia. org/wiki/Dijkstra-Algorithmus Graphs: Shortest paths © Dept. CS, UPC 11

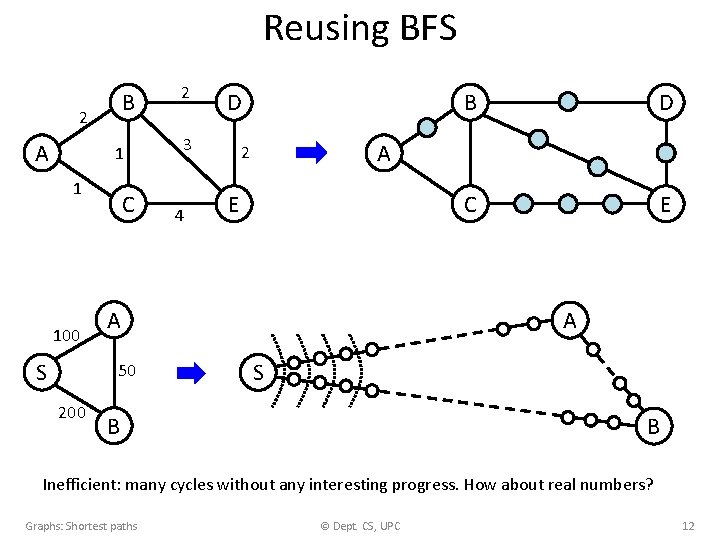
Reusing BFS B 2 A 1 1 100 S C D 3 4 B D C E A 2 E A 50 200 2 A S B B Inefficient: many cycles without any interesting progress. How about real numbers? Graphs: Shortest paths © Dept. CS, UPC 12

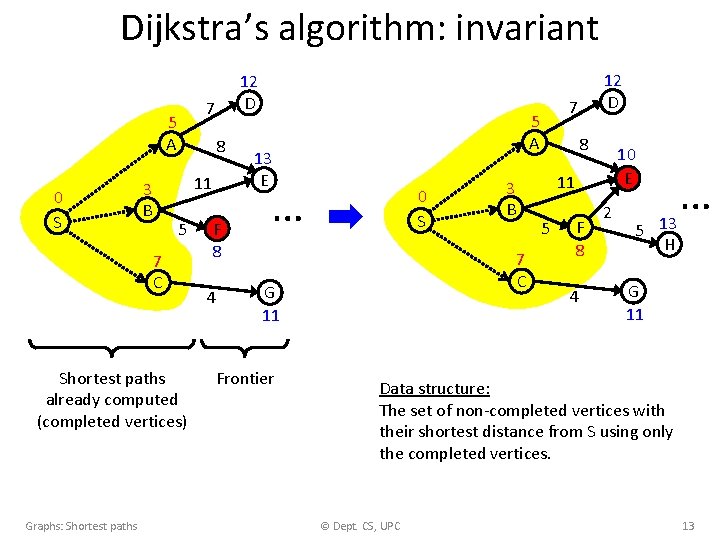
Dijkstra’s algorithm: invariant 7 5 A 0 S 8 11 3 B 5 7 C Shortest paths already computed (completed vertices) Graphs: Shortest paths 12 D F 8 4 … 0 S 8 10 13 E 11 3 B 5 7 C G 11 Frontier 7 5 A 13 E 12 D F 8 4 2 5 13 H … G 11 Data structure: The set of non-completed vertices with their shortest distance from S using only the completed vertices. © Dept. CS, UPC 13

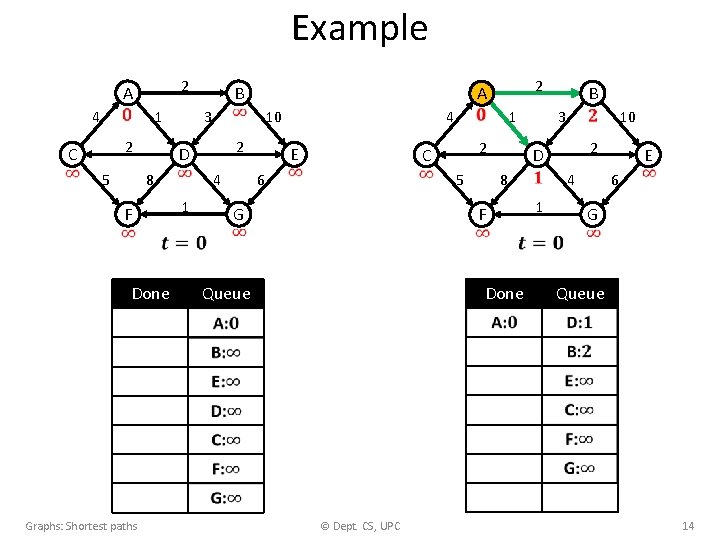
Example 2 A 4 1 2 C 5 10 2 D F Done 4 1 2 A 3 8 Graphs: Shortest paths B 4 E 1 2 C 6 5 G 8 Done © Dept. CS, UPC 3 10 2 D F Queue B 4 1 E 6 G Queue 14

Example 2 A 4 1 2 C 5 10 2 D F Done 4 1 2 A 3 8 Graphs: Shortest paths B 4 E 1 2 C 6 5 G 8 Done © Dept. CS, UPC 3 10 2 D F Queue B 4 1 E 6 G Queue 15

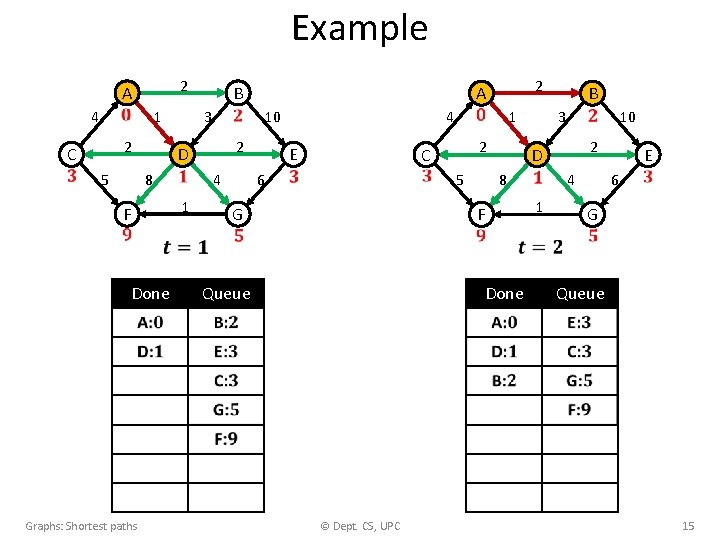
Example 2 A 4 1 2 C 5 B 3 10 2 D 8 F Done 4 1 2 A 4 E 1 2 C 6 5 G 3 10 2 D 8 F Done Queue B 4 1 E 6 G Queue G: 5 Graphs: Shortest paths © Dept. CS, UPC 16

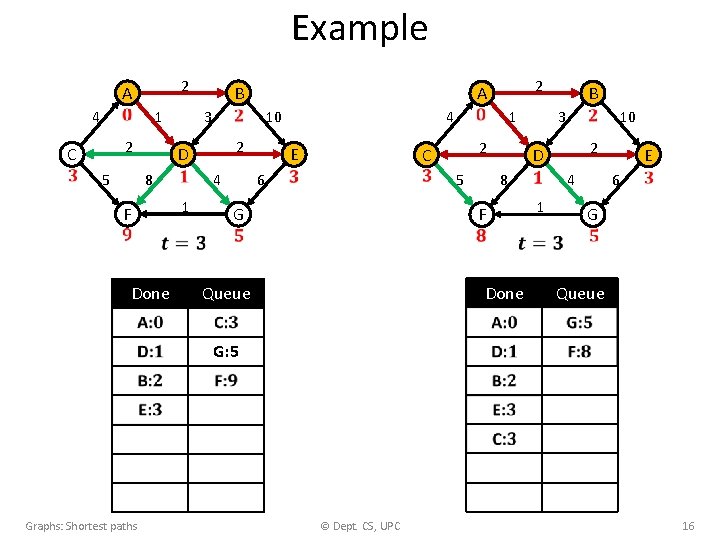
Example 2 A 4 1 2 C 5 3 8 F Done Graphs: Shortest paths 2 4 10 D 2 A B 1 2 C E 5 6 Queue 8 Done © Dept. CS, UPC 3 10 2 D F G B 4 1 E 6 G Queue 17

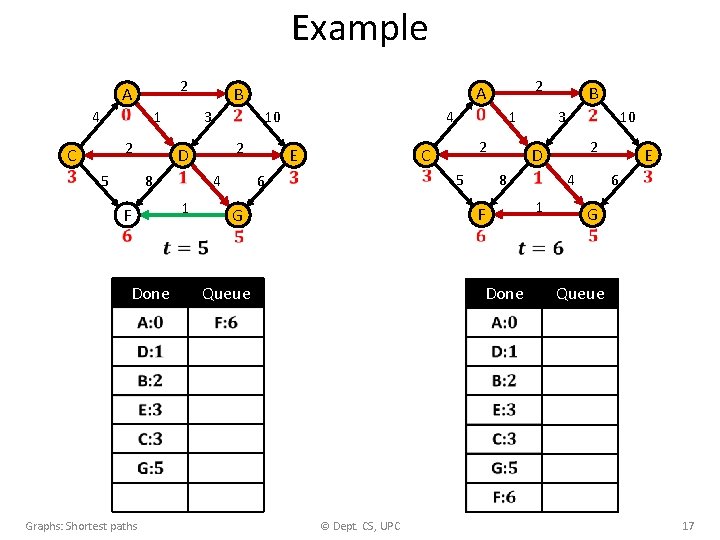
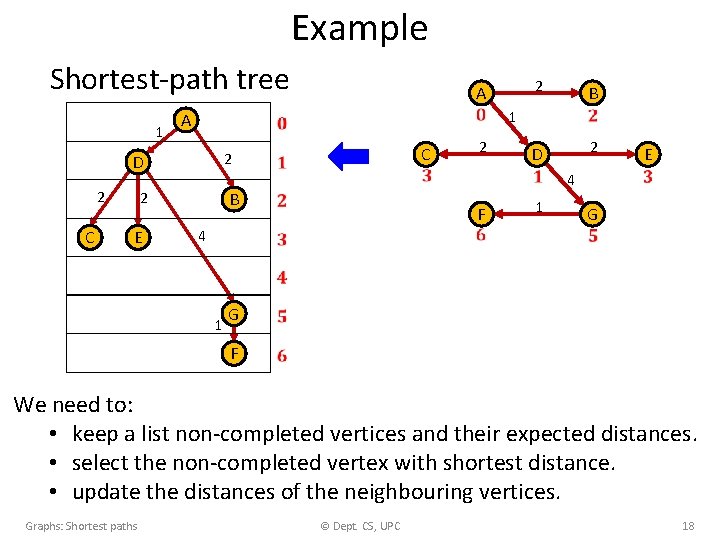
Example Shortest-path tree 1 C C 2 B 2 D 2 E 4 B 2 E 2 1 A D 2 A F 1 G 4 1 G F We need to: • keep a list non-completed vertices and their expected distances. • select the non-completed vertex with shortest distance. • update the distances of the neighbouring vertices. Graphs: Shortest paths © Dept. CS, UPC 18

Dijkstra’s algorithm for shortest paths Graphs: Shortest paths © Dept. CS, UPC 19

Dijkstra’s algorithm: complexity Graphs: Shortest paths © Dept. CS, UPC 20

Dijkstra’s algorithm: complexity Implementation deletemin insert/ decreasekey Dijkstra’s complexity Vector Binary heap Graphs: Shortest paths © Dept. CS, UPC 21

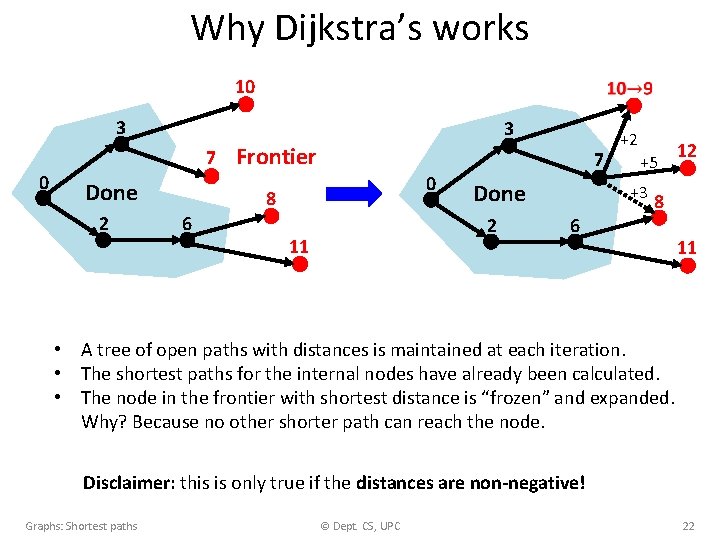
Why Dijkstra’s works 10 3 3 7 0 Done 2 Frontier 0 8 6 7 Done 2 11 +2 +5 +3 6 12 8 11 • A tree of open paths with distances is maintained at each iteration. • The shortest paths for the internal nodes have already been calculated. • The node in the frontier with shortest distance is “frozen” and expanded. Why? Because no other shorter path can reach the node. Disclaimer: this is only true if the distances are non-negative! Graphs: Shortest paths © Dept. CS, UPC 22

Graphs with negative edges • 3 A -2 S 4 Graphs: Shortest paths Dijkstra would say that the shortest path S A has length=3. B © Dept. CS, UPC 23

Graphs with negative edges • Graphs: Shortest paths © Dept. CS, UPC 24

Bellman-Ford algorithm Graphs: Shortest paths © Dept. CS, UPC 25

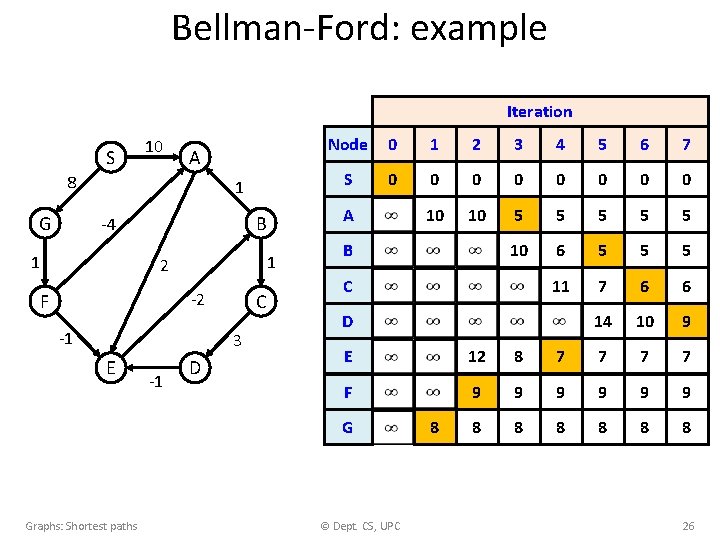
Bellman-Ford: example Iteration S 10 A 8 G 1 1 1 2 -2 F -1 C 3 E -1 D 0 1 2 3 4 5 6 7 S 0 0 0 0 10 10 5 5 5 10 6 5 5 5 11 7 6 6 14 10 9 A B -4 Node B C D E 12 8 7 7 F 9 9 9 8 8 8 G Graphs: Shortest paths © Dept. CS, UPC 8 26

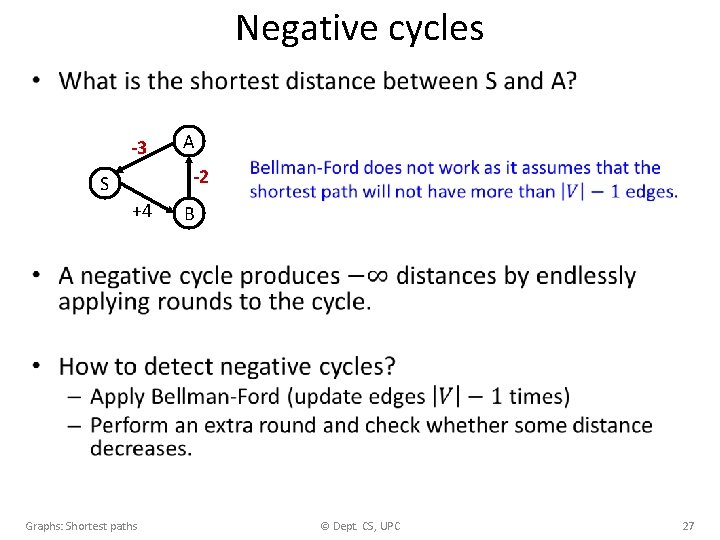
Negative cycles • -3 A -2 S +4 Graphs: Shortest paths B © Dept. CS, UPC 27

Shortest paths in DAGs • Graphs: Shortest paths © Dept. CS, UPC 28

DAG shortest paths algorithm Graphs: Shortest paths © Dept. CS, UPC 29

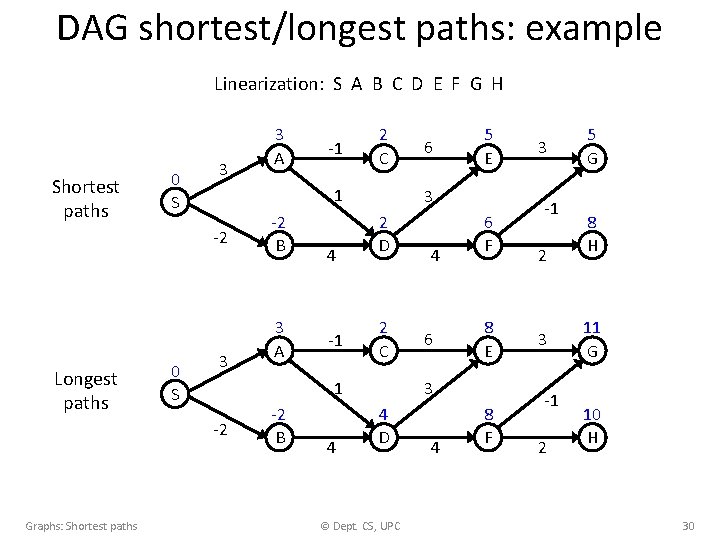
DAG shortest/longest paths: example Linearization: S A B C D E F G H Shortest paths 0 S 3 Longest paths 3 2 C -2 B 3 A 4 -1 -2 B 4 6 5 E 3 2 D 2 C 1 -2 Graphs: Shortest paths -1 1 -2 0 S 3 A 4 6 6 F 8 E 3 4 D © Dept. CS, UPC 4 8 F 3 -1 2 5 G 8 H 11 G 10 H 30

Shortest paths: summary Single-source shortest paths Graph Non-negative edges Algorithm Dijkstra Negative edges DAG Bellman-Ford Topological sort Graphs: Shortest paths © Dept. CS, UPC Complexity 31

EXERCISES Graphs: Shortest paths © Dept. CS, UPC 32

Dijkstra (from [DPV 2008]) A 1 4 8 E 5 B 2 6 F 6 1 1 C 2 G D 1 1 4 H Run Dijkstra’s algorithm starting at node A: – Draw a table showing the intermediate distance values of all the nodes at each iteration – Show the final shortest-path tree Graphs: Shortest paths © Dept. CS, UPC 33

Bellman-Ford (from [DPV 2008]) -2 A C 7 4 6 B S -4 -2 -1 I 1 5 6 1 G 2 H 3 D 3 F -2 E 1 Run Bellman-Ford algorithm starting at node S: – Draw a table showing the intermediate distance values of all the nodes at each iteration – Show the final shortest-path tree Graphs: Shortest paths © Dept. CS, UPC 34

New road (from [DPV 2008]) • Graphs: Shortest paths © Dept. CS, UPC 35

Nesting boxes • Graphs: Shortest paths © Dept. CS, UPC 36