Divide Conquer Jordi Cortadella and Jordi Petit Department

Divide & Conquer Jordi Cortadella and Jordi Petit Department of Computer Science

Divide-and-conquer algorithms • Strategy: – Divide the problem into smaller subproblems of the same type of problem – Solve the subproblems recursively – Combine the answers to solve the original problem • The work is done in three places: – In partitioning the problem into subproblems – In solving the basic cases at the tail of the recursion – In merging the answers of the subproblems to obtain the solution of the original problem Divide & Conquer © Dept. CS, UPC 2

Conventional product of polynomials Example: Divide & Conquer © Dept. CS, UPC 3

Conventional product of polynomials • Divide & Conquer © Dept. CS, UPC 4

Product of polynomials: Divide&Conquer • Shown later Divide & Conquer © Dept. CS, UPC 5

Product of complex numbers • Divide & Conquer © Dept. CS, UPC 6

Product of polynomials with Gauss’s trick Divide & Conquer © Dept. CS, UPC 7

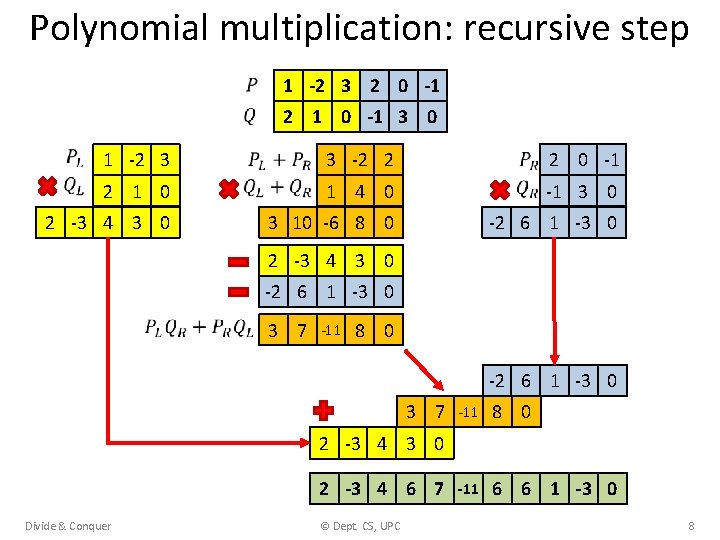
Polynomial multiplication: recursive step 1 -2 3 2 1 0 2 -3 4 3 0 1 -2 3 2 0 -1 2 1 0 -1 3 0 3 -2 2 2 0 -1 1 4 0 -1 3 0 3 10 -6 8 0 -2 6 1 -3 0 2 -3 4 3 0 -2 6 1 -3 0 3 7 -11 8 0 -2 6 1 -3 0 3 7 -11 8 0 -11 6 6 1 -3 0 2 -3 4 6 7 Divide & Conquer © Dept. CS, UPC 8

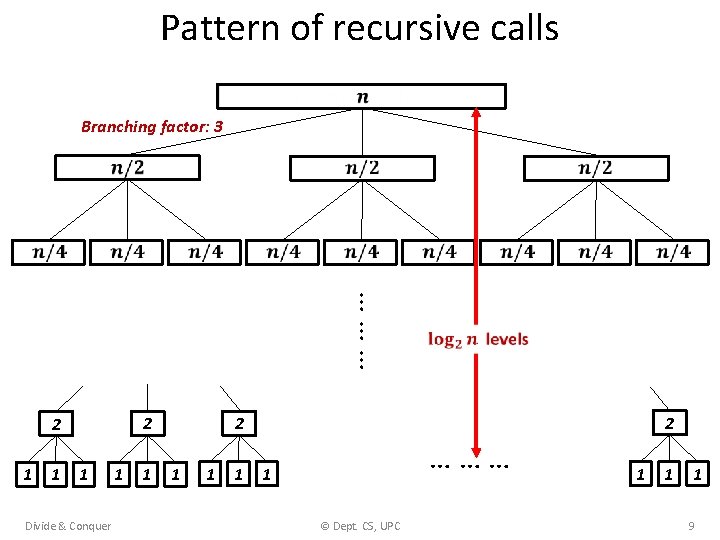
Pattern of recursive calls Branching factor: 3 1 1 Divide & Conquer 1 1 2 2 1 … … … 1 1 1 … … … 1 © Dept. CS, UPC 1 1 1 9

Useful reminders • Divide & Conquer © Dept. CS, UPC 10

Complexity analysis • Divide & Conquer © Dept. CS, UPC 11

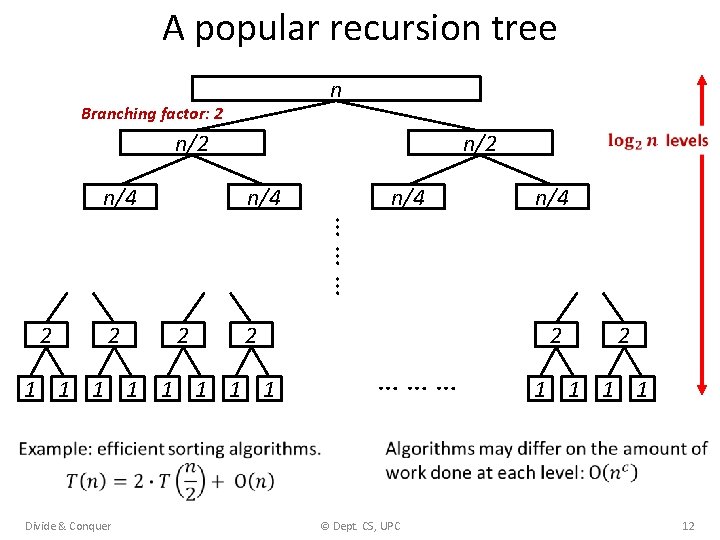
A popular recursion tree n Branching factor: 2 n/4 n/2 n/4 n/4 … … … 2 2 1 1 1 1 2 … … … 2 1 1 Divide & Conquer © Dept. CS, UPC 12

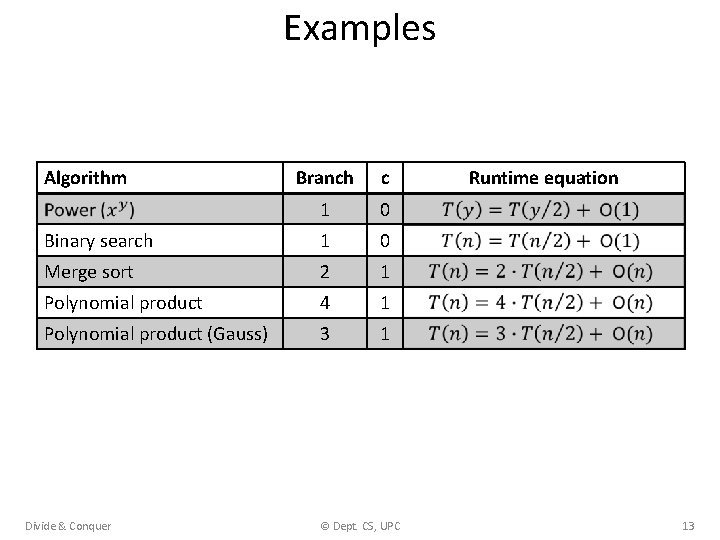
Examples Algorithm Branch c 1 0 Binary search 1 0 Merge sort 2 1 Polynomial product 4 1 Polynomial product (Gauss) 3 1 Divide & Conquer © Dept. CS, UPC Runtime equation 13

Master theorem • Divide & Conquer © Dept. CS, UPC 14

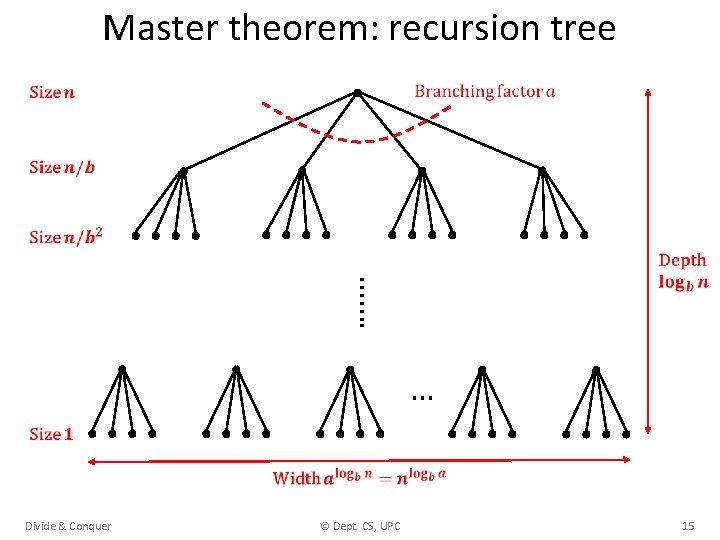
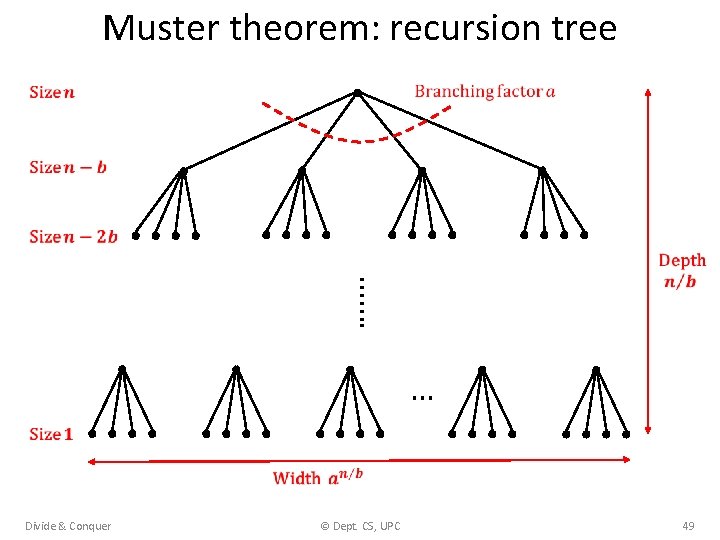
Master theorem: recursion tree ……. … Divide & Conquer © Dept. CS, UPC 15

Master theorem: proof • Divide & Conquer © Dept. CS, UPC 16

Master theorem: proof • Divide & Conquer © Dept. CS, UPC 17

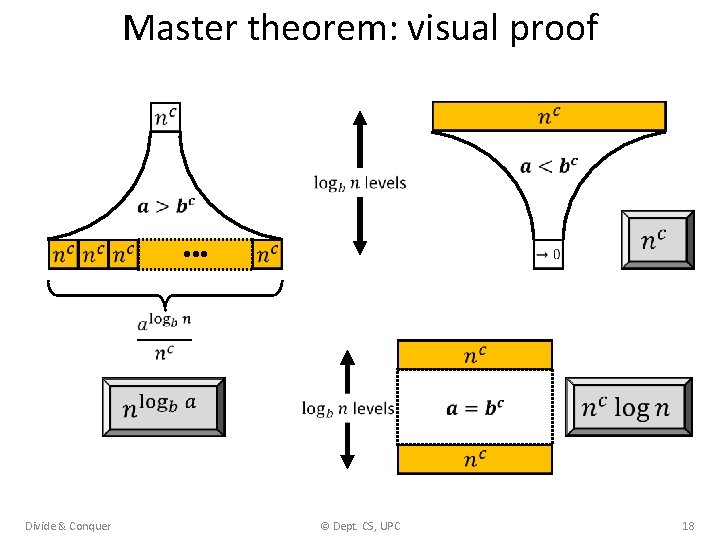
Master theorem: visual proof • • • Divide & Conquer © Dept. CS, UPC 18

Master theorem: examples • Algorithm a c 1 0 Binary search 1 0 Merge sort 2 1 Polynomial product 4 1 Polynomial product (Gauss) 3 1 Runtime equation Complexity Divide & Conquer © Dept. CS, UPC 19

Quick sort (Tony Hoare, 1959) • Divide & Conquer © Dept. CS, UPC 20

Quick sort with Hungarian, folk dance Divide & Conquer © Dept. CS, UPC 21

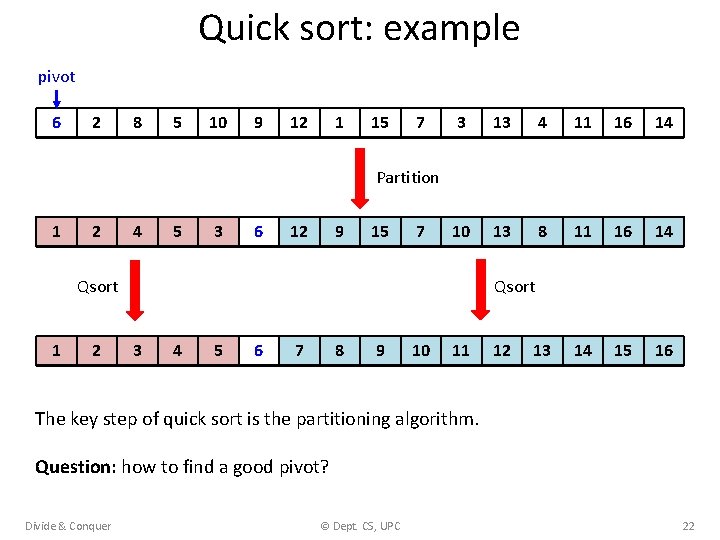
Quick sort: example pivot 6 2 8 5 10 9 12 1 15 7 3 13 4 11 16 14 10 13 8 11 16 14 13 14 15 16 Partition 1 2 4 5 3 6 12 9 15 7 Qsort 1 2 Qsort 3 4 5 6 7 8 9 10 11 12 The key step of quick sort is the partitioning algorithm. Question: how to find a good pivot? Divide & Conquer © Dept. CS, UPC 22

Quick sort https: //en. wikipedia. org/wiki/Quicksort Divide & Conquer © Dept. CS, UPC 23

Quick sort: partition Divide & Conquer © Dept. CS, UPC 24

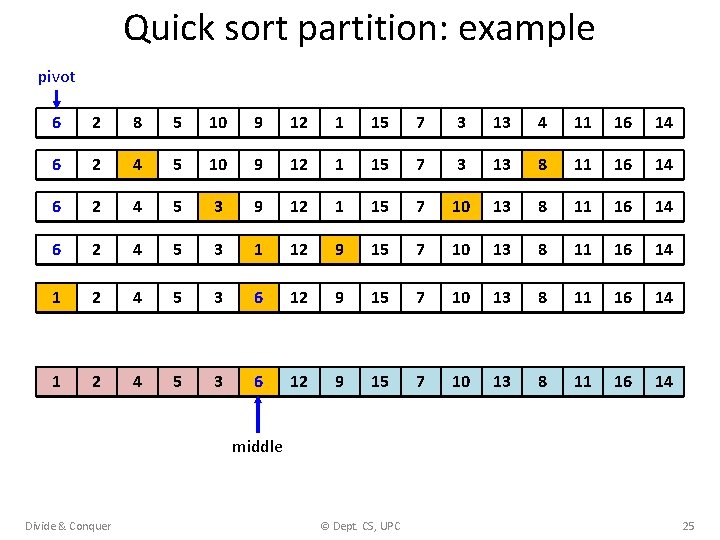
Quick sort partition: example pivot 6 2 8 5 10 9 12 1 15 7 3 13 4 11 16 14 6 2 4 5 10 9 12 1 15 7 3 13 8 11 16 14 6 2 4 5 3 9 12 1 15 7 10 13 8 11 16 14 6 2 4 5 3 1 12 9 15 7 10 13 8 11 16 14 1 2 4 5 3 6 12 9 15 7 10 13 8 11 16 14 middle Divide & Conquer © Dept. CS, UPC 25

Quick sort: algorithm function Qsort(A, left, right) // A[left. . right]: segment to be sorted if left < right then mid = Partition(A, left, right); Qsort(A, left, mid-1); Qsort(A, mid+1, right); Divide & Conquer © Dept. CS, UPC 26

Quick sort: Hoare’s partition Admire a unique piece of art by Hoare: The first swap creates two sentinels. After that, the algorithm flies … Divide & Conquer © Dept. CS, UPC 27

Quick sort partition: example pivot 6 2 8 5 10 9 12 1 15 7 3 13 4 11 16 14 First swap: 4 is a sentinel for R; 6 is a sentinel for L no need to check for boundaries 4 i 2 8 5 10 9 12 1 15 7 3 13 6 j 11 16 14 4 2 3 5 10 9 12 1 15 7 8 13 6 11 16 14 4 2 3 5 1 9 12 10 15 7 8 13 6 11 16 14 j (middle) Divide & Conquer © Dept. CS, UPC 28

Quick sort with Hoare’s partition function Qsort(A, left, right) // A[left. . right]: segment to be sorted if left < right then mid = Hoare. Partition(A, left, right); Qsort(A, left, mid); Qsort(A, mid+1, right); Divide & Conquer © Dept. CS, UPC 29

Quick sort: hybrid approach Divide & Conquer © Dept. CS, UPC 30

Quick sort: complexity analysis • Divide & Conquer © Dept. CS, UPC 31

Quick sort: complexity analysis • Divide & Conquer © Dept. CS, UPC 32

Quick sort: complexity analysis • Divide & Conquer © Dept. CS, UPC 33

Quick sort: complexity analysis summary • Divide & Conquer © Dept. CS, UPC 34

The selection problem • Divide & Conquer © Dept. CS, UPC 35

The selection problem using a heap • Divide & Conquer © Dept. CS, UPC 36

Quick sort with Hoare’s partition function Qsort(A, left, right) // A[left. . right]: segment to be sorted if left < right then mid = Hoare. Partition(A, left, right); Qsort(A, left, mid); Qsort(A, mid+1, right); Divide & Conquer © Dept. CS, UPC 37

Quick select with Hoare’s partition Divide & Conquer © Dept. CS, UPC 38

Quick Select: complexity • Divide & Conquer © Dept. CS, UPC 39

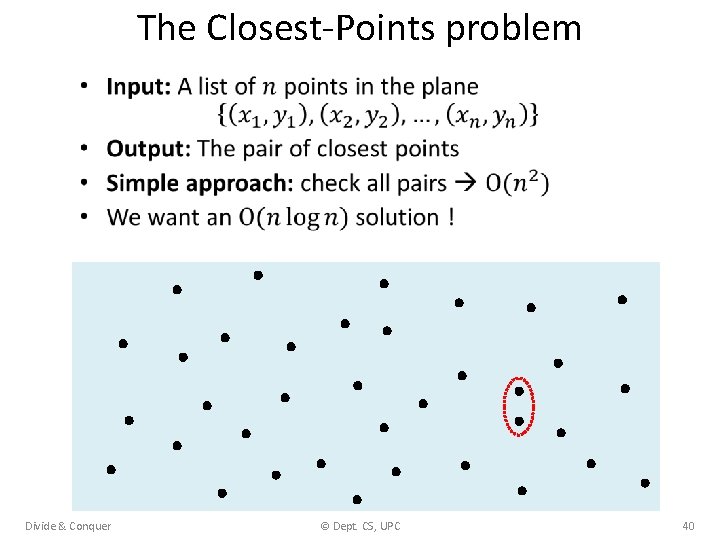
The Closest-Points problem • Divide & Conquer © Dept. CS, UPC 40

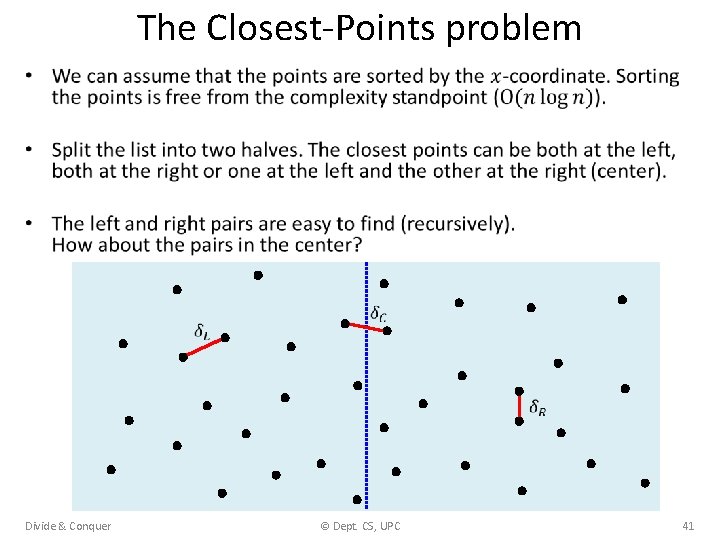
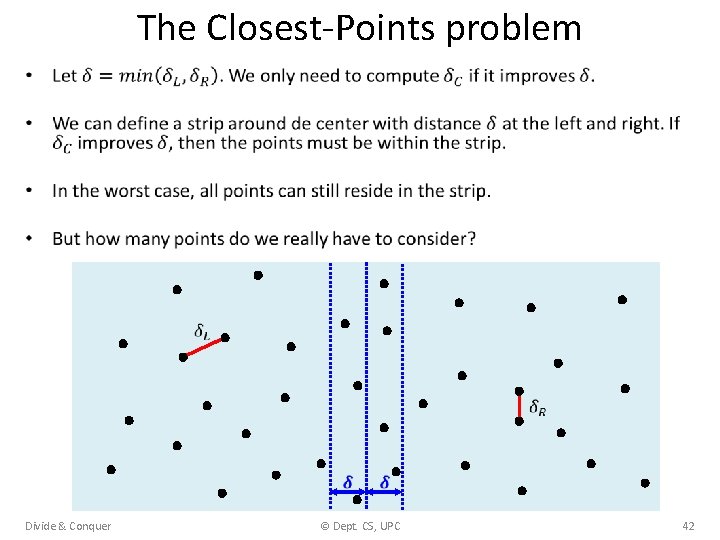
The Closest-Points problem • Divide & Conquer © Dept. CS, UPC 41

The Closest-Points problem • Divide & Conquer © Dept. CS, UPC 42

The Closest-Points problem Divide & Conquer © Dept. CS, UPC 43

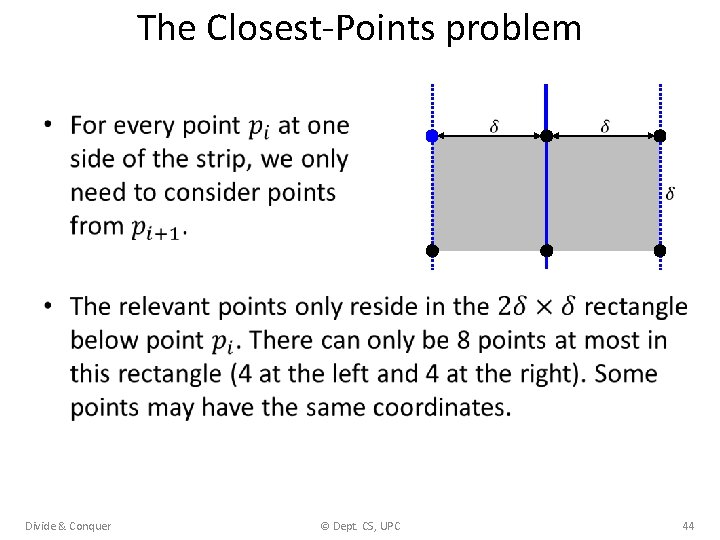
The Closest-Points problem • Divide & Conquer © Dept. CS, UPC 44

The Closest-Points problem: algorithm • Divide & Conquer © Dept. CS, UPC 45

The Closest-Points problem: complexity • Divide & Conquer © Dept. CS, UPC 46

The Closest-Points problem: complexity • Divide & Conquer © Dept. CS, UPC 47

Subtract and Conquer • Divide & Conquer © Dept. CS, UPC 48

Muster theorem: recursion tree ……. … Divide & Conquer © Dept. CS, UPC 49

Muster theorem: proof • Divide & Conquer © Dept. CS, UPC 50

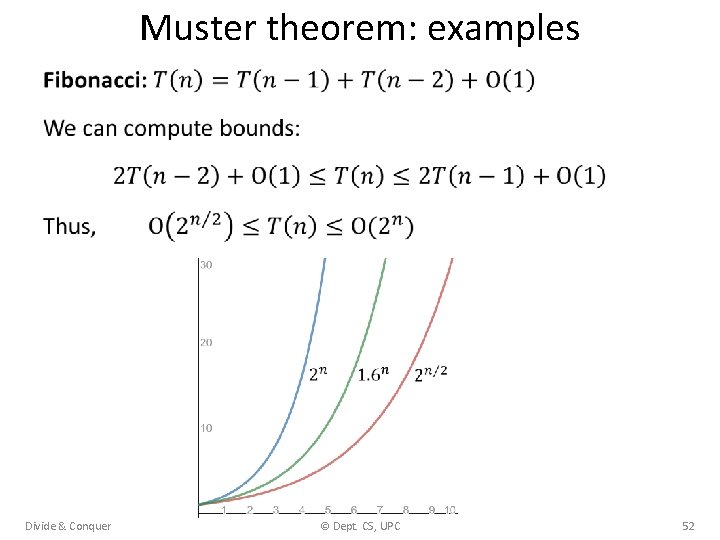
Muster theorem: examples • Divide & Conquer © Dept. CS, UPC 51

Muster theorem: examples • Divide & Conquer © Dept. CS, UPC 52

EXERCICES Divide & Conquer © Dept. CS, UPC 53

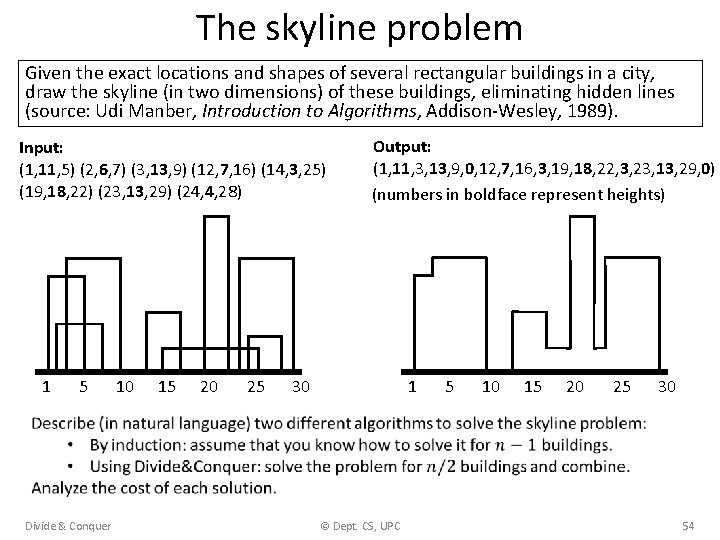
The skyline problem Given the exact locations and shapes of several rectangular buildings in a city, draw the skyline (in two dimensions) of these buildings, eliminating hidden lines (source: Udi Manber, Introduction to Algorithms, Addison-Wesley, 1989). Input: (1, 11, 5) (2, 6, 7) (3, 13, 9) (12, 7, 16) (14, 3, 25) (19, 18, 22) (23, 13, 29) (24, 4, 28) 1 5 10 15 20 25 Output: (1, 11, 3, 13, 9, 0, 12, 7, 16, 3, 19, 18, 22, 3, 23, 13, 29, 0) (numbers in boldface represent heights) 30 1 5 10 15 20 25 30 Divide & Conquer © Dept. CS, UPC 54

A, B or C? • Divide & Conquer © Dept. CS, UPC 55

Crazy sorting • Divide & Conquer © Dept. CS, UPC 56

The majority element • Divide & Conquer © Dept. CS, UPC 57

Breaking into pieces double A(vector<double>& v, int i, int j) { if (i < j) { int x = f(v, i, j); int m = (i+j)/2; return A(v, i, m-1) + A(v, m, j) + A(v, i+1, m) + x; } else { return v[i]; } } double B(vector<double>& v, int i, int j) { if (i < j) { int x = g(v, i, j); int m 1 = i + (j-i+1)/3; int m 2 = i + (j-i+1) 2/3; return B(v, i, m 1 -1) + B(v, m 1, m 2 -1) + B(v, m 2, j) + x; } else { return v[i]; } } Divide & Conquer © Dept. CS, UPC 58

APPENDIX Divide & Conquer © Dept. CS, UPC 59

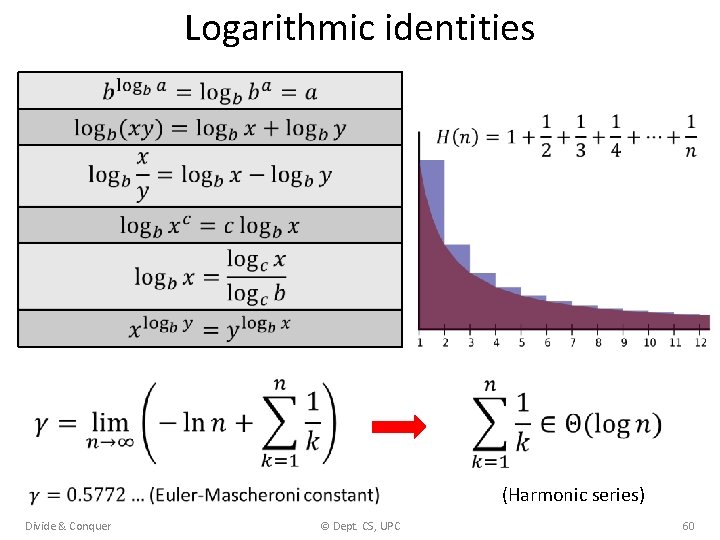
Logarithmic identities (Harmonic series) Divide & Conquer © Dept. CS, UPC 60

Full-history recurrence relation A recurrence that depends on all the previous values of the function. Divide & Conquer © Dept. CS, UPC 61