Frelsningsanteckningar till F 4 sannolikhetslra F 5 sannolikhetslra

Föreläsningsanteckningar till: F 4 sannolikhetslära F 5 sannolikhetslära F 6 sannolikhetslära

Sannolikhetslära Sannolikhet är ett tal mellan noll och ett som beskriver hur stor chans det är att något händer.

Sannolikhetslära Experiment: En process som kan generera olika utfall. Utfall: Ett möjligt resultat av ett experiment Händelse: Ett eller flera utfall.

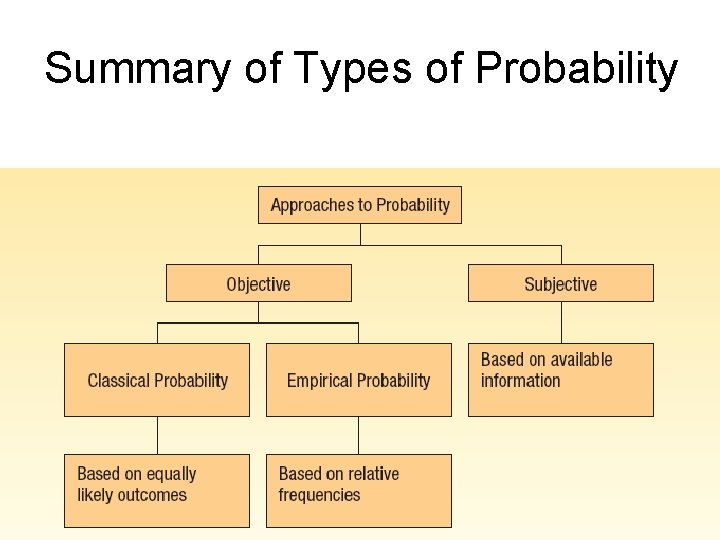
Olika sätt att bestämma sannolikheter Klassisk sannolikhetsteori Fungerar enbart om alla utfall har samma sannolikhet

Olika sätt att bestämma sannolikheter Empirisk sannolikhetsteori Baseras på historiska realiserade utfall. ”The law of large numbers” : Ju fler gånger ett försök utförs desto säkrare blir den empiriska sannolikheten

Empirical Probability - Example On February 1, 2003, the Space Shuttle Columbia exploded. This was the second disaster in 123 space missions for NASA. On the basis of this information, what is the probability that a future mission is successfully completed?

Olika sätt att bestämma sannolikheter Subjektiv sannolikhet Om man inte har erfarenhet att basera en empirisk sannolikhet kan man enbart göra en subjektiv bedömning. Innan olyckan i Harrisburg hade inträffat kunde man inte beräkna en empirisks skattning av sannolikheten för en allvarlig olycka i en kärnkraftreaktor.

Summary of Types of Probability

Ömsesidigt uteslutande: (Mutually exclusive) Ett antal händelser är ömsesidigt uteslutande om enbart en av dem kan hända i varje försök. Kollektivt uttömmande: (Collectively exhaustive) Ett antal händelser är kollektivt uttömmande om minst en av dem måste hända. Oberoende: (Independent) Om utfallet i ett experiment inte påverkar sannolikheten för de olika utfallen i ett annat är de båda experimenten oberoende.

Korstabeller och sannolikheter Vi kan beräkna sannolikheter ur de korstabeller jag visat tidigare.

korstabeller Exempel Vi vill beskriva hur många elever som valt träslöjd respektive textilslöjd Antal elever Kön Flickor Textil- TräTotalt slöjd 40. 35. 75. Pojkar 30. 35. 65. Totalt 70. 140.

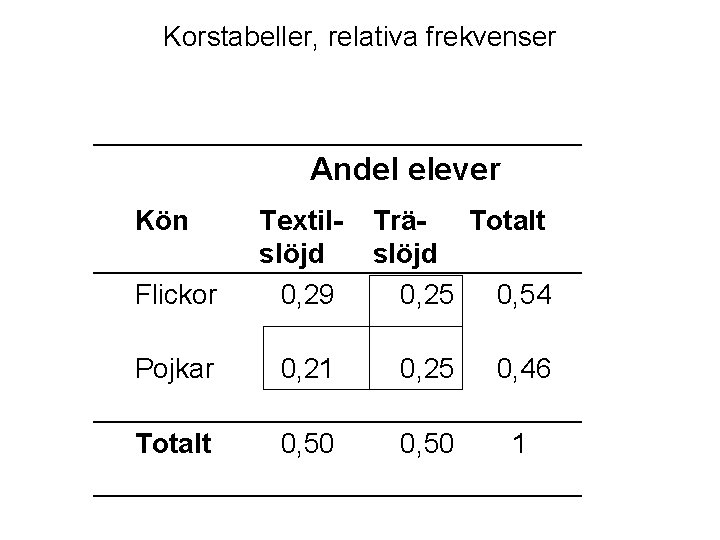
Korstabeller, relativa frekvenser De relativa frekvenserna är lika med sannolikheten att en slumpvist vald elev ska tillhöra den kategorin. Andel elever Kön Flickor Pojkar Totalt Textil- TräTotalt slöjd 0, 29. 0, 25 0, 54. . 0, 21. 0, 25 0, 46. . 0, 50 1. .

Att räkna på sannolikheter Sannolikheten att en händelse inträffar: Komplementregeln Sannolikheten att en slumpvis vald elev är pojke: 0, 46 Sannolikheten att en slumpvis vald elev inte är pojke: 1 – 0, 46 = 0, 54 P(A) = 1 – P(~A)

Att räkna på sannolikheter Sannolikheten att minst en av flera händelser inträffar: Hur stor är sannolikheten att en slumpvis vald elev antingen är pojke eller har valt träslöjd? Adderingsregeln P(A eller B) = P(A) + P(B) – P(A och B) P(pojke eller träslöjd) =P(pojke) + P(träslöjd) – P(pojke som valt träslöjd) 0, 46 + 0, 50 – 0, 25 = 0, 71 Vi kunde också använd komplementregeln. De enda som varken valt träslöjd eller är pojkar är de flickor som valt textilslöjd: 1 – 0, 29 = 0, 71

Korstabeller, relativa frekvenser Andel elever Kön Flickor Pojkar Totalt Textil- TräTotalt slöjd 0, 29. 0, 25 0, 54. . 0, 21. 0, 25 0, 46. . 0, 50 1. .

Speciella adderingsregeln för ömsesidigt uteslutande händelser. Adderingsregel för ömsesidigt uteslutande händelser P(A eller B) = P(A) + P(B) P(pojke eller träslöjd) =P(pojke som valt träslöjd) + P(flicka som valt träslöjd) + P(pojke som valt textilslöjd) 0, 21 + 0, 25 = 0, 71

Frekvenstabeller, kvantitativ variabel Vad är sannolikheten att en elev i denna skola antingen är 7 eller 8 år? Ålder 7 8 9 10 11 12 Antal elever, frekvens 20 23 22 27 23 25 n = 140 Andel elever, relativ frekvens 0, 14 0, 16 0, 19 0, 16 0, 18 1, 00

Betingad sannolikhet Sannolikheten för att något ska inträffa givet att vi vet att något annat har hänt. P(träslöjd) = 70 / 140 = 0, 50 P(träslöjd|pojke) = 35 / 65 = 0, 54

Att räkna på sannolikheter Sannolikheten att båda händelserna inträffar: Hur stor är sannolikheten att en slumpvis vald elev är pojke och har valt träslöjd? Först måste det vara en pojke men vi måste också ta hänsyn till sannolikheten att en pojke skulle välja träslöjd. P(pojke) = 65 / 140 = 0, 46 P(träslöjd|pojke) = 35 / 65 = 0, 54 P(träslöjd och pojke) 0, 46 * 0, 54 = 0, 25 Generella multiplikationsregeln: P(A och B) = P(A) * P(B|A)

Att räkna på sannolikheter Sannolikheten att båda händelserna inträffar: Hur stor är sannolikheten att en slumpvis vald elev är pojke och har valt träslöjd? Det spelar ingen roll vilken händelse vi ser som A och vilken händelse vi ser som B P(träslöjd) = 70 / 140 = 0, 50 P(pojke|träslöjd) = 35 / 70 = 0, 50 P(pojke och träslöjd) 0, 50 * 0, 50 = 0, 25

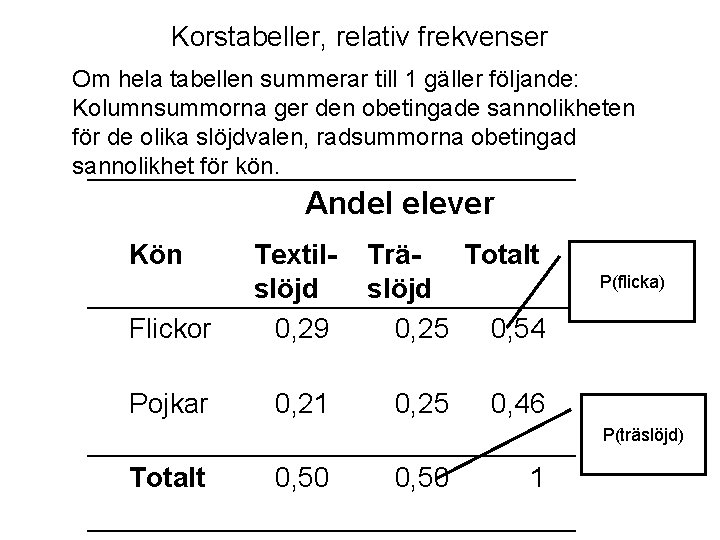
Korstabeller, relativ frekvenser Om hela tabellen summerar till 1 gäller följande: Kolumnsummorna ger den obetingade sannolikheten för de olika slöjdvalen, radsummorna obetingad sannolikhet för kön. Andel elever Kön Flickor Pojkar Totalt Textil- TräTotalt slöjd 0, 29. 0, 25 0, 54. . 0, 21. 0, 25 0, 46. . 0, 50 1. P(flicka) P(träslöjd)

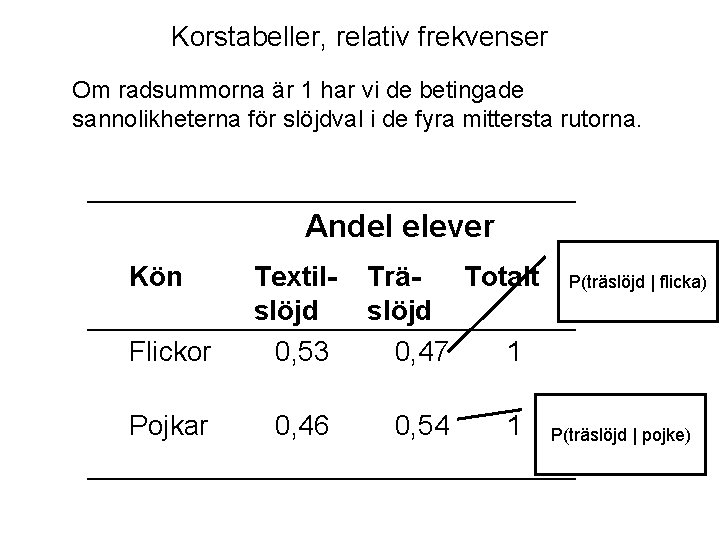
Korstabeller, relativ frekvenser Om radsummorna är 1 har vi de betingade sannolikheterna för slöjdval i de fyra mittersta rutorna. Andel elever Kön Flickor Pojkar Textil- TräTotalt P(träslöjd | flicka) slöjd 0, 53. 0, 47 1. . 0, 46. 0, 54 1. P(träslöjd | pojke).

Korstabeller, relativ frekvenser Om kolumnsummorna är ett har vi de betingade sannolikheterna för kön i de fyra mittersta rutorna. Andel elever Kön Flickor Pojkar Textil- TräTotalt P(flicka | träslöjd) slöjd 0, 57. 0, 50. 0, 43. 0, 50 P(pojke | träslöjd). 1, 00.

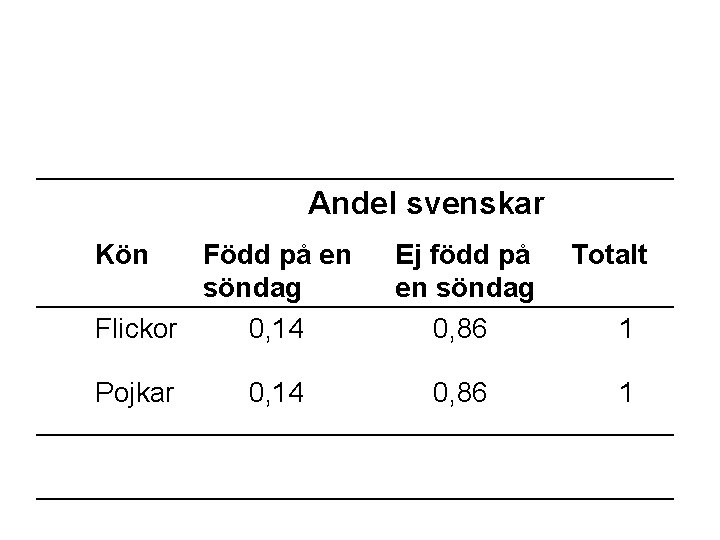
Oberoende och beroende variabler Sannolikheten att välja träslöjd är större för pojkar än för flickor. 0. 54 > 0. 47 Man säger då att: ”variabeln val av slöjdform är beroende av variabeln kön”. Variablerna ”vilken veckodag man är född på” och ”kön” borde dock vara oberoende.

Andel svenskar Kön Född på en söndag Flickor 0, 14. Pojkar 0, 14. Ej född på en söndag 0, 86. Totalt 1. 1.

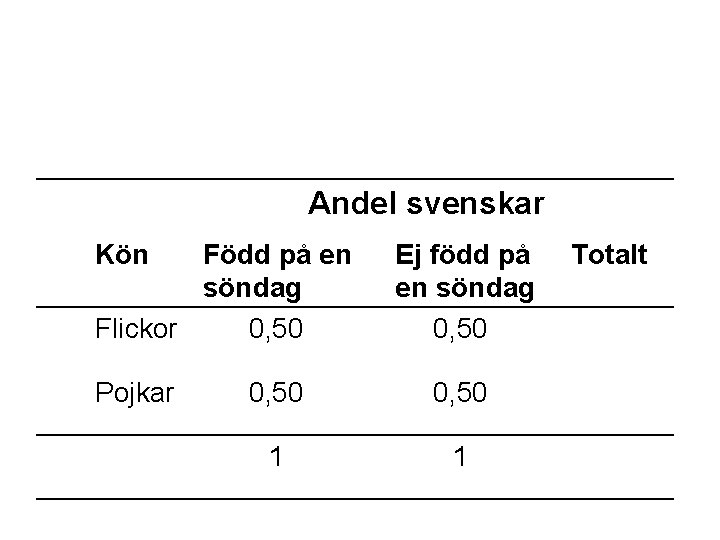
Andel svenskar Kön Född på en söndag Flickor 0, 50. Pojkar Ej född på en söndag 0, 50. 1 , Totalt. .

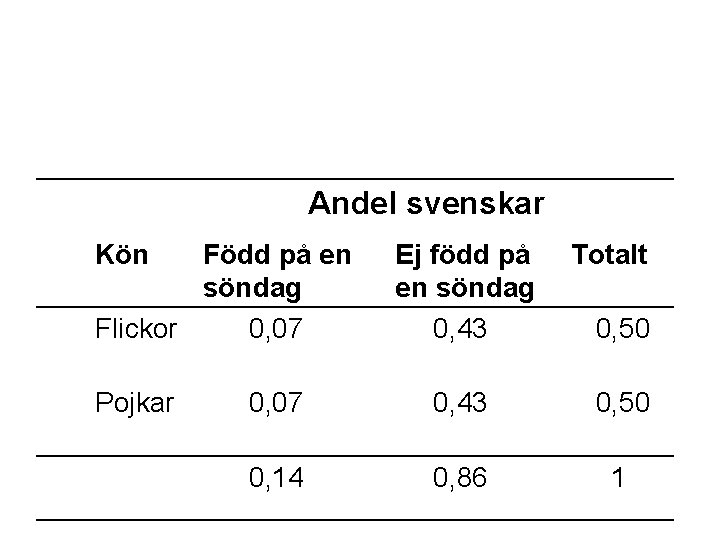
Att räkna på sannolikheter Sannolikheten att båda händelser inträffar: Hur stor är sannolikheten att en slumpvis vald svensk är pojke och född på en söndag? P(pojke) = 0, 50 P(söndag|pojke) = P(söndag)= 0, 14 0, 50 * 0, 14 = 0, 07 Speciella multiplikationsregeln för oberoende variabler: P(A och B) = P(A) * P(B)

Andel svenskar Kön Född på en söndag Flickor 0, 07. Ej född på en söndag 0, 43. Totalt 0, 50. Pojkar 0, 07. 0, 14 , 0, 43. 0, 50 0, 86 , . 1 ,

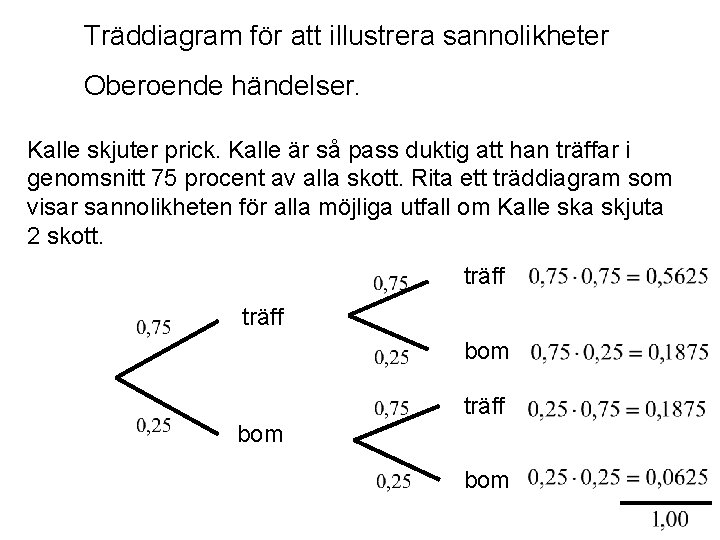
Träddiagram för att illustrera sannolikheter Oberoende händelser. Kalle skjuter prick. Kalle är så pass duktig att han träffar i genomsnitt 75 procent av alla skott. Rita ett träddiagram som visar sannolikheten för alla möjliga utfall om Kalle ska skjuta 2 skott. träff bom

När vi räknade sannolikheterna i träddiagrammet fick vi samma beräkningar som om vi använt multiplikationsregeln för oberoende händelser. Hur stor är sannolikheten att Kalle skjuter en träff? Adderingsregel för ömsesidigt uteslutande händelser: P(A eller B) = P(A) + P(B) P(träff-miss eller miss-träff) = 0, 1875 + 0, 1875 = 0, 375 Hur stor är sannolikheten att Kalle skjuter minst en träff? P(träff-miss eller miss-träff eller träff-träff) = 0, 1875 + 0, 5675 = 0, 9475 Hur stor är sannolikheten att Kalle skjuter 2 bom? Komplementär händelse: 1 - 0, 9475 = 0, 0625

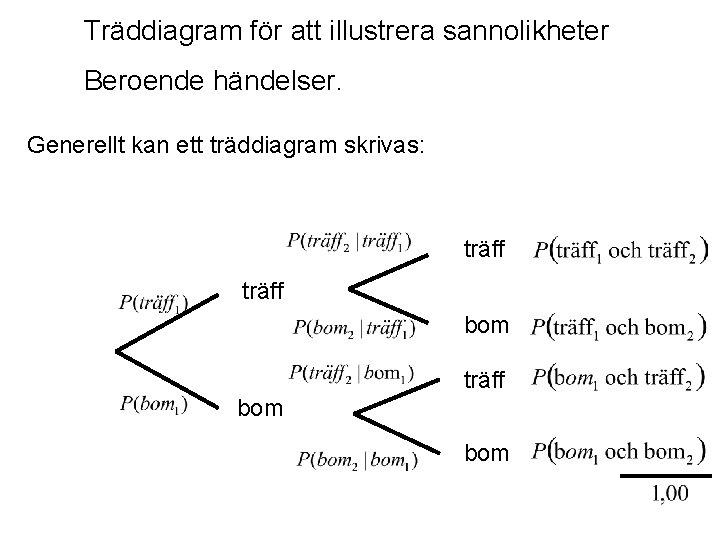
Träddiagram för att illustrera sannolikheter Beroende händelser. Generellt kan ett träddiagram skrivas: träff bom

Träddiagram för att illustrera sannolikheter Beroende händelser. Om man räknar på alla skyttarna i skytteklubben visar det sig att de i genomsnitt träffar hälften av skotten. Men om första skottet träffar ökar sannolikheten att det var en duktig skytt vi valt och då är sannolikheten för träff i andra 0, 6. En slumpvis vald medlem ska skjuta två skott. Illustrera i träddiagram träff bom

Hur stor är sannolikheten att en slumpvis vald skytt i klubben som skjuter två skott får två träff? Generella multiplikationsregeln: P(A och B) = P(A) * P(B|A) P(träff 1 och träff 2) = P(träff 1) * P(träff 2|träff 1) = 0, 5 * 0, 6 = 0, 3 Sannolikheterna i andra förgreningen är betingade på sannolikheterna i första förgreningen Som tidigare kan vi använda adderingsregeln för uteslutande händelser för att beräkna sannolikheten att träffa en gång respektive minst en gång.

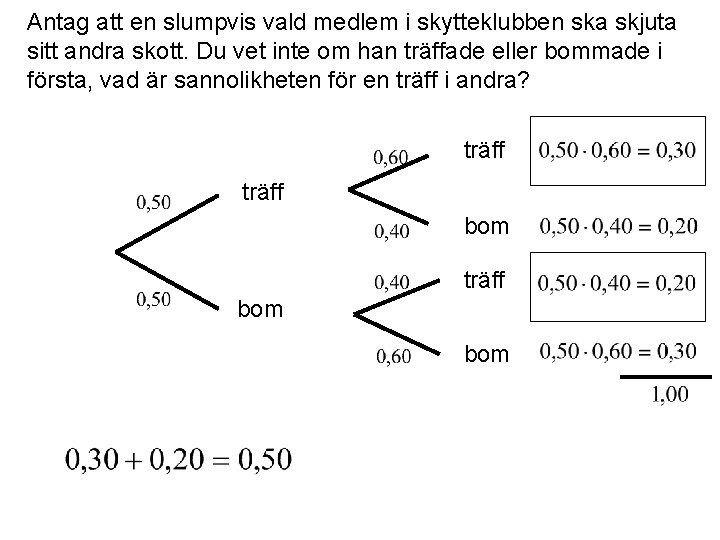
Antag att en slumpvis vald medlem i skytteklubben ska skjuta sitt andra skott. Du vet inte om han träffade eller bommade i första, vad är sannolikheten för en träff i andra? träff bom

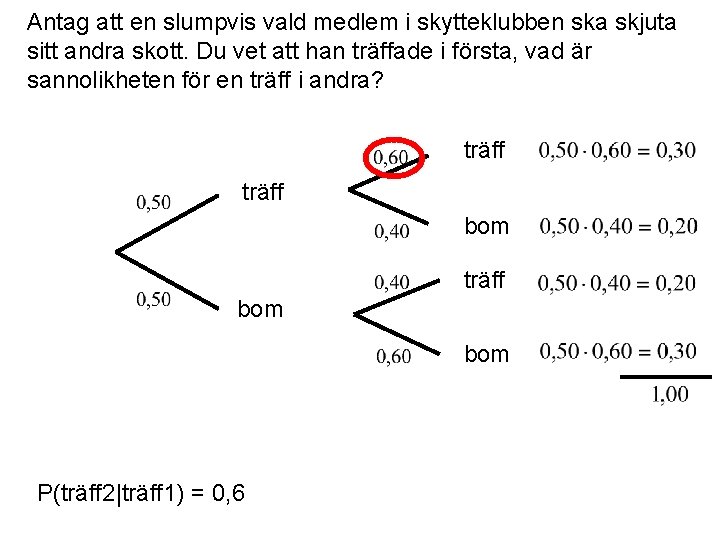
Antag att en slumpvis vald medlem i skytteklubben ska skjuta sitt andra skott. Du vet att han träffade i första, vad är sannolikheten för en träff i andra? träff bom P(träff 2|träff 1) = 0, 6

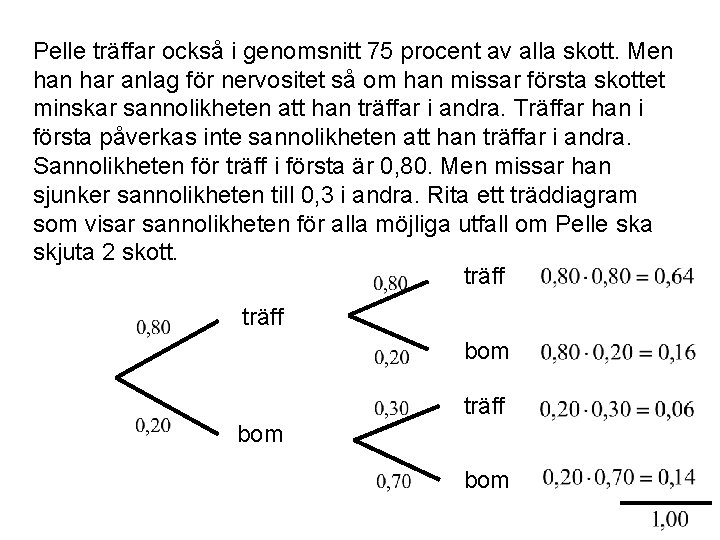
Pelle träffar också i genomsnitt 75 procent av alla skott. Men har anlag för nervositet så om han missar första skottet minskar sannolikheten att han träffar i andra. Träffar han i första påverkas inte sannolikheten att han träffar i andra. Sannolikheten för träff i första är 0, 80. Men missar han sjunker sannolikheten till 0, 3 i andra. Rita ett träddiagram som visar sannolikheten för alla möjliga utfall om Pelle ska skjuta 2 skott. träff bom

Att beräkna antalet möjliga utfall Anta att du slår ett slag med en tärning och singlar en slant, hur många utfall har detta experiment? 1 krona klave 2 3 4 5 6

Multiplikationsformeln: Antalet utfall är lika med antalet utfall för varje delexperiment multiplicerade med varandra. Antalet utfall i experimentet att singla en slant och kasta en tärning: 2 * 6 = 12

Permutationer Ett ordnat urval av element ur en större mängd En curlingklubb har 13 medlemmar varav 6 är tjejer. Man ska välja ut ett damlag med 4 spelare. Hur många olika sätt kan det göras på? Först behöver vi välja ut en etta som slår första stenen, det kan vi göra på 6 sätt. När vi sedan ska välja vem som ska vara tvåa har vi bara 5 att välja på osv. Trots att vi bara hade 6 personer att välja på kunde vi sätta ihop 360 olika permutationer, det blir så många eftersom vi också kan välja att de spelar i olika ordning.

Kan vi hitta någon generell regel för detta? Inom matematiken finns en räkneregel som kallas fakultet vilket innebär att man multiplicerar en siffra med alla heltal som är lägre. Men denna regel ger ett för högt värde vi måste bli av med ettan och tvåan. Lås oss beteckna antalet spelare i klubben med n och antalet deltagare i laget med r

En curlingklubb har 13 medlemmar varav 7 är killar. Man ska nu välja ut ett herrlag med 4 spelare. Hur många olika sätt kan det göras på? Klubben ska skicka ett herrlag och ett damlag till SM hur många olika möjliga laguttagningar finns det? Multiplikationsformeln: 360 * 840 =302 400

Kombinationer Antalet olika sätt att välja ut en delmängd av en större mängd. En curlingklubb har 13 medlemmar varav 6 är tjejer. Man ska välja ut ett damlag med 4 spelare men väljer först senare vem som ska slå vilken sten. Hur många sätt kan det göras på? Nu struntar vi i ordningsföljden. Vi kan konstatera att det finns 4! olika ordningar inom varje lag av fyra spelare. Varje lag ger upphov till 24 olika permutationer så antalet lag ges av antalet permutationer dividerat med 24 dvs 4!

Kombinationsformeln anger hur många kombinationer med r element som kan skapas från en mängd med n element. Permutationsformeln anger hur många ordnade kombinationer med r element som kan skapas från en mängd med n element.

Kombinationer Antalet olika sätt att välja ut en delmängd av en större mängd. En curlingklubb har 13 medlemmar varav 6 är tjejer. Man ska välja ut ett herrlag med 4 spelare men väljer först senare vem som ska slå vilken sten. Hur många sätt kan det göras på?

Sannolikhetsfördelningar I den deskriptiva statistiken visade vi hur man kan använda stapeldiagram och histogram för att visa fördelningen i ett faktiskt datamaterial. En sannolikhetsfördelning är snarlik men då den deskriptiva statistiken visar vad som har hänt visar sannolikhetsfördelningen vad som ”borde” hända i framtiden.

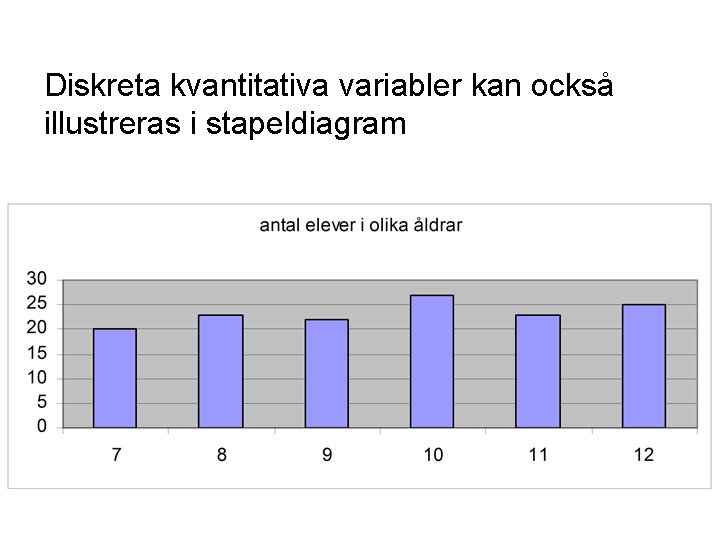
Frekvenstabeller, kvantitativ variabel Exempel Vi vill beskriva åldersstrukturen hos eleverna i en skola Ålder 7 8 9 10 11 12 Antal elever, frekvens 20 23 22 27 23 25 n = 140 Andel elever, relativ frekvens 14 16 16 19 16 18 100

Diskreta kvantitativa variabler kan också illustreras i stapeldiagram

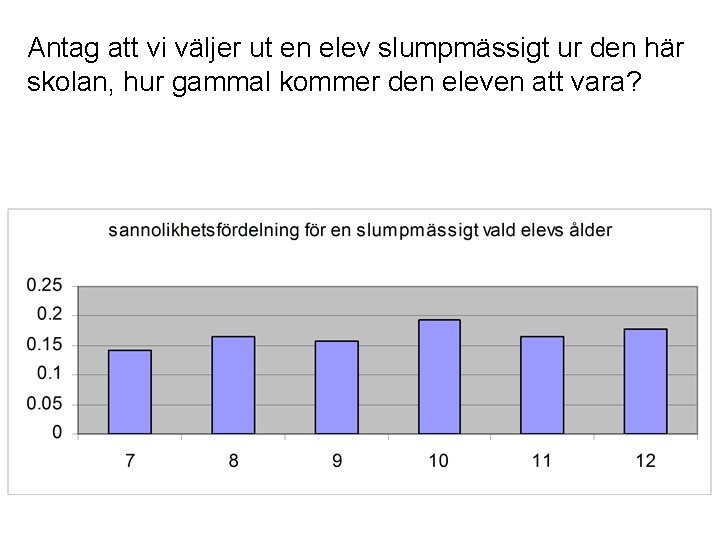
Antag att vi väljer ut en elev slumpmässigt ur den här skolan, hur gammal kommer den eleven att vara?

Egenskaper hos en sannolikhetsfördelning. Sannolikheten för ett enskilt utfall är ett tal mellan 0 och 1. Utfallen är ömsesidigt uteslutande händelser. Summan av sannolikheten för alla möjliga utfall är 1

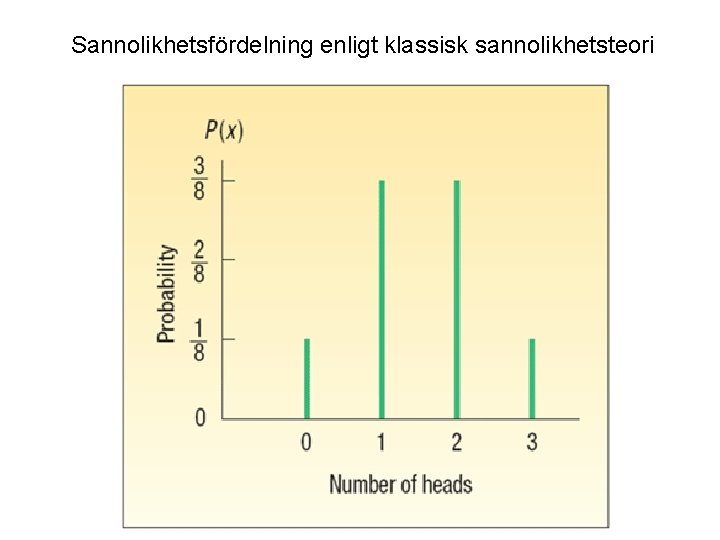
Sannolikhetsfördelning En lista över ett experiments alla utfall och deras sannolikheter Experiment: Singla slant tre gånger och räkna antalet krona, vi har fyra olika utfall: 0 1 2 3 Hur ser sannolikhetsfördelningen ut för antalet krona?

Sannolikhetsfördelning enligt klassisk sannolikhetsteori

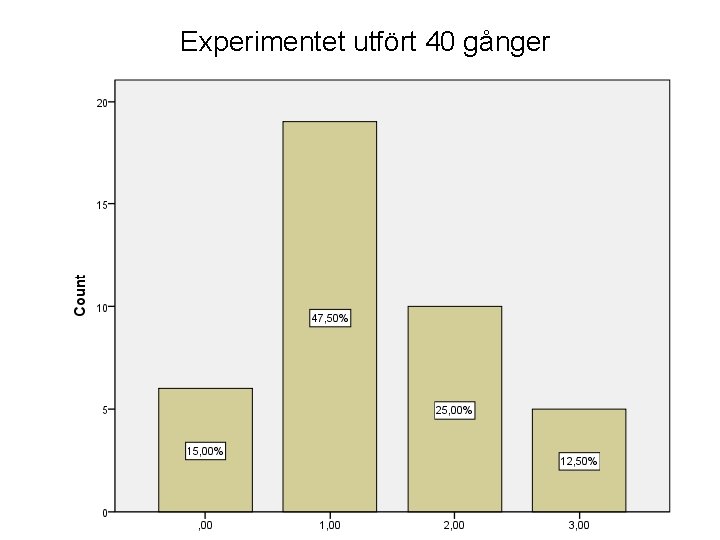
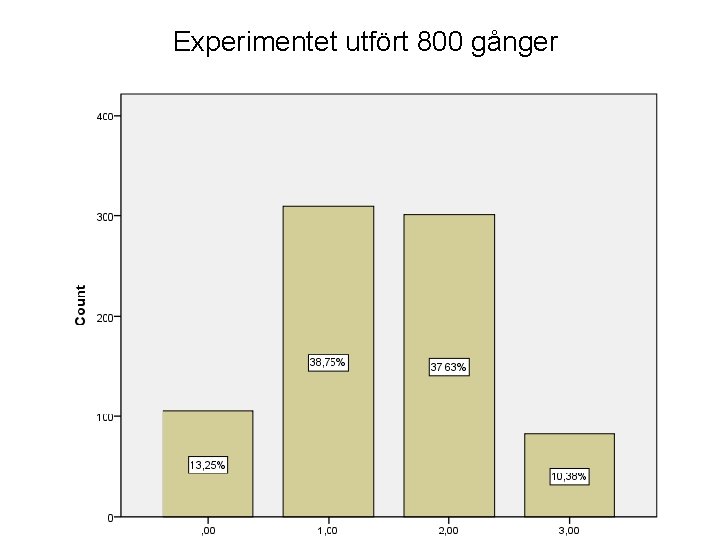
Antag att vi utför experimentet ett flertal gånger och redovisar resultatet som ett stapeldiagram över relativa frekvenserna för de olika händelserna. Vi kommer då ibland att få stapeldiagram som avviker från sannolikhetsfördelningen. Dessa är dock bara deskriptiv statistik över ett specifikt experiment, sannolikhetsfördelningen är oförändrad. Ju fler gånger vi utför experimentet desto närmare desto mindre skillnad mellan vårt experiment och den sanna sannolikhetsfördelningen. ”The law of large numbers”

Experimentet utfört 40 gånger

Experimentet utfört 800 gånger

Slumpvariabel - random variable. En kvantitet som är resultatet av ett experiment och som kan anta olika värden. Diskret slumpvariabel - discrete random variable. En slumpvariabel som enbart kan anta vissa distinkta värden. Kontinuerlig slumpvariabel - continous random variable. En slumpvariabel som kan anta alla värden inom ett intervall.

Frekvenstabeller, kvantitativ variabel Exempel Vi vill beskriva åldersstrukturen hos eleverna i en skola Ålder 7 8 9 10 11 12 Antal elever, frekvens 20 23 22 27 23 25 n = 140 Andel elever, relativ frekvens 14 16 16 19 16 18 100

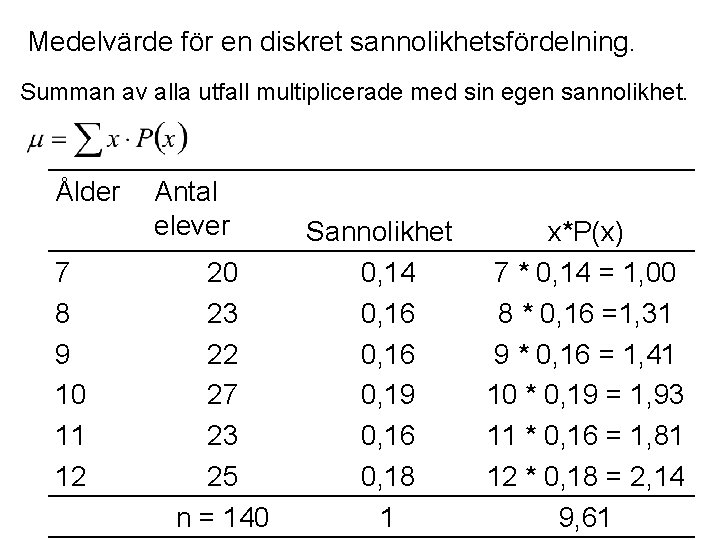
Medelvärde för en diskret sannolikhetsfördelning. Summan av alla utfall multiplicerade med sin egen sannolikhet. Ålder 7 8 9 10 11 12 Antal elever 20 23 22 27 23 25 n = 140 Sannolikhet 0, 14 0, 16 0, 19 0, 16 0, 18 1 x*P(x) 7 * 0, 14 = 1, 00 8 * 0, 16 =1, 31 9 * 0, 16 = 1, 41 10 * 0, 19 = 1, 93 11 * 0, 16 = 1, 81 12 * 0, 18 = 2, 14 9, 61

Varians för en diskret sannolikhetsfördelning. Summan av kvadrerade avvikelsen mellan varje utfall och medelvärdet multiplicerat med utfallets sannolikhet. Ålder Sannolikhet Avvikelse från μ (x – μ)2 *P(x) 7 0, 14 7 -9, 61 = - 2, 61 -2, 612 * 0, 14 = 0, 97 8 0, 16 8 -9, 61 = - 1, 61 -1, 612 * 0, 16 = 0, 42 9 0, 16 9 -9, 61 = - 0, 61 -0, 612 * 0, 16 = 0, 06 10 0, 19 10 -9, 61 = 0, 392 * 0, 19 = 0, 03 11 0, 16 11 -9, 61 = 1, 392 * 0, 16 = 0, 32 12 0, 18 12 -9, 61 = 2, 392 * 0, 18 = 1, 02 1 Standardavvikelsen 2, 82

Några specialfall av diskreta sannolikhetsföredelningar: Uniform diskret sannolikhetsfördelning. Binomial sannolikhetsfördelning Hypergeometrisk sannolikhetsfördelning Poisson fördelningen ingår ej i kursen

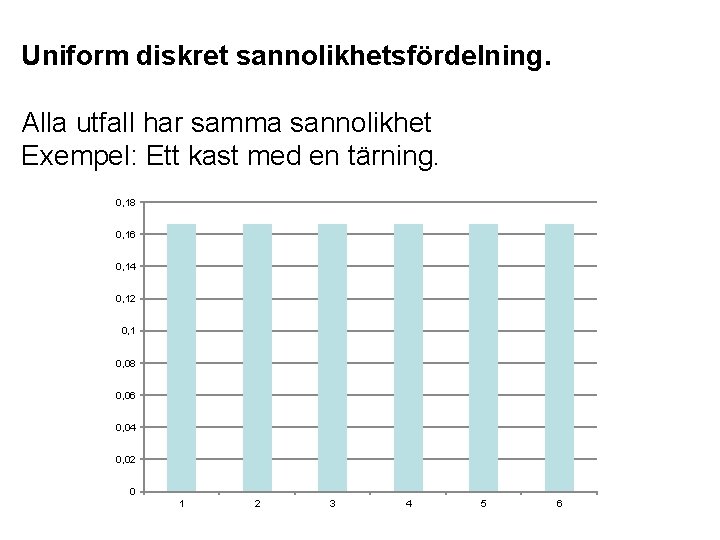
Uniform diskret sannolikhetsfördelning. Alla utfall har samma sannolikhet Exempel: Ett kast med en tärning. 0, 18 0, 16 0, 14 0, 12 0, 1 0, 08 0, 06 0, 04 0, 02 0 1 2 3 4 5 6

Binomial sannolikhetsfördelning Egenskaper: 1. Slumpvariabel som räknar antalet gånger något inträffar. 2. Varje delförsök har två utfall. 3. Sannolikheten för ja är samma i varje delförsök. 4. Delförsöken är oberoende, utfallet i ett delförsök påverkar inte sannolikheten i nästa.

Binomial sannolikhetsfördelning Antalet flickor i en 5 barnsfamilj är en binomialfördelad slumpvariabel. Varje gång föräldrarna får ytterligare ett barn kan det antingen vara en flicka eller inte en flicka. Varje försök har bara 2 utfall.

Binomial sannolikhetsfördelning Antalet flickor i en 5 barnsfamilj är en binomialfördelad slumpvariabel.

Binomial sannolikhetsfördelning Antalet flickor i en 5 barnsfamilj är en binomialfördelad slumpvariabel. Se också tabell på sid 774

Medelvärde och varians för en binomialfördelning

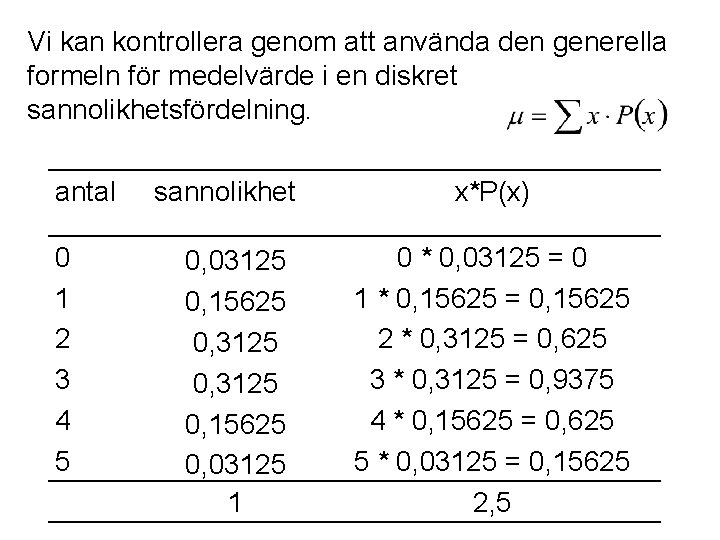
Vi kan kontrollera genom att använda den generella formeln för medelvärde i en diskret sannolikhetsfördelning. antal 0 1 2 3 4 5 sannolikhet 0, 03125 0, 15625 0, 03125 1 x*P(x) 0 * 0, 03125 = 0 1 * 0, 15625 = 0, 15625 2 * 0, 3125 = 0, 625 3 * 0, 3125 = 0, 9375 4 * 0, 15625 = 0, 625 5 * 0, 03125 = 0, 15625 2, 5

Hypergeometrisk sannolikhetsfördelning En hypergeometrisk sannolikhetsfördelning uppkommer när vi tar ett urval ur en population och räknar antalet som har en viss egenskap. (Sannolikheten ändras vid varje dragning för antalet kvarvarande individer med respektive utan egenskapen ändras. ) (Om vi lägger tillbaka objekten igen mellan varje dragning får vi en binomialfördelning eftersom sannolikheterna då är oförändrade. )

Hypergeometrisk sannolikhetsfördelning Sannolikheten vid nästa dragning ändras. Exempel: Curlingklubben ska lotta fram ett lag med både killar och tjejer. Antalet tjejer i ett slumpvis valt lag är en hypergeometriskt fördelad slumpvariabel N = populationstorleken S = antalet ja i hela populationen x = antalet ja i urvalet n = storleken på urvalet n. Cx = Alla möjliga kombinationer av x element ur en population på n element.

Hypergeometrisk sannolikhetsfördelning Sannolikheten vid nästa dragning ändras. Exempel: Curlingklubben ska lotta fram ett lag med både killar och tjejer. Antalet tjejer i ett slumpvis valt lag är en hypergeometriskt fördelad slumpvariabel

Hypergeometrisk sannolikhetsfördelning Sannolikheten vid nästa dragning ändras. Exempel: Curlingklubben ska lotta fram ett lag med både killar och tjejer. Antalet tjejer i ett slumpvis valt lag är en hypergeometriskt fördelad slumpvariabel

Hypergeometrisk sannolikhetsfördelning Sannolikheten vid nästa dragning ändras. Exempel: Curlingklubben ska lotta fram ett lag med både killar och tjejer. Antalet tjejer i ett slumpvis valt lag är en hypergeometriskt fördelad slumpvariabel

Hypergeometrisk sannolikhetsfördelning Sannolikheten vid nästa dragning ändras. Exempel: Curlingklubben ska lotta fram ett lag med både killar och tjejer. Antalet tjejer i ett slumpvis valt lag är en hypergeometriskt fördelad slumpvariabel

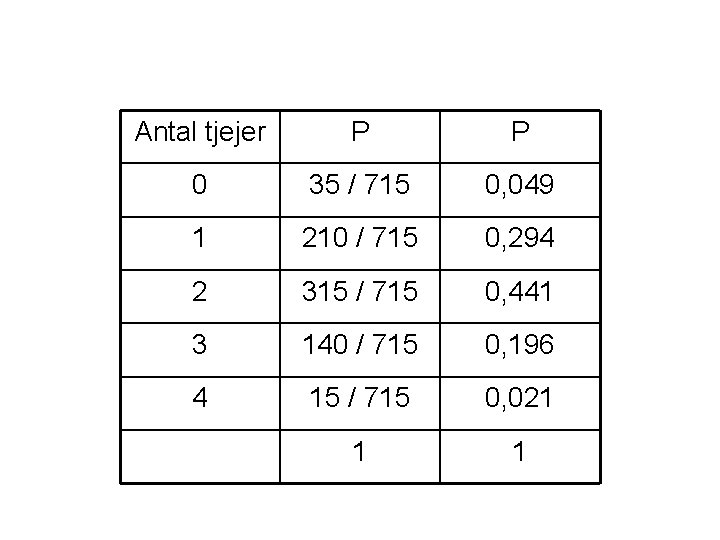
Hypergeometrisk sannolikhetsfördelning Sannolikheten vid nästa dragning ändras. Exempel: Curlingklubben ska lotta fram ett lag med både killar och tjejer. Antalet tjejer i ett slumpvis valt lag är en hypergeometriskt fördelad slumpvariabel

Antal tjejer P P 0 35 / 715 0, 049 1 210 / 715 0, 294 2 315 / 715 0, 441 3 140 / 715 0, 196 4 15 / 715 0, 021 1 1

Slumpvariabel: Antal röda kulor. Exempel 1 I en urna finns 5 röda och 10 svarta kulor. Du drar 4 gånger slumpmässigt 1 kula ur urnan, mellan varje dragning lägger du tillbaka den kula du drog. Exempel 2 Samma som ovan men utan återläggning.

Du slår tre slag med en tärning. Slumpvariabel: antal sexor

Om du har slått två sexor i rad, hur stor är då sannolikheten att du får en 6 i tredje kastet?

Kontinuerliga sannolikhetsfördelningar 1. Uniform sannolikhetsfördelning 2. Normalfördelning 3. Exponentialfördelning

Uniform sannolikhetsfördelning Om x kan anta värden som är större än eller lika med a men mindre än eller lika med b och alla utfall är lika sannolika då är x en slumpvariabel med en uniform sannolikhetsfördelning. Diskret uniform fördelning Ett kast med en tärning. Alla 6 heltal mellan 1 och 6 är lika sannolika. Kontinuerlig uniform fördelning Skillnaden mot den diskreta uniforma fördelningen är att den kan anta alla värden i intervallet, (även decimaltal).

Kontinuerlig uniform fördelning Exempel: En buss avgår var 20 minut. Om alla bussar går i tid är den maximala väntetiden 20 minuter. Väntetiden är en slumpvariabel med gränserna 0 och 20. Antag att du inte vet när bussen går. Förmodligen är då alla tider du väljer att gå till busshållplatsen lika sannolika. I så fall är väntetiden uniformt fördelad mellan 0 och 20 minuter.

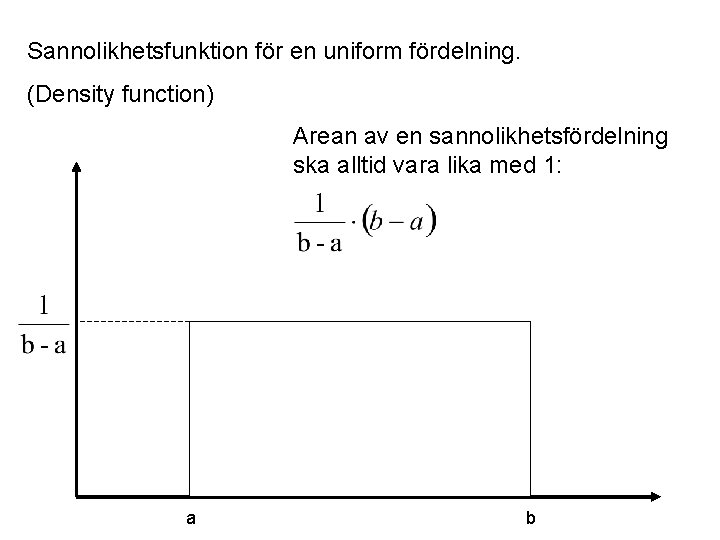
Sannolikhetsfunktion för en uniform fördelning. (Density function) Arean av en sannolikhetsfördelning ska alltid vara lika med 1: a b

Att räkna på uniforma sannolikhetsfördelningar I kontinuerliga sannolikhetsfördelningar är sannolikheten för ett enskilt tal lika med noll. Vi kan bara räkna sannolikheten för ett intervall. (Sannolikheten att utfallet blir 2 är extremt liten eftersom det förmodligen inte blir 2 om vi specificerar tillräckligt många decimaler. 2, 0000000000000000000001 är ju inte lika med 2. )

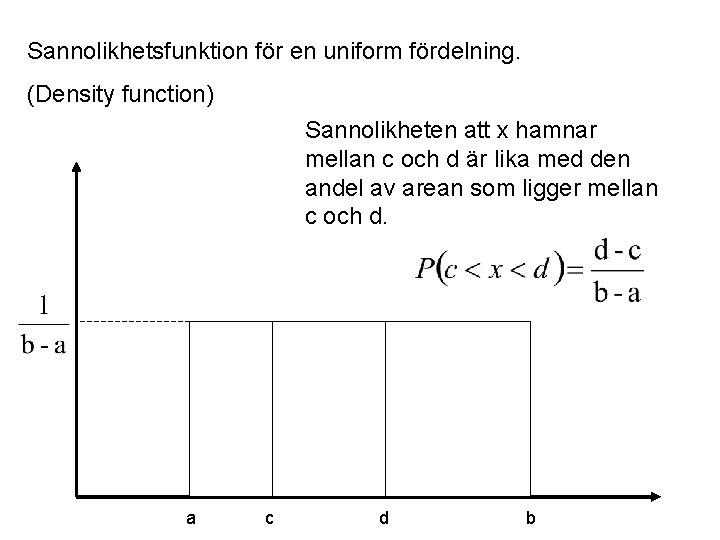
Sannolikhetsfunktion för en uniform fördelning. (Density function) Sannolikheten att x hamnar mellan c och d är lika med den andel av arean som ligger mellan c och d. a c d b

Sannolikhetsfunktion för en uniform fördelning. (Density function) Exempel: x är uniformt fördelad med största värde 10 och minsta värde 1. Vad är sannolikheten att få ett värde mellan 3 och 5?

Kontinuerliga sannolikhetsfördelningar som inte är uniforma Exempel: En buss avgår var 20 minut. Om alla bussar går i tid är den maximala väntetiden 20 minuter. Väntetiden är en slumpvariabel med gränserna 0 och 20. Antag att du vet när bussen går. Förmodligen försöker du då komma till busshållplatsen ca 3 minuter innan för att inte missa bussen, men inte heller behöva vänta för länge. Det innebär att alla väntetider inte har samma sannolikhet. Vi har inte en uniform fördelning.

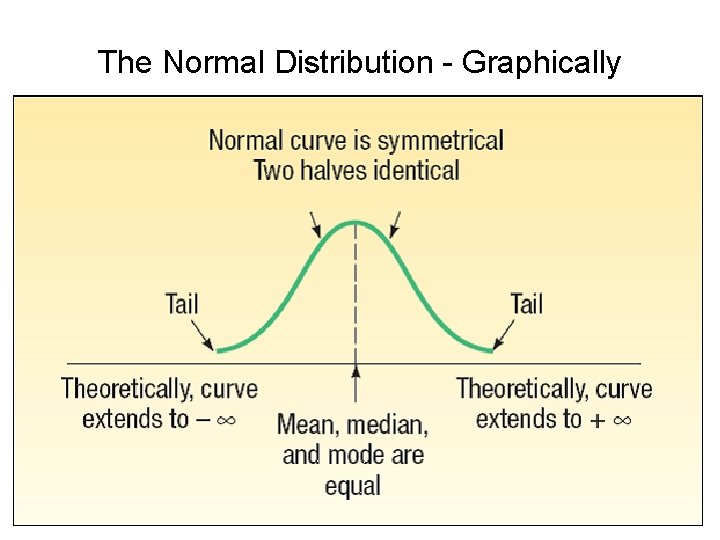
Egenskaper hos en normalfördelning Lite svårare att räkna på men vanligare i verkligheten. En normalfördelning specificeras medelvärde och standardavvikelse. En normalfördelning är klockformad. En normalfördelning är symmetrisk, båda sidor om medelvärdet är varandras spegelbilder. En normalfördelning innehåller oändligt stora och oändligt små tal men sannolikheten att de realiseras blir allt mindre ju längre från medelvärdet de är. Totala arean under kurvan är lika med 1, arean under medelvärdet är lika med 0, 5 (och arean över medelvärdet är också lika med 0, 5)

The Normal Distribution - Graphically

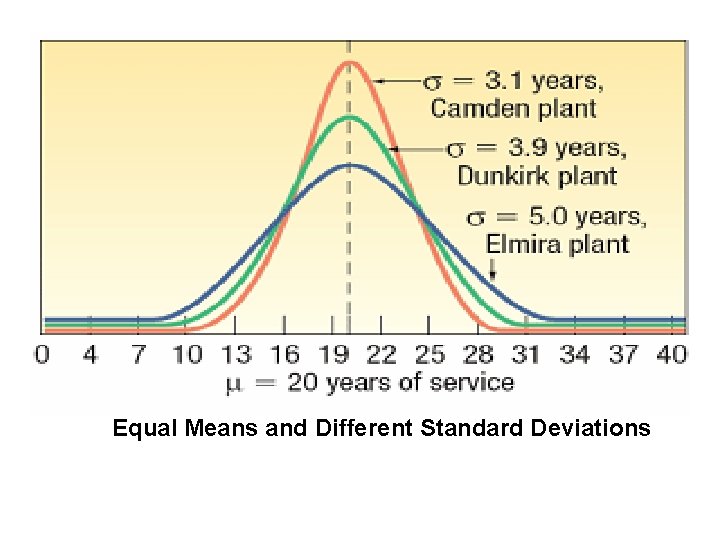
Equal Means and Different Standard Deviations

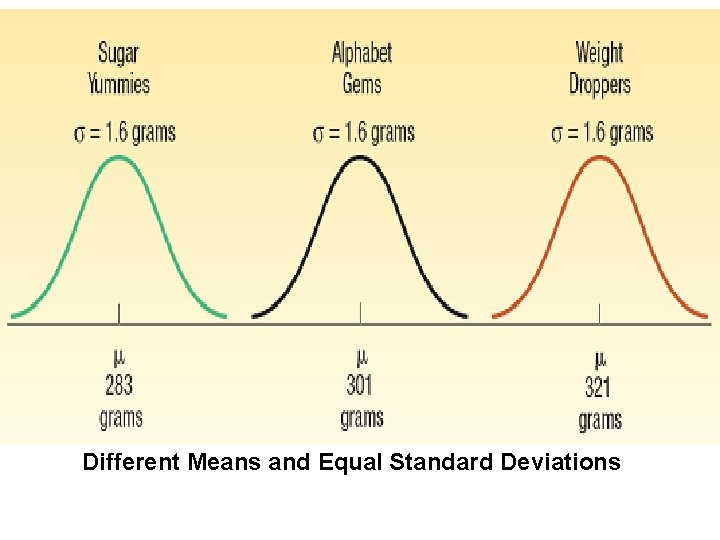
Different Means and Equal Standard Deviations

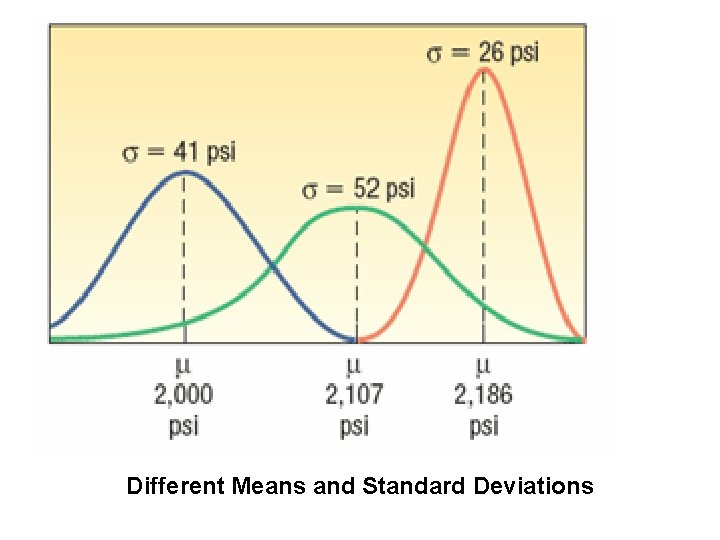
Different Means and Standard Deviations

Normalfördelningens sannolikhetsfunktion Normalfördelningar definieras utifrån medelvärde och standardavvikelse. Normalfördelning medelvärde 3 och standardavvikelse 2

Den standardiserade normalfördelningen har medelvärde 0 och standardavvikelse 1. Det finns tabeller över sannolikheter för den standardiserade normalfördelningen. Tabellen i boken anger sannolikheten att dra ett tal som ligger i intervallet mellan 0 och ett specificerat tal, z. Exempel: Vad är sannolikheten att ur en standardiserad normalfördelning dra ett tal mellan 0 och 2?

Den standardiserade normalfördelningen har medelvärde 0 och standardavvikelse 1. Det finns tabeller över sannolikheter för den standardiserade normalfördelningen. Tabellen i boken anger sannolikheten att dra ett tal som ligger i intervallet mellan 0 och ett specificerat tal, z. Exempel: Vad är sannolikheten att ur en standardiserad normalfördelning dra ett tal mellan 0 och 2?

Vad är sannolikheten att ur den standardiserade normalfördelningen dra ett tal som är mindre än 2? Ett annat exempel: Vad är sannolikheten att ur den standardiserade normalfördelningen dra ett tal som är mindre än minus 1. 5

Vad är sannolikheten att ur den standardiserade normalfördelningen dra ett tal som är mindre än 2? Ett annat exempel: Vad är sannolikheten att ur den standardiserade normalfördelningen dra ett tal som är mindre än minus 1.

Alla normalfördelningar kan konverteras till den standardiserade normalfördelningen.

Alla normalfördelningar kan konverteras till den standardiserade normalfördelningen. 14 % av svenska män är längre än 187. 4 cm

Vad är sannolikheten att från en godtycklig normalfördelning få ett tal som är mer än en standardavvikelse större än medelvärdet

Vad är sannolikheten att från en godtycklig normalfördelning få ett tal som är mer än en standardavvikelse större än medelvärdet Sannolikheten att få ett tal som är mer än en standardavvikelse större än medelvärdet är ca 16 % i alla normalfördelningar. Vad är sannolikheten att dra ett tal som avviker mer än en normalfördelning från medelvärdet? 68, 3 % av alla observationer är mindre än en standardavvikelse från medelvärdet.

The empirical rule 68, 3% 95, 4%

The empirical rule 68, 3% 95, 4% 99, 7%

The Empirical Rule

The empirical rule 68, 3% 95, 4% 99, 7% 95 % 99 %

Ett annat exempel Hur stor andel av svenska män har en kroppslängd i intervallet 182 - 185 cm?

Ett annat exempel Hur stor andel av svenska män har en kroppslängd i intervallet 182 - 185 cm?

Ett annat exempel Hur stor andel av svenska män har en kroppslängd i intervallet 182 - 185 cm? 0, 7486 - 0, 5675 = 0, 1811

Exponentialfördelningen Används i första hand för att beskriva tidsperioder. Arbetslöshetstider Sjukskrivningstider

0