INFR NATIONELLA PROVET MATEMATIK 2 b Np Ma

INFÖR NATIONELLA PROVET MATEMATIK 2 b

Np. Ma 2 b Muntlig del vt 2012

Np. Ma 2 b Muntlig del vt 2012
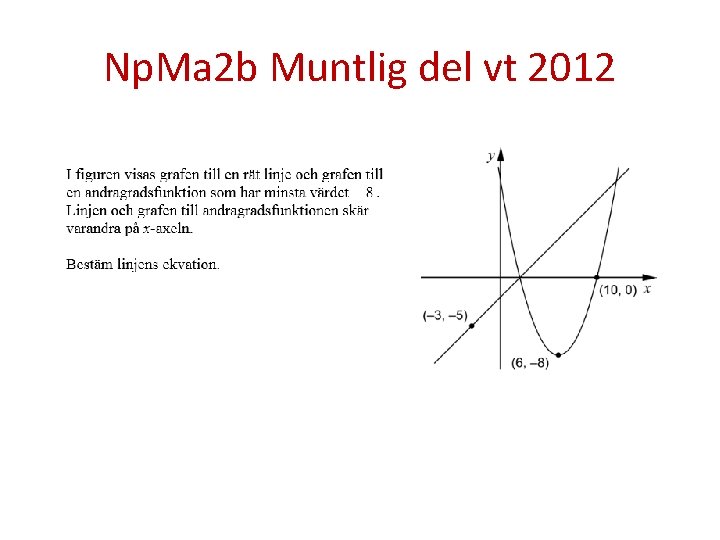
Np. Ma 2 b Muntlig del vt 2012

Np. Ma 2 b Muntlig del vt 2012

MATMAT 02 b – UPPGIFT 0 Förenkla så långt som möjligt

MATMAT 02 b – UPPGIFT 1 N KO O TR R E LL T I D A V S T ! R A
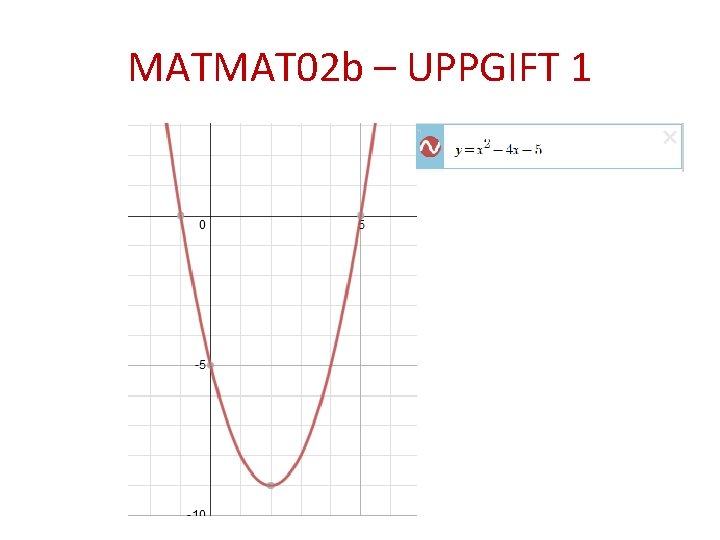
MATMAT 02 b – UPPGIFT 1

MATMAT 02 b – UPPGIFT 2

MATMAT 02 b – UPPGIFT 2 N KO O TR R E LL T I D A V S T ! R A

MATMAT 02 b – UPPGIFT 3

MATMAT 02 b – UPPGIFT 3

MATMAT 02 b – UPPGIFT 4

MATMAT 02 b – UPPGIFT 4

MATMAT 02 b – UPPGIFT 4

MATMAT 02 b – UPPGIFT 5 Andra kvadreringsregeln:

MATMAT 02 b – UPPGIFT 6

MATMAT 02 b – UPPGIFT 7
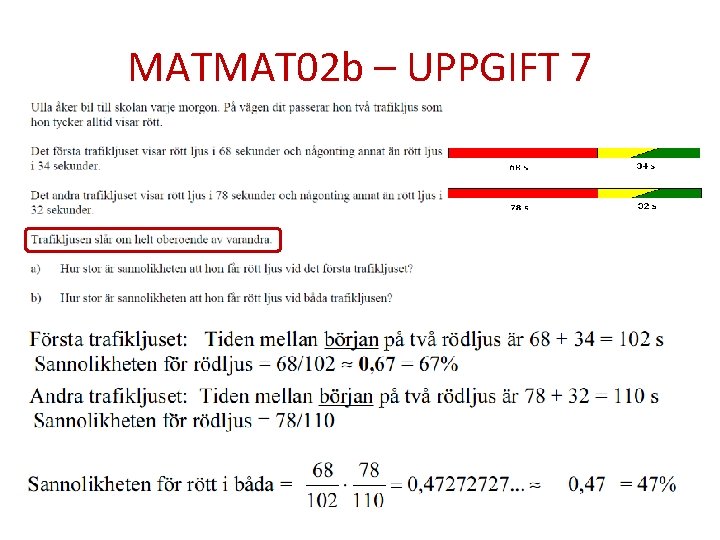
MATMAT 02 b – UPPGIFT 7

MATMAT 02 b – UPPGIFT 8

MATMAT 02 b – UPPGIFT 8 (Transversalsatsen)

MATMAT 02 b – UPPGIFT 8

MATMAT 02 b – UPPGIFT 9 RÄTT! ! Vid multiplikation och division med negativt tal (ex. -2) måste man vända på olikhetstecknet
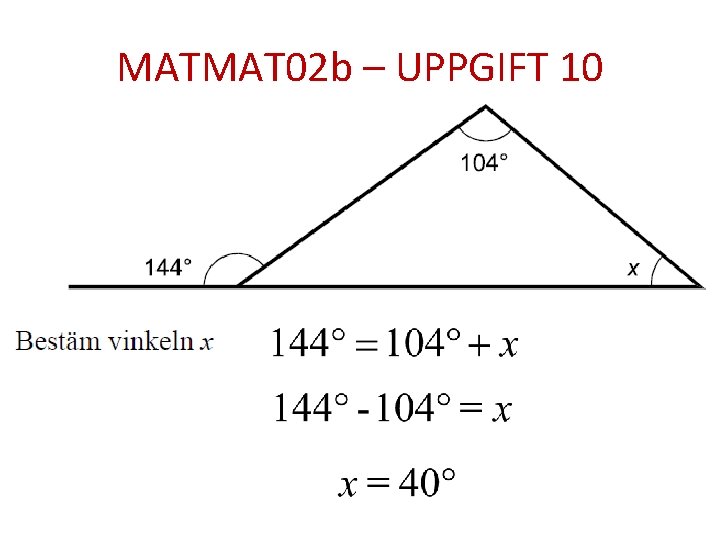
MATMAT 02 b – UPPGIFT 10
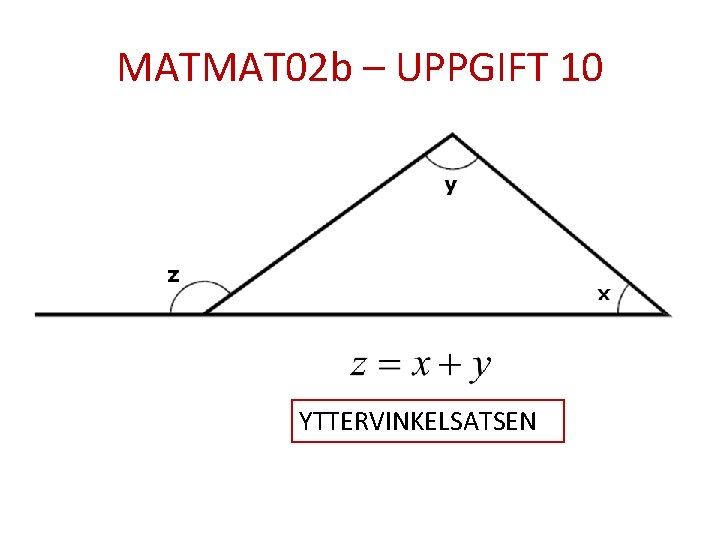
MATMAT 02 b – UPPGIFT 10 YTTERVINKELSATSEN
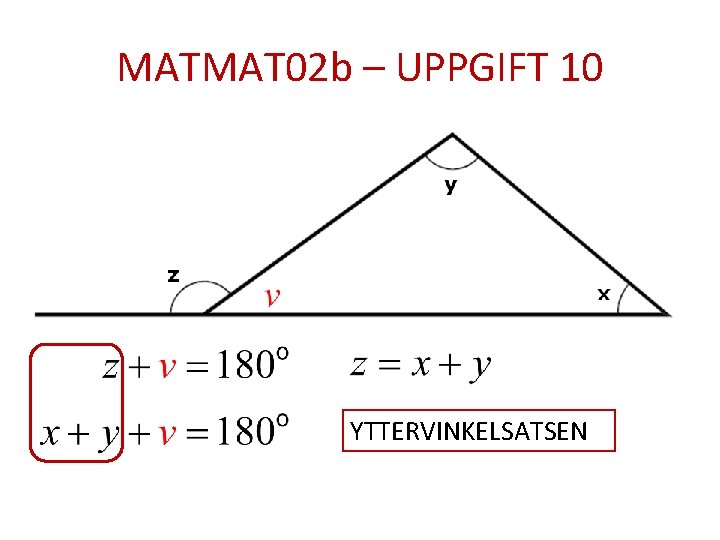
MATMAT 02 b – UPPGIFT 10 YTTERVINKELSATSEN
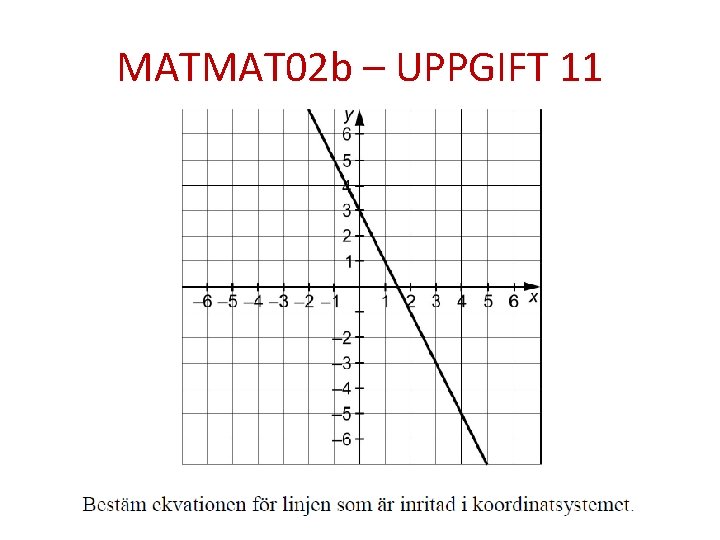
MATMAT 02 b – UPPGIFT 11

MATMAT 02 b – UPPGIFT 11 m=3 k = -2 y = -2 x + 3 Hur ser man att k = -2 ?

MATMAT 02 b – UPPGIFT 12 -4

MATMAT 02 b – UPPGIFT 12
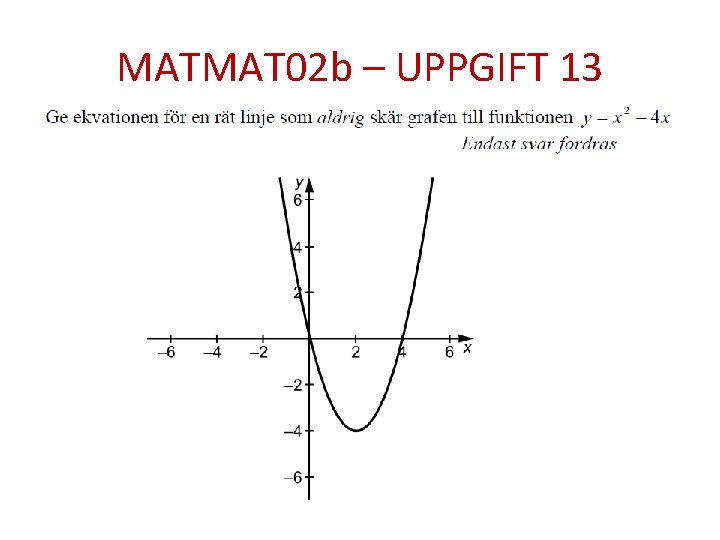
MATMAT 02 b – UPPGIFT 13
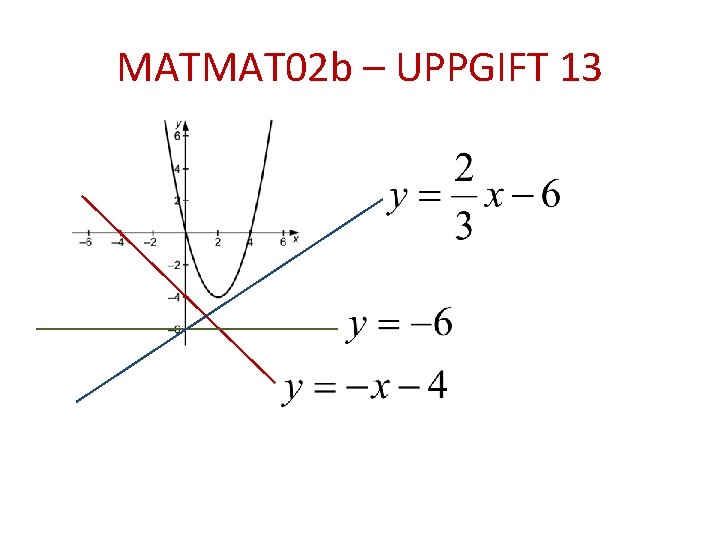
MATMAT 02 b – UPPGIFT 13

MATMAT 02 b – UPPGIFT 14
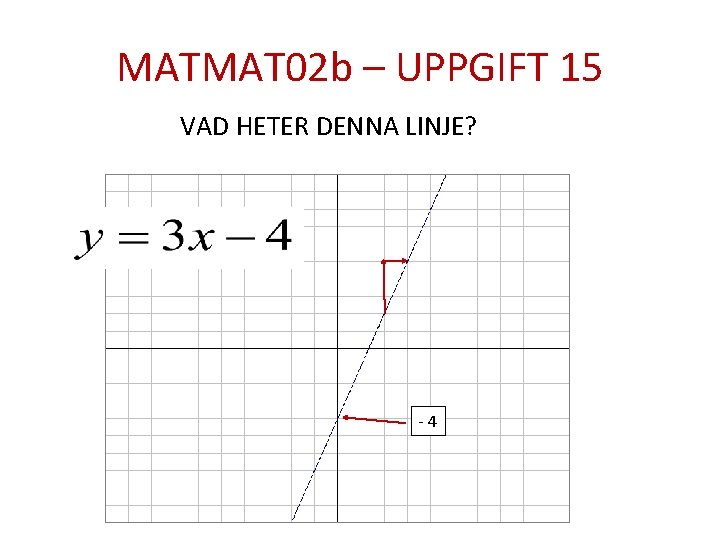
MATMAT 02 b – UPPGIFT 15 VAD HETER DENNA LINJE? -4
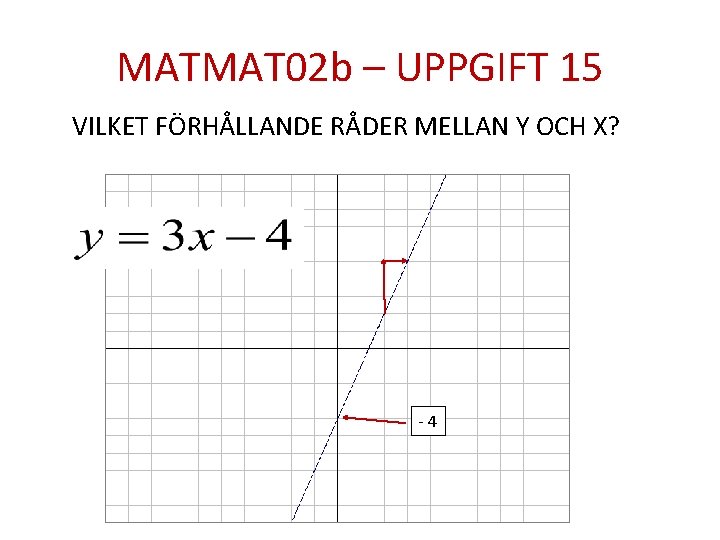
MATMAT 02 b – UPPGIFT 15 VILKET FÖRHÅLLANDE RÅDER MELLAN Y OCH X? -4
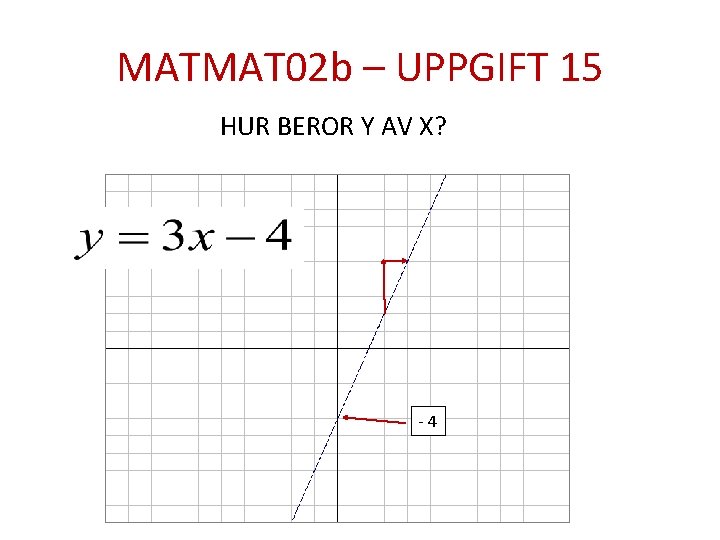
MATMAT 02 b – UPPGIFT 15 HUR BEROR Y AV X? -4
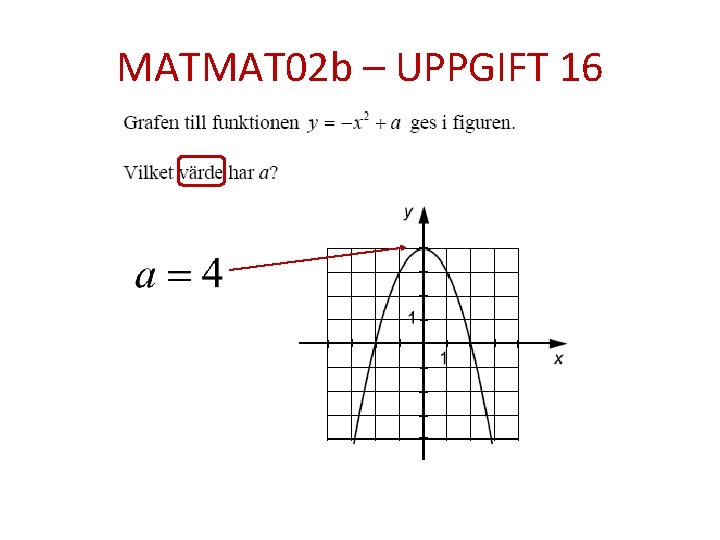
MATMAT 02 b – UPPGIFT 16
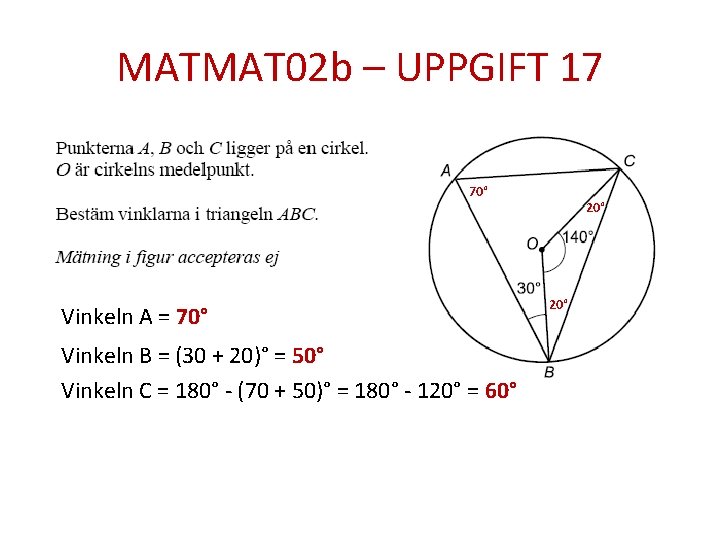
MATMAT 02 b – UPPGIFT 17 70° Vinkeln A = 70° Vinkeln B = (30 + 20)° = 50° Vinkeln C = 180° - (70 + 50)° = 180° - 120° = 60° 20°
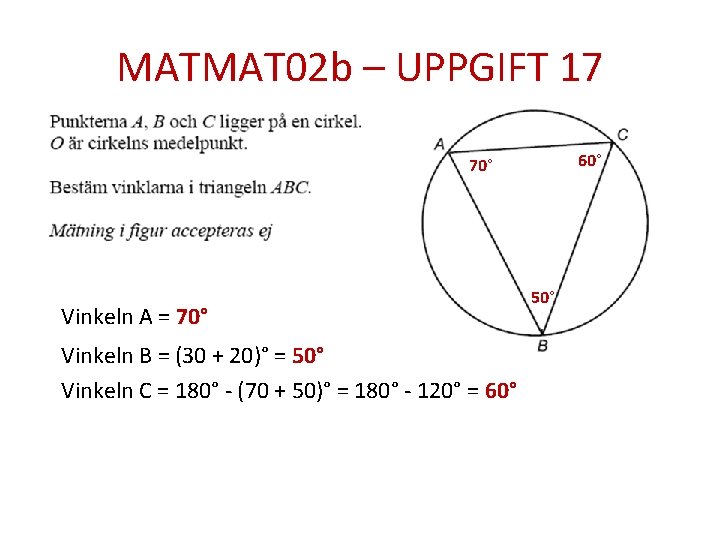
MATMAT 02 b – UPPGIFT 17 60° 70° Vinkeln A = 70° Vinkeln B = (30 + 20)° = 50° Vinkeln C = 180° - (70 + 50)° = 180° - 120° = 60° 50°
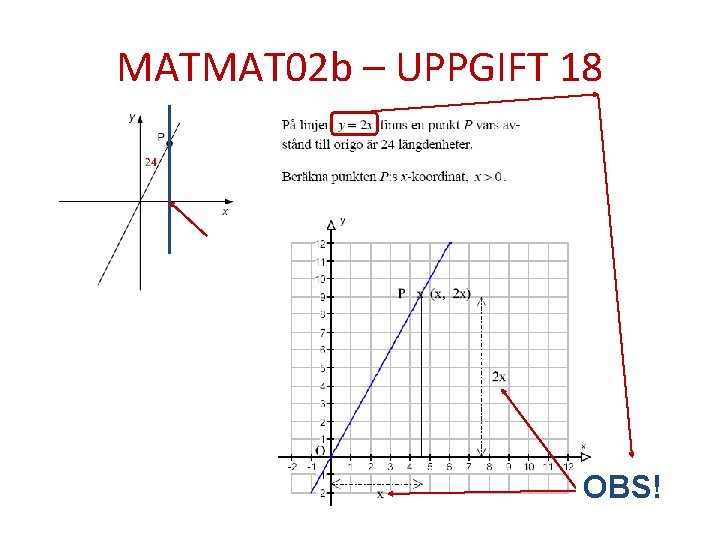
MATMAT 02 b – UPPGIFT 18 OBS!
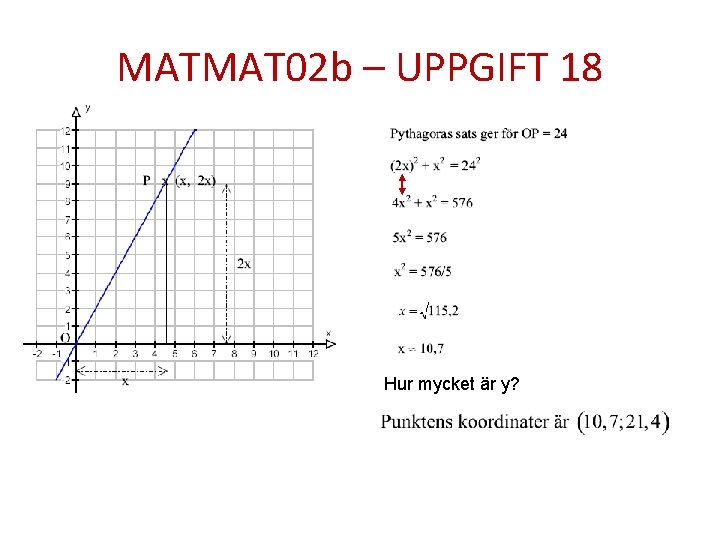
MATMAT 02 b – UPPGIFT 18 Hur mycket är y?

MATMAT 02 b – UPPGIFT 19

MATMAT 02 b – UPPGIFT 20

MATMAT 02 b – UPPGIFT 21
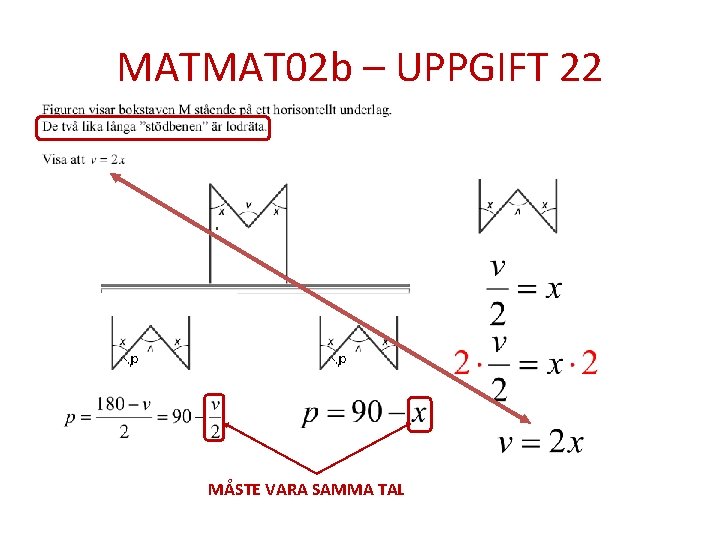
MATMAT 02 b – UPPGIFT 22 MÅSTE VARA SAMMA TAL
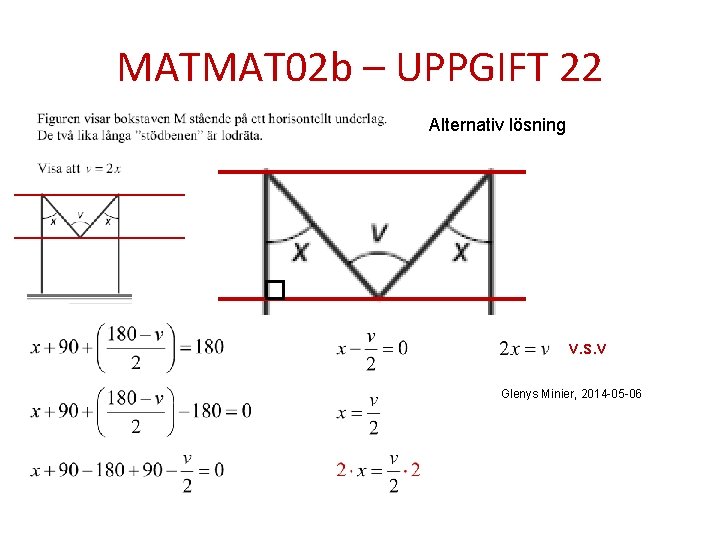
MATMAT 02 b – UPPGIFT 22 Alternativ lösning v. s. v Glenys Minier, 2014 -05 -06

MATMAT 02 b – UPPGIFT 23 KVADRERINGSREGLERNA
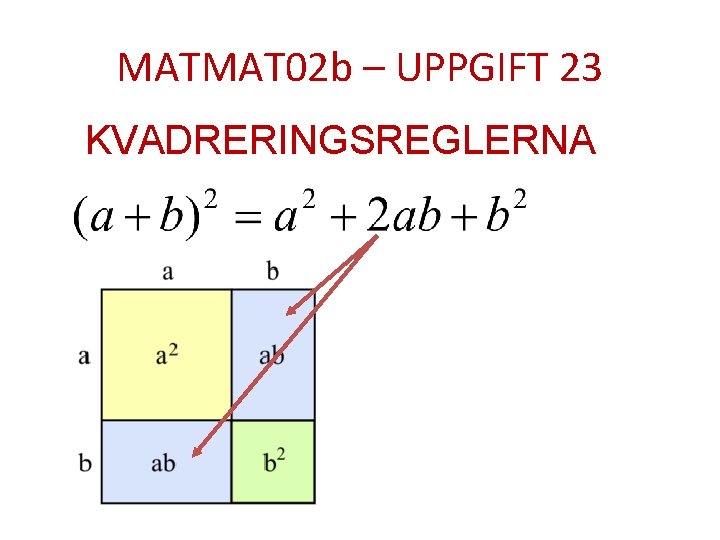
MATMAT 02 b – UPPGIFT 23 KVADRERINGSREGLERNA

MATMAT 02 b – UPPGIFT 24 KONJUGATREGELN

MATMAT 02 b – UPPGIFT 25

MATMAT 02 b – UPPGIFT 25 ETTA - ETTA TVÅA - ETTA - TVÅA jämför

MATMAT 02 b – UPPGIFT 26 (24 – x) En tråd som är 48 cm böjs till en rektangel. a) Den ena sidan är x cm. Skriv ett uttryck för den andra sidan. • Hela omkretsen är 48 cm. • Halva omkretsen är 24 cm. • Om ena sidan är x cm, så är den andra sidan… • … (24 – x) cm

MATMAT 02 b – UPPGIFT 26 (24 – x) En tråd som är 48 cm böjs till en rektangel. b) Skriv ett uttryck för arean y cm². Sidan × sidan

MATMAT 02 b – UPPGIFT 26 (24 – x) En tråd som är 48 cm böjs till en rektangel. c) För vilka värden på x är y = 0? ”Nollproduktmetoden” d) För vilket värde på x är y störst?

MATMAT 02 b – UPPGIFT 26 (24 – x) En tråd som är 48 cm böjs till en rektangel. e) Vilken är den största arean? Största arean är 144 cm²

MATMAT 02 b – UPPGIFT 26 (24 – x) En tråd som är 48 cm böjs till en rektangel. f) Vilka värden på x är möjliga?
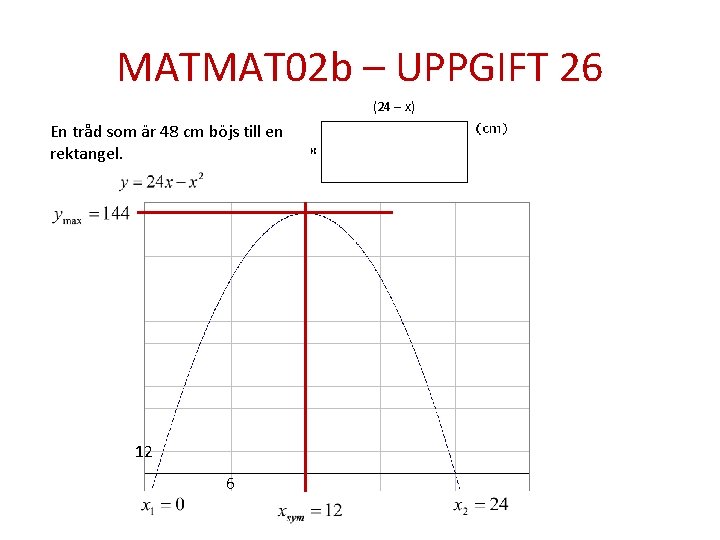
MATMAT 02 b – UPPGIFT 26 (24 – x) En tråd som är 48 cm böjs till en rektangel. 12 6

MATMAT 02 b – UPPGIFT 27 VAD HETER DENNA LINJE?

MATMAT 02 b – UPPGIFT 28 VAD HETER DENNA LINJE?

EXPONENTIALFUNKTIONER C är ”startvärde” a är förändringsfaktor x kan exempelvis vara tid i år Bok 3 bc, sidan 132

EXPONENTIALFUNKTIONER C är ”startvärde” a är förändringsfaktor x kan exempelvis vara tid i år Fråga: En stad har folkmängden 50 000 invånare. Folkmängden förväntas öka med 2% varje år. Hur många bor det i staden efter 10 år? Lösning: OBS! Vi sätter folkmängden efter 10 år till y och får då: Svar: Om 10 år är folkmängden 61 000.

EXPONENTIALFUNKTIONER C är ”startvärde” a är förändringsfaktor x kan exempelvis vara tid i år Fråga: En stad har folkmängden 50 000 invånare. Folkmängden förväntas minska med 2% varje år. Hur många bor det i staden efter 10 år? Lösning: OBS! Vi sätter folkmängden efter 10 år till y och får då: Svar: Om 10 år är folkmängden c: a 41 000.
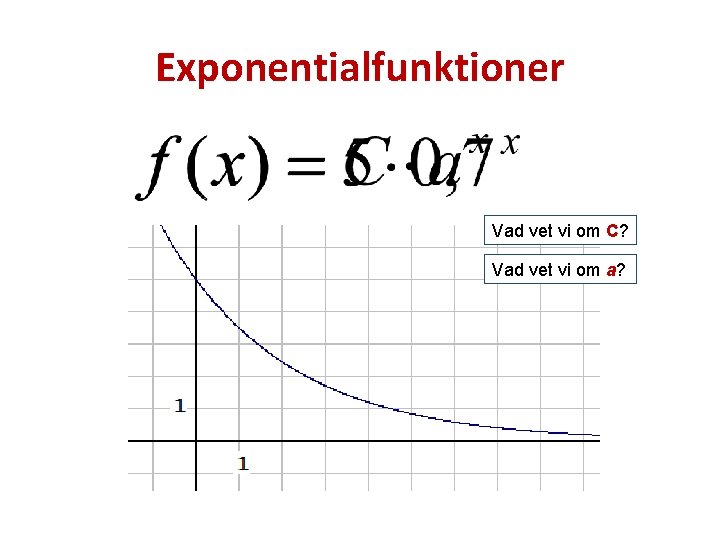
Exponentialfunktioner Vad vet vi om C? Vad vet vi om a?
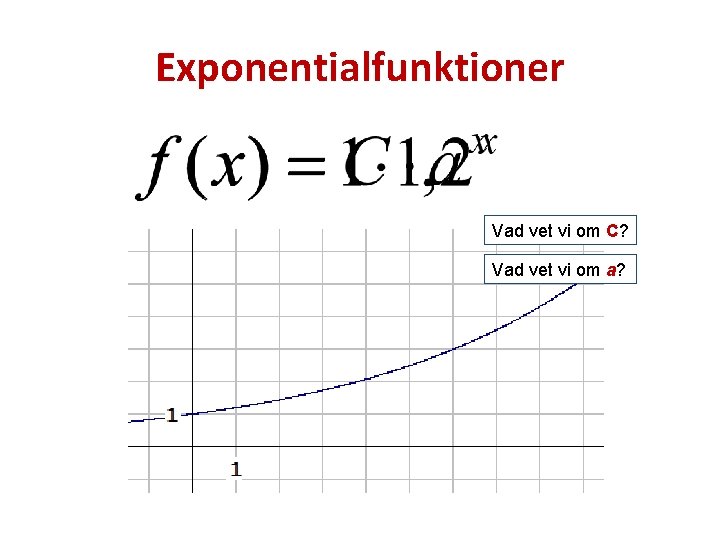
Exponentialfunktioner Vad vet vi om C? Vad vet vi om a?
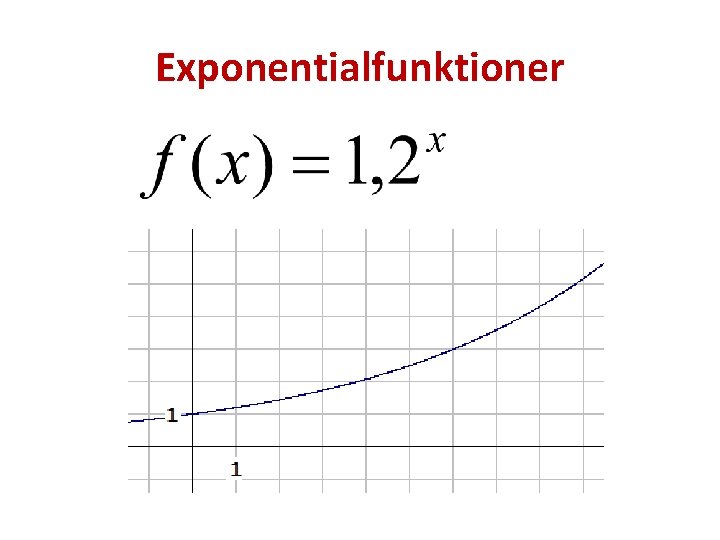
Exponentialfunktioner
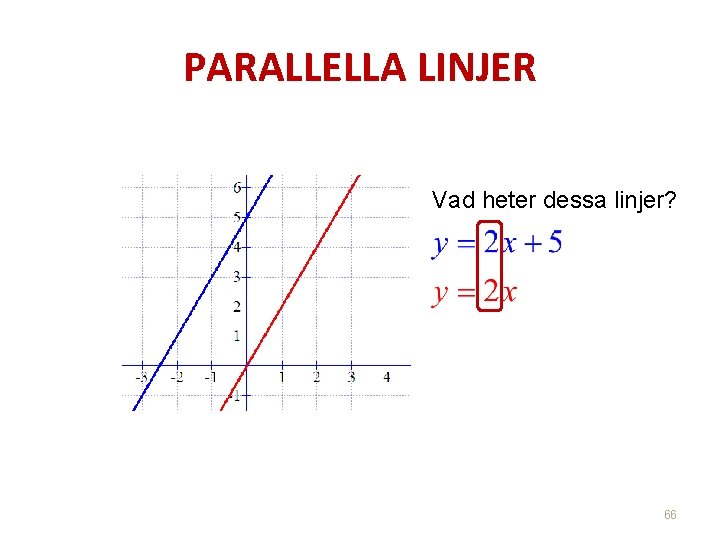
PARALLELLA LINJER Vad heter dessa linjer? 66
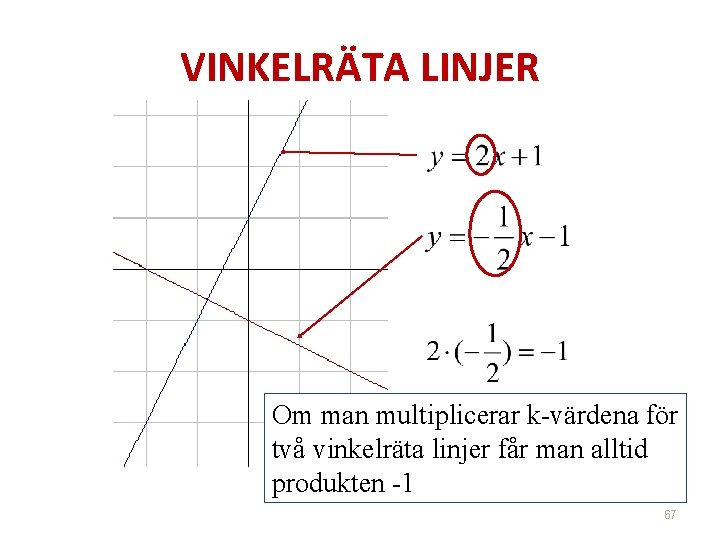
VINKELRÄTA LINJER Om man multiplicerar k-värdena för två vinkelräta linjer får man alltid produkten -1 67
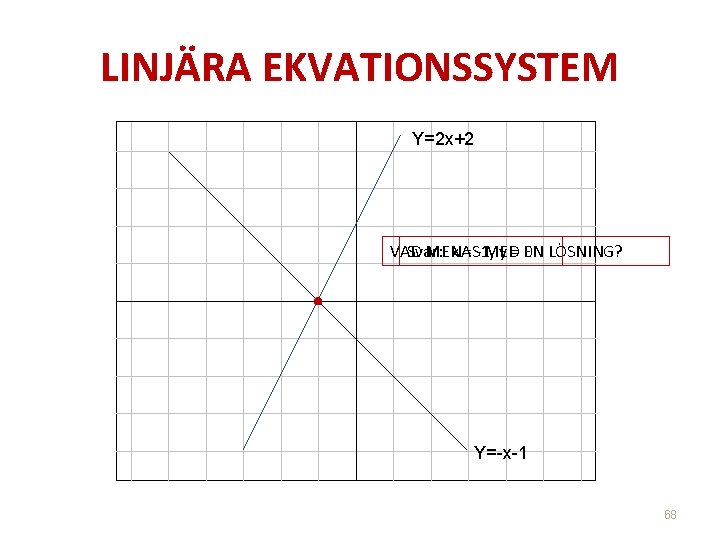
LINJÄRA EKVATIONSSYSTEM Y=2 x+2 VAD Svar: MENAS x = -1, MED y = EN 0 LÖSNING? • Y=-x-1 68

LINJÄRA EKVATIONSSYSTEM Y=2 x+2 • Y=-x-1 69

LINJÄRA EKVATIONSSYSTEM Om lösningen stämmer i båda ekvationerna så är lösningen exakt. Vi testar om lösningen är exakt: Första ekvationen Andra ekvationen Det stämmer! Hurra! 70

LINJÄRA EKVATIONSSYSTEM 71

LINJÄRA EKVATIONSSYSTEM 72

LINJÄRA EKVATIONSSYSTEM 73

Logaritmer

Logaritmer ”x är 10 -logaritmen för 7” ”x är 8 -logaritmen för 5”

Logaritmer Enligt räknaren…
![Logaritmer (1) lg(3× 4) = 1, 07918124605 --- lg(3)+lg(4) = 1, 07918124605 [test] (2) Logaritmer (1) lg(3× 4) = 1, 07918124605 --- lg(3)+lg(4) = 1, 07918124605 [test] (2)](http://slidetodoc.com/presentation_image_h2/68055f93673d132922c552d2b2ec58e0/image-77.jpg)
Logaritmer (1) lg(3× 4) = 1, 07918124605 --- lg(3)+lg(4) = 1, 07918124605 [test] (2) lg(4/3) = 0, 124938736608 --- lg(4)-lg(3) = 0, 124938736608 [test] (3) lg(3^4) = 1, 90848501888 --- 4×lg(3) = 1, 90848501888 [test]

Logaritmlagar Exempel: TESTA!

Logaritmlagar Exempel: TESTA!

Logaritmlagar Exempel: TESTA!

Logaritmer med olika baser 4 är 3 -logaritmen för 81 4 är den exponent till 3 som ger 81 4 är vad 3 skall upphöjas till för att ge svaret 81
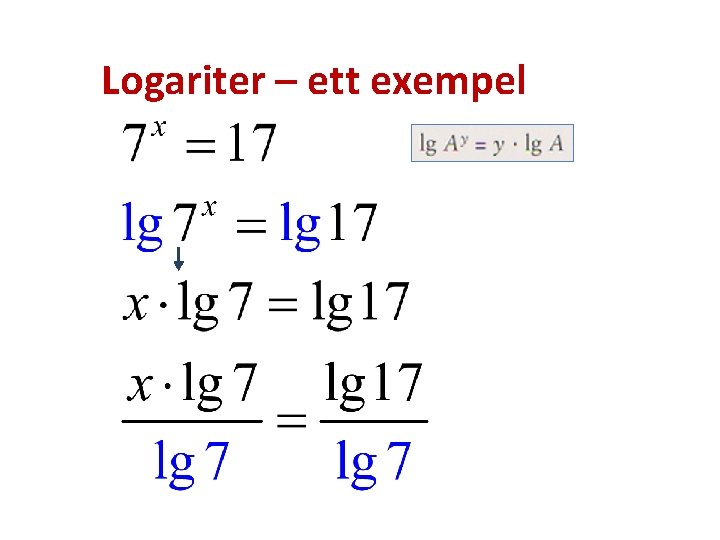
Logariter – ett exempel

Logaritmer – ett exempel På räknaren: lg(17)/lg(7) = 1, 45598364109

Logaritmer – ett exempel

Negativ exponent Youtube - Negativ exponent

Negativ exponent

Typvärde (kallas även modalvärde) i ett statistiskt datamaterial det värde som förekommer flest gånger.

Medelvärde Ett medelvärde är ett värde som används för att representera ett genomsnitt för en mängd värden. På räknaren slår man (2+5+8+9+4+7+8)/7 = 6, 14285714286…

MEDIAN Medianen är det tal i en mängd som storleksmässigt ligger i mitten. Av talen 1, 7, 9, 10 och 17 är 9 medianen (medan 8, 8 är medelvärdet). För mängder med ett jämnt antal definieras medianen som medelvärdet av de två tal som ligger i mitten.
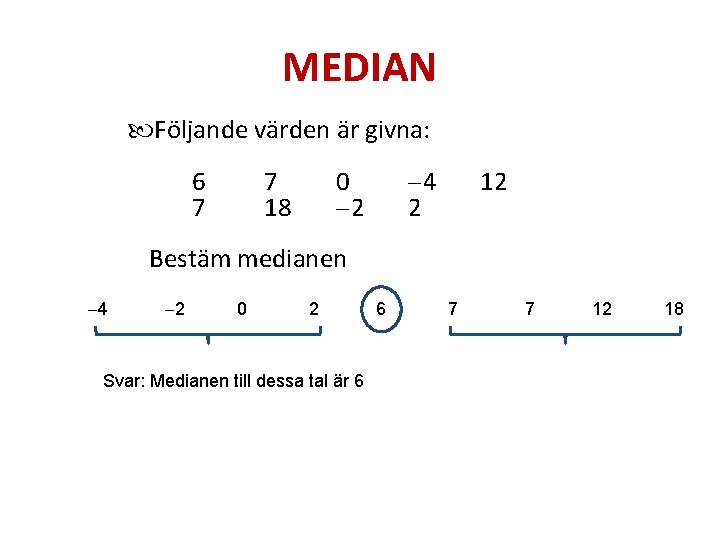
MEDIAN Följande värden är givna: 6 7 7 18 4 2 0 2 12 Bestäm medianen 4 2 0 2 Svar: Medianen till dessa tal är 6 6 7 7 12 18
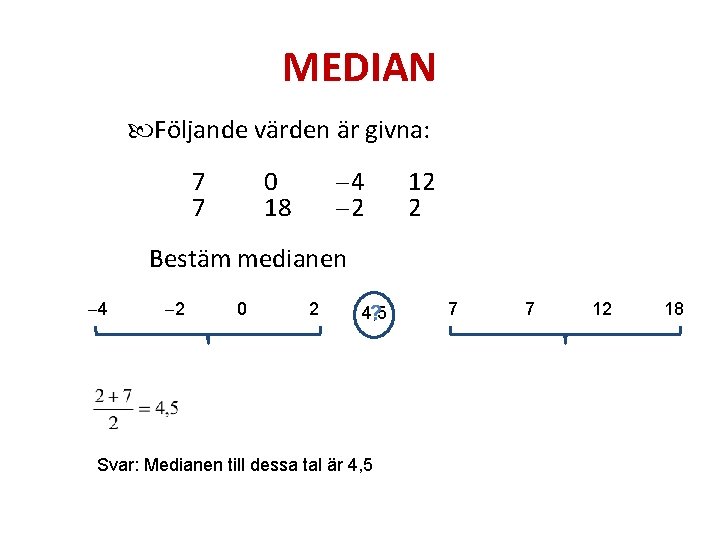
MEDIAN Följande värden är givna: 7 7 4 2 0 18 12 2 Bestäm medianen 4 2 0 2 4, 5 ? Svar: Medianen till dessa tal är 4, 5 7 7 12 18

Variationsbredd är: ”Det största värdet minus det minsta värdet. ” Exempel: Värden: 10, 12, 15, 17, 18, 20, 21, 23, 30 och 39. Variationsbredd: 39 – 10 = 29
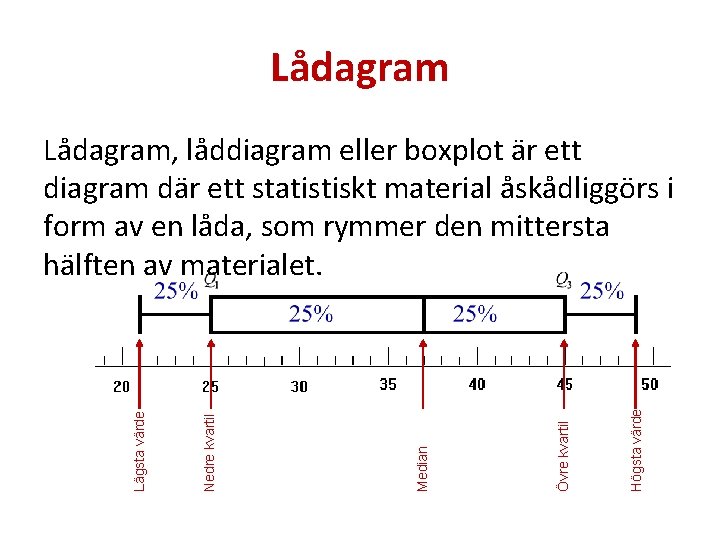
Lådagram Högsta värde Övre kvartil Median Nedre kvartil Lägsta värde Lådagram, låddiagram eller boxplot är ett diagram där ett statistiskt material åskådliggörs i form av en låda, som rymmer den mittersta hälften av materialet.

Lådagram – ett exempel Exempel på ett lådagram, som visar åldern på tolv personer som är 10, 12, 15, 17, 18, 20, 21, 23, 30 och 39 år gamla: Q 1 = 15, Q 2 = 19 (median) & Q 3 = 22
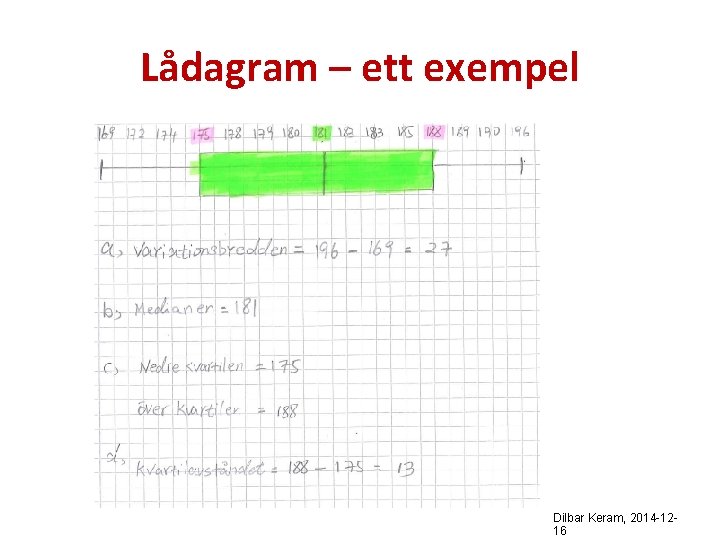
Lådagram – ett exempel Dilbar Keram, 2014 -1216

STANDARDAVVIKELSE Provresultat: 78 p, 68 p, 35 p, 80 p, 74 p & 21 p Medelvärde På (78+78+68+35+80+74+21)/7 = 62 räknaren: (16)² = 256 78 -62 = 16 (6)² = 36 68 -62 = 6 (-27)² = 729 35 -62 = -27 (18)² = 324 80 -62 = 18 (12)² = 144 74 -62 = 12 (-41)² = 1681 21 -62 = -41 256+36+729+324+144+1681 = 3426/(7 -1) = 571

STANDARDAVVIKELSE 1. 2. 3. 4. 5. 6. Beräkna medelvärdet Beräkna differensen mellan alla värden och medelvärdet Kvadrera alla svar i (2) Summera alla svar i (3) Dividera summan i (4) med 1 mindre än antalet värden Dra roten ur… Nu har du standardavvikelsen… Från formelbladet:

STANDARDAVVIKELSE 1. 2. 3. 4. 5. 6. Beräkna medelvärdet Beräkna differensen mellan alla värden och medelvärdet Kvadrera alla svar i (2) Summera alla svar i (3) Dividera summan i (4) med 1 mindre än antalet värden Dra roten ur… Nu har du standardavvikelsen… Vilken är standardavvikelsen till följande talmängd? 12, 19, 22, 17, 14, 23 & 20

STANDARDAVVIKELSE Provresultat: 78 p, 68 p, 35 p, 80 p, 74 p & 21 p I formelsamlingen ser standardavvikelsen ut så här
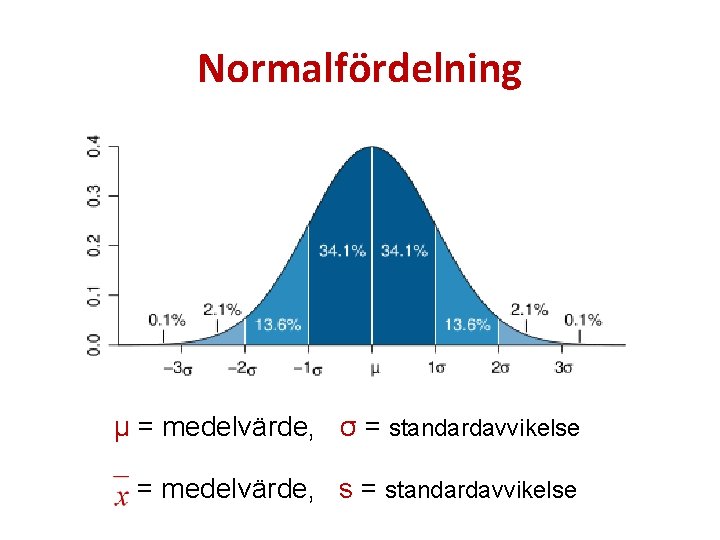
Normalfördelning μ = medelvärde, σ = standardavvikelse = medelvärde, s = standardavvikelse

MODELLERING – ETT EXEMPEL
MODELLERING – ETT EXEMPEL
- Slides: 102