Fast Multiscale Image Segmentation From Pixels to Semantics

Fast, Multiscale Image Segmentation: From Pixels to Semantics Ronen Basri The Weizmann Institute of Science Joint work with Achi Brandt, Meirav Galun, Eitan Sharon

Camouflage

Camouflage Malik et al. ’s “Normalized cuts”

Our Results

Segmentation by Weighted Aggregation A multiscale algorithm: • Optimizes a global measure • Returns a full hierarchy of segments • Linear complexity • Combines multiscale measurements: – Texture – Boundary integrity

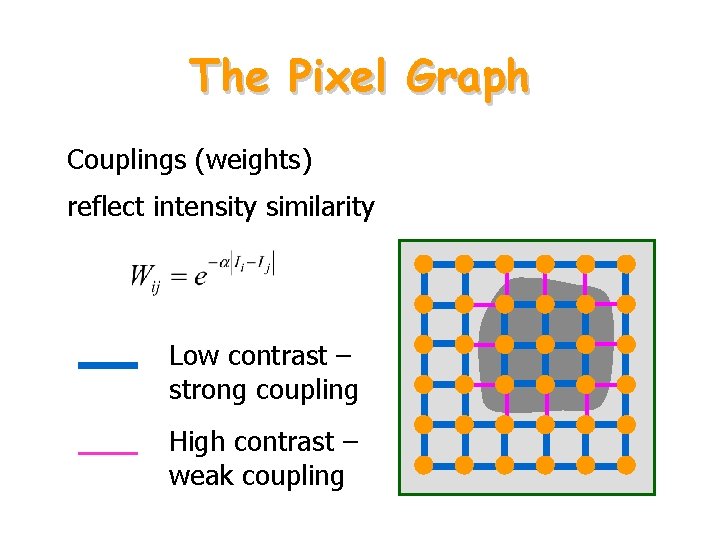
The Pixel Graph Couplings (weights) reflect intensity similarity Low contrast – strong coupling High contrast – weak coupling

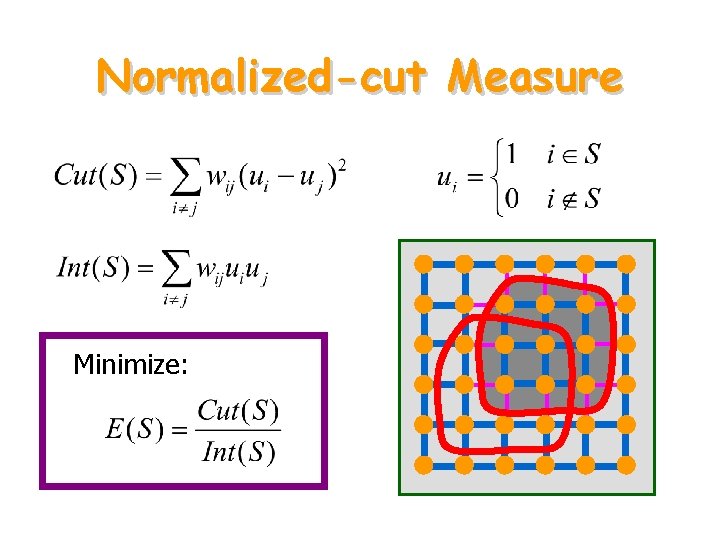
Normalized-cut Measure Minimize:

Saliency Measure Minimize:

Multiscale Computation of Ncuts • Our objective is to rapidly find the segments (0 -1 partitions) that optimize E. • For single-node cuts we simply evaluate E. • For multiple-node cuts we perform “soft contraction” using coarsening procedures from algebraic multigrid solvers of PDEs.

Coarsening the Graph • Suppose we can define a sparse mapping such that for all minimal states

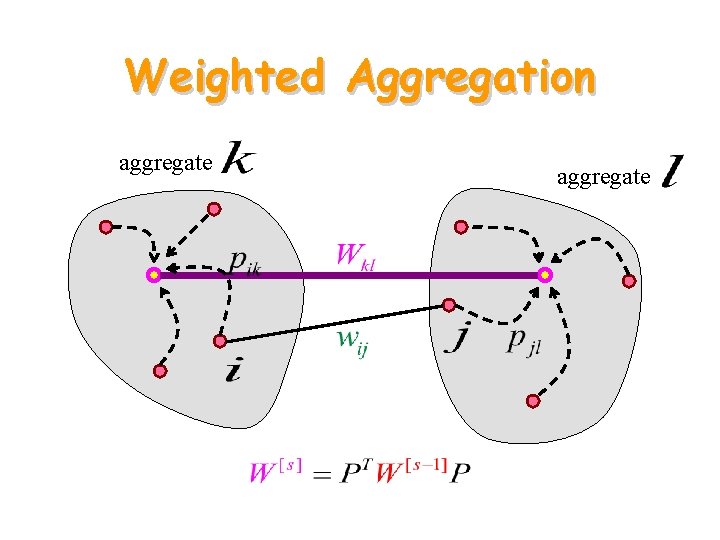
Coarse Energy • Then • PTWP, PTLP define a new (smaller) graph

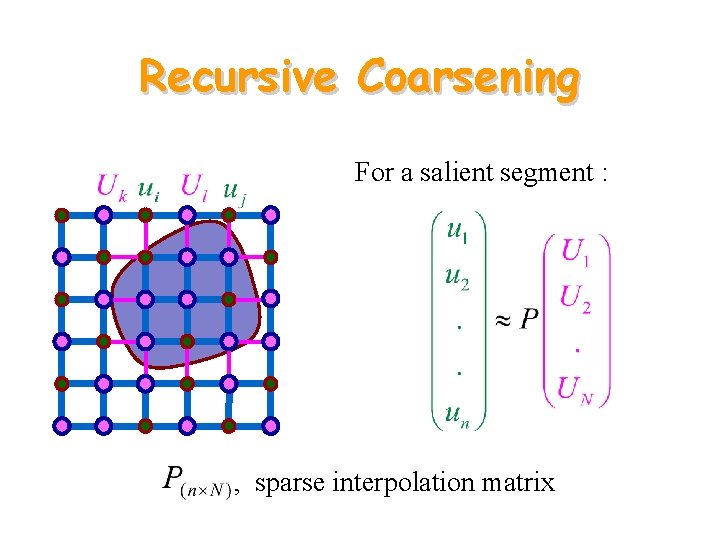
Recursive Coarsening

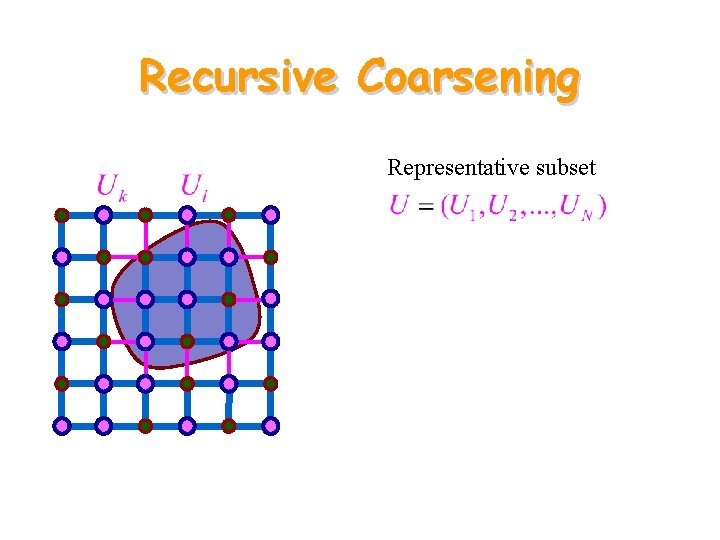
Recursive Coarsening Representative subset

Recursive Coarsening For a salient segment : , sparse interpolation matrix

Weighted Aggregation aggregate

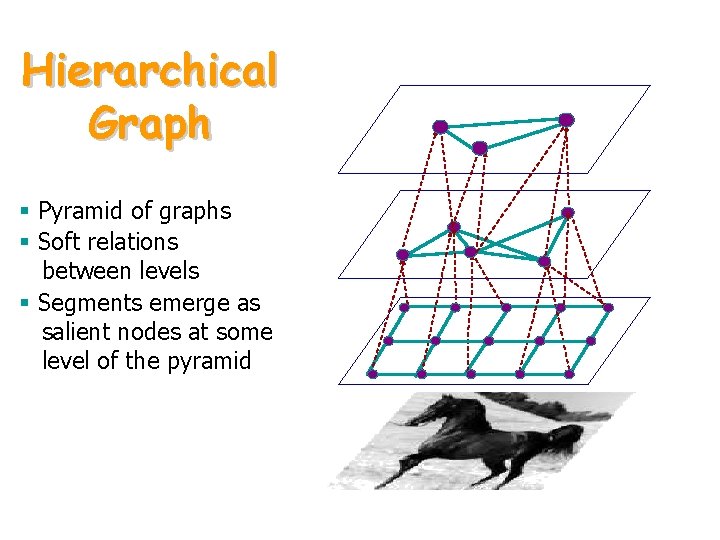
Hierarchical Graph § Pyramid of graphs § Soft relations between levels § Segments emerge as salient nodes at some level of the pyramid

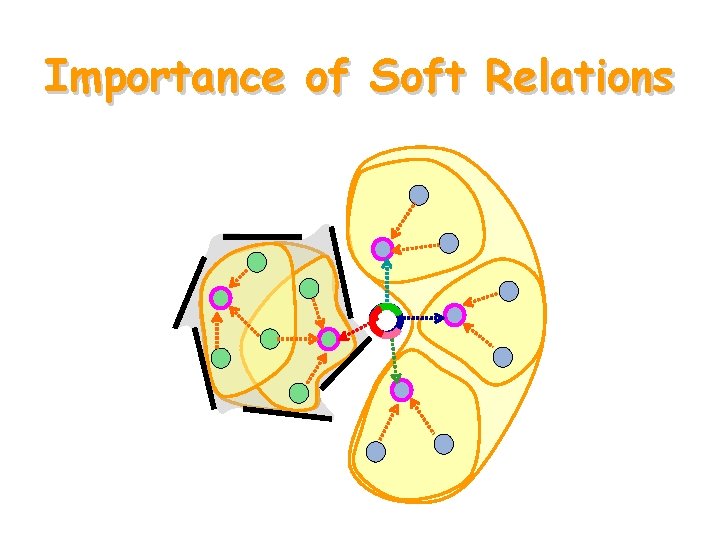
Importance of Soft Relations

Physical Motivation • Our algorithm is motivated by algebraic multigrid solutions to heat or electric networks • u - temperature/potential • a(x, y) – conductivity • At steady state largest temperature differences are along the cuts • AMG coarsening is independent of f

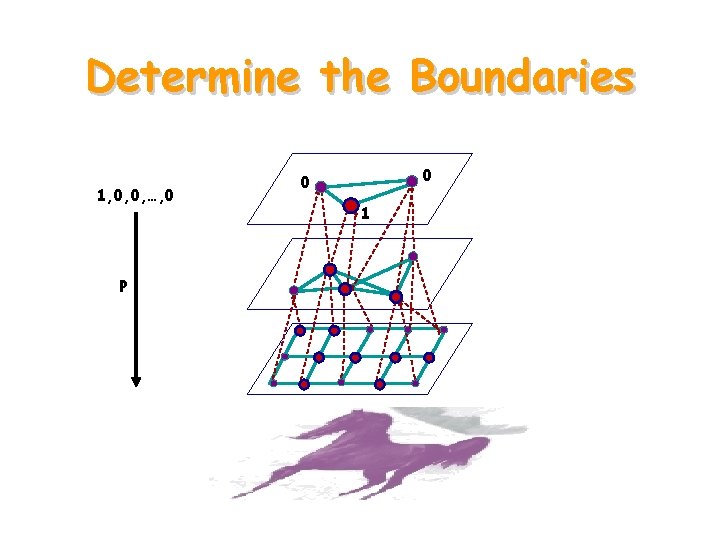
Determine the Boundaries 1, 0, 0, …, 0 P 0 0 1

Hierarchy in SWA

Texture Examples

Filters (From Malik and Perona) Oriented filters Centersurround

A Chicken and Egg Problem: Coarse measurements mix neighboring statistics Hey, I was here first Solution: Support of measurements is determined as the segmentation process proceeds

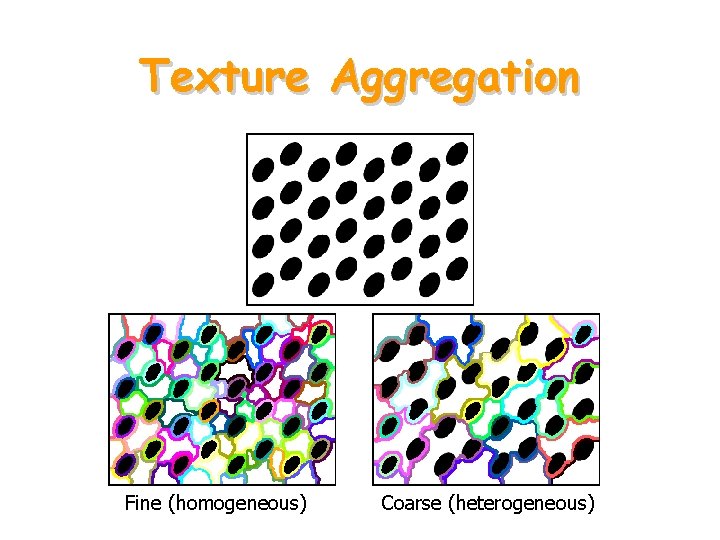
Texture Aggregation • Aggregates assumed to capture texture elements • Compare neighboring aggregates according to the following statistics: – Multiscale brightness measures – Multiscale shape measures – Filter responses • Use statistics to modify couplings

Recursive Computation of Measures • Given some measure of aggregates at a certain level (e. g. , orientation) • At every coarser level we take a weighted sum of this measure from previous level • The result can be used to compute the average, variance or histogram of the measure • Complexity is linear

Use Averages to Modify the Graph

Adaptive vs. Rigid Measurements Original Our algorithm - SWA Averaging Geometric

Adaptive vs. Rigid Measurements Original Our algorithm - SWA Interpolation Geometric

Adaptive vs. Rigid Measurements

Adaptive vs. Rigid Measurements

Adaptive vs. Rigid Measurements

Adaptive vs. Rigid Measurements

Adaptive vs. Rigid Measurements

Texture Aggregation Fine (homogeneous) Coarse (heterogeneous)

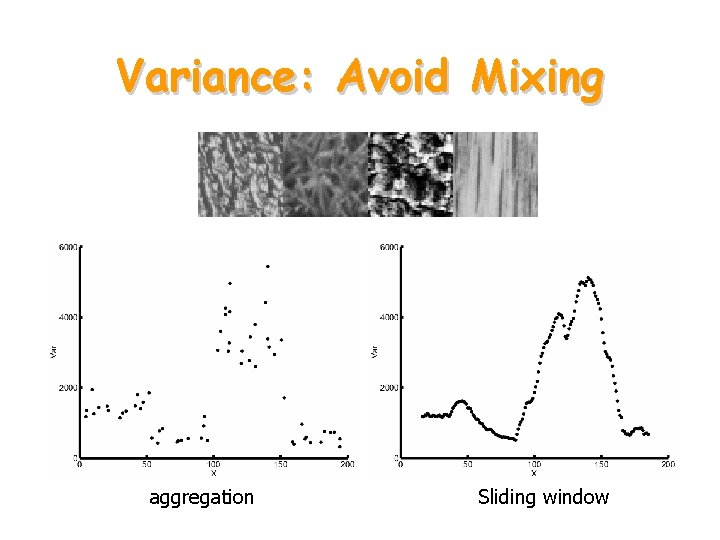
Multiscale Variance Vector

Multiscale Variance Vector

Variance: Avoid Mixing aggregation Sliding window

Leopard

More Leopards…

And More…

Birds

More Animals

Boat

Malik’s Ncuts

Key Differences • Optimize a global measure (like Malik’s Ncuts) • Hierarchy with soft relations (unlike agglomerative/graph contraction) • Combine texture measurements while avoiding the “chicken and egg problem”

Complexity • Every level contains about half the nodes of the previous level: Total #nodes 2 X #pixels • All connections are local, cleaning small weights • Top-down sharpening: constant number of levels • Linear complexity • Implementation: 5 seconds for 400 x 400

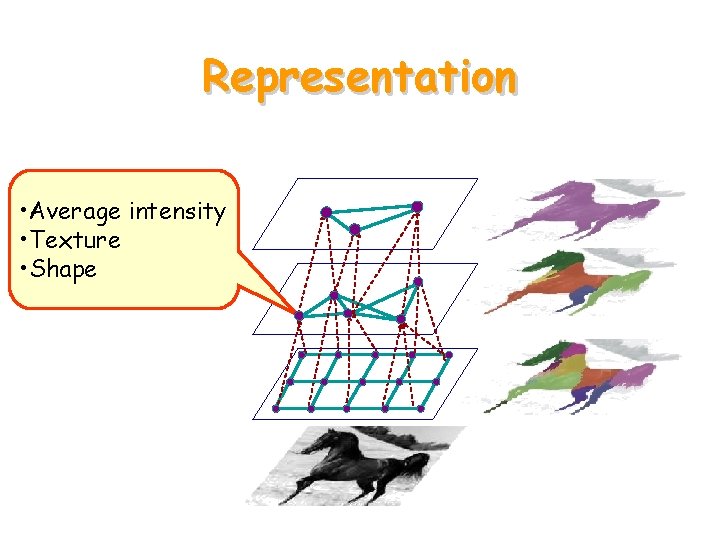
Representation • Average intensity • Texture • Shape

Matching (with Chen Brestel)

More…

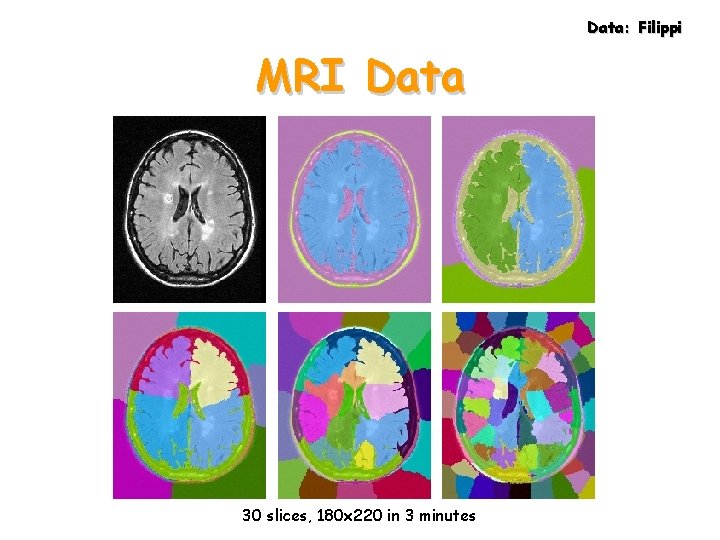
Data: Filippi MRI Data 30 slices, 180 x 220 in 3 minutes

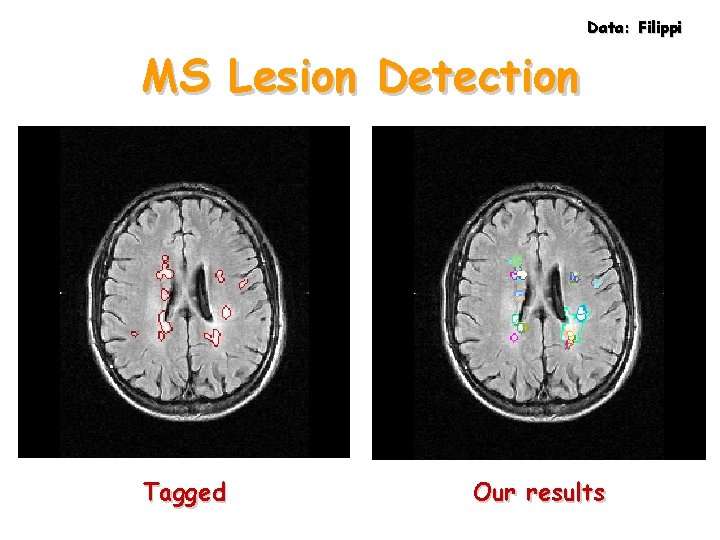
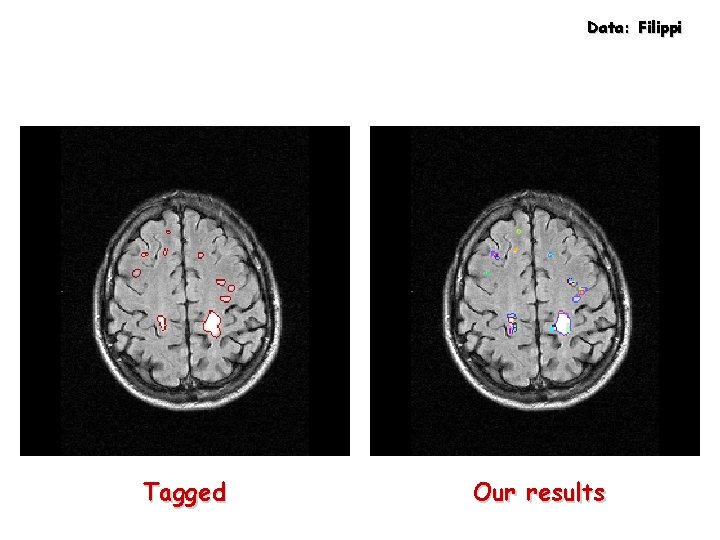
Data: Filippi MS Lesion Detection Tagged Our results

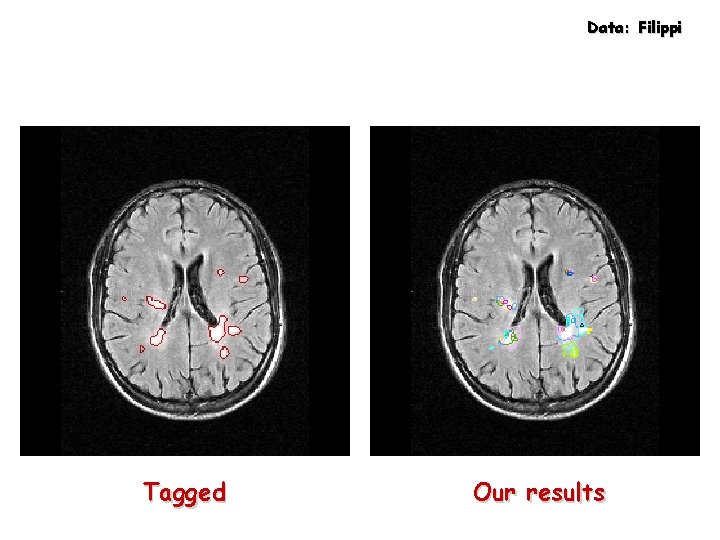
Data: Filippi Tagged Our results

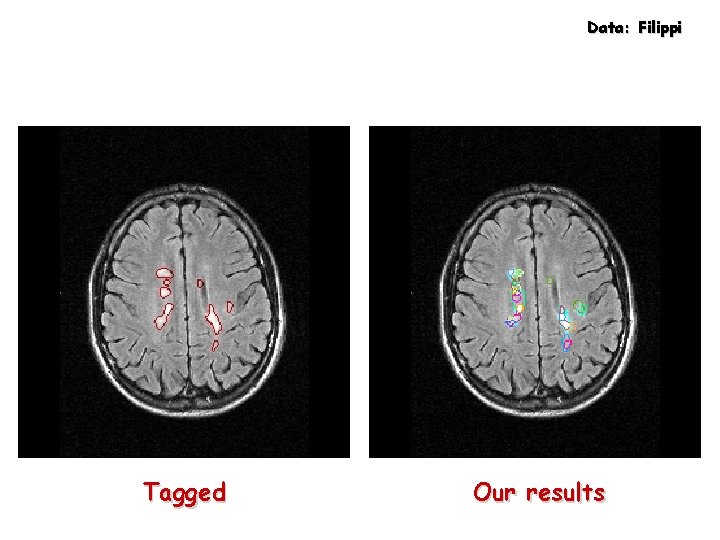
Data: Filippi Tagged Our results

Data: Filippi Tagged Our results

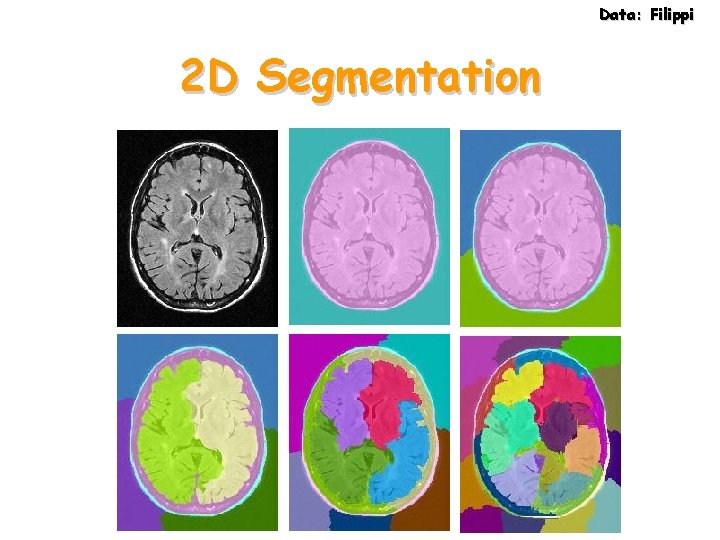
Data: Filippi 2 D Segmentation

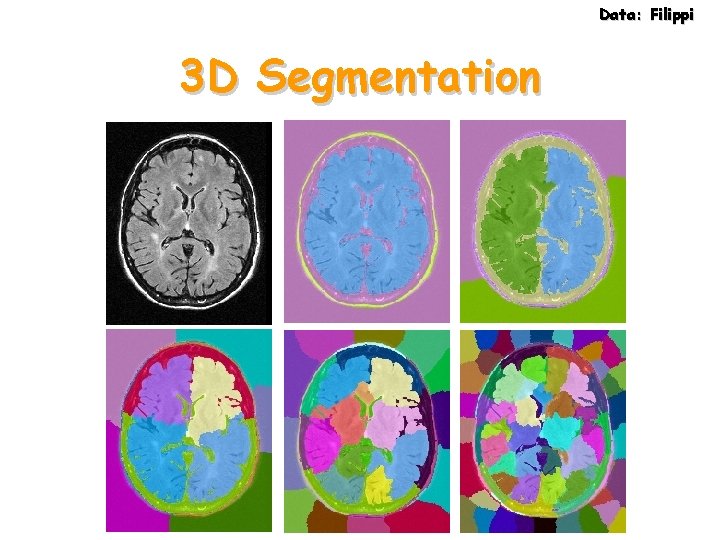
Data: Filippi 3 D Segmentation

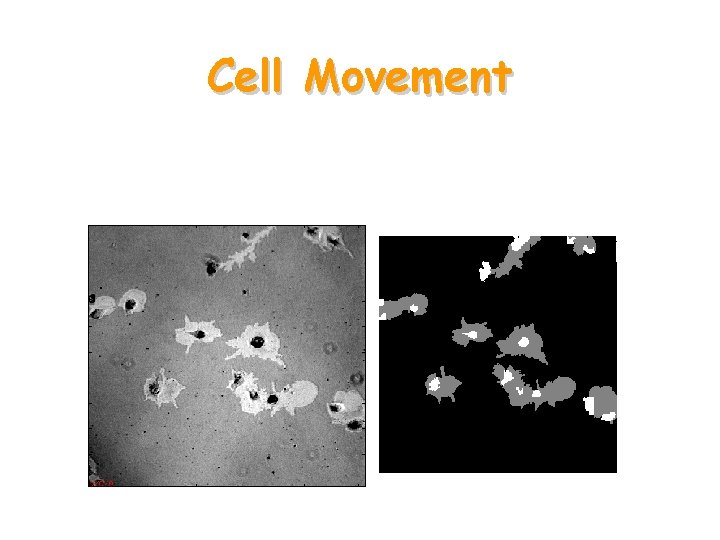
Cell Movement

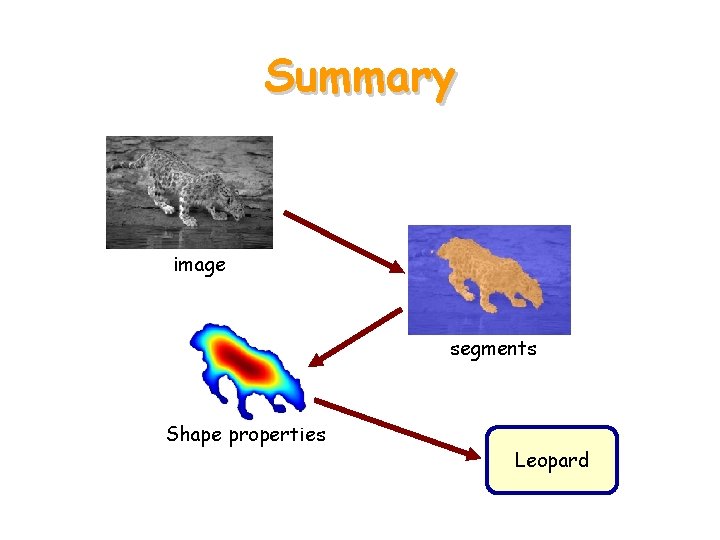
Summary image segments Shape properties Leopard