Elementos del movimiento Unidad 11 2 Contenidos 1

Elementos del movimiento Unidad 11

2 Contenidos (1) 1. - Introducción. 2. - Magnitudes escalares y vectoriales. 3. - Sistemas de referencia. Concepto de movimiento. 4. - Operaciones con vectores. 5. - Trayectoria, posición y desplazamiento. 6. - Velocidad media e instantánea (introducción al concepto de derivada).

3 Contenidos (2) 7. - Aceleración media e instantánea. 8. - Componentes intrínsecas de la aceleración: tangencial y normal. .

Magnitudes escalares y vectoriales 4 RE PA SO • Escalares: quedan perfectamente definidas con una cantidad (número) y una unidad – Ejemplo: el tiempo 3 s; la masa 8 kg. • Vectoriales (vectores): Se caracterizan por: – Módulo: (cantidad y unidad). Se representa por la longitud del vector. Es la parte escalar. – Dirección: es la recta que contiene el vector. – Sentido: indicado por la punta de la flecha. – Punto de aplicación: origen de la flecha. – Ejemplo: la posición, velocidad, fuerza. . .

5 Sistema de referencia y movimiento • Es un punto del espacio respecto al cual describimos el movimiento. • Un objeto se encuentra en movimiento si cambia su posición respecto al sistema de referencia. • Los sistemas de referencia cuentan a su vez con uno (x), dos (x, y) o tres ejes (x, y, z), perpendiculares entre sí, según trabajemos en una recta, en un plano, o en el espacio.

6 Representación de un sistema de referencia tridimensional. • Sobre cada eje se toma como unidad de medida los vectores unitarios (módulo igual a 1): – i sobre el eje x – j sobre el eje y – k sobre el eje z y k z j i x

Vectores • Se representan con una flecha encima de la letra que utilizada para dicha magnitud. • Se suelen expresar en forma cartesiana en donde ax, ay y az son sus componentes cartesianas: • a = ax · i + a y · j + az · k • A partir de ahora, los vectores los escribiremos en negrita y diferente color para mayor comodidad: • a = ax · i + ay · j + az · k • en donde i, j y k representan los vectores unitarios sobre los ejes x, y, z. 7

Suma de vectores • Sean dos vectores: a = ax · i + ay · j + az · k y b = bx · i + by · j + bz · k • El vector suma vendrá dado por: a + b = (ax + bx) · i + (ay + by) · j + (az + bz) · k • Ejemplo: Sean y a = 3 i + 2 j a 5 y b = 2 i – 3 j x a + b = (3+2) i + (2 – 3) j b = 5 i – j 8

Cálculo del módulo de un vector. • Sean un vector: a = ax · i + ay · j + az · k • El módulo de a, que se representa como |a| se calcula aplicando el teorema de Pitágoras: • ______ |a| = ax 2 + ay 2 + az 2 • Ejemplo: En el vector anterior c = a + b= 5 i – j • ____________ ___ |a| = ax 2 + ay 2 + az 2 = 52 + (– 1)2 + 02 = 26 9

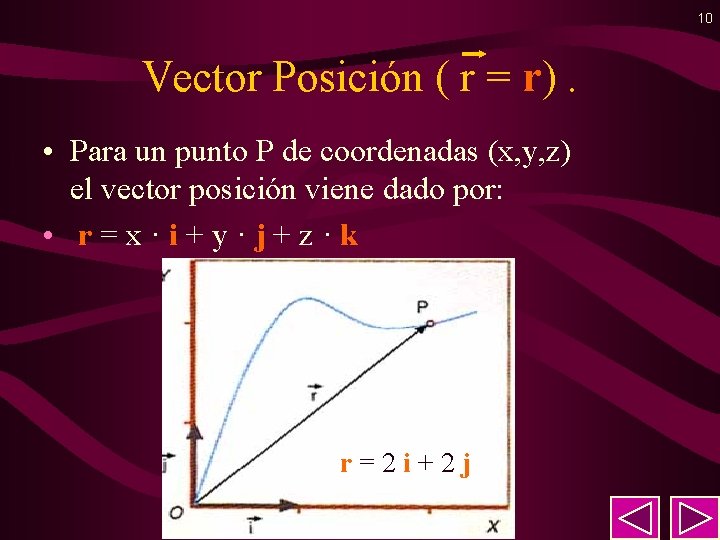
10 Vector Posición ( r = r). • Para un punto P de coordenadas (x, y, z) el vector posición viene dado por: • r = x · i + y · j + z · k r = 2 i + 2 j

Representación de vectores posición v = x · i + y · j • En dos dimensiones v = x · i + y · j + z · k • En tres dimensiones 11

12 Ecuación del movimiento • La ecuación que proporciona la posición de un objeto con respecto al tiempo se llama “ecuación del movimiento”: ecuación del movimiento • r(t) = x(t) · i + y(t) · j +z(t) · k • Ejemplo: r(t) = [2 t · i + (1–t) · j + (3 t 2+4) · k] m • En el S. I. la unidad será el m.

Ejercicio: Sea el movimiento definido por la si- 13 guiente ecuación r = 2 t i + 8 j en unidades del S. I. Dibujar los vectores posición en los instantes 0, 2, 4 y 6 segundos. • • • t (s) r (m) 0 8 j (0, 8) 2 4 i + 8 j (4, 8) 4 8 i + 8 j (8, 8) 6 12 i + 8 j (12, 8) y 10 5 5 10 x

14 Ecuaciones paramétricas. • Son las ecuaciones que relacionan cada componente cartesiana con el tiempo. • x = f(t); y = g(t); z = h(t) • Son ecuaciones escalares (no vectores). • Ejemplo: En el vector: Ejemplo: r(t) = [2 t·i + (1–t) ·j + (3 t 2+4)·k] m • las ecuaciones paramétricas serían: • x = 2 t ; y = 1 – t ; z = 3 t 2 + 4

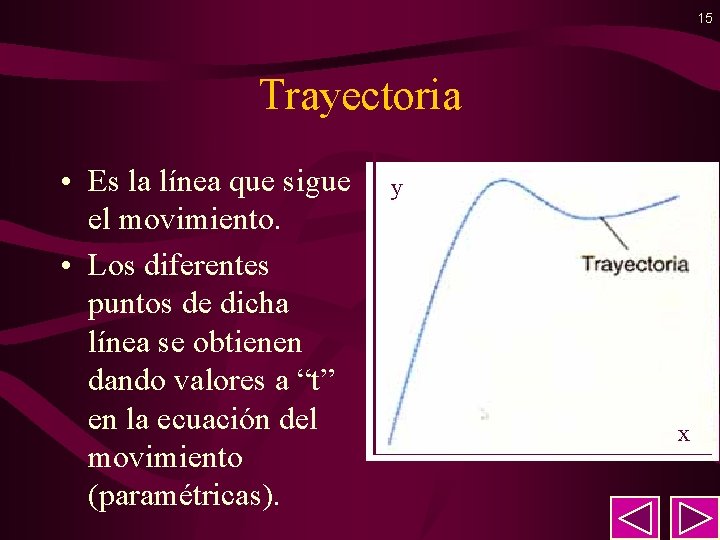
15 Trayectoria • Es la línea que sigue el movimiento. • Los diferentes puntos de dicha línea se obtienen dando valores a “t” en la ecuación del movimiento (paramétricas). y x

16 Ecuaciones de la trayectoria. • Se obtienen despejando el parámetro (tiempo) en una ecuación y sustituyendo el valor en la otra. • Son ecuaciones escalares (no vectores). • Ejemplo: r(t) = [2 t·i + (1–t) ·j + (3 t 2+4)·k] m • x = 2 t ; y = 1 – t ; z = 3 t 2 + 4 • t = x/2 y = 1 – x/2 ; z = 3 x 2/4 + 4 • En el caso del espacio bidimensional, únicamente existe una ecuación de la trayectoria: y = f(x).

17 Ejercicio: Determinar las ecuaciones paramétricas y de la trayectoria del siguiente movimiento expresado por la ecuación: r(t) = [(t – 2)·i + (2 t 2 + 4 t – 3 )·j] m • • Ecuaciones paramétricas: x = t – 2 ; y = 2 t 2 + 4 t – 3 Despejando “t”de la 1ª ecuación: t = x + 2 Y sustituyendo en la segunda: y = 2 (x + 2)2 + 4·(x + 2) – 3 y = 2 (x 2 + 4 x + 4) + 4·(x + 2) – 3 y = 2 x 2 + 8 x + 8 + 4 x + 8 – 3 Ecuación de la trayectoria: y = 2 x 2 + 12 x + 13

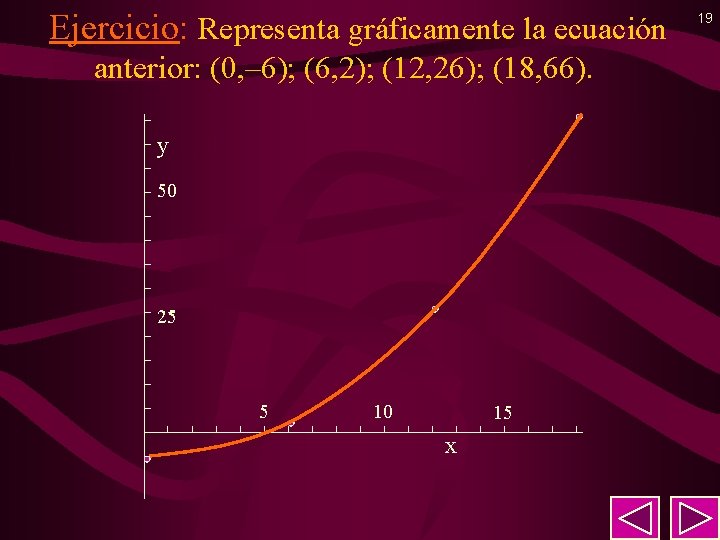
Ejercicio: Determina el valor del vector posición del vector : r(t) = [3 t · i + (2 t 2 – 6) · j] m en los instantes de tiempo t = 0, 2, 4, 6 s y calcula el módulo de dichos vectores y la ecuación de la trayectoria. t (s) 0 2 r(t) (m) – 6 j r(t) (m) ——— (– 6)2 ———— 6 i + 2 j 62 + 22 —————— = 6, 00 = 6, 32 4 12 i + 26 j 122 + 262 = 28, 64 —————— 6 18 i + 66 j 182 + 662 = 68, 41 • Despejando “t” de x = 3 t t = x/3, y sustituyendo en y = 2 t 2 – 6 queda: y = 2(x/3)2 – 6; y = 2 x 2/9 – 6 18

Ejercicio: Representa gráficamente la ecuación anterior: (0, – 6); (6, 2); (12, 26); (18, 66). y 50 25 5 10 15 x 19

20 Vector desplazamiento ( r = r) • Es el vector diferencia de dos vectores de posición en dos momentos distintos. • Sean r 0 = x 0 i + y 0 j + z 0 k y r 1 = x 1 i + y 1 j + z 1 k dos vectores posición. • r = r 1 – r 0 = = (x 1–x 0) i + (y 1–y 0) j + (z 1–z 0) k = = x i + y j + z k • En el S. I. la unidad será el m.

Ejercicio: Cuál será el vector desplazamiento y 21 cuánto valdrá su módulo en la ecuación anterior: r(t) = 3 t · i + (2 t 2 – 6) · j en unidades del S. I entre los instantes t = 2 s y t = 4 s. • r 1 (t =2 s) = (6 i + 2 j) m r 2 (t= 4 s) = (12 i + 26 j) m • r = r 2 – r 1 = x i + y j + z k = • [(12 – 6) i + (26 – 2) j] m • • r = (6 i + 24 j) m ———– 2 2 r = 6 + 24 m = 36 + 576 m = 24, 74 m

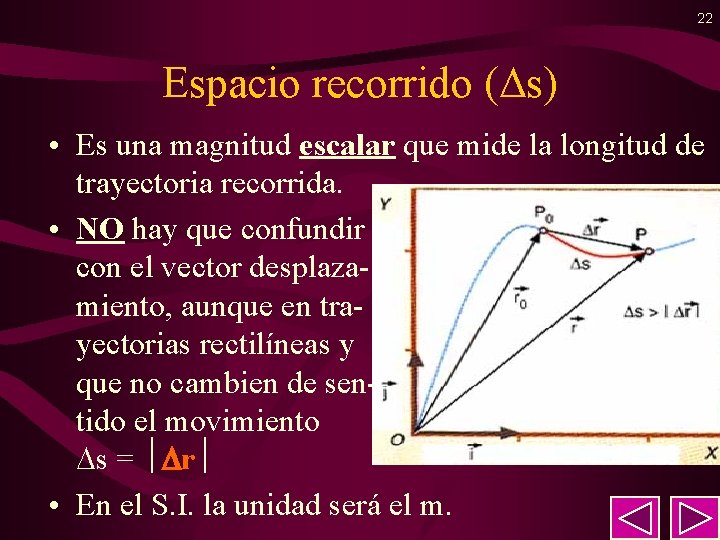
22 Espacio recorrido ( s) • Es una magnitud escalar que mide la longitud de trayectoria recorrida. • NO hay que confundir con el vector desplazamiento, aunque en trayectorias rectilíneas y que no cambien de sentido el movimiento s = r • En el S. I. la unidad será el m.

23 Velocidad media (vm = vm) • r x i + y j + z k vm = ———————— t t • x y z vm = —— i + —— j + —— k t t t vm = vmx i + vmy j + vmz k • El módulo del vector vm toma el valor: ——————— vm = vmx 2 + vmy 2 + vmz 2

24 Velocidad media (continuación) • La dirección y el sentido son los mismos que los del vector desplazamiento r ya que t es un escalar. • NO hay que confundir vm con el escalar s/ t que, en Física, llamaremos rapidez o celeridad media. • Ni siquiera vm tiene porqué coincidir con la rapidez o celeridad media. – Ejemplo: un corredor que da una vuelta completa a un circuito tendrá vm = 0 ya que r = 0. Sin embargo tiene una rapidez que viene determinada por la longitud de la pista ( s) dividido por el tiempo empleado en cubrir la vuelta ( t). • En el S. I. la unidad será el m/s.

Ejercicio: Calcular la velocidad media entre los instantes t = 2 s y t = 5, así como su módulo en el movimiento: r(t) = [(2 t 2 – 4) · i + (1 – 4 t) · j] m r 1 (t =2 s) = (4 i – 7 j) m r 2 (t =5 s) = (46 i – 19 j) m r (2 s 5 s) = r 2 – r 1 = (42 i – 12 j) m r (42 i – 12 j) m vm (2 s 5 s) = —————— = (14 i – 4 j) m/s t 5 s– 2 s ————— vm (2 s 5 s) = (14 m/s)2 + (– 4 m/s)2 = 14, 56 m/s 25

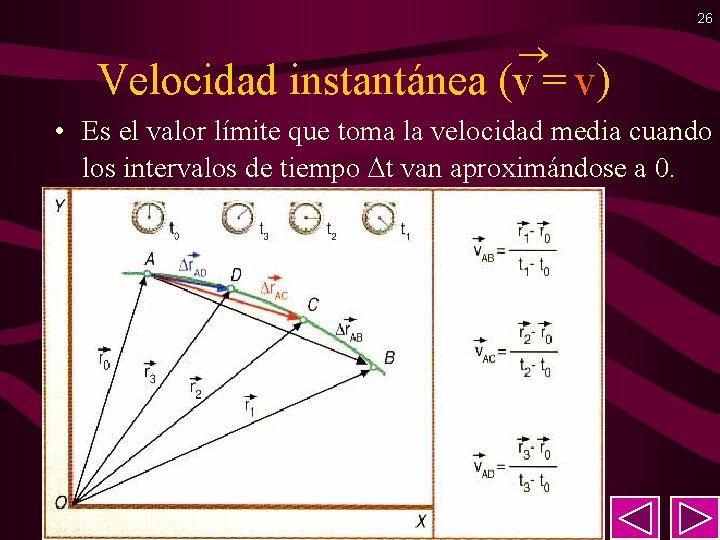
26 Velocidad instantánea (v = v) • Es el valor límite que toma la velocidad media cuando los intervalos de tiempo t van aproximándose a 0.

27 Ejemplo: Calcular la velocidad instantánea aproximada ( t = 0, 1 s) en el instante t = 2 s, así como su módulo en el movimiento: r(t) = [3 t i + (2 t 2– 6) j] m • Sea t = 0, 1 s, suficientemente pequeño: deberemos conocer la posición en r 1 (t =2 s) y en r 2 (t =2, 1 s) • r 1 (t =2 s) = (6 i + 2 j) m • r 2 (t =2, 1 s) = (6, 3 i + 2, 82 j) m • r = r 2 – r 1 = (0, 3 i + 0, 82 j) m • r (0, 3 i + 0, 82 j) m vaprox (t=2 s) = ——————— = (3 i + 8, 2 j) m/s t 0, 1 s • ———— vaprox (t=2 s) = 32 + 8, 22 m/s = 8, 73 m/s

Ejercicio: Calcular la velocidad instantánea más 28 aproximada en el instante t = 2 s, así como su módulo en el movimiento: r(t) = [3 t · i + (2 t 2 – 6) · j] m • Si queremos calcular v (t=2 s) de forma más aproximada deberemos tomar un t aún menor, por ejemplo 0, 01 s, y conocer la posición en r 1 (t =2 s) y en r 3 (t =2, 01 s). • r 1 (t =2 s) = (6 i + 2 j) m • r 3 (t =2, 01 s) = (6, 03 i + 2, 0802 j) m • r = r 3 – r 1 = (0, 03 i + 0, 0802 j) m • • r (0, 03 i + 0, 0802 j) m vaprox (t=2 s) = ———————— = (3 i + 8, 02 j) m/s t 0, 01 s ————— 2 2 vaprox (t=2 s) = 3 + 8, 02 m/s = 8, 56 m/s

29 Componentes cartesianas de la velocidad instantánea v • r x i + y j + z k v = lim ———————— t 0 t • dr dx dy dz v = —— i + —— j + —— k dt dt • v = vx i + vy j + vz k

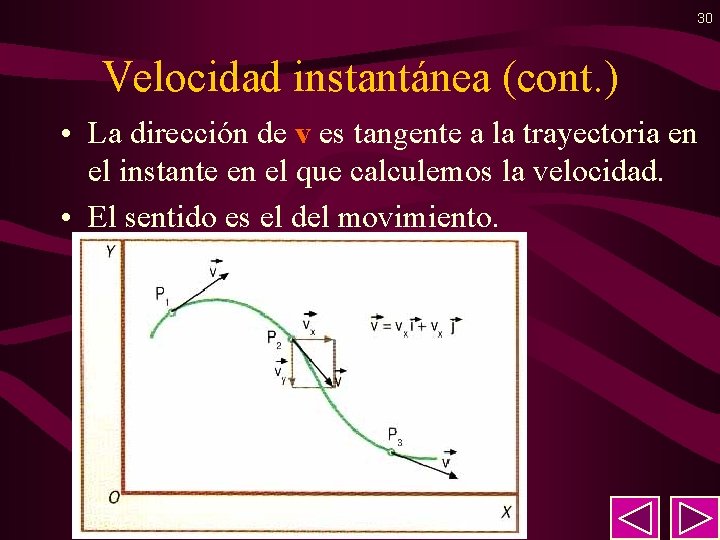
30 Velocidad instantánea (cont. ) • La dirección de v es tangente a la trayectoria en el instante en el que calculemos la velocidad. • El sentido es el del movimiento.

Ejemplo: Calcular la expresión del vector 31 velocidad del movimiento anterior: r(t) = [3 t · i + (2 t 2 – 6) · j] m y la velocidad en los instantes 0, 2, 4 y 6 s así como su módulo. • r x i + y j + z k v = lim ———————— t 0 t • 3(t+ t) – 3 t [2(t+ t)2– 6 – [2 t 2– 6] v = ————— i + ————— j = t t • 3 t + 3 t – 3 t [2 t 2 + 4 t t + 2( t)2– 6]–[2 t 2– 6] = —————— i + ——————— j = t t • v = dr/dt = 3 i + 4 t j ya que t 0 Ecuación de la velocidad

Ejemplo (continuación): Calcular la expresión del vector velocidad del movimiento anterior r(t) = [3 t · i + (2 t 2 – 6) · j] m y la velocidad en los instantes 0, 2, 4 y 6 s así como su módulo. • Ecuación de la velocidad: v = 3 i + 4 t j t (s) 0 2 4 6 v(t) (m/s) — 2 3 i 3 ——— 3 i + 8 j 32 + 82 ———– 3 i + 16 j 32 + 162 ———– 3 i + 24 j 32 + 242 =3 = 8’ 54 = 16’ 28 = 24’ 19 32

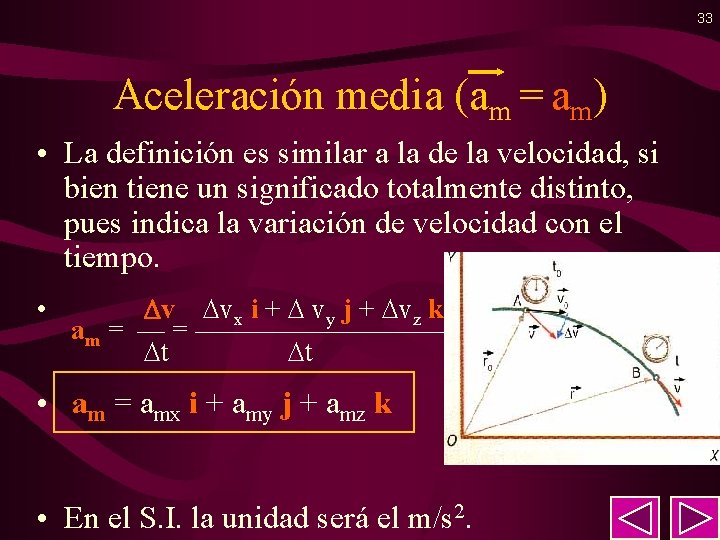
33 Aceleración media (am = am) • La definición es similar a la de la velocidad, si bien tiene un significado totalmente distinto, pues indica la variación de velocidad con el tiempo. • v vx i + vy j + vz k am = ————— t t • am = amx i + amy j + amz k • En el S. I. la unidad será el m/s 2.

34 Aceleración instantánea (a = a). • v vx i + vy j + vz k a = lim ————— t 0 t • dvx dvy dvz a = —— i + —— j + —— k dt dt • a = ax i + a y j + az k • La dirección y el sentido de a son los mismos que los del vector incremento de velocidad v ya que t es un escalar.

Ejemplo: Calcular la expresión del vector acelera- 35 ción del movimiento anterior r(t) = 3 t·i + (2 t 2– 6)·j, cuyo vector velocidad era v = 3 i + 4 t j en los instantes 0, 2, 4 y 6 s así como su módulo. • Ecuación del movimiento (de la posición): r(t) = 3 t·i + (2 t 2– 6)·j • Ecuación de la velocidad: v = 3 i + 4 t j • Ecuac. de la aceleración: a = dv/dt = 4 j • Para todos los valores de tiempo a = 4 j m/s 2, ya que se observa que a no depende de “t”. • — a (m/s 2) = 42 m/s 2 = 4 m/s 2

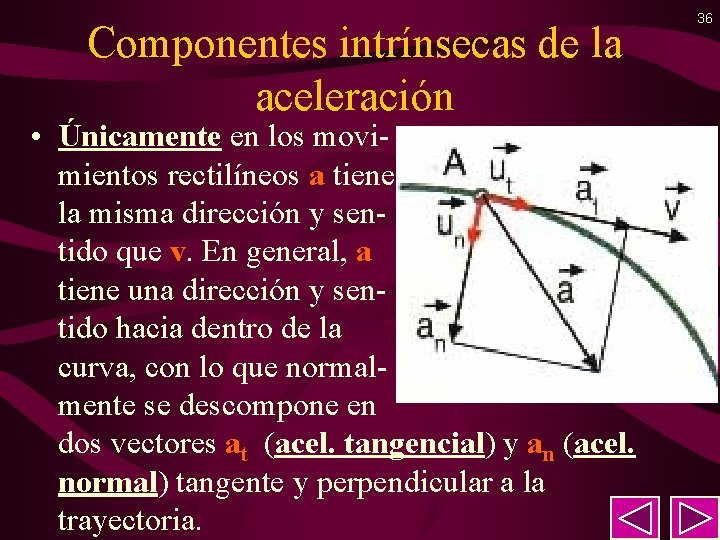
Componentes intrínsecas de la aceleración • Únicamente en los movimientos rectilíneos a tiene la misma dirección y sentido que v. En general, a tiene una dirección y sentido hacia dentro de la curva, con lo que normalmente se descompone en dos vectores at (acel. tangencial) y an (acel. normal) tangente y perpendicular a la trayectoria. 36

Componentes intrínsecas de la aceleración (at y an) • a = at + an = at ·ut + an·un siendo ut y un los vectores unitarios tangente y perpendicular a la trayectoria en el punto en el que calculamos la aceleración. • v d v v 2 at= at = lim —— = —— ; an= an = —— t 0 t dt R • siendo R el radio de curvatura de la trayectoria. • Suele llamarse v = v at= dv/dt ; an= v 2/R • ——— Igualmente llamamos a = at 2 + an 2 37

Ejemplo: Un coche de carreras toma la salida en una pista circular de 1 km de radio. El módulo de la velocidad aumenta según la ecuación: v(t) = 7 t, en unidades del SI. Calcula: a) la aceleración tangencial; b) la aceleración normal y el módulo del vector a a los 6 s. a) dv 7(t+ t) – 7 t 7 t + 7 t – 7 t 7 t at = —————— = 7 m/s 2 dt t at = 7 ut m/s 2 b) v 2 49 t 2 m 2·s-2 an = ————— = 0, 049 t 2 m/s 2 R 1000 m an (t= 6 s) = 0, 049 · 62 m/s 2 = 1, 76 m/s 2 ; an = 1, 76 un m/s 2 ————— 2 2 a (t= 6) = at + an = 72 + 1, 7642 m/s 2 = 7, 2 m/s 2 38