Movimiento rectilneo uniforme M R U Objetivos Identificar

Movimiento rectilíneo uniforme. (M. R. U. ) Objetivos: Identificar características de la Cinemática del Movimiento rectilíneo, en fenómenos naturales y situaciones cotidianas. Analizar conceptos de Cinemática mediante herramientas gráficas y analíticas los movimientos rectilíneos de un objeto en situaciones cotidianas.

REPASO………

Características de M. R. U. Si una partícula se mueve en la dirección del eje X con velocidad constante posee un Movimiento Rectilíneo Uniforme: constante: no cambia en el tiempo.

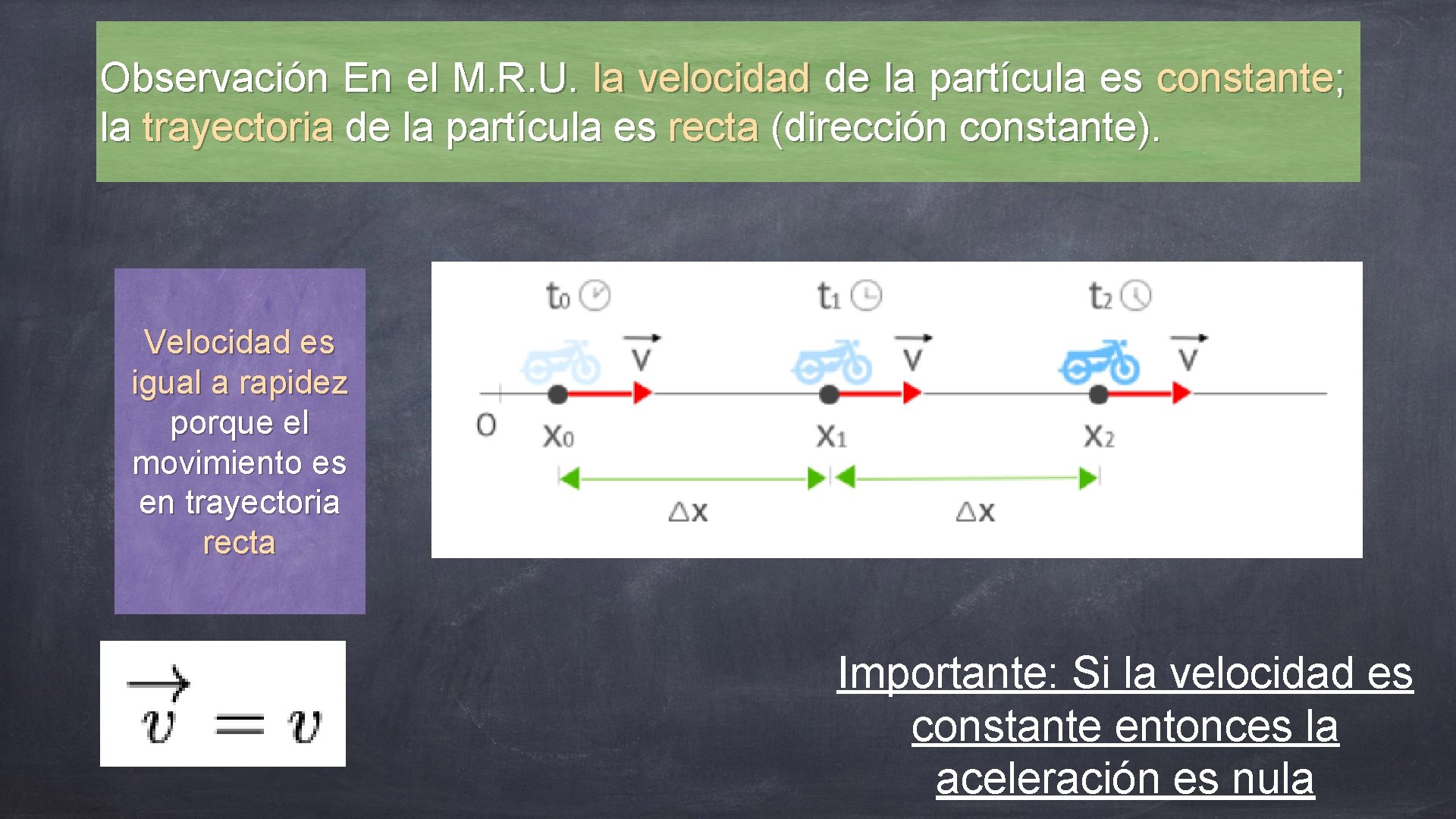
Observación En el M. R. U. la velocidad de la partícula es constante; la trayectoria de la partícula es recta (dirección constante). Velocidad es igual a rapidez porque el movimiento es en trayectoria recta Importante: Si la velocidad es constante entonces la aceleración es nula

ECUACIÓN ITINERARIO DEL M. R. U. Una partícula se mueve en la dirección del eje X. En el instante inicial (ti) se encuentra en la posición inicial (xi) y en un instante posterior (tf) en la posición final (xf), entonces la rapidez (v) de la partícula está dada por la ecuación: En particular si ti = 0, entonces se obtiene: Despejando posición final xf , se obtiene la ecuación itinerario:

¿Qué significa ECUACIÓN ITINERARIO DEL M. R. U. ? Posición de la partícula La posición de la partícula es una función del tiempo, es decir, la posición está dada por la coordenada x para un valor de t. Esta función se escribe así: x = f(t), y se representa por la ecuación itinerario.

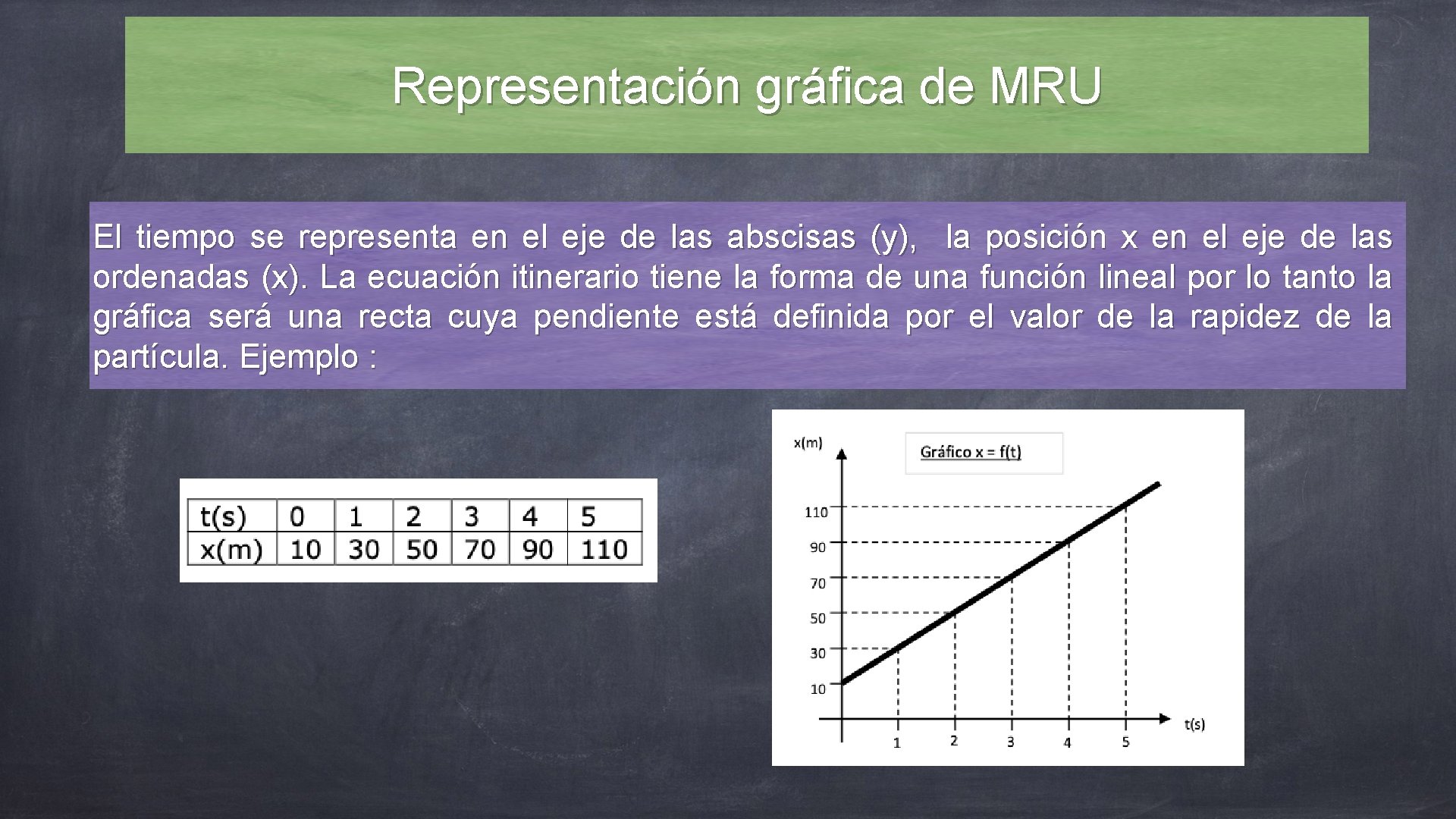
Representación gráfica de MRU El tiempo se representa en el eje de las abscisas (y), la posición x en el eje de las ordenadas (x). La ecuación itinerario tiene la forma de una función lineal por lo tanto la gráfica será una recta cuya pendiente está definida por el valor de la rapidez de la partícula. Ejemplo :

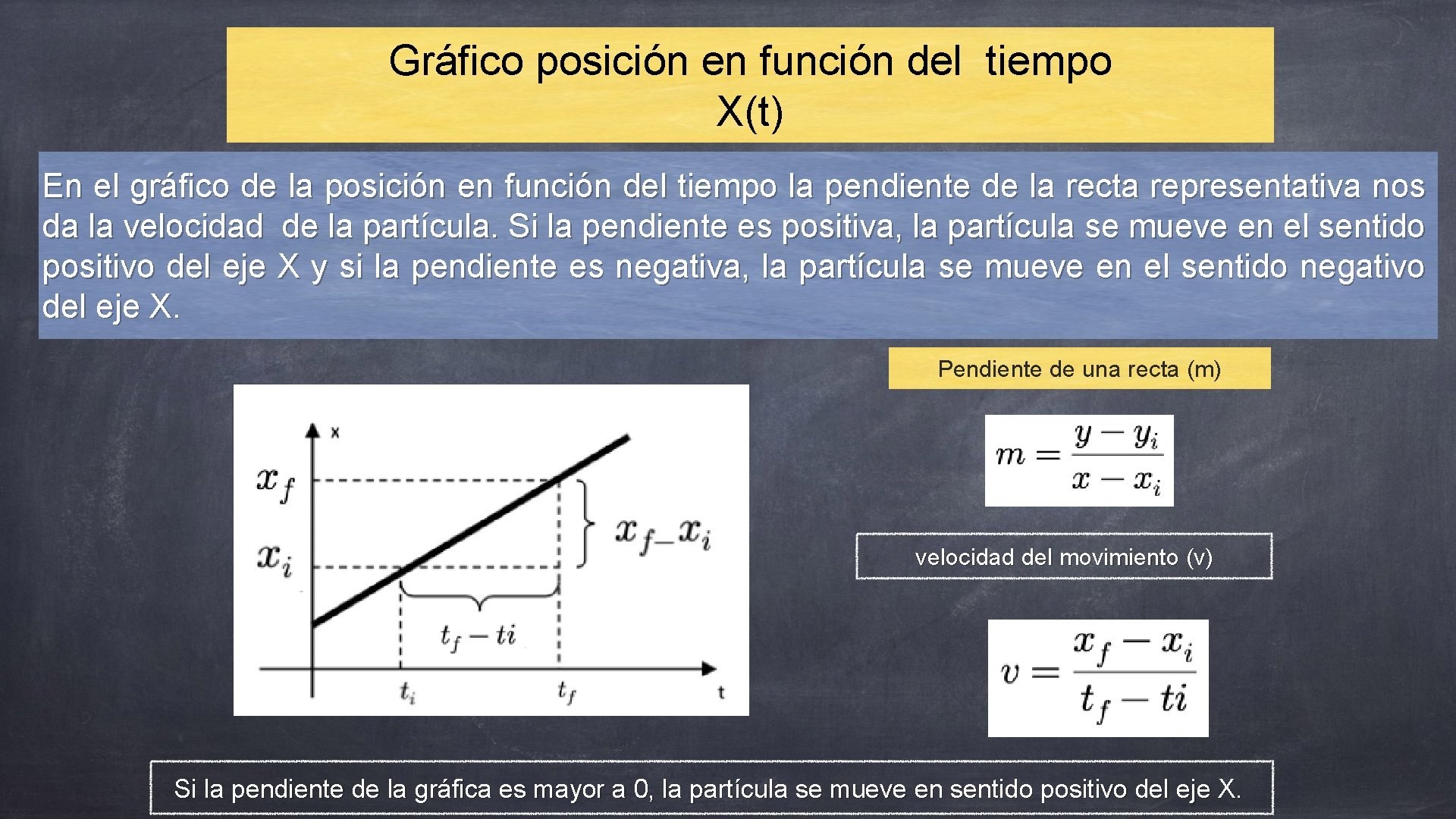
Gráfico posición en función del tiempo X(t) En el gráfico de la posición en función del tiempo la pendiente de la recta representativa nos da la velocidad de la partícula. Si la pendiente es positiva, la partícula se mueve en el sentido positivo del eje X y si la pendiente es negativa, la partícula se mueve en el sentido negativo del eje X. Pendiente de una recta (m) velocidad del movimiento (v) Si la pendiente de la gráfica es mayor a 0, la partícula se mueve en sentido positivo del eje X.

Ejemplo 1: Mediante la ecuación itinerario de una partícula que es: x = 4 + 5 · t. Realiza una tabla de datos donde t este expresado en horas, y x, en kilómetros. Completamos una tabla x-t y hacemos su representación gráfica. Posición (km) 4 9 14 24 34 Tiempo (h) 0 1 2 4 6 Estudiando la gráfica deducimos que se trata de un movimiento rectilíneo uniforme. Los parámetros de la ecuación son: Comprobemos las posiciones del móvil para graficar.

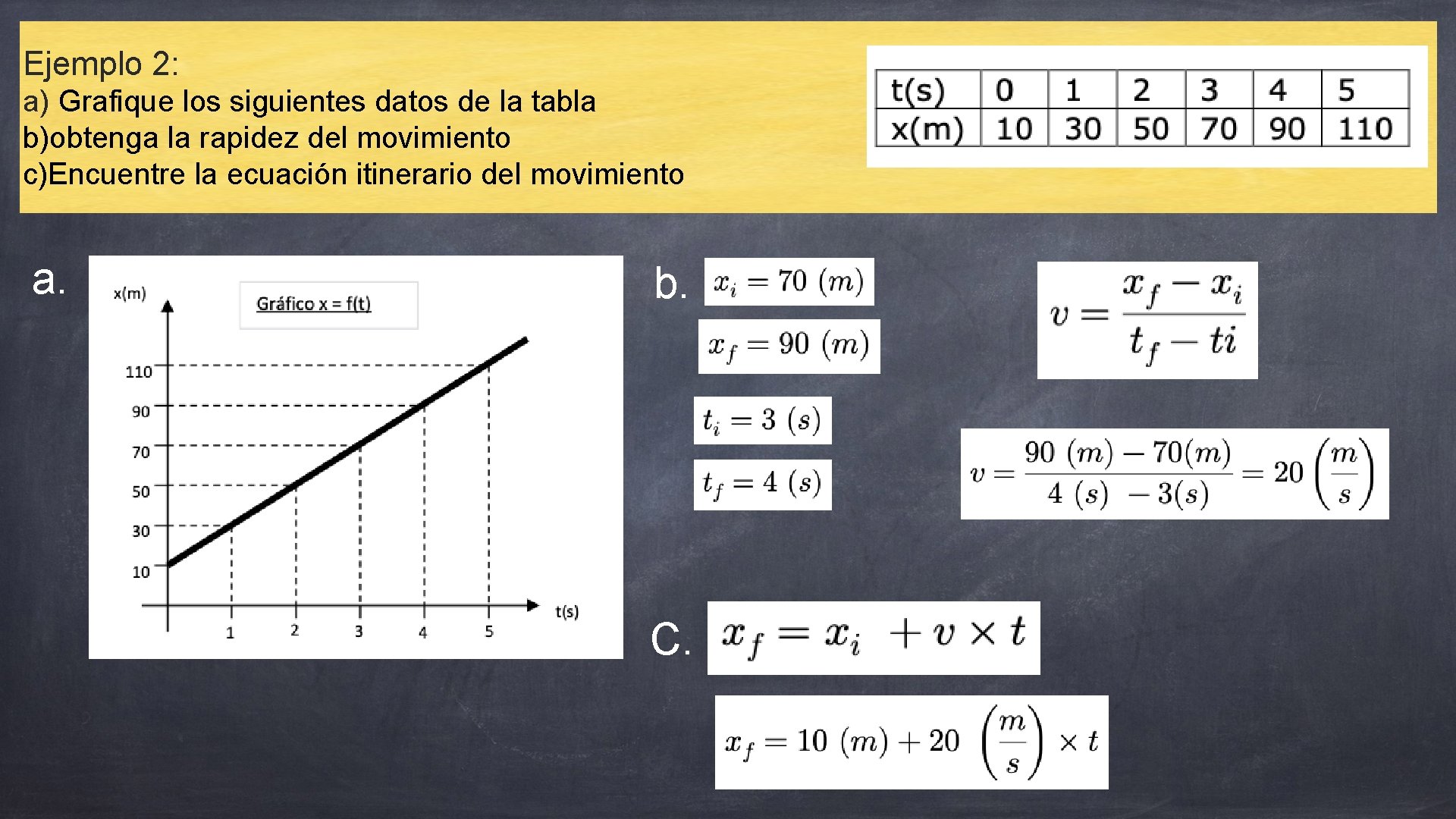
Ejemplo 2: a) Grafique los siguientes datos de la tabla b)obtenga la rapidez del movimiento c)Encuentre la ecuación itinerario del movimiento a. b. C.

Gráfico velocidad en función del tiempo v(t): En un sistema de coordenadas rectangulares se puede representar la velocidad de una partícula en función del tiempo; en el eje horizontal de las abscisas se representa el tiempo y en el eje vertical de las ordenadas se representa la rapidez de la partícula. En el M. R. U. la rapidez es constante por lo tanto la gráfica será la de una función constante, es decir, una recta paralela al eje del tiempo.

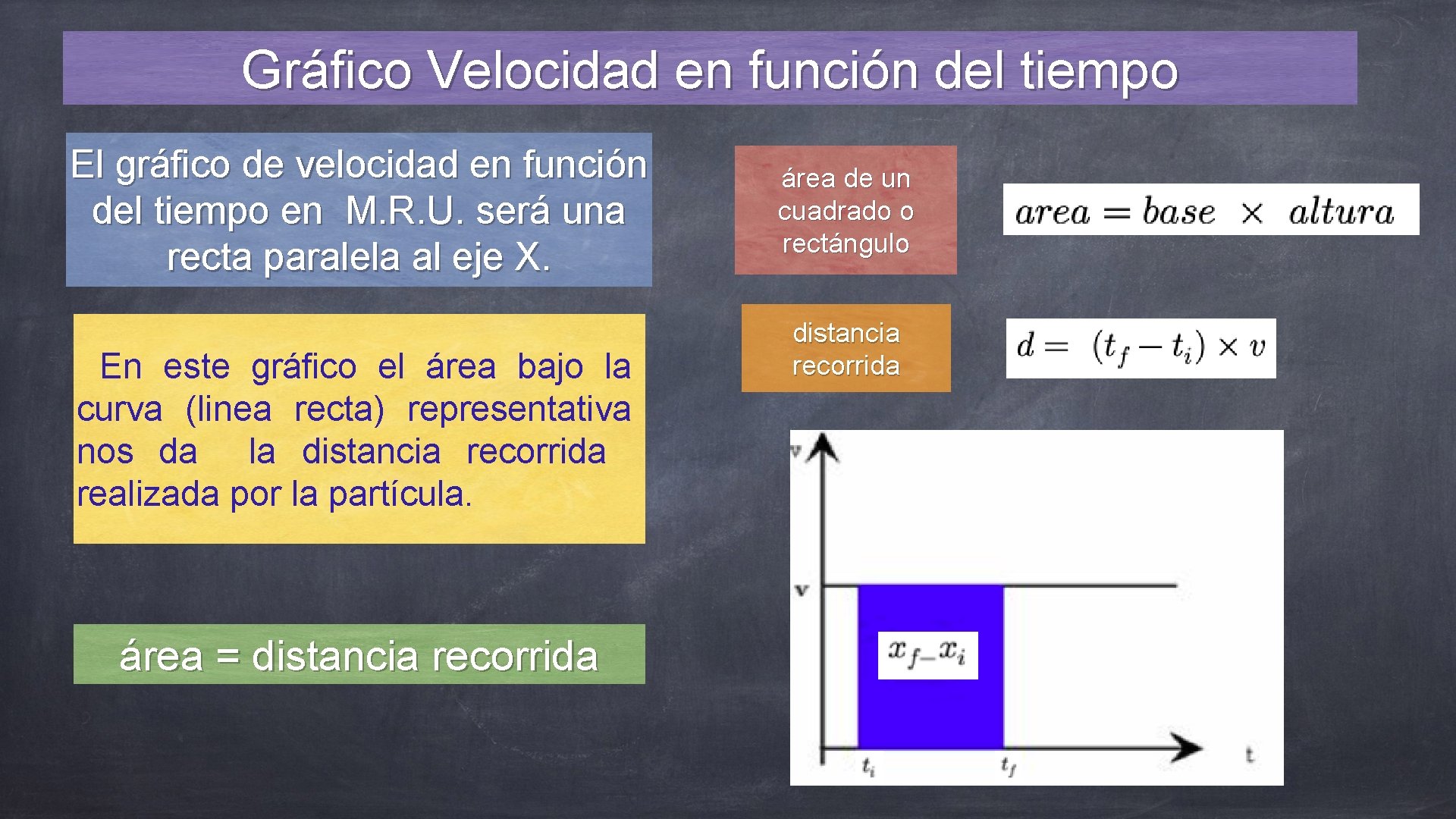
Gráfico Velocidad en función del tiempo El gráfico de velocidad en función del tiempo en M. R. U. será una recta paralela al eje X. En este gráfico el área bajo la curva (linea recta) representativa nos da la distancia recorrida realizada por la partícula. área = distancia recorrida área de un cuadrado o rectángulo distancia recorrida

Ejemplo: Determine la distancia recorrida del móvil en el intervalo de 1 (s) a 7 (s) Consideremos el intervalo de tiempo 1(s) a 7(s) se determinará el área queda encerrada en el intervalo mencionado, la figura que ha formado es un rectángulo cuya base es (tf-ti) y su altura es (v) Entonces el área es: Es decir: El resultado del área bajo la curva de la gráfica v/t corresponde a la distancia recorrida por el móvil en el intervalo de tiempo considerado.

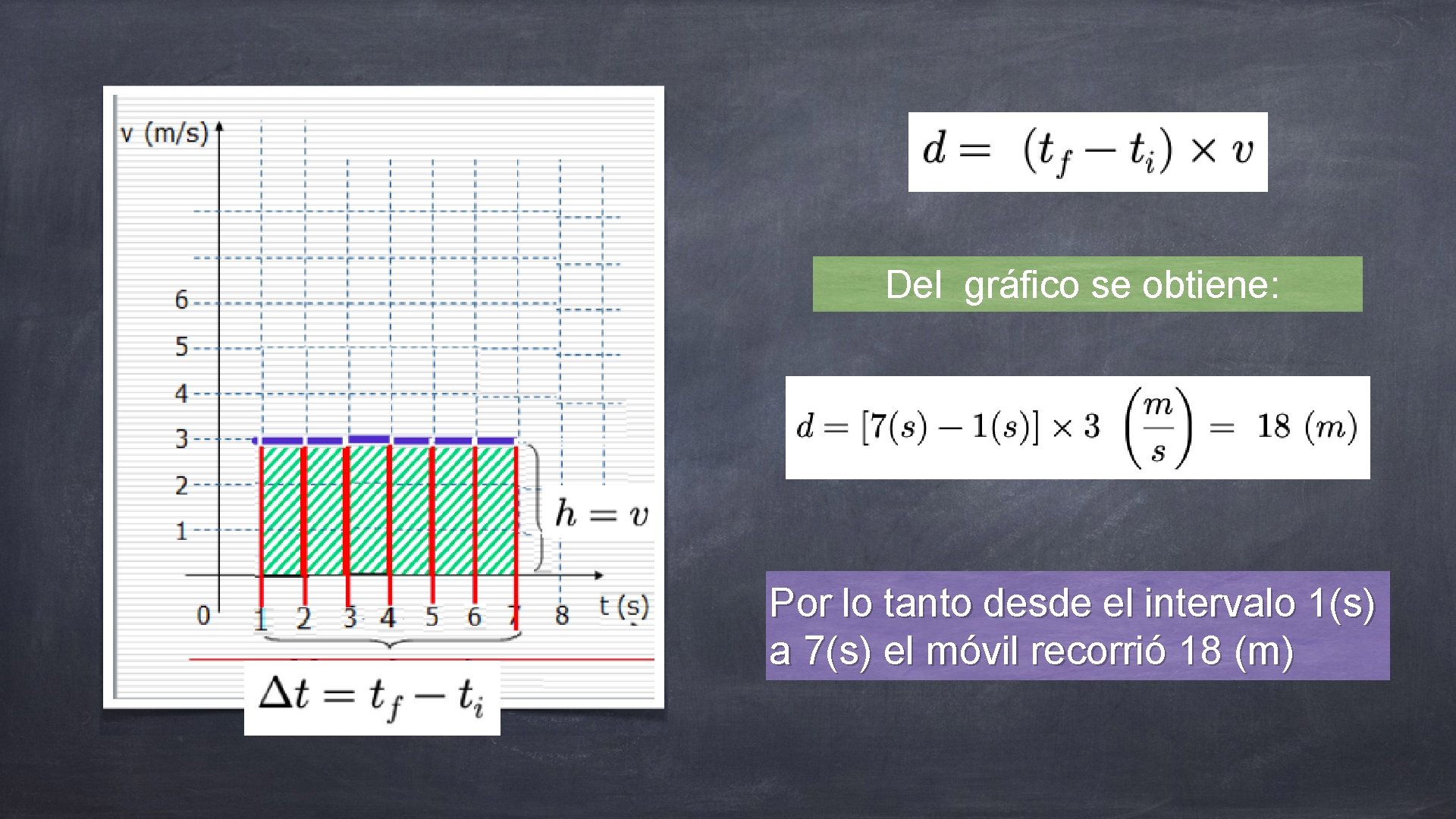
Del gráfico se obtiene: Por lo tanto desde el intervalo 1(s) a 7(s) el móvil recorrió 18 (m)

Realiza el control de salida…