EECS 274 Computer Vision Geometric Camera Models Geometric

EECS 274 Computer Vision Geometric Camera Models

Geometric Camera Models • • Elements of Euclidean geometry Intrinsic camera parameters Extrinsic camera parameters General Form of the Perspective projection equation • Reading: Chapter 2 of FP, Chapter 2 of S

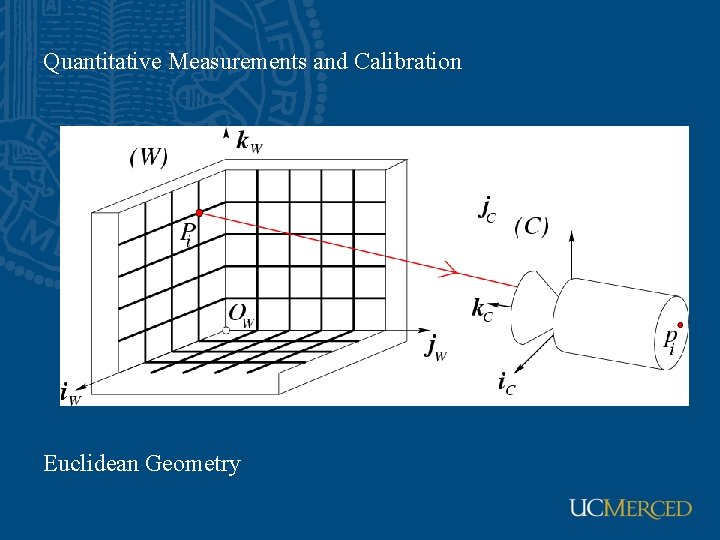
Quantitative Measurements and Calibration Euclidean Geometry

Euclidean Coordinate Systems

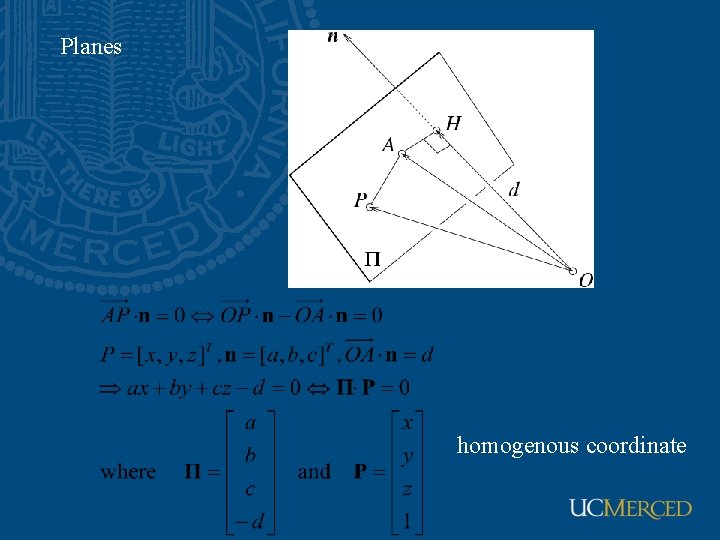
Planes homogenous coordinate

Coordinate Changes: Pure Translations OB P = O B OA + O A P , B P = B OA + A P

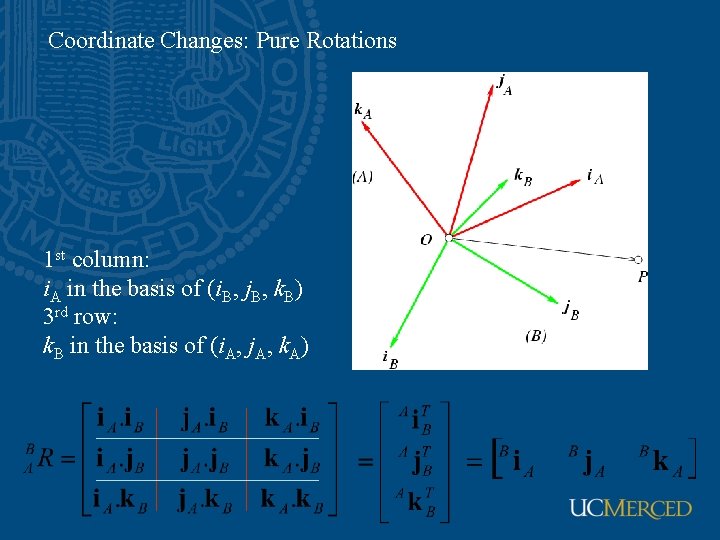
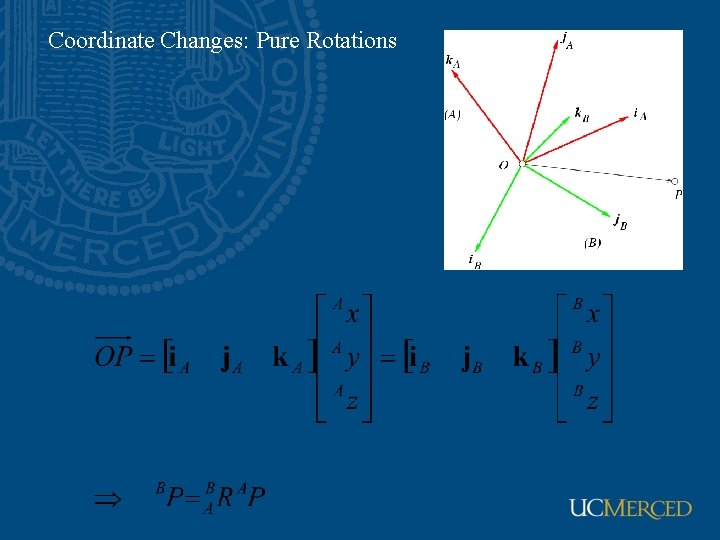
Coordinate Changes: Pure Rotations 1 st column: i. A in the basis of (i. B, j. B, k. B) 3 rd row: k. B in the basis of (i. A, j. A, k. A)

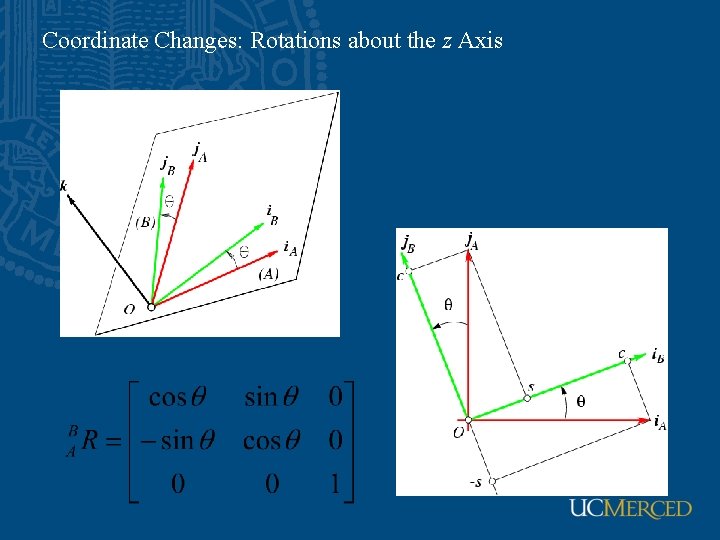
Coordinate Changes: Rotations about the z Axis

Rotation matrix Elementary rotation R=R x R y R z , described by three angles

A rotation matrix is characterized by the following properties: • Its inverse is equal to its transpose, R-1=RT , and • its determinant is equal to 1. Or equivalently: • Its rows (or columns) form a right-handed orthonormal coordinate system.

Rotation group and SO(3) • Rotation group: the set of rotation matrices, with matrix product – Closure, associativity, identity, invertibility • SO(3): the rotation group in Euclidean space R 3 whose determinant is 1 – Preserve length of vectors – Preserve angles between two vectors – Preserve orientation of space

Coordinate Changes: Pure Rotations

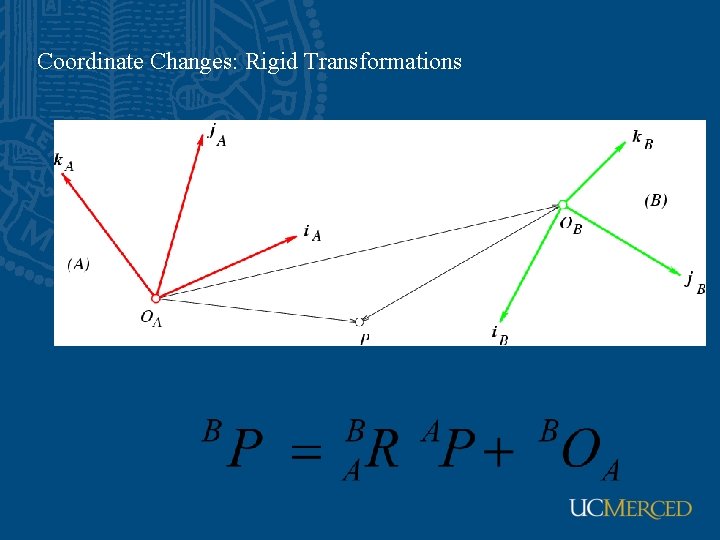
Coordinate Changes: Rigid Transformations

Block Matrix Multiplication What is AB ? Homogeneous Representation of Rigid Transformations

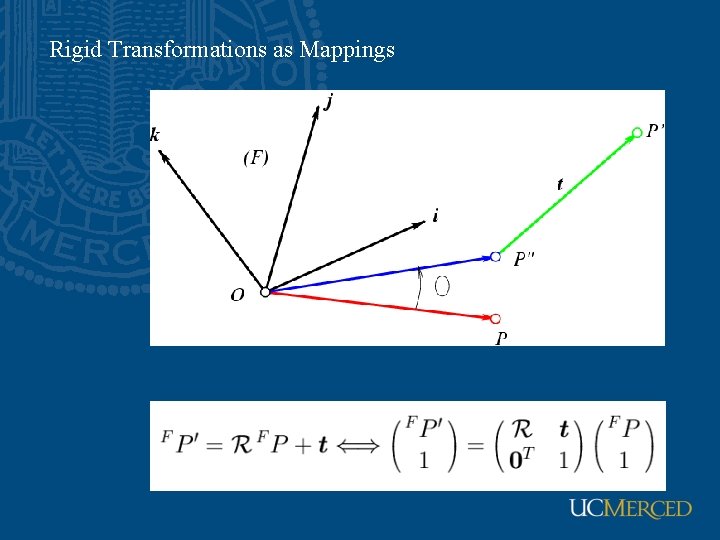
Rigid Transformations as Mappings

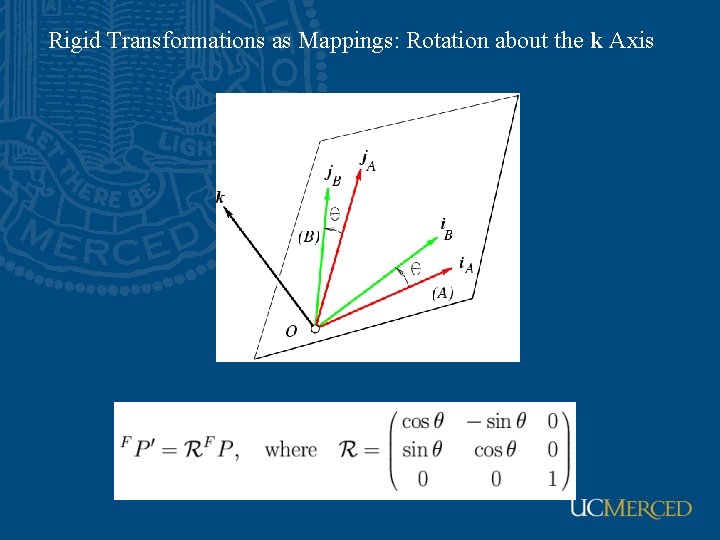
Rigid Transformations as Mappings: Rotation about the k Axis

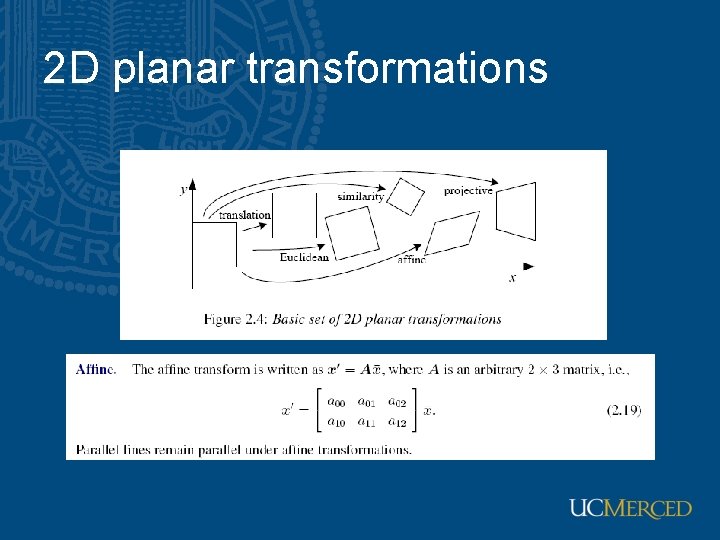
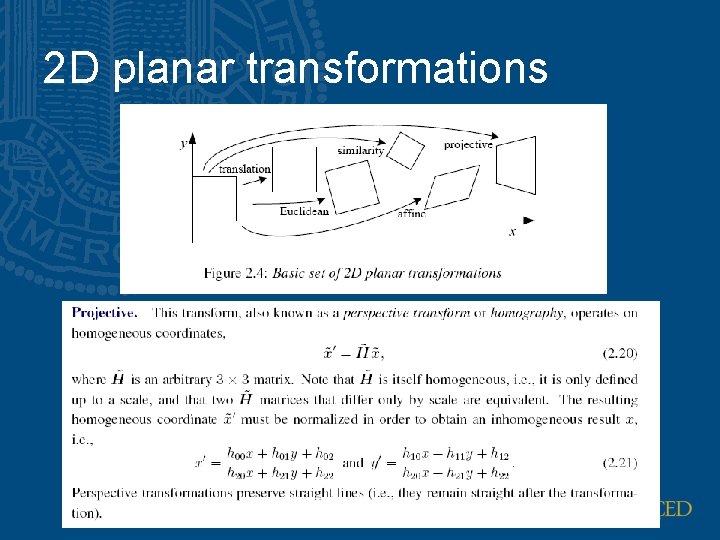
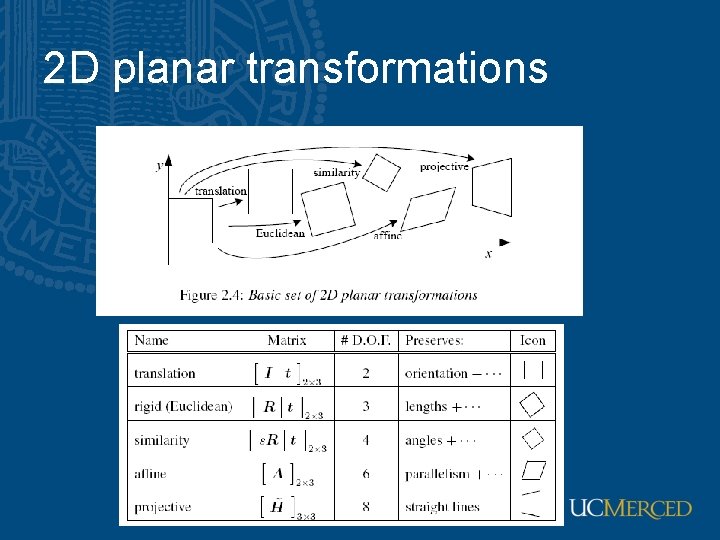
Affine transformation • Images are subject to geometric distortion introduced by perspective projection • Alter the apparent dimensions of the scene geometry

Affine transformation • In Euclidean space, preserve – Collinearity relation between points • 3 points lie on a line continue to be collinear – Ratios of distance along a line • |p 2 -p 1|/|p 3 -p 2| is preserved

Shear matrix Horizontal shear Vertical shear

2 D planar transformations

2 D planar transformations

2 D planar transformations

3 D transformation

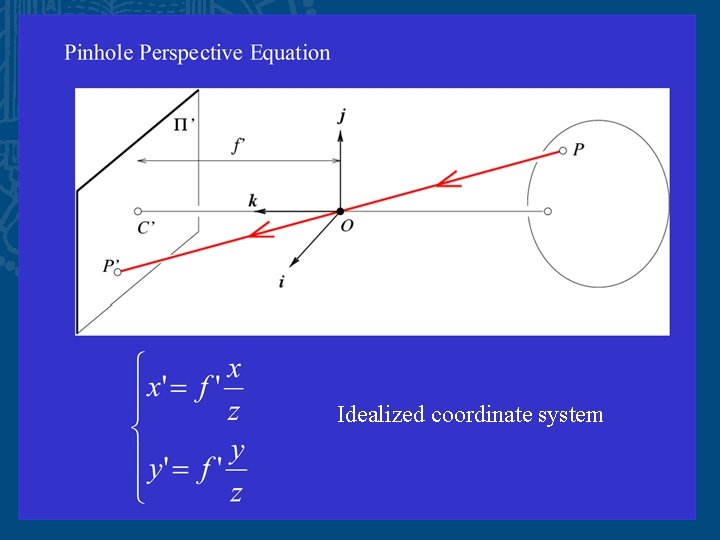
Idealized coordinate system

Camera parameters • Intrinsic: relate camera’s coordinate system to the idealized coordinated system • Extrinsic: relate the camera’s coordinate system to a fix world coordinate system • Ignore the lens and nonlinear aberrations for the moment

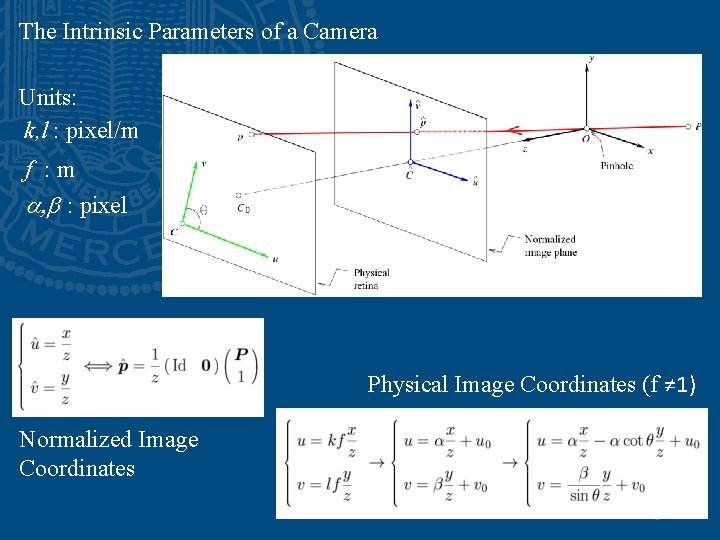
The Intrinsic Parameters of a Camera Units: k, l : pixel/m f : m a, b : pixel Physical Image Coordinates (f ≠ 1) Normalized Image Coordinates

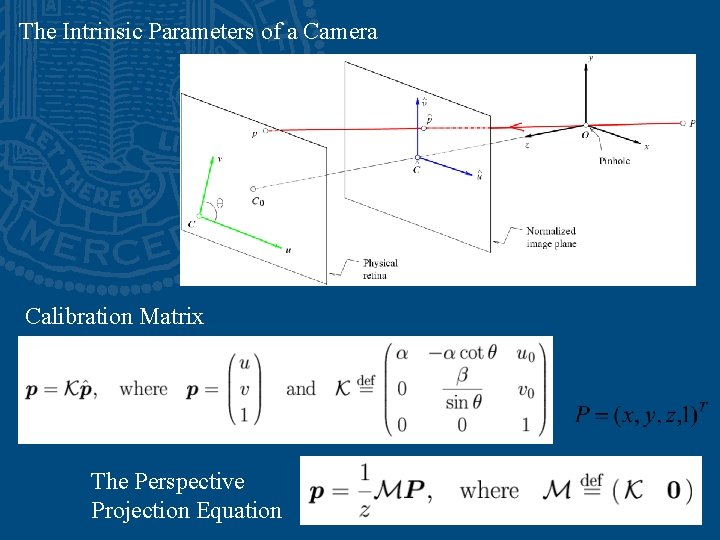
The Intrinsic Parameters of a Camera Calibration Matrix The Perspective Projection Equation

In reality • Physical size of pixel and skew are always fixed for a given camera, and in principal known during manufacturing • Focal length may vary for zoom lenses • Optical axis may not be perpendicular to image plane • Change focus affects the magnification factor • From now on, assume camera is focused at infinity

Extrinsic Parameters

Explicit Form of the Projection Matrix denotes the i-th row of R, tx, ty, tz, are the coordinates of t can be written in terms of the corresponding angles R can be written as a product of three elementary rotations, and described by three angles M is 3 x 4 matrix with 11 parameters 5 intrinsic parameters: α, β, u 0, v 0, θ 6 extrinsic parameters: 3 angles defining R and 3 for t

Explicit Form of the Projection Matrix Note: M is only defined up to scale in this setting!! : i-th row of R

Theorem (Faugeras, 1993)

Camera parameters A camera is described by several parameters • • • Translation T of the optical center from the origin of world coords Rotation R of the image plane focal length f, principle point (x’c, y’c), pixel size (sx, sy) • blue parameters are called “extrinsics, ” red are “intrinsics” Projection equation • • The projection matrix models the cumulative effect of all parameters Useful to decompose into a series of operations identity matrix intrinsics • projection rotation translation Definitions are not completely standardized – especially intrinsics—varies from one book to another