Dynamics in a model for quantum measurements and

Dynamics in a model for quantum measurements and insights in the Quantum Measurement Problem Theo M. Nieuwenhuizen CCPP, NYU & ITP, Univ. of Amsterdam Armen Allahverdyan, Yerevan Roger Balian, Saclay Europhysics Letters 2003 ar. Xiv 2004, Vaxjo 2005, 2006 Beyond the Quantum 2007 ar. Xiv 2008 Opus Magnum, in progress 155 pages, Physics Reports Foundations of Probability and Physics -6 Linneus University, Vaxjo, 16 -6, 2011

Setup Statistical interpretation of QM Problems & paradoxes + the big questions The model: system S + apparatus A spin-½ A = M + B = magnet + bath Selection of collapse basis & fate of Schrodinger cats Registration of the Q-measurement & classical measurement Post measurement & the Born rule The Q measurement problem elucidated Summary

Statistical interpretation of QM Density matrix describes ensemble of identically prepared systems Pure state is limiting case; same meaning (no special role) Ensemble can be real: (many particles: bundle at LHC one trapped ion in photon field, repeated excitation) or virtual: (as in classical statistical physics) QM = tool for calculating averages from density matrix ρ => QM = about what we can measure, not about what is epistomology ontology Quantum measurement theory describes ensemble of measurements on ensemble of identically prepared systems

Problems & paradoxes Einstein, Bohr, de Broglie, von Neumann, Wigner, Bohm, Bell, Balian, van Kampen. . . Collapse = non-unitary Small part of apparatus described by QM why not measurement process? Preferred basis paradox: on which basis will reduction take place? When does collapse happen ? How long does it take? What happens to Schrödinger cats? The biggest of them all: The quantum measurement problem: QM = statistical theory, but in experiments we see individual outcomes Solvable within QM ? ? => probably not …or? ?

Requirements for Q measurement models R 1: simulate as much as possible real experiments; R 2: ensure unbiased, robust, permanent registration by macroscopic pointer R 3: to amplify quantum signal: involve an apparatus initially in a metastable state and evolving towards one of the stable states under the influence of S; the transition of A, instead of occurring spontaneously, is triggered by S; R 4: include a bath where the free energy may be dumped; R 5: be solvable so as to provide a complete scenario of the joint evolution of S + A and to exhibit the characteristic times; R 6: conserve the tested observable; R 7: lead to a final state devoid of “Schrodinger cats”; R 8: satisfy Born’s rule for the registered results; R 9: produce, for ideal measurements or preparations, the required diagonal correlations between the tested system and the indication of the pointer, R 10: be su�ciently flexible to allow discussing imperfect measurements.

Curie-Weiss model for quantum measurements System S: s = spin-½. For ideal measurement: Apparatus = Magnet + Bath (A = M + B). M = N spins-½ σ(n). Pointer = magnetization B = phonon bath: harmonic oscillators

Spin-spin interactions in magnet M • J 2 term: Curie-Weiss magnet • J 4 term: allows first order phase transition • Extreme case of first order transition: J 2 = 0, J 4 = J

Bath Hamiltonian Standard harmonic oscillator bath: x, y, z components of the spins of M couple to their own harmonic oscillators Bath characterized by correlator K(t-t’) Weak M-B coupling: γ << 1 allows to work at lowest order in γ

Initial density matrix Tested system S: arbitrary density matrix uncorrelated with A Apparatus A starts in mixed state, (large system cannot be prepared in pure state) Magnet M: N spins ½, starts as paramagnet (mixed state) Bath: Gibbs state (mixed state) β = 1/T Apparatus starts in mixed state => system may end up in mixed state No unitarity paradox

Selection of collapse basis What selects collapse basis? The interaction Hamiltonian ! Liouville-von Neumann eqn The 4 sectors decouple ideality of the measurement Motion of the spin a=z: Diagonal terms of r(t) conserved ->= rii(t) = rii(0 ): Born probabilities a=x, y: Off-diagonal terms evolve => disappearence of Schrodinger cats

Fate of Schrodinger cat terms Short times: spin-spin couplings in magnet are irrelevant x, y components of spin n of M moves in the magnetic field g of spin S Larmor procession damping by zero-point flucts of bath Schrodinger cat: dephasing decoherence as in NMR comes in later Recurrences eliminated by: decoherence by bath N B >> 1 or even by a spread in g’s Creation of multi-particle correlations: weak, dying out Schrodinger cat terms die quickly in cascade of weak multi-spin correlations

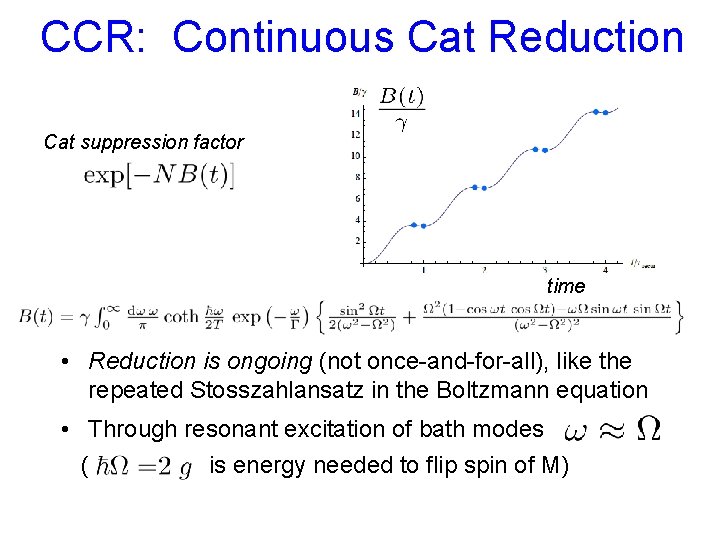
CCR: Continuous Cat Reduction Cat suppression factor time • Reduction is ongoing (not once-and-for-all), like the repeated Stosszahlansatz in the Boltzmann equation • Through resonant excitation of bath modes ( is energy needed to flip spin of M)

Registration of the measurement Solve Q-dynamics of diagonal elements to second order in the coupling to bath In sector with sz =1: analogy to classical measurement of classical Ising spin sz =1 Magnetization m involves only eigenvalues , as in classical statistical physics Measure a spin with a “classical” apparatus of magnet and a bath Dynamics Free energy F=U-TS: minima are stable states of free energy m

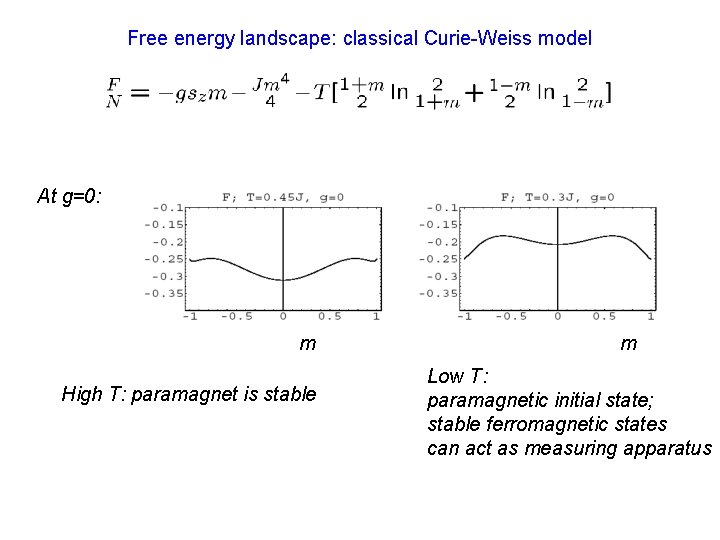
Free energy landscape: classical Curie-Weiss model At g=0: m High T: paramagnet is stable m Low T: paramagnetic initial state; stable ferromagnetic states can act as measuring apparatus

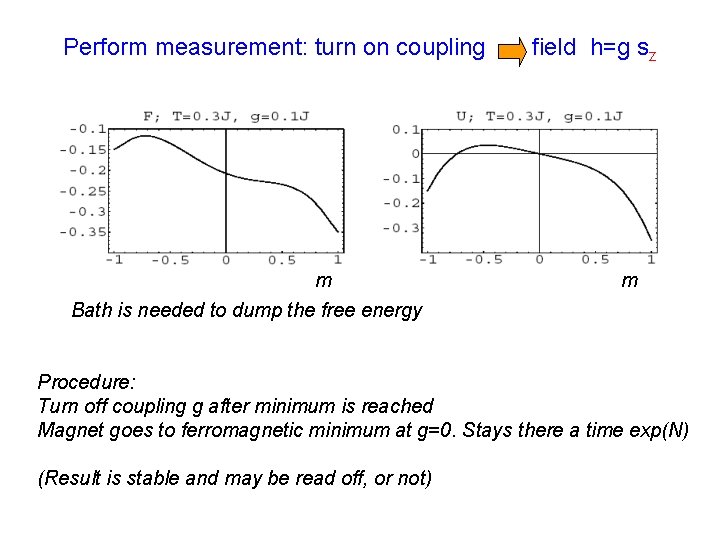
Perform measurement: turn on coupling field h=g sz m Bath is needed to dump the free energy m Procedure: Turn off coupling g after minimum is reached Magnet goes to ferromagnetic minimum at g=0. Stays there a time exp(N) (Result is stable and may be read off, or not)

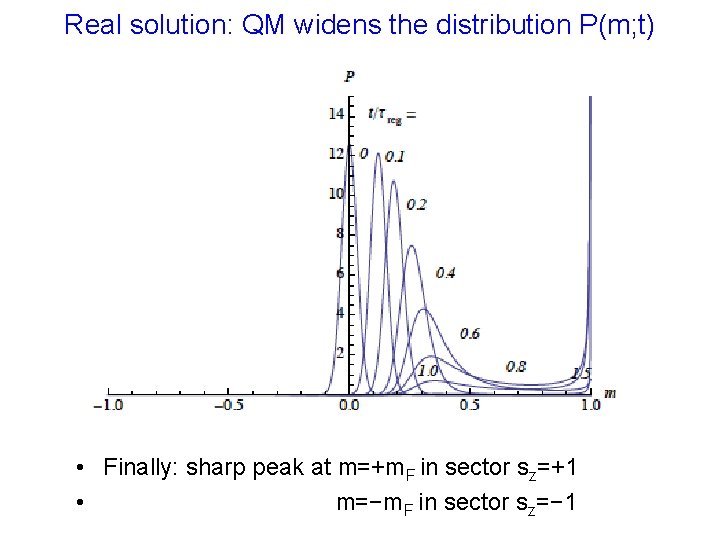
Real solution: QM widens the distribution P(m; t) • Finally: sharp peak at m=+m. F in sector sz=+1 • m=−m F in sector sz=− 1

Post-measurement state Magnet ends up in up/down ferromagnetic state Sign of magnetization maximally correlated with sign spin S Probabilities satisfy Born rule No Schrodinger cat terms Physical disappearance: sums of many oscillating terms vanish despite of mathematical survival: individual terms have fixed amplitude

On the Quantum Measurement Problem The macroscopic magnet itself is well understood. Initial paramagnet relaxes to stable or ferromagnet Ensemble theory describes breaking of ergodicity Individual and ferromaget is stable, Poincare time is very large In Q measurement this transition is triggered by coupling to the spin S Long life time of FM state ensures uniqueness of outcome for m=±m. F and for the measured spin sz = ± 1 that is fully correlated with it No survival of Schrodinger cat terms, that could spoil this view. One may select individual outcomes with magnetization (possible because ferromagnetic state longlived) This unambiguous subensemble is a pure ensemble of spins of S

Summary: the measurement problem elucidated • Collapse basis determined by interaction Hamiltonian • Measurement in two steps: cats die & registration of the result very fast is slower cascade of small multi-particle correlations ongoing reduction • Registration : some classical features ( Bohr) macroscopic pointer: irreversible dynamics, entropy increase • Born rule results from the dynamics • Observation of pointer is irrelevant for outcomes ( Wigner) (results may be read off, or processed automatically) • Statistical interpretation of QM • Individual outcomes due to irreversible phase transition in magnet long lived pointer indication, no cat terms

How to teach QM • Copenhagen interpretation • Statistical interpretation: minimalistic, simple

On the interpretation of QM Statistical interpretation: QM describes ensembles, not single systems Q-measurement theory = about ensembles of measurements Solution gives probabilities for outcomes of experiments: system in collapsed state + apparatus in pointer state Density matrix describes my knowledge about the ensemble of identically prepared systems Should be updated after measurement

Statistical interpretation of QM Einstein again wrote on it even in 1955 Kemble : in his book 1937 Ballentine: Rev Mod Phys 1975 van Kampen: Am J Phys 1988 Balian: Am J Phys 1989 Statistical interpretation: a density matrix (mixed or pure) describes an ensemble of systems Stern-Gerlach expt: ensemble of particles in upper beam described by |up> Q-measurement theory describes the statistics of outcomes of an ensemble of measurements on an ensemble of systems

Quantum Mechanics is a theory that describes the statistics of outcomes of experiments It cannot and should not describe individual experiments (otherwise than in a probablistic sense)

The Quantum measurement problem • Why do we see individual outcomes in individual measurements? • Perhaps because there is an underlying reality in which the events occur (“world”, “nature”, “life”)? • Should there exist a theory for that? Hidden-variables theory, sub-quantum mechanics

Other interpretations • Copenhagen: each system has its own wavefunction, that has the most complete info in a statistical sense. There is an underlying wavefunction of system + apparatus • Ghirardi-Rimini-Weber GRW: collapse is a physical process, modification of QM needed to achieve the collapses. • Multi-universe: at each measurement one of the branches is chosen, other ones in other universes. • Wigner’s friend: the observer “finishes” the measurement • Decoherence picture: pointer is a mode of the bath (The air measures my height)

The Born rule as an identification at the macroscopic level In practice: describes statistics of pointer states determine relative frequencies (von Mises) Post-measurement state of tested system is a mixed state,