Quantum dynamics and quantum control of spins in

Quantum dynamics and quantum control of spins in diamond Viatcheslav Dobrovitski Ames Laboratory US DOE, Iowa State University Works done in collaboration with Z. H. Wang (Ames Lab – now USC), T. der Sar, G. de Lange, T. Taminiau, R. Hanson (TU Delft), G. D. Fuchs, D. Toyli, D. D. Awschalom (UCSB), D. Lidar (USC)

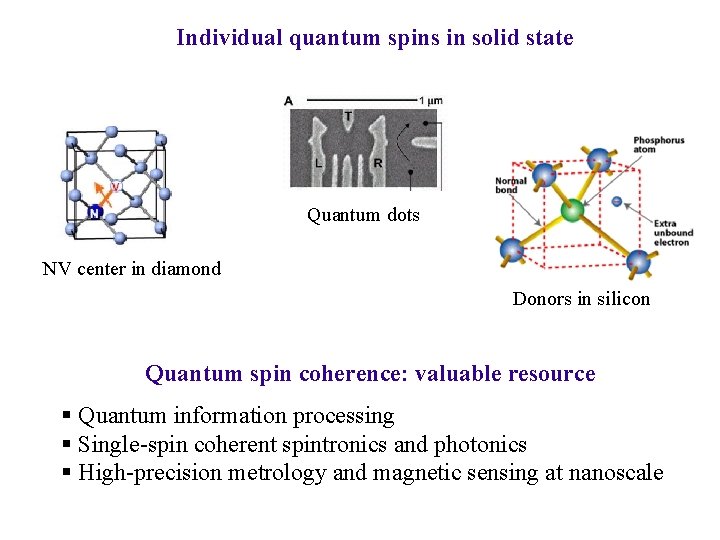
Individual quantum spins in solid state Quantum dots NV center in diamond Donors in silicon Quantum spin coherence: valuable resource § Quantum information processing § Single-spin coherent spintronics and photonics § High-precision metrology and magnetic sensing at nanoscale

Grand challenge – controlling single quantum spins in solids Fundamental problems: 1. Understand dynamics of individual quantum spins 2. Control individual quantum spins 3. Preserve coherence of quantum spins 4. Generate and preserve entanglement between quantum spins Spins in diamond – excellent testbed for quantum studies • Long coherence time • Individually addressable • Controllable optically and magnetically Jelezko et al, PRL 2004; Gaebel et al, Nat. Phys. 2006; Childress et al, Science 2006

Dynamical decoupling protocols Traditional analysis and classification: Magnus expansion Simplest – Periodic DD : Symmetrized protocol: Period τ -X- τ -X τ-X-X- τ = τ -X- τ CPMG sequence 2 nd order protocol, error O(τ2) Concatenated protocols (CDD) level l=1 (CDD 1 = PDD): τ -X- τ -X level l=2 (CDD 2): etc. PDD-X-PDD-X

Deficiencies of Magnus expansion: • Norm of H(0), H(1), … – grows with the size of the bath • Validity conditions are often not satisfied in reality (the UV cutoff is too large) but DD works • Behavior at long times – unclear • Accumulation of pulse errors and imperfections – unknown Assessing the quality of coherence protection 1. Exact numerical modeling Up to 32 spins (Hilbert space d = 4× 109) on 128 processors Parallel code, 80 % efficiency 2. Approximate – but very accurate – numerics: coherent spin states 3. Analytical mean-field techniques

Outline 1. Quantum control and dynamical decoupling of NV center: 2. protecting coherence Spectacular recent progress: DD on a single NV spin de Lange, Wang, Riste, Dobrovitski, Hanson: Science 2010 Ryan, Hodges, Cory: PRL 2010 Naydenov, Dolde, Hall, Fedder, Hollenberg, Jelezko, Wrachtrup: PRB 2010 2. Decoherence-protected quantum gates 3. Decoherence-protected quantum algorithm: first 2 -qubit computation with invidivual solid-state spins

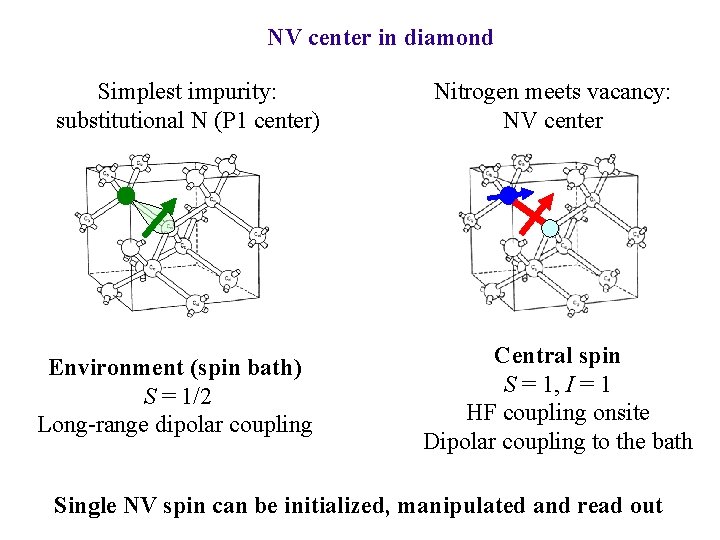
NV center in diamond Simplest impurity: substitutional N (P 1 center) Environment (spin bath) S = 1/2 Long-range dipolar coupling Nitrogen meets vacancy: NV center Central spin S = 1, I = 1 HF coupling onsite Dipolar coupling to the bath Single NV spin can be initialized, manipulated and read out

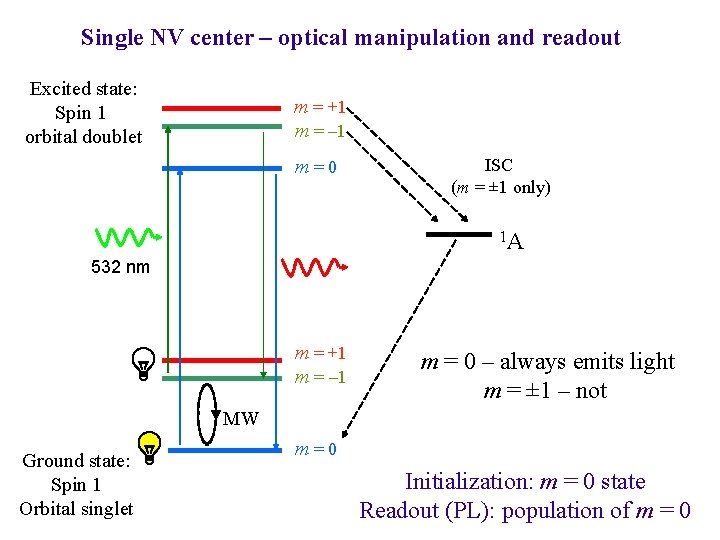
Single NV center – optical manipulation and readout Excited state: Spin 1 orbital doublet m = +1 m = – 1 m=0 ISC (m = ± 1 only) 1 A 532 nm m = +1 m = – 1 m = 0 – always emits light m = ± 1 – not MW Ground state: Spin 1 Orbital singlet m=0 Initialization: m = 0 state Readout (PL): population of m = 0

Decoherence: NV center in a spin bath NV spin C C N V C C C Bath spin – N atom ms = – 1 C ms = +1 m = +1/2 ms = -1/2 ms = 0 B NV electron spin: pseudospin S = 1/2 (qubit) No flip-flops between NV and the bath: energy mismatch – field created by the bath spins Time dependence governed by HB B

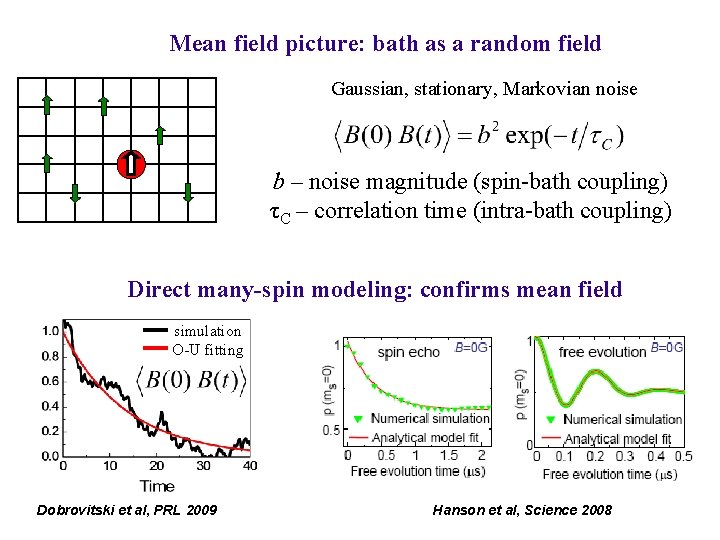
Mean field picture: bath as a random field Gaussian, stationary, Markovian noise b – noise magnitude (spin-bath coupling) τC – correlation time (intra-bath coupling) Direct many-spin modeling: confirms mean field simulation O-U fitting Dobrovitski et al, PRL 2009 Hanson et al, Science 2008

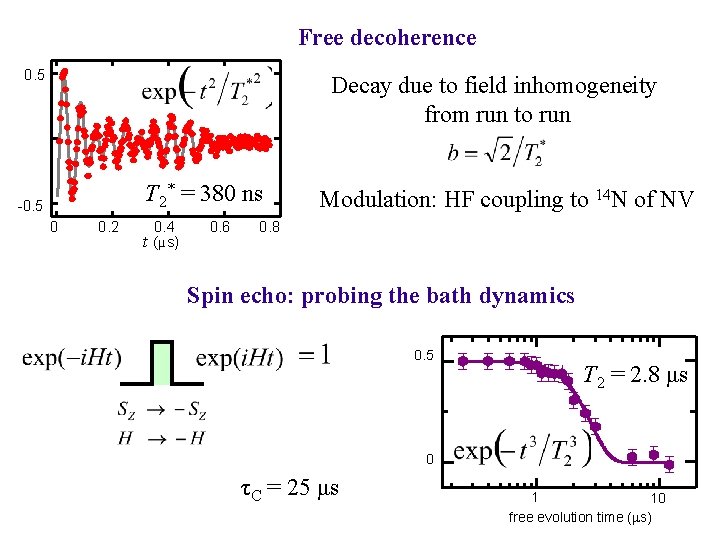
Free decoherence 0. 5 Decay due to field inhomogeneity from run to run T 2* = 380 ns -0. 5 0 0. 2 0. 4 t (µs) 0. 6 Modulation: HF coupling to 14 N of NV 0. 8 Spin echo: probing the bath dynamics 0. 5 T 2 = 2. 8 μs 0 τC = 25 μs 1 10 free evolution time (ms)

Quantum control and Dynamical decoupling: Extending coherence time of a single NV center

Choice of the DD protocol: theory Short times (T << τC): PDD Long times (T >> τC): τ -X- τ -X Fast decay CPMG Slow decay at all times, rate τ-X- 2τ -X-τ Slow decay WS (T) optimal choice Concatenated PDD Fast decay at all times, makes things worse Concatenated CPMG Slow decay at all times, no improvement and many other protocols have been analyzed…

Qualitative features • Coherence time can be extended well beyond τC as long as the inter-pulse interval is small enough: τ/τC << 1 • Magnus expansion (also similar cumulant expansions) predict: W(T) ~ O(N τ4) for PDD but we have W(T) ~ O(N τ3) Symmetrization or concatenation give no improvement Source of disagreement: Magnus expansion is inapplicable Ornstein-Uhlenbeck noise: Second moment is (formally) infinite – corresponds to Cutoff of the Lorentzian:

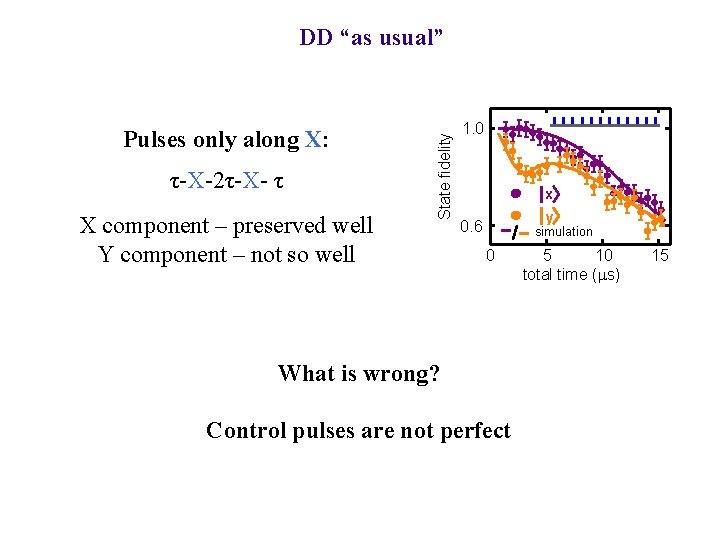
Pulses only along X: τ-X-2τ-X- τ X component – preserved well Y component – not so well State fidelity DD “as usual” 1. 0 x y 0. 6 simulation 0 What is wrong? Control pulses are not perfect 5 10 total time (ms) 15

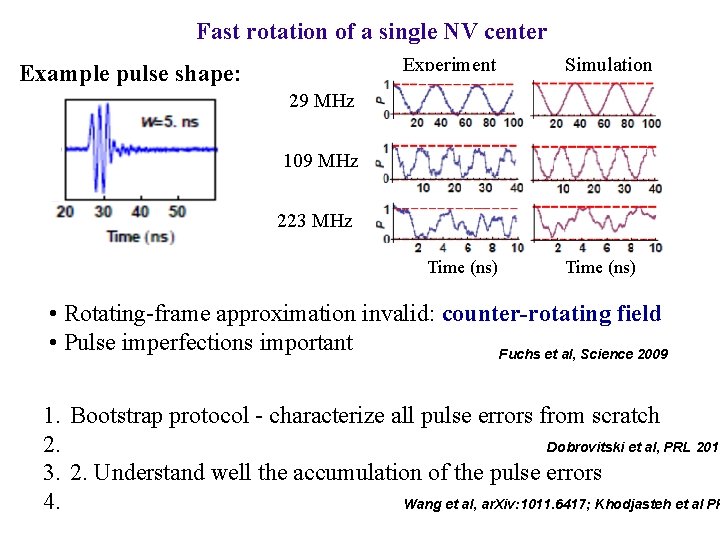
Fast rotation of a single NV center Experiment Example pulse shape: Simulation 29 MHz 109 MHz 223 MHz Time (ns) • Rotating-frame approximation invalid: counter-rotating field • Pulse imperfections important Fuchs et al, Science 2009 1. Bootstrap protocol - characterize all pulse errors from scratch 2. Dobrovitski et al, PRL 2010 3. 2. Understand well the accumulation of the pulse errors 4. Wang et al, ar. Xiv: 1011. 6417; Khodjasteh et al PR

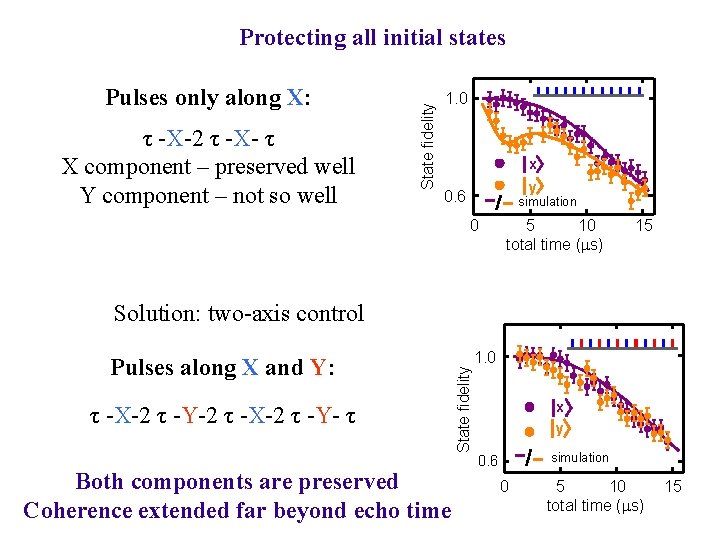
Pulses only along X: τ -X-2 τ -X- τ X component – preserved well Y component – not so well State fidelity Protecting all initial states 1. 0 x y 0. 6 simulation 0 5 10 total time (ms) 15 Pulses along X and Y: τ -X-2 τ -Y-2 τ -X-2 τ -Y- τ Both components are preserved Coherence extended far beyond echo time State fidelity Solution: two-axis control 1. 0 x y simulation 0. 6 0 5 10 total time (ms) 15

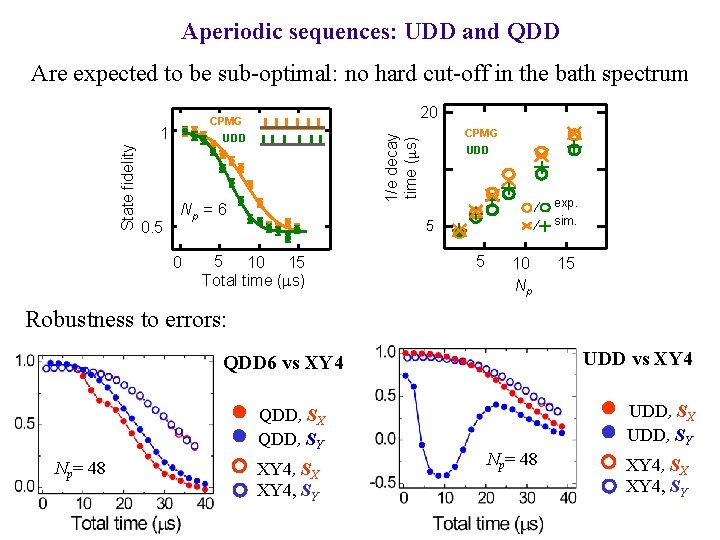
Aperiodic sequences: UDD and QDD Are expected to be sub-optimal: no hard cut-off in the bath spectrum UDD Np = 6 0 CPMG 1/e decay time (μs) State fidelity 1 0. 5 20 CPMG UDD exp. sim. 5 5 10 15 Total time (ms) 5 10 Np 15 Robustness to errors: UDD vs XY 4 QDD 6 vs XY 4 QDD, SX QDD, SY Np= 48 XY 4, SX XY 4, SY UDD, SX UDD, SY Np= 48 XY 4, SX XY 4, SY

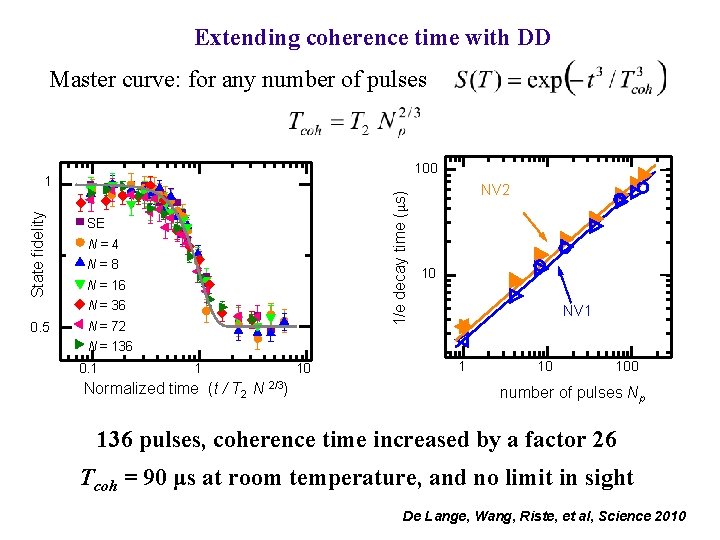
Extending coherence time with DD Master curve: for any number of pulses 100 1/e decay time (μs) State fidelity 1 SE N=4 N=8 N = 16 N = 36 0. 5 N = 72 NV 2 10 NV 1 N = 136 0. 1 1 Normalized time (t / T 2 N 2/3) 10 100 number of pulses Np 136 pulses, coherence time increased by a factor 26 Tcoh = 90 μs at room temperature, and no limit in sight De Lange, Wang, Riste, et al, Science 2010

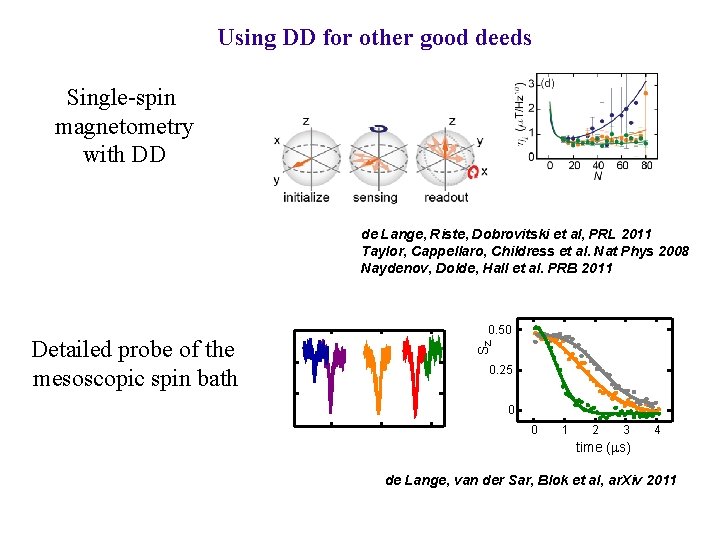
Using DD for other good deeds Single-spin magnetometry with DD de Lange, Riste, Dobrovitski et al, PRL 2011 Taylor, Cappellaro, Childress et al. Nat Phys 2008 Naydenov, Dolde, Hall et al. PRB 2011 SZ Detailed probe of the mesoscopic spin bath 0. 50 0. 25 0 0 1 2 3 4 time (ms) de Lange, van der Sar, Blok et al, ar. Xiv 2011

Combining DD and quantum operation Gates with resonant decoupling

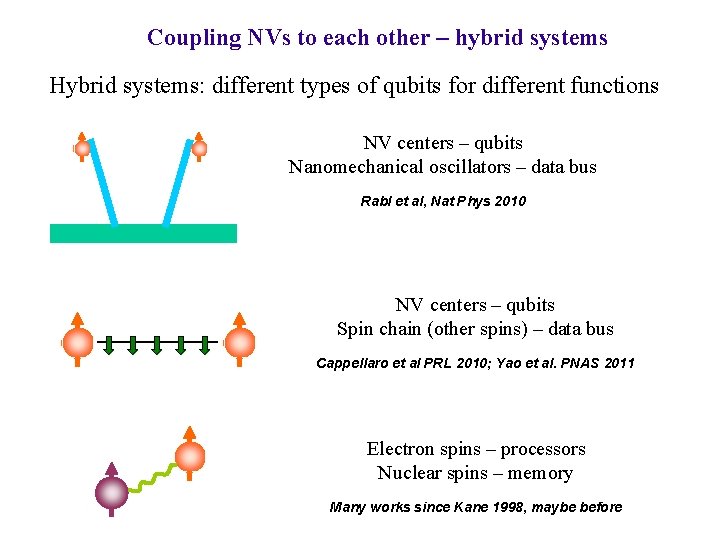
Coupling NVs to each other – hybrid systems Hybrid systems: different types of qubits for different functions NV centers – qubits Nanomechanical oscillators – data bus Rabl et al, Nat Phys 2010 NV centers – qubits Spin chain (other spins) – data bus Cappellaro et al PRL 2010; Yao et al. PNAS 2011 Electron spins – processors Nuclear spins – memory Many works since Kane 1998, maybe before

“Standard” quantum operation Unprotected quantum gate Bath Protected storage: decoupling Bath Contradiction: DD efficiently preserves the qubit state but quantum computation must change it

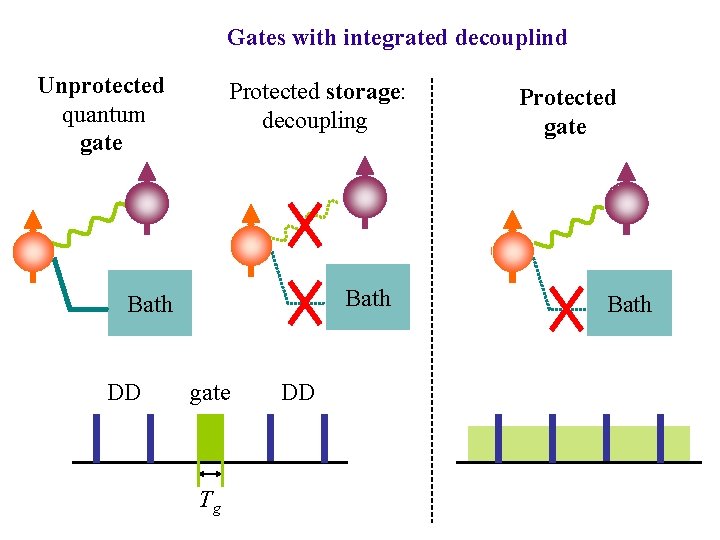
Gates with integrated decouplind Unprotected quantum gate Protected storage: decoupling Bath DD gate Tg DD Protected gate Bath

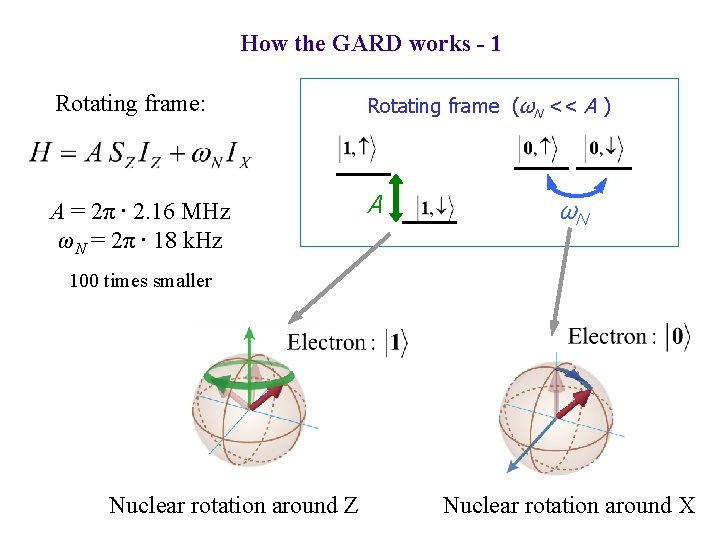
Gate with resonant decoupling (GARD) for hybrid systems Different qubits have different coherence and control timescales One qubits decoheres before another starts to move Nuclear 14 N spin: memory, Electronic NV spin: processing (quantum memory, quantum repeater, magnetic sensing, etc. ) Childress, Taylor, Sorensen et al. PRL 2006 Taylor, Marcus, Lukin PRL 2003 Jiang, Hodges, Maze et al. Science 2009 Neumann, Beck, Steiner et al. Science 2011 C C N V C C C But control of nuclear spin takes much longer than T 2* C Poor choice: either decouple the electron – no gates possible or gating without DD – no gates possible A way out: use internal resonance in the system

How the GARD works - 1 Rotating frame: Rotating frame (ωN << A ) A = 2π ∙ 2. 16 MHz ωN = 2π ∙ 18 k. Hz A ωN 100 times smaller Nuclear rotation around Z Nuclear rotation around X

How the GARD works - 2 Main problem: electron switches very frequently between 0 and 1 and slow nuclear spin should keep track of this Contradiction with the very idea of DD? Motion of the nuclear spin: conditional single-spin rotation XY 4 unit: τ -X- τ -Y- τ 0 -X-1 -1 -Y-0 1 -X-0 -0 -Y-1 Axes n 0 and n 1 are both close to z (A >> ω1): small Resonance: smth 2 also becomes small when

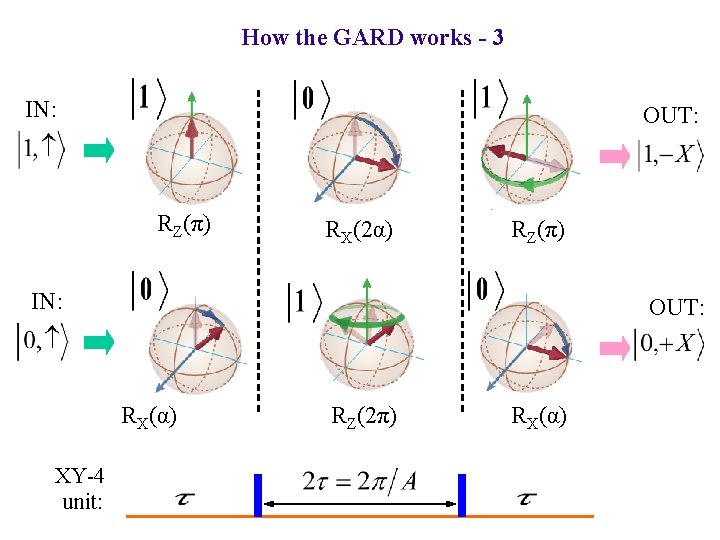
How the GARD works - 3 IN: OUT: RZ(π) RX(2α) RZ(π) IN: OUT: RX(α) XY-4 unit: RZ(2π) RX(α)

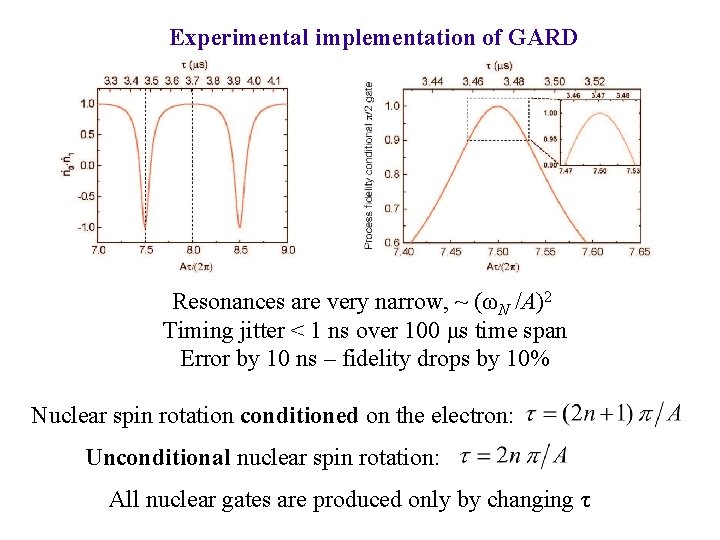
Experimental implementation of GARD Resonances are very narrow, ~ (ωN /A)2 Timing jitter < 1 ns over 100 μs time span Error by 10 ns – fidelity drops by 10% Nuclear spin rotation conditioned on the electron: Unconditional nuclear spin rotation: All nuclear gates are produced only by changing τ

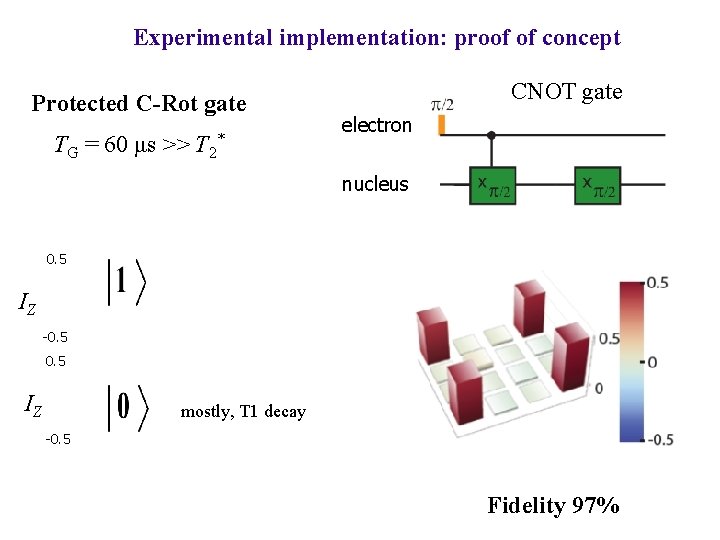
Experimental implementation: proof of concept Protected C-Rot gate TG = 60 μs >> T 2* CNOT gate electron nucleus 0. 5 IZ -0. 5 IZ mostly, T 1 decay -0. 5 Fidelity 97%

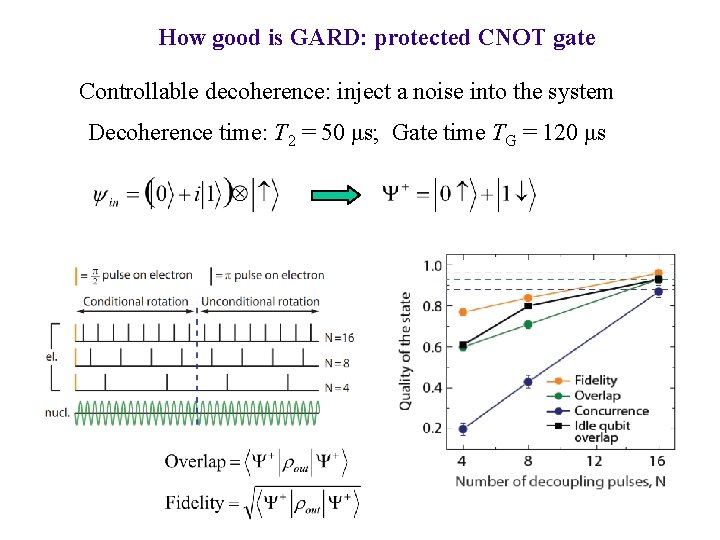
How good is GARD: protected CNOT gate Controllable decoherence: inject a noise into the system Decoherence time: T 2 = 50 μs; Gate time TG = 120 μs

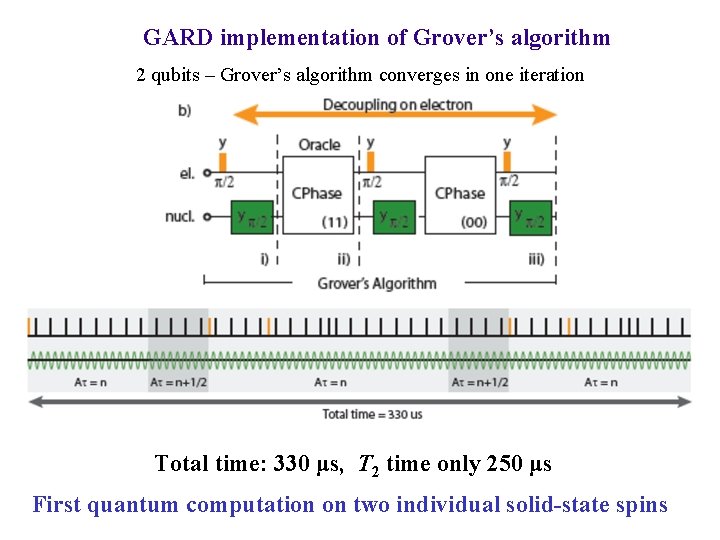
GARD implementation of Grover’s algorithm 2 qubits – Grover’s algorithm converges in one iteration Total time: 330 μs, T 2 time only 250 μs First quantum computation on two individual solid-state spins

GARD implementation of Grover’s algorithm 1 2 3 4 5 6 Fidelity: 95% for For other states: 0. 93, 0. 92, 0. 91 High fidelity beyond coherence time

Conclusions 1. Diamond-based QIP becomes truly competitive 2. Coherence time can be extended, 25 -fold demonstrated 3. DD can be efficiently combined with gates 4. GARD algorithms demonstrated, 50% longer than T 2 5. 6. Fidelity above 90% First 2 -qubit computation on individual solid state spins