De Morgans Laws 2 9 CS708 1 De

De Morgan’s Laws – 2 - 9 CS-708 1

De Morgan’s Laws – 2 - 9 a CS-708 2

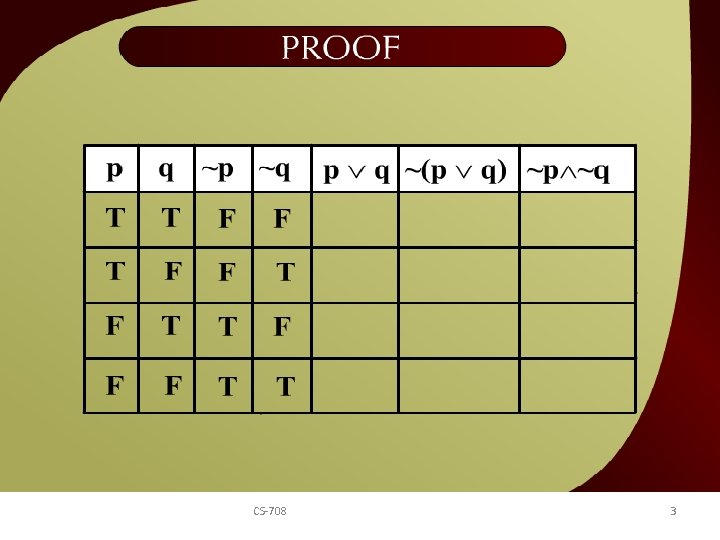
Proof – 2 - 16 CS-708 3

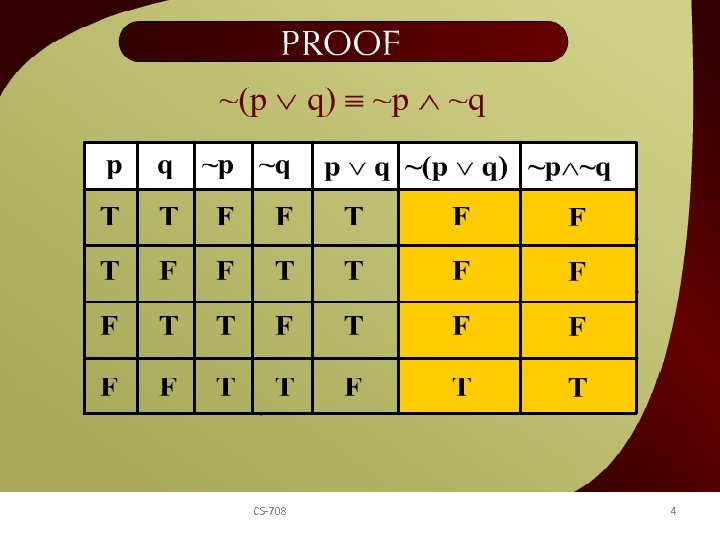
Proof – 2 - 16 d CS-708 4

Application – 2 - 10 CS-708 5

Laws of Logic – 2 - 25 CS-708 6

Laws of Logic – 2 - 25 a CS-708 7

Laws of Logic – 2 - 25 b CS-708 8

Laws of Logic – 2 - 25 c CS-708 9

Laws of Logic – 2 - 25 d CS-708 10

Application - 1 CS-708 11

Example - 2 CS-708 12

Exercise – 5 CS-708 13

Conditional Statements - 6 CS-708 14

Conditional Statements – 6 a CS-708 15

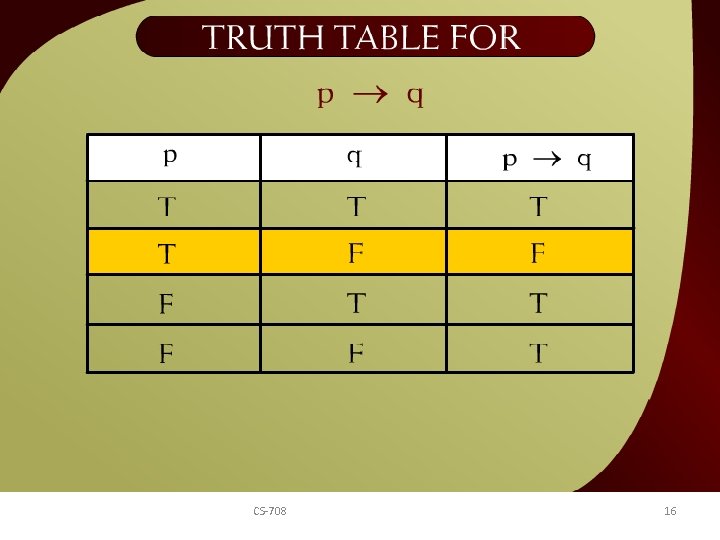
Truth Table for p q - 8 CS-708 16

Conditional Statements or Implications -7 CS-708 17

Conditional Statements OR Implications – 7 a CS-708 18

Example – 9 CS-708 19

Alternative Ways of Expressing Implications – 10 CS-708 20

Alternative Ways of Expressing Implications – 10 a CS-708 21

Exercise - 11 CS-708 22

Exercise – 11 a CS-708 23

Translating English Sentences to Symbols - 12 CS-708 24

Translating English Sentences to Symbols – 12 a CS-708 25

Translating English Sentences to Symbols – 12 b CS-708 26

Translating English Sentences to Symbols – (3 – 12 c) CS-708 27

Translating Symbolic Propositions to English – 13 CS-708 28

Translating Symbolic Propositions to English – 13 a CS-708 29

Translating Symbolic Propositions to English – 13 b CS-708 30

Hierarchy of Operations for Logical Connectives - 14 CS-708 31

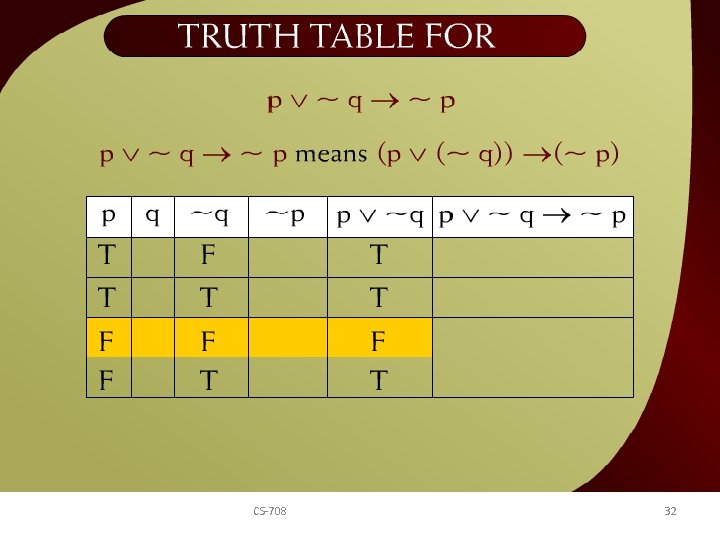
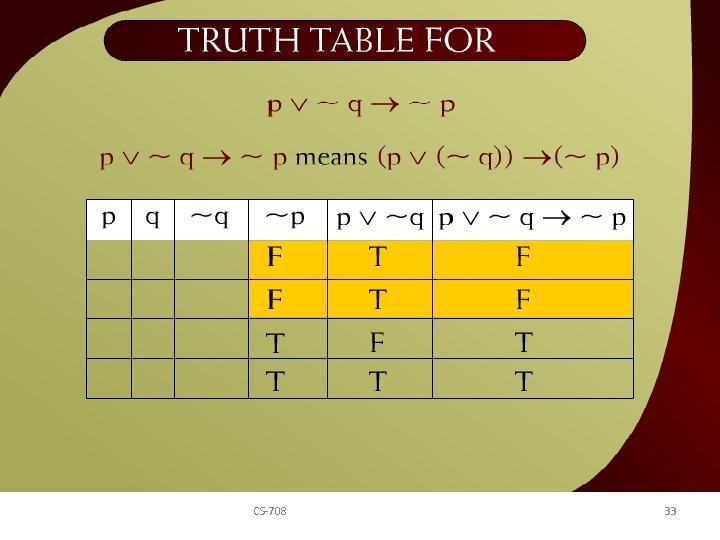
Truth Table for p v ~ q ~ p – 20 a CS-708 32

Truth Table for p v ~ q ~ p – 20 b CS-708 33

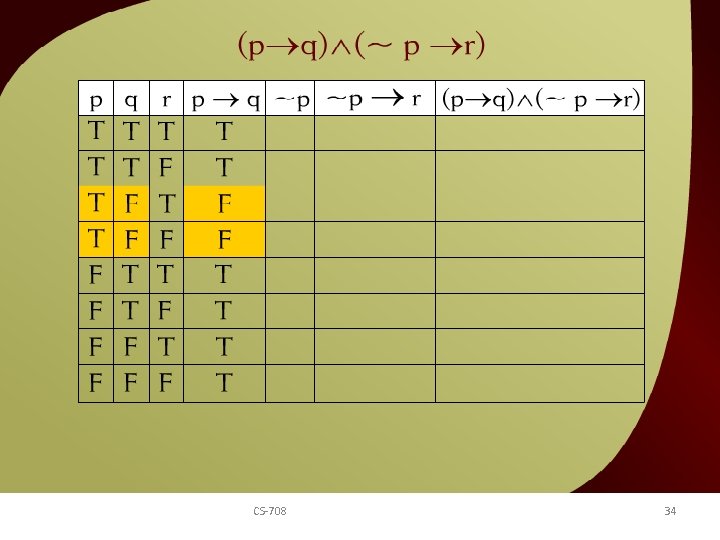
(p q) (~p r) - 21 CS-708 34

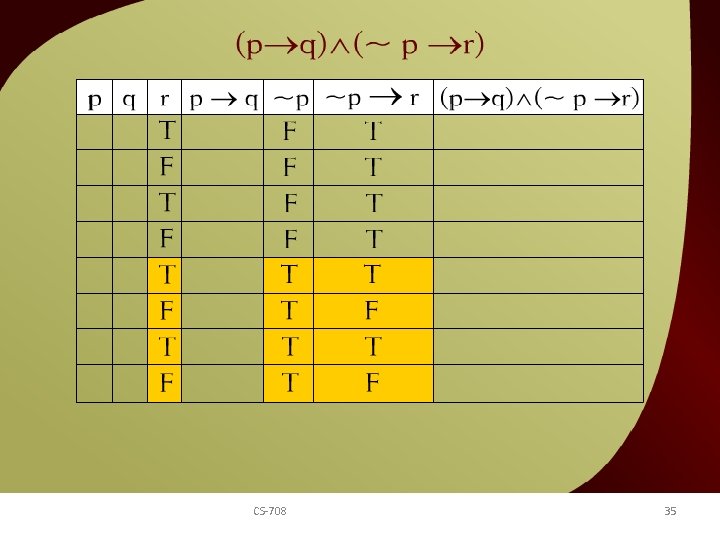
(p q) (~p r) – 21 a CS-708 35

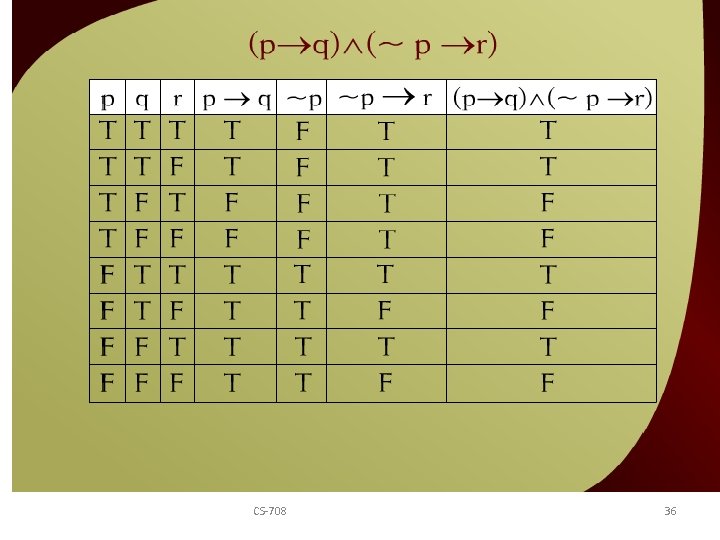
(p q) (~p r) – 21 c CS-708 36

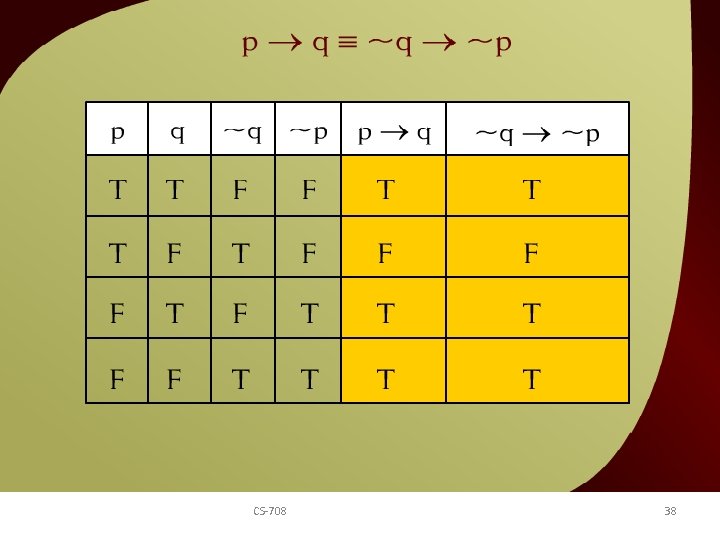
p q ≡ ~q ~p- 22 CS-708 38

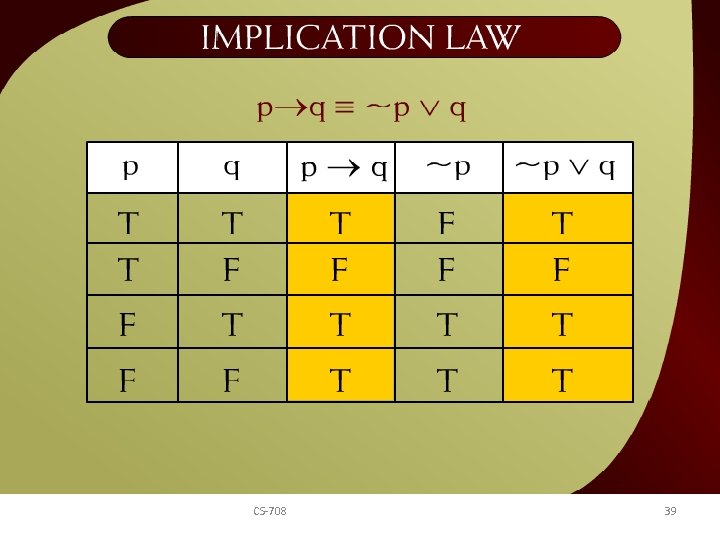
Implication Law – 23 CS-708 39

Negation of a Conditional Statement 15 CS-708 40

Examples – (3 - 16) CS-708 41

Example – 16 a CS-708 42

Inverse of a Conditional Statement - 24 CS-708 43

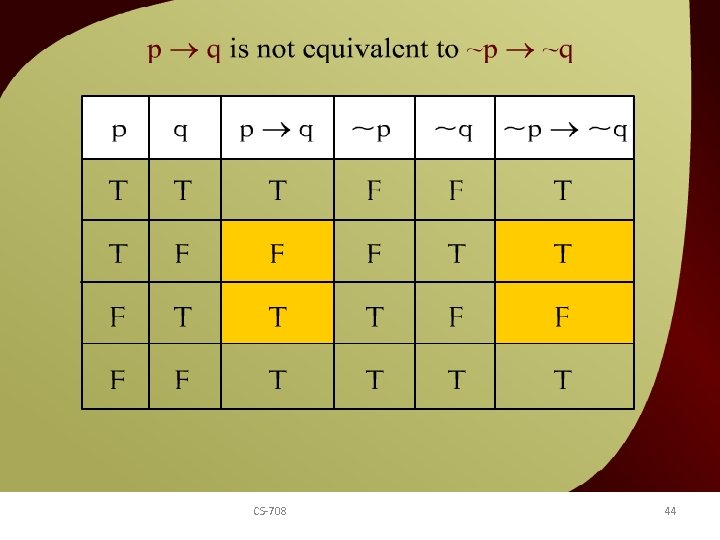
p q is not equivalent to ~p ~q – (3 – 25) CS-708 44

Writing Inverse – 17 CS-708 45

Writing Inverse – 17 a CS-708 46

Converse of a Conditional Statement 26 CS-708 47

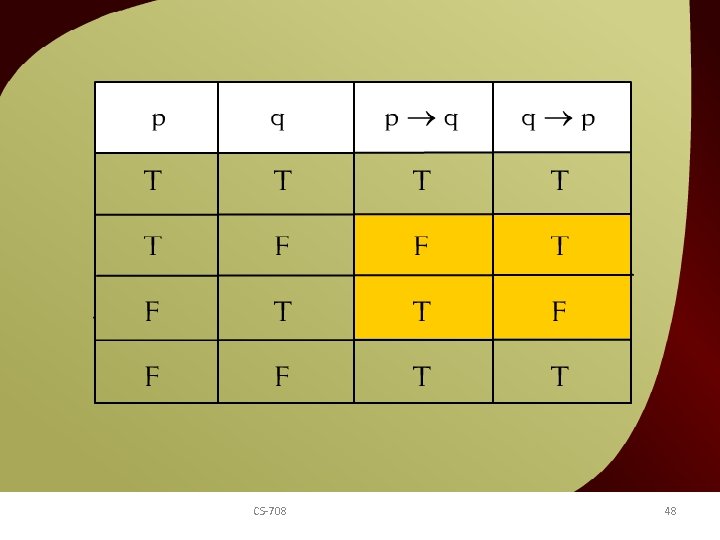
Converse of a conditional Statement – (3 – 27) CS-708 48

Writing Converse – 18 CS-708 49

Writing Converse – 18 a CS-708 50

Contrapositive of a Conditional Statement– 28 CS-708 51

Writing Contrapositivity – 19 CS-708 52

Writing Contrapositivity – 19 a CS-708 53

Biconditional - 2 CS-708 54

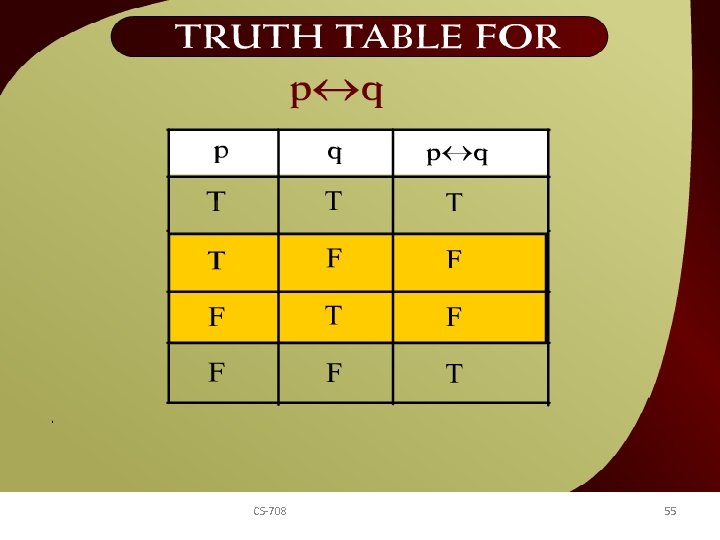
Truth Table for p <--> - 3 CS-708 55

Examples – 4 a CS-708 56

Examples – 4 b CS-708 57

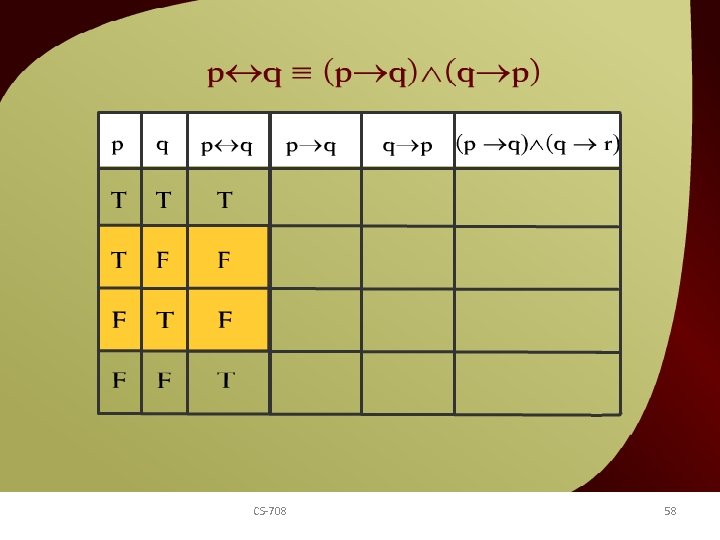
q = (p q) (q p) – 5 a v p CS-708 58

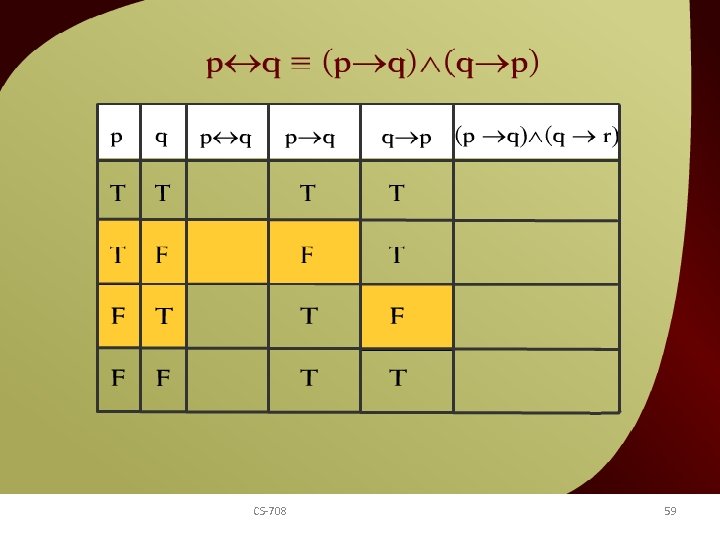
q = (p q) (q p) – 5 b v p CS-708 59

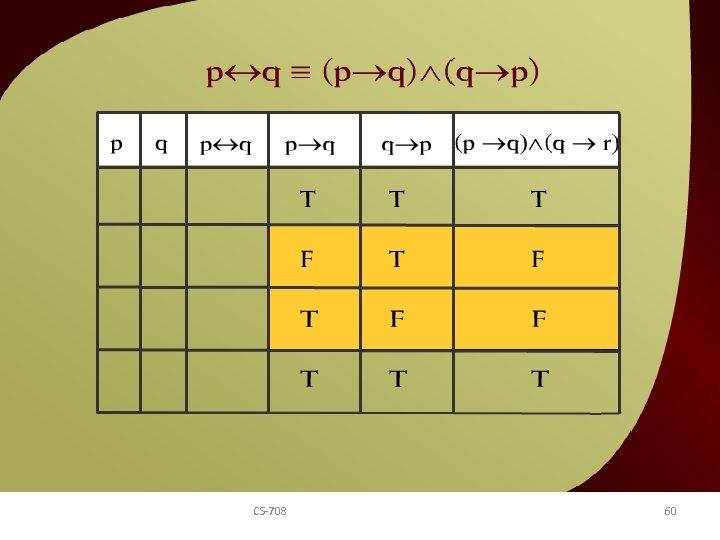
q = (p q) (q p) – 5 c v p – 5 c CS-708 60

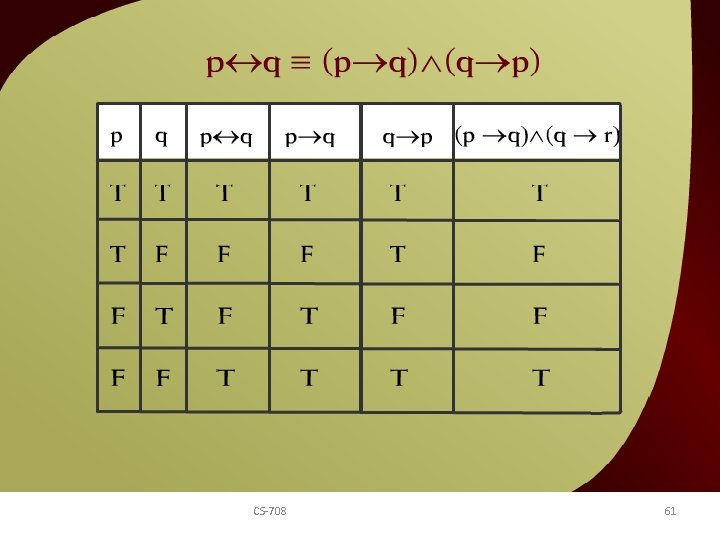
q = (p q) (q p) – 5 v p CS-708 61

Rephrasing Biconditional - 6 CS-708 62

Examples – 9 CS-708 63

Examples – 9 a CS-708 64

Examples – 9 b CS-708 65

Examples – 9 c CS-708 66

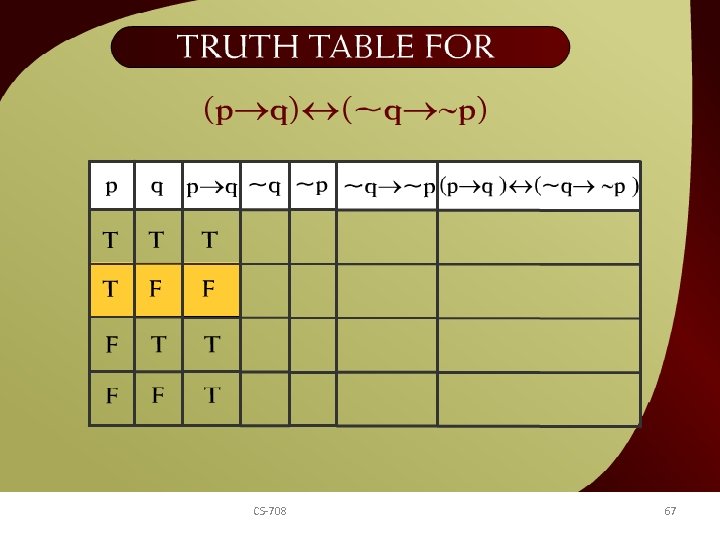
Truth table for (p q) 7 a CS-708 (~q ~p) – 67

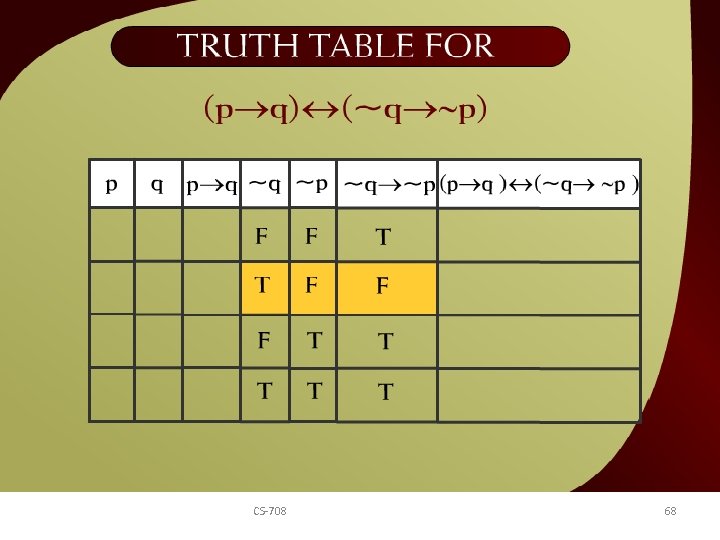
Truth table for (p q) 7 b CS-708 (~q ~p) – 68

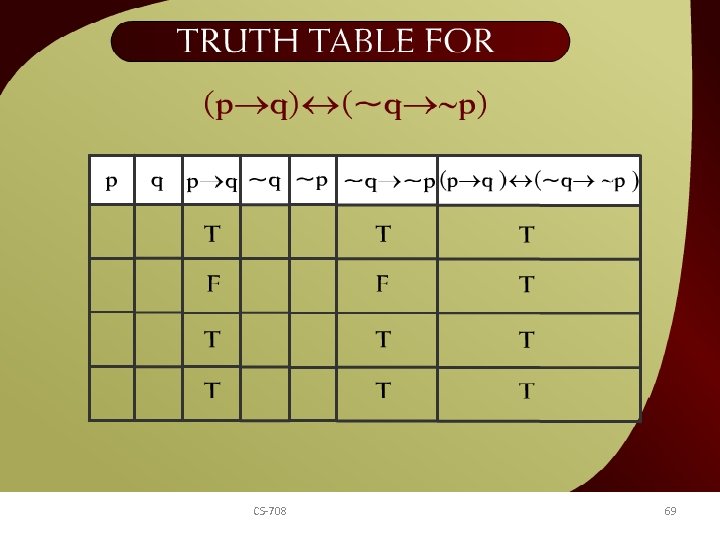
Truth table for (p q) 7 c CS-708 (~q ~p) – 69

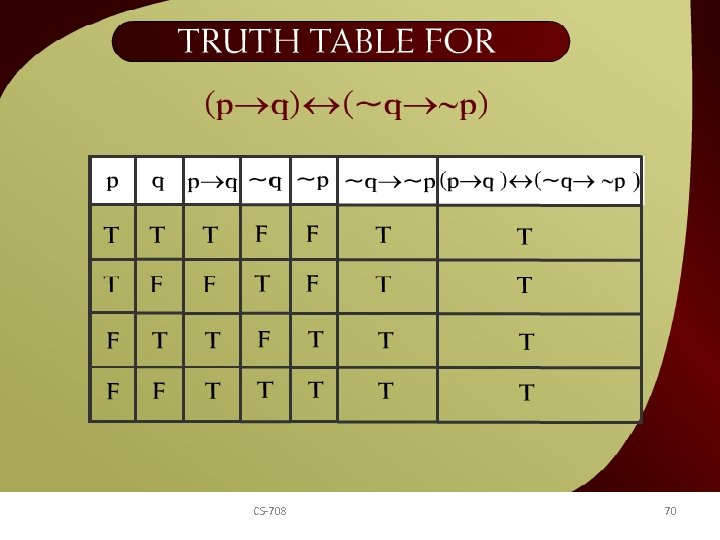
Truth table for (p q) 7 CS-708 (~q ~p) – 70

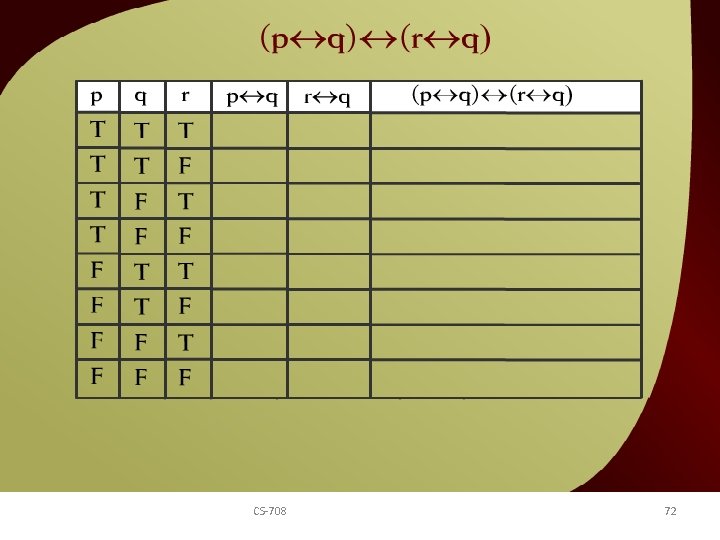
(p q) CS-708 (r q) – 8 72

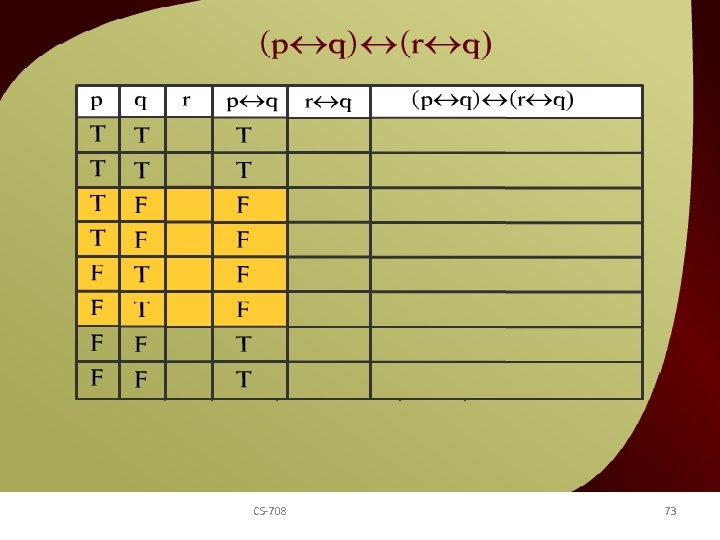
(p q) CS-708 (r q) – 8 b 73

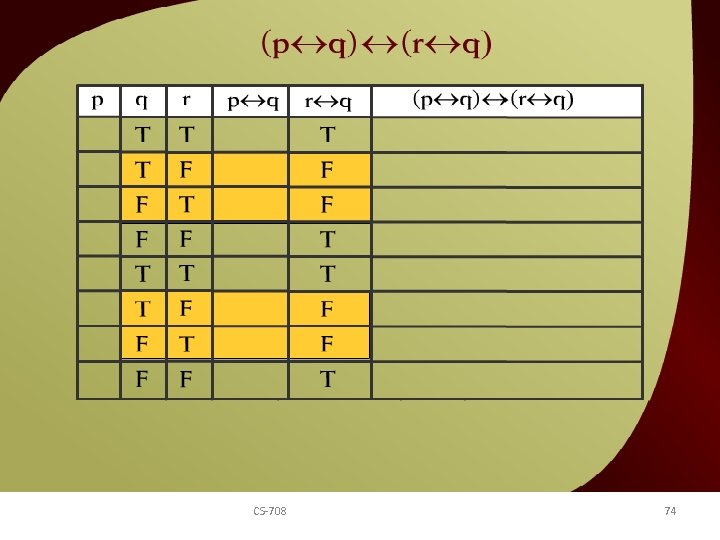
(p q) CS-708 (r q) – 8 c 74

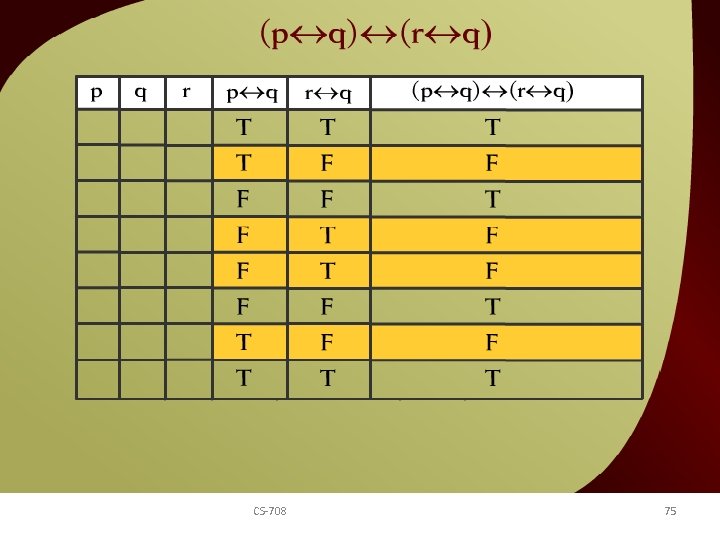
(p q) CS-708 (r q) – 8 d 75

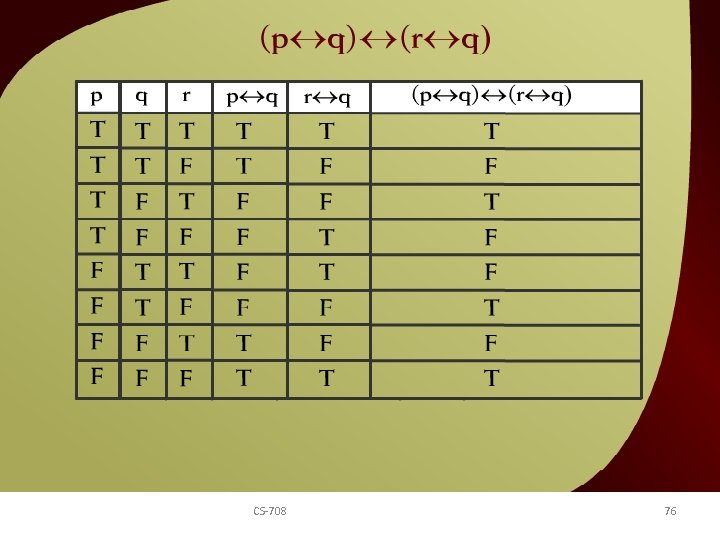
(p q) CS-708 (r q) – 8 76

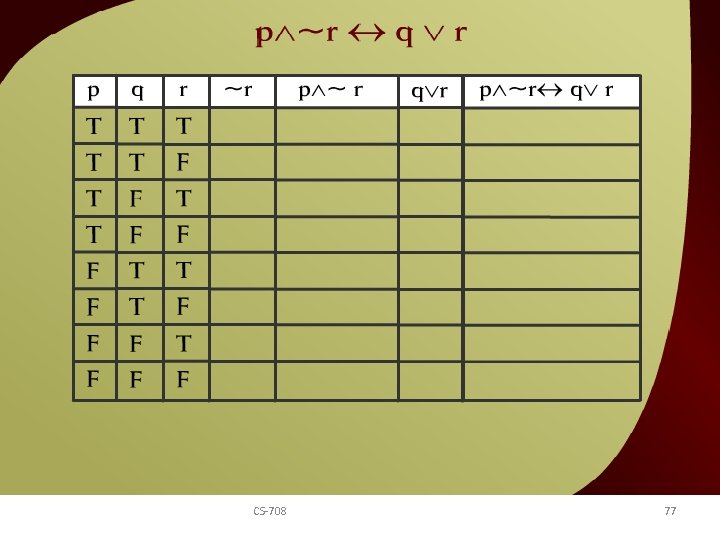
p ~r q v r – 10 CS-708 77 v

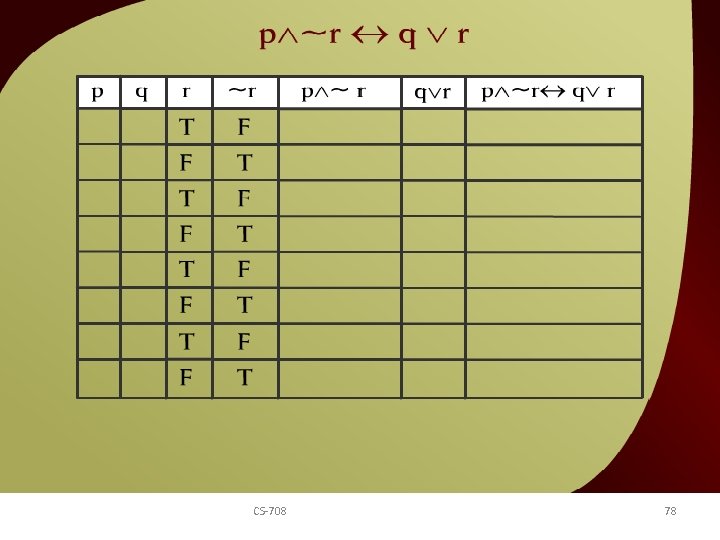
p ~r q v r – 10 b CS-708 78 v

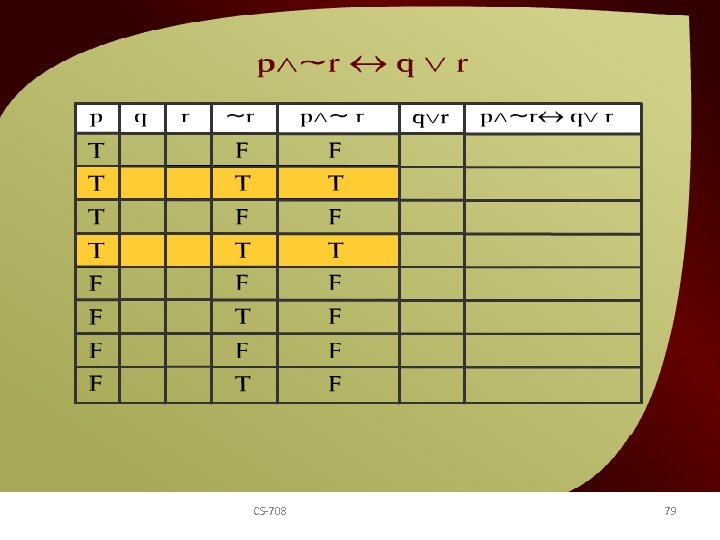
p ~r q v r – 10 c CS-708 79 v

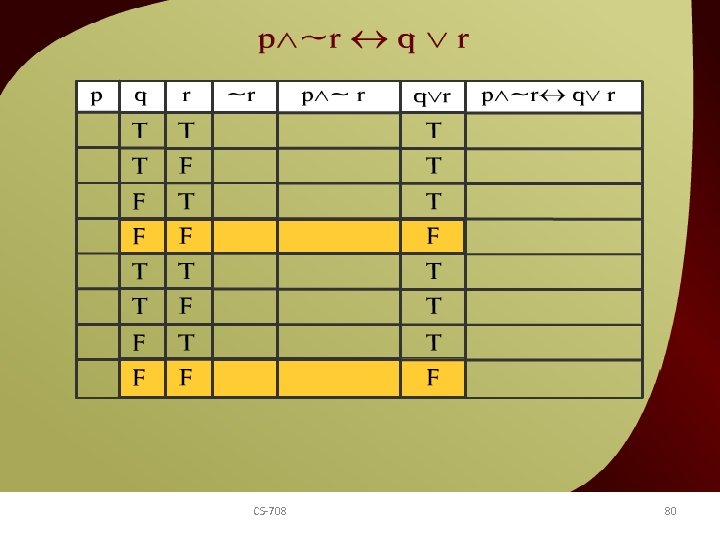
p ~r q v r – 10 d CS-708 80 v

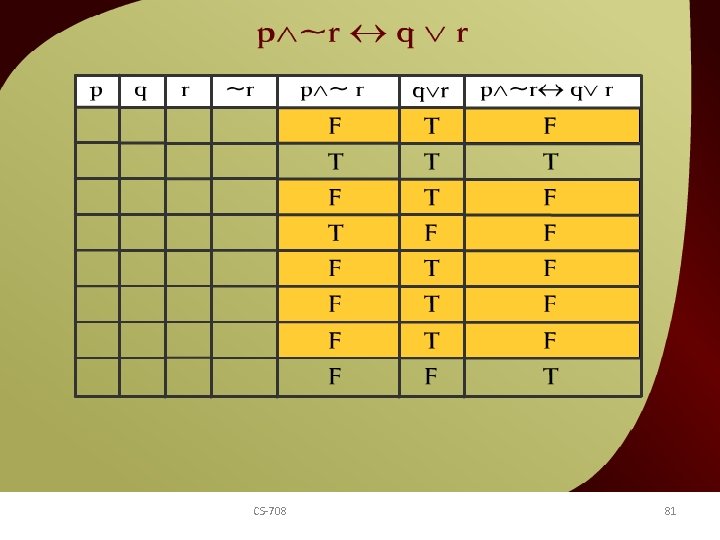
p ~r q v r – 10 e CS-708 81 v

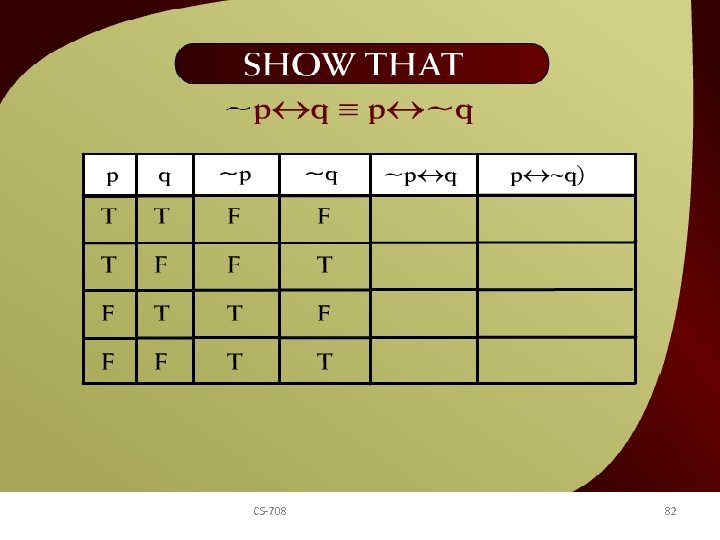
Show that ~p q ≡ p ~q – 11 a CS-708 82

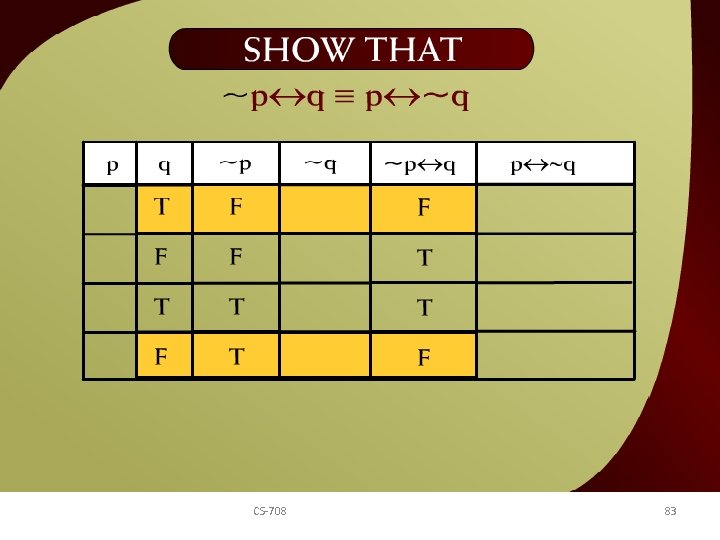
Show that ~p q ≡ p ~q – 11 b CS-708 83

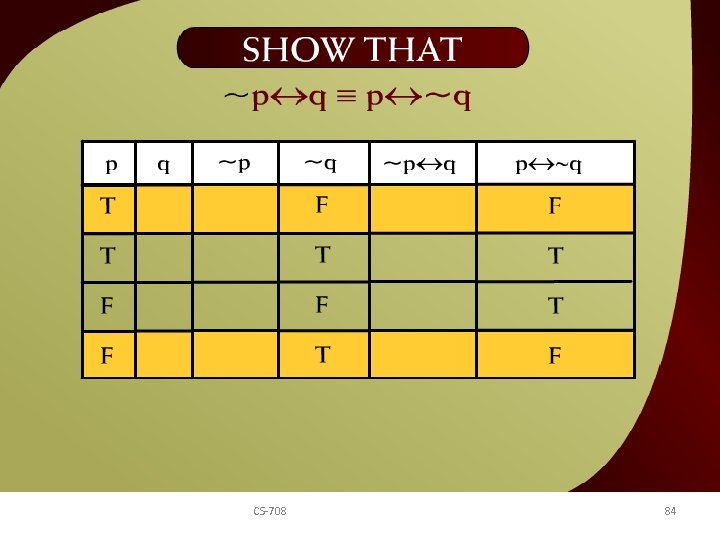
Show that ~p q ≡ p ~q – 11 CS-708 84

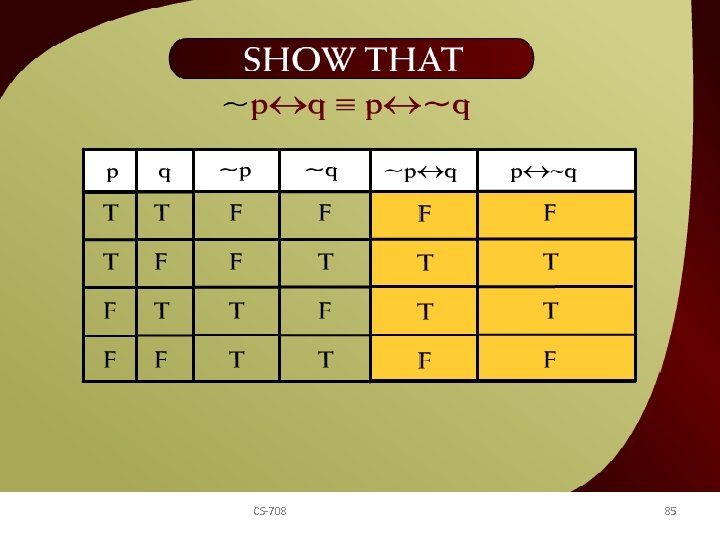
Show that ~p q ≡ p ~q – 11 c CS-708 85

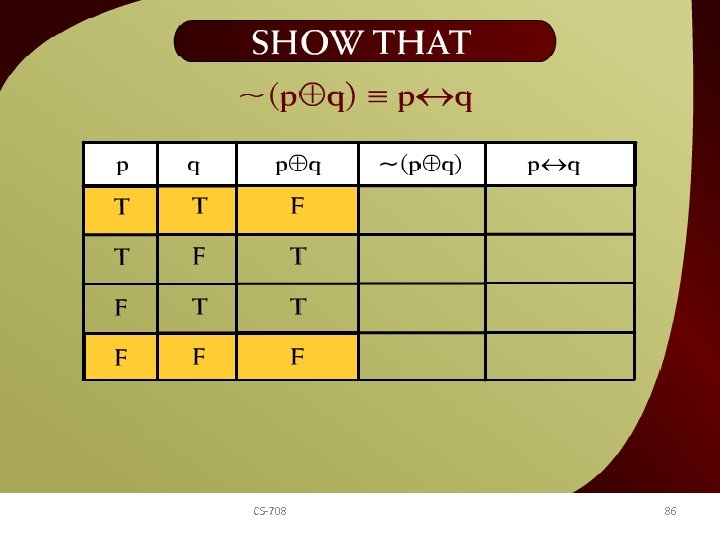
Show that ~(p + q) ≡ p q – 12 b CS-708 86

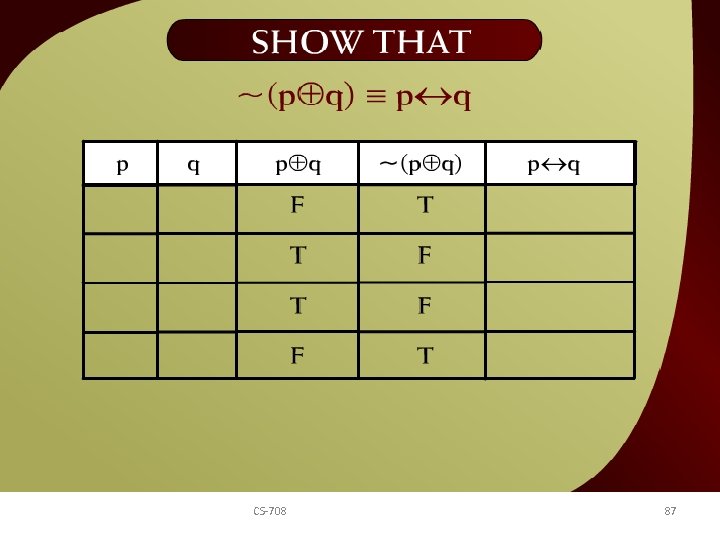
Show That - 1(4 - 2 c) CS-708 87

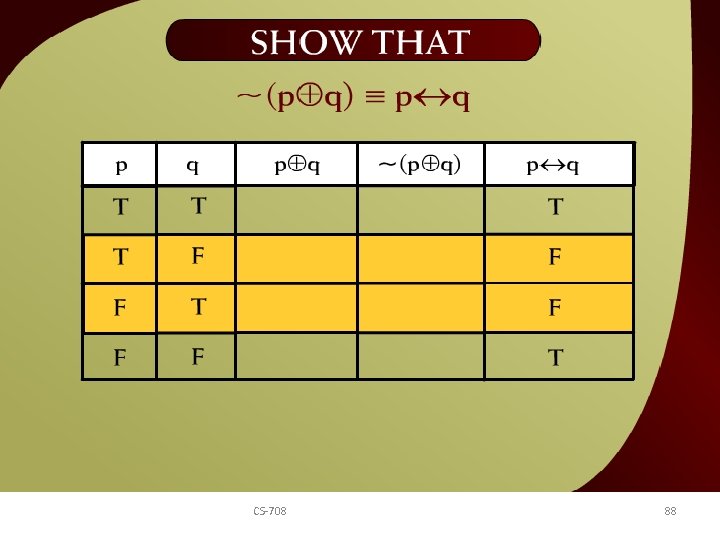
Show that ~(p + q) ≡ p q – 12 d CS-708 88

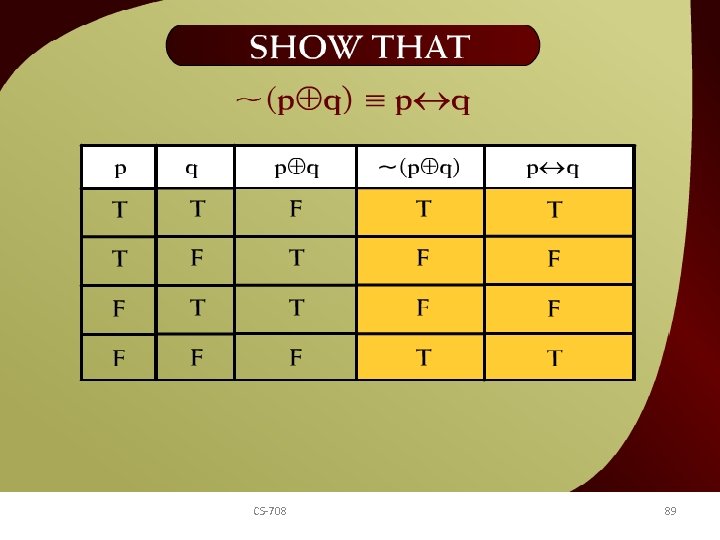
Show that ~(p + q) ≡ p q – 12 CS-708 89

Laws of Logic – 14 CS-708 90

Laws of Logic - 14 a CS-708 91

Application – 15 CS-708 92

Application – 15 b CS-708 93

Exercise - 17 CS-708 94

Exercise – 17 a CS-708 95

Exercise – 17 b CS-708 96