Chapter 3 Force and Newtons laws Section 3

Chapter 3 Force and Newton’s laws

Section 3 -1 Classical mechanics • The approach to the dynamics we consider here is generally called classical mechanics. Galileo Galilei (1564－1642） Issac Newton (1642－1727）

• In this chapter, we will study in detail the bases of classical mechanics: Newton’s three laws. • Classical mechanics was found not to describe well the motions in certain realms. • For ordinary objects, classical mechanics is important and very useful.

Section 3 -2 Newton’s first law § What can cause the motion of a body? Force Take the apple’s freely falling motion as an example § What will be the states of the body if there is no any interactions between it and its environment? (an isolated system) At rest or 1 D uniform motion § Newton’s first law : Every body continues in its state of rest or uniform motion in a straight line, unless it is compelled to change that state by forces impressed on it.

1. Newton’s first law tells us: Consider a body on which no net force acts. 1) If the body is at rest, it will remain at rest； 2) If the body is moving with constant velocity, it will continue to do so, no force is needed to keep it moving.

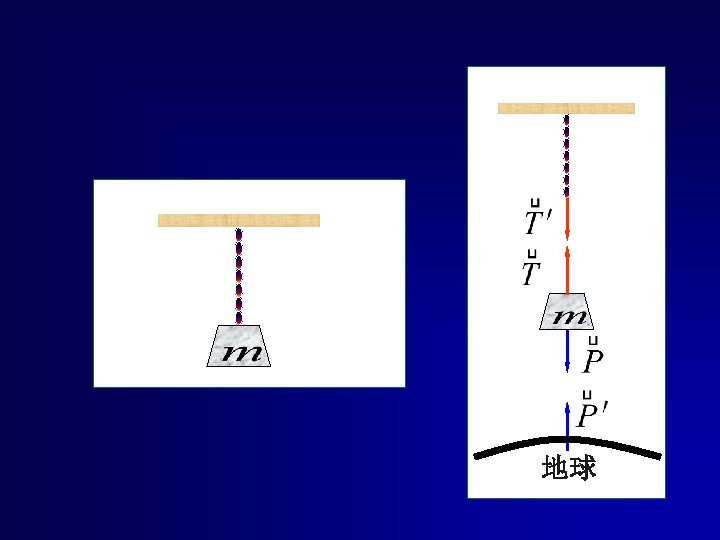
2. The correctness of Newton’s laws is dependent on the reference frames! See an example in 动画库/力学夹/2 -01牛顿定律适用的参照系. exe 1

3. Inertial frames(惯性参考系): • The reference frames to which Newton’s law applies (适用) are called “inertial frames”. • The tendency of a body to remain at rest or in uniform linear motion is called “inertia”. No net force or No acceleration • Can we find inertial frames in the nature?

地心系, 地球赤道加速度 a=3. 4 x 10 -2 m/s 2 日心系, 地球公转轨道加速度 a=6 x 10 -3 m/s 2 银河系, 太阳向心加速度 a=3 x 10 -10 m/s 2 • A frame that keeps rest or uniform linear motion, relative to any inertial frames, is an inertial frame. • Newton’s first law is often called the law of inertia. l See 动画库/力学夹/2 -01德行与惯性. exe

Section 3 -3 Force § Newton’s first law tell us that force causes the change in the motion states (~ ). § For a fixed body, a larger force applied to the body will generate a larger acceleration for the body. § The force is determined through the measure of acceleration the body gets under the force.

Section 3 -4 Mass It is much easy to accelerate a bicycle than a car by pushing it. Clearly same force produces different acceleration when applied to different bodies. What makes the difference? ? ? Mass

In experiments, it is easy to prove that the magnitude of the acceleration is proportional to that of the force applied to a given body. This ratio is called the mass of the body. Thus m=F/a or F=ma Mass : The property of a body that determines its resistance to a change in it’s motion. The mass defined in Newton’s law is an inertial mass.

One method to quantitatively determine the mass of a body, (relative to others’) Suppose we apply a certain force to a body having mass and observe an acceleration of. We then apply the same force to another body of mass , observing an acceleration. Thus or (3 -3)

Section 3 -5 Newton’s second law The mathematical statement of Newton’s second law of motion is (3 -4) 1. Here is the vector sum of all the forces acting on the body. 2. Is the first law not totally contained in second law? No.

3. Equation (3 -4) is a vector equation. We can write it as three one-dimensional equation: (3 -5) Here (or , ) is the algebraic sum of the x (or, y, z) components of all the forces acting on m. 4. If we measure the mass in kg and the acceleration in , Newton’s second law gives the force in N.

Sample problems 1. A worker pushes a loaded sled, whose mass m is 240 kg for a distance d of 2. 3 m over the surface of a frozen lake. The sled moves with negligible friction on the ice. The worker exerts a constant horizontal force of 130 N as she does so. If the sled starts from rest, what is its final velocity?

2. The worker in Sample Problem 1 wants to reverse the direction of the velocity of the sled in 4. 5 s. With what constant force must she push on the sled to do so?

(D) with an increasing (B) speed 3. An object is moving north. From only this information one can conclude: (A) that there is a single force on the object directed north. (B) that there is a net force on the object directed north. (C) that there may be several forces on the object, but the largest must be directed north. (D) nothing about the forces on the object.

Section 3 -6 Newton’s third law 1）Newton’s third law is: To every action there is an equal and opposite reaction. If the body B exerts a force on body A; experiment shows that body A exerts a force on body B. These forces are related by (3 -6) Note: the action and reaction forces always act on different bodies.

2)Dynamical analysis using Newton’s laws In analyzing problems using Newton’s law, there are several steps that we should follow: 1. choose a suitable inertial reference frame. 2. For each object in the problem, draw a “free body diagram”, showing all of the forces acting on that body. 3. For each body, find the vector sum of all the forces. In practice, this usually means separately adding the x, y, z components of the forces. Then use Eqs (3 -5) to find acceleration components

Sample problems 1. A worker W is pushing a packing crate of mass m 1=4. 2 Kg. In front of the crate is a second crate of mass m 2=1. 4 Kg. Both crates slides across the floor without friction. The worker pushes on crate 1 with a force F 1 w=3. 2 N. Find the accelerations of the crates and the force exerted by crate 1 on crate 2. 2. See 动画库/力学夹/2 -02牛顿定律例题 例1