D Menggunakan Turunan untuk Menentukan Karakteristik Suatu fungsi

D. Menggunakan Turunan untuk Menentukan Karakteristik Suatu fungsi dan Pemecahan Masalah Persamaan Garis Singgung pada Kurva Fungsi Naik dan Fungsi Turun Menggambar Grafik Fungsi Aljabar H O M E

Persamaan Garis singgung Pada Kurva Sebelum menentukan persamaan garis singgung pada kurva terlebih dahulu kita harus tahu bahwa turunan pertama merupakan gradien garis singgung di titik (x, y). Persamaan garis singgung pada kurva dapat dibagi 3 kasus yaitu : 1. Persamaan garis singgung dititik (X 1, y 1) pada kurva Rumus persamaan garis yang menyinggung kurva y = f (x) di titik (X 1, y 1) adalah : contoh Dengan gradien nex Hsc

Contoh : Tentukan persamaan garis singgung yang menyinggung kurva y = x 2 + x – 5 di titik (2, 1). Solusi : Langkah pertama adalah kita menentukan terlebih dahulu gradiennya Ingat m = f ‘ (x 1), sehingga : F ‘(x) = 2 x + 1, f ‘(x 1)=2 x 1 + 1 F ‘(2) = 2. 2 + 1 = 5, m = f ‘(2) = 5 Jadi m = 5 Persamaan garis yang melalui titik (2, 1) dengan m = 5 adalah Y – y 1 = m (x – x 1) Y – 1 = 5 (x – 2) Y = 5 x – 9 Jadi persamaan garis singgungnya adalah y = 5 x - 9 HS

2. Persamaan Garis singgung Bergradien m langkah untuk menentukan persamaan garis singgung pada kurva jika diketahui gradien dan persamaan kurvanya saja adalah dengan menentukan titik singgung pada kurvanya, dengan mengingat bahwa : Kemudian kita subtitusikan nilai m untuk menperoleh X 1 dan setelah itu kita subtitusikan ke persamaan awal untuk menentukan y 1, maka didapatlah titik singgungnya (x 1, y 1). contoh Nex Back

contoh : tentukan persamaan garis yang bergradien 2 dan menyinggung kurva y = x 2 + 4 x + 3. Solusi : Mencari titik singgung y = x 2 + 4 x + 3 F ‘(x 1) = 2 x 1 + 4, karena m = f ‘(x 1) maka : m = 2 x 1 + 4, dimana m = 2 sehingga 2 = 2 x 1 + 4, x 1 = -1 Y 1 = x 21 + 4 x 1 + 3 Y 1 = (-1)2 + 4 (-1) +3 Y 1 = 0, didapatlah titik singgungnya adalah (x 1, y 1) = (1, 0) Persamaan garis yng melalui titik (-1, 0) dengan m = 2 adalah Y – y 1 = m (x – x 1) Y – 0 = 2 (x –(-1)) Y = 2 x + 2 Jadi persamaan garisnya adalah y = 2 x + 2 HS

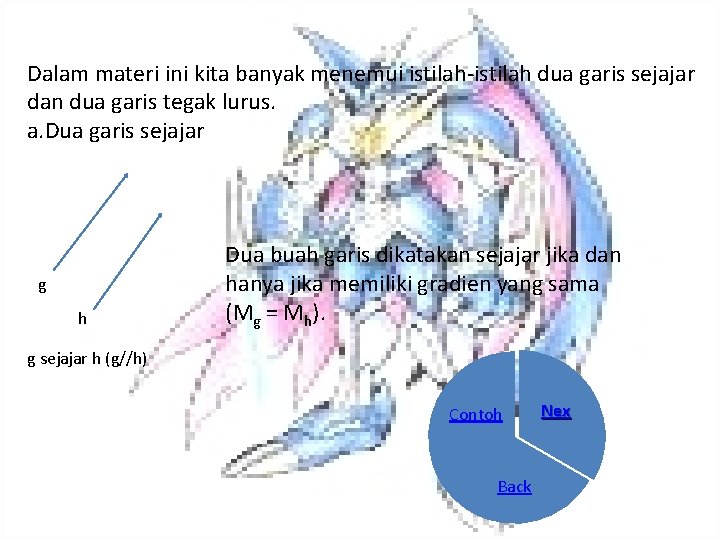
Dalam materi ini kita banyak menemui istilah-istilah dua garis sejajar dan dua garis tegak lurus. a. Dua garis sejajar g h Dua buah garis dikatakan sejajar jika dan hanya jika memiliki gradien yang sama (Mg = Mh). g sejajar h (g//h) Contoh Back Nex

Contoh : Tentukan persamaan garis yang sejajar dengan garis y = 3 x + 5 dan menyinggung kurva y = x 2 – x + 4. Solusi : Karena garis singgung sejajar dengan garis y = 3 x + 5 maka m 1 = m 2. Gradien garis y = 3 x + 5 adalah m 1 = 3 karena sejajar maka m 2 = 3. Menentukan titik singgungnya m = f ‘(x 1) , f ‘(x) = 2 x -1 f ‘(x 1) = 2 x 1 – 1 , 3 = 2 x 1 -1 , x 1 = 2 subtitusikan x 1 = 2 ke fungsi y = x 2 – x + 4 untuk mencari nilai y 1 = (2)2 -2 + 4 = 6, jadi titik singgungnya adalah (2, 6) persamaan garisnya adalah y-y 1 =m(x-x 1) y = 3 x jadi persamaan garisnya adalah y =3 x HS

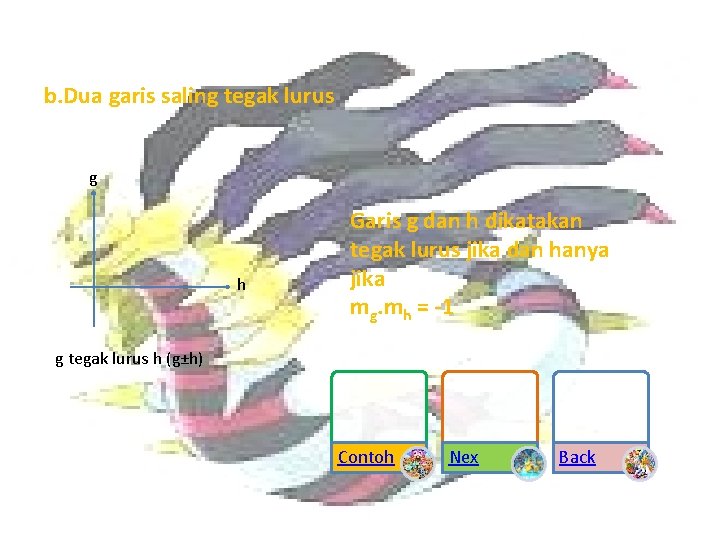
b. Dua garis saling tegak lurus g h Garis g dan h dikatakan tegak lurus jika dan hanya jika mg. mh = -1 g tegak lurus h (g±h) Contoh Nex Back

Contoh : Tentukan persamaan garis yang tgak lurus dengan garis y = 3 x + 5 dan menyinggung kurva y = x 2 – x + 4. Solusi : Karena garis singgung tegak lurus dengan garis y = 3 x + 5 maka m 1 m 2 = -1 Gradien garis y = 3 x + 5 adalah m 1 = 3 karena tegak lurus maka m 2 = -1/3. Menentukan titik singgungnya m = f ‘(x 1) , f ‘(x) = 2 x -1 f ‘(x 1) = 2 x 1 – 1 , -1/3 = 2 x 1 -1 , x 1 = 1/3 subtitusikan x 1 = 1/3 ke fungsi y = x 2 – x + 4 untuk mencari nilai y 1 = (1/3)2 -1/3 + 4 = 34/9, jadi titik singgungnya adalah (1/3, 34/9) persamaan garisnya adalah y-y 1 =m(x-x 1) 9 y = 35 – 3 x jadi persamaan garisnya adalah 9 y = 35 - 3 x HS

3. Garis Singgung melalui titik (x 1, y 1) diluar kurva untuk menentukan persamaan garis singgung, jika diketahui sebuah titik (x 1, y 1) terletak di luar kurva adalah dengan mencari gradienya, akan tetapi sebelum itu kita harus menentukan a dengan memisalkan titik singgungnya adalah [a, f(a)]. Rumus : Contoh Back Hsc

Tentukan persamaan garis yang melalui titik (0, -2) dan menyinggung kurva y=x 3. Solusi : Titik ( 0, -2 ) berada diluar kurva, karena -2 ≠ 0 3. Misalkan : y = f(x) = x 3, maka f ‘(x) = 3 x 2. Mencari nilai a, Persamaan garis singgunya : y-y 1 =m (x – x 1) Y-(-2) = 3(x-0) Y = 3 x – 2 a 3 + 2 = 3 a 3 a = 1, m = f ‘(a) =f ‘(1) =3 HS

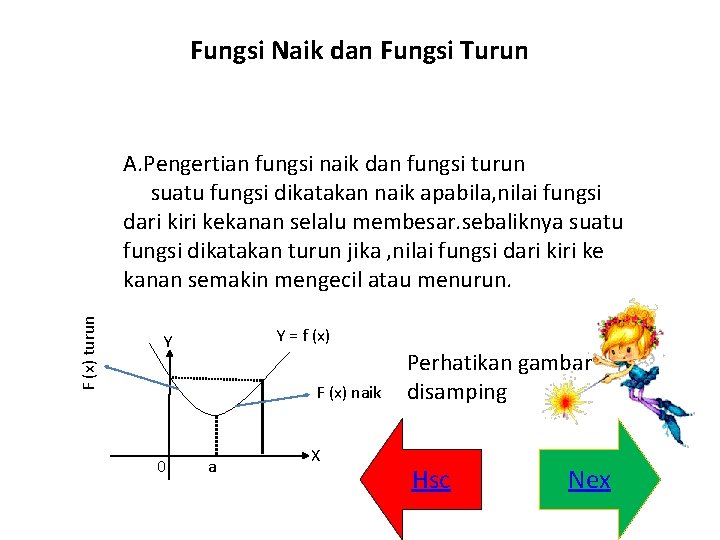
Fungsi Naik dan Fungsi Turun F (x) turun A. Pengertian fungsi naik dan fungsi turun suatu fungsi dikatakan naik apabila, nilai fungsi dari kiri kekanan selalu membesar. sebaliknya suatu fungsi dikatakan turun jika , nilai fungsi dari kiri ke kanan semakin mengecil atau menurun. Y = f (x) Y F (x) naik 0 a X Perhatikan gambar disamping Hsc Nex

Berdasarkan gambar disamping diperoleh : 1. Fungsi f (x) merupakan fungsi naik dalam interval x > a, karena dalam interval tersebut jika nilai x semakin besar maka nilai fungsi f(x) pun semakin besar. 2. Fungsi f (x) merupakan fungsi turun dalam interval x < a, karena dalam interval tersebut jika nilai x semakin besar maka nilai fungsi f (x) semakin kecil Nex Back

B. Menentukan interval suatu fungsi naik atau fungsi turun untuk menentukan interval fungsi f(x) naik adalah dengan menyelesaikan pertidaksamaan f ‘(x) > 0. demikian juga untuk menentukan interval fungsi f(x) turun adalah dengan menyelesaikan pertidak samaan f ‘(x) < 0. Contoh Nex Back

Contoh : tentukan interval-interval dari fungsi f(x) = x 2 – 4 x agar fungsi : a. naik b. turun solusi : a. naik f(x) = x 2 -4 x, f ‘(x) = 2 x – 4 syarat fungsi naik f ‘(x) > 0 sehingga : f ‘(x) > 0 2 x – 4 > 0 X>2 2 b. Turun F ‘(x) = 2 x -4 Syarat fungsi turun f ‘(x) < 0 sehingga F ‘(x) < 0 2 x – 4 < 0 X<2 2 HSC

C. Nilai Stasioner Y (a, f(a))→titik stasioner F (a) F(a)→nilai stasioner 0 a X Perhatikan gambar diatas : Fungsi y = f(x) dengan x = a dan f ‘(a) = 0, maka f (a) merupakan nilai stasioner dari fungsi f(x) di x = a dan (a, f(a)) merupakan titik stasionernya. nilai stasioner disebut juga nilai kritis dan titik stasioner disebut juga titik kritis N e x

Jenis-jenis nilai stasioner 1. Maksimum Syarat f ‘ (x) = 0 f “(x) < 0 2. Minimum Syarat : f ‘ (x) = 0 f “ (x) > 0 3. Titik belok Syarat : f ‘(x) = 0 f “(x) = 0 Contoh Nex Back

contoh : diketahui fungsi f(x) = 2 x 3 + 3 x 2 -12 x + 4 tentukan : a. nilai-nilai stasionernya b. jenis-jenis stasionernya solusi : a. fungsi f(x) = 2 x 3 + 3 x 2 -12 x + 4 f ‘(x) = 6 x 2 + 6 x – 12 syarat stasioner f ‘(x) = 0, maka 6 x 2 + 6 x – 12 = 0 6 (x + 2) (x-1) = 0 X 1 = -2 dan x 2 = 1 Untuk x = -2 maka f (-2) =2(-2)3 + 3(-2)2 -12(-2) + 4 = 24 untuk x = 1 maka, f (1) = 2 (1)3 + 3(1)2 -12(1) +4 = -3 jadi nilai stasionernya adalah 24 dan -3 NEX

b. f “(x) = 12 x + 6 untuk x = -2 maka 12(-2) + 6 < 0 Karena f “(x) < 0 maka maksimum Jadi f(-2) = 24 merupakan nilai balik maksimum Untuk x = 1 maka, 12(1) + 6 > 0, karena f”(1) > 0 maka minimum Jadi f(1) = -3 merupakan nilai balik minimum BACK HS

Menggambar Grafik Fungsi Aljabar Langkah –langkah dalam menggambar grafik suatu fungsi aljabar adalah sebagai berikut : ØMenentukan titik potong dengan sumbu-sumbu koordinat (sumbu x dan sumbu y ) ØMenentukan titik-titik stasioner dan jenisnya (titik balik maksimum, minimum, dan titik beloknya ) ØMenentukan nilai y untuk x besar positif dan untuk x besar negatif. B Catatan : F(x) = ax 2 + bx + c A a > 0 dan D < 0 maka f ‘ (x) definit positif C atau f ‘(x) > 0 K Home

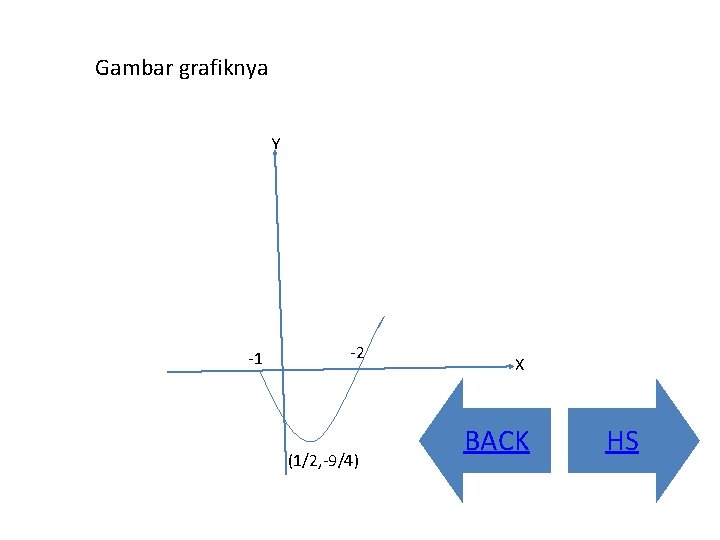
contoh : gambarlah kurva dari fungsi y = x 2 – x – 2 solusi : menentukan titik potong dengan sumbu x maka y = 0 x 2 – x – 2 = 0 (x – 2) (x + 1) = 0 X = 2 atau x =-1 Koordinat titiknya (2, 0) dan (-1, 0) Menentukan titik potong dengan sumbu y maka x = 0 Y = 02 – 0 – 2 Y = -2, koordinat titiknya adalah (0, -2) Menentukan nilai ekstrim X = -b/2 a dan y = -D/ 4 a X =1/2, y =-9/4 Koordinat titiknya adalah (1/2, -9/4) NEX

Gambar grafiknya Y -1 -2 (1/2, -9/4) X BACK HS