CS 140 Nonnumerical Examples with Cilk Divide and

CS 140 : Non-numerical Examples with Cilk++ • Divide and conquer paradigm for Cilk++ • Quicksort • Mergesort Thanks to Charles E. Leiserson fo 1

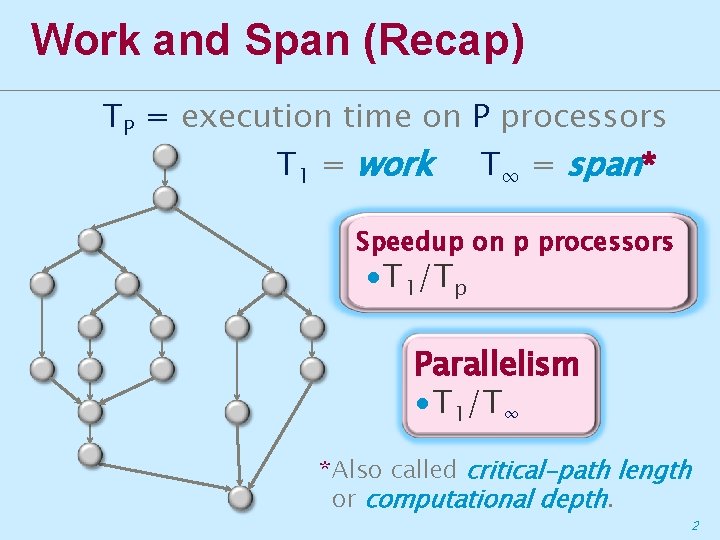
Work and Span (Recap) TP = execution time on P processors T 1 = work T∞ = span* Speedup on p processors ∙T 1/Tp Parallelism ∙T 1/T∞ *Also called critical-path length or computational depth. 2

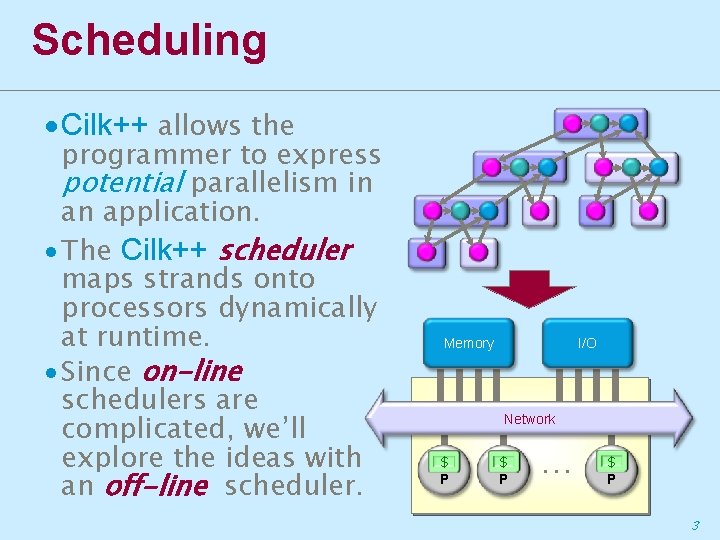
Scheduling ∙Cilk++ allows the programmer to express potential parallelism in an application. ∙ The Cilk++ scheduler maps strands onto processors dynamically at runtime. ∙ Since on-line schedulers are complicated, we’ll explore the ideas with an off-line scheduler. Memory I/O Network $ P P $ P … $ P 3

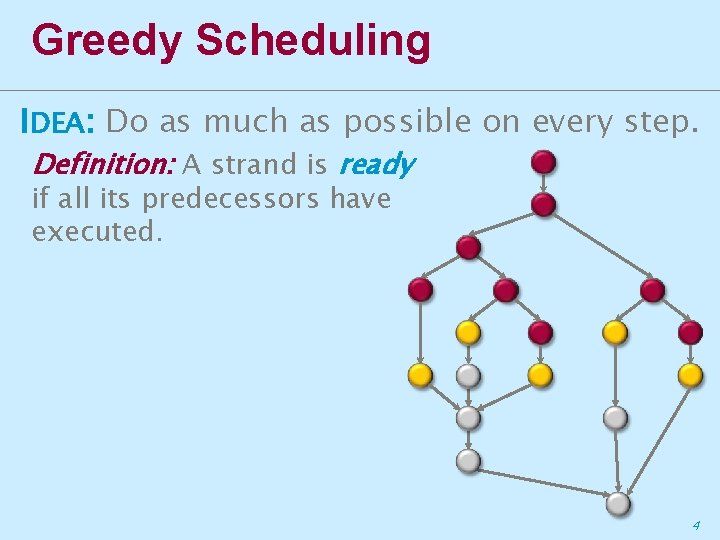
Greedy Scheduling IDEA: Do as much as possible on every step. Definition: A strand is ready if all its predecessors have executed. 4

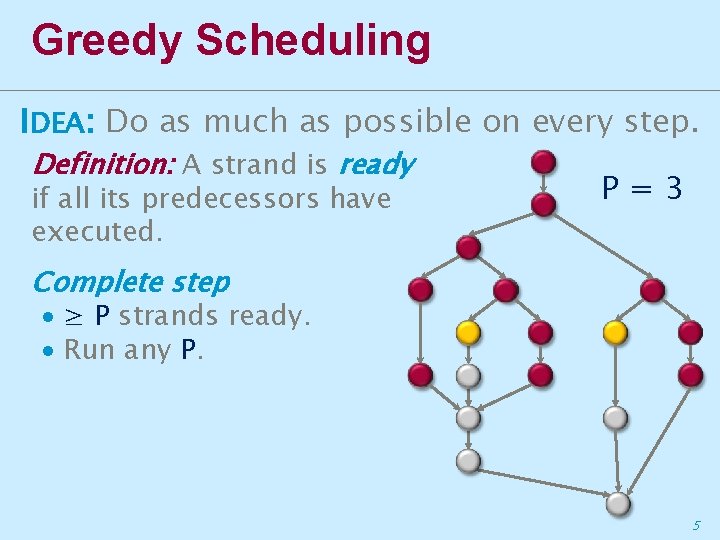
Greedy Scheduling IDEA: Do as much as possible on every step. Definition: A strand is ready if all its predecessors have executed. P=3 Complete step ∙ ≥ P strands ready. ∙ Run any P. 5

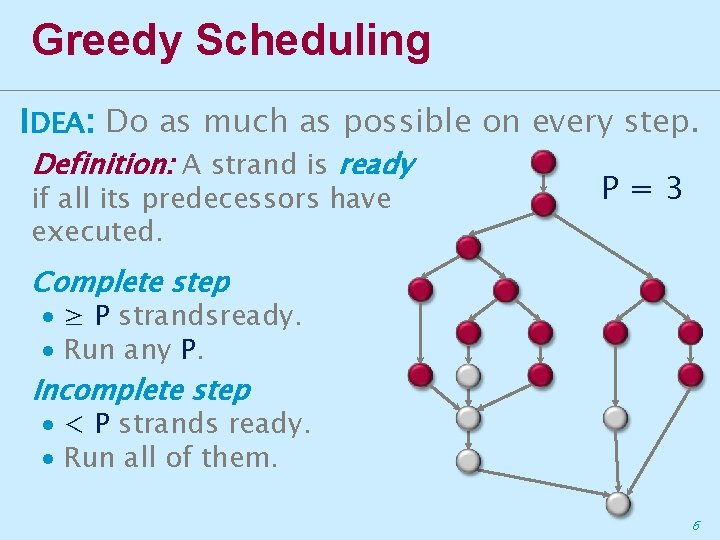
Greedy Scheduling IDEA: Do as much as possible on every step. Definition: A strand is ready if all its predecessors have executed. P=3 Complete step ∙ ≥ P strandsready. ∙ Run any P. Incomplete step ∙ < P strands ready. ∙ Run all of them. 6

Analysis of Greedy Theorem [G 68, B 75, BL 93]. Any greedy scheduler achieves TP T 1/P + T∞. Proof. ∙ # complete steps T 1/P, P=3 since each complete step performs P work. ∙ # incomplete steps T∞, since each incomplete step reduces the span of the unexecuted dag by 1. ■ 7

Optimality of Greedy Corollary. Any greedy scheduler achieves within a factor of 2 of optimal. Proof. Let TP* be the execution time produced by the optimal scheduler. Since TP* ≥ max{T 1/P, T∞} by the Work and Span Laws, we have TP ≤ T 1/P + T∞ ≤ 2⋅max{T 1/P, T∞} ≤ 2 TP*. ■ 8

Linear Speedup Corollary. Any greedy scheduler achieves near-perfect linear speedup whenever P ≪ T 1/T∞. Proof. Since P ≪ T 1/T∞ is equivalent to T∞ ≪ T 1/P, the Greedy Scheduling Theorem gives us TP ≤ T 1/P + T∞ ≈ T 1/P. Thus, the speedup is T 1/TP ≈ P. ■ Definition. The quantity T 1/PT∞ is called the parallel slackness. 9

Sorting ∙ Sorting is possibly the most frequently executed operation in computing! ∙ Quicksort is the fastest sorting algorithm in practice with an average running time of O(N log N), (but O(N 2) worst case performance) ∙ Mergesort has worst case performance of O(N log N) for sorting N elements ∙ Both based on the recursive divide-andconquer paradigm 10

Parallelizing Quicksort ∙ Serial Quicksorts an array S as follows: § If the number of elements in S is 0 or 1, then return. § Pick any element v in S. Call this pivot. § Partition the set S-{v} into two disjoint groups: S 1 = {x S-{v} | x v} ♦ S 2 = {x S-{v} | x v} ♦ § Return quicksort(S 1) followed by v followed by quicksort(S 2) Not necessarily so ! 11

Parallel Quicksort (Basic) • The second recursive call to qsort does not depend on the results of the first recursive call • We have an opportunity to speed up the call by making both calls in parallel. 12

Performance ∙. /qsort 500000 -cilk_set_worker_count 1 >> 0. 122 seconds ∙. /qsort 500000 -cilk_set_worker_count 4 >> 0. 034 seconds ∙ Speedup = T 1/T 4 = 0. 122/0. 034 = 3. 58 ∙. /qsort 50000000 -cilk_set_worker_count 1 >> 14. 54 seconds ∙. /qsort 50000000 -cilk_set_worker_count 4 >> 3. 84 seconds ∙ Speedup = T 1/T 4 = 14. 54/3. 84 = 3. 78 13

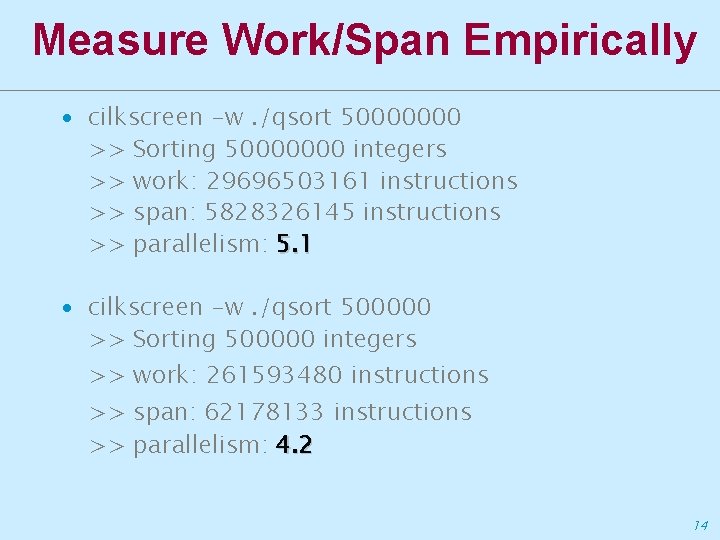
Measure Work/Span Empirically ∙ cilkscreen -w. /qsort 50000000 >> Sorting 50000000 integers >> work: 29696503161 instructions >> span: 5828326145 instructions >> parallelism: 5. 1 ∙ cilkscreen -w. /qsort 500000 >> Sorting 500000 integers >> work: 261593480 instructions >> span: 62178133 instructions >> parallelism: 4. 2 14

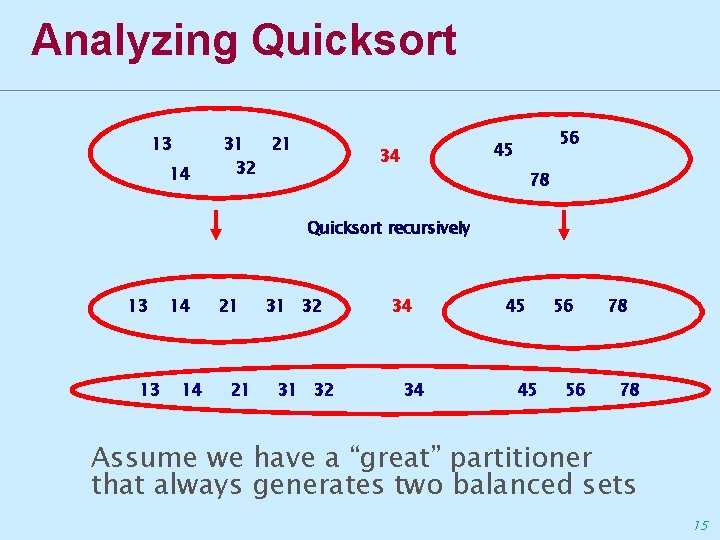
Analyzing Quicksort 13 14 31 21 32 56 45 34 78 Quicksort recursively 13 13 14 14 21 21 31 32 34 34 45 45 56 56 78 78 Assume we have a “great” partitioner that always generates two balanced sets 15

Analyzing Quicksort ∙ Work: T 1(n) = 2 T 1(n/2) + Θ(n) 2 T 1(n/2) = 4 T 1(n/4) + 2 Θ(n/2) …. …. + n/2 T 1(2) = n T 1(1) + n/2 Θ(2) T 1(n) = Θ(n lg n) ∙ Span recurrence: T∞(n) = T∞(n/2) + Θ(n) Solves to T∞(n) = Θ(n) 16

Analyzing Quicksort Parallelism: T 1(n) T∞(n) = Θ(lg n) Not much ! ∙ Indeed, partitioning (i. e. , constructing the array S 1 = {x S-{v} | x v}) can be accomplished in parallel in time Θ(lg n) ∙ Which gives a span T∞(n) = Θ(lg 2 n ) ∙ And parallelism Θ(n/lg n) Way better ! ∙ Basic parallel qsort can be found under $cilkpath/examples/qsort ∙ Parallel partitioning might be a final project 17

The Master Method (Optional) The Master Method for solving recurrences applies to recurrences of the form T(n) = a T(n/b) + f(n) *, where a ≥ 1, b > 1, and f is asymptotically positive. IDEA: Compare nlogba with f(n). * The unstated base case is T(n) = (1) for sufficiently small n. 18

Master Method — CASE 1 T(n) = a T(n/b) + f(n) nlogba ≫ f(n) Specifically, f(n) = O(nlogba – ε) for some constant ε > 0. Solution: T(n) = Θ(nlogba). 19

Master Method — CASE 2 T(n) = a T(n/b) + f(n) nlogba ≈ f(n) Specifically, f(n) = Θ(nlogbalgkn) for some constant k ≥ 0. Solution: T(n) = Θ(nlogbalgk+1 n)). Ex(qsort): a =2, b=2, k=0 T 1(n)=Θ(n lg n) 20

Master Method — CASE 3 T(n) = a T(n/b) + f(n) nlogba ≪ f(n) Specifically, f(n) = Ω(nlogba + ε) for some constant ε > 0, and f(n) satisfies the regularity condition that a f(n/b) ≤ c f(n) for some Example: Span constant c < 1. Solution: T(n) = Θ(f(n)). of qsort 21

Master Method Summary T(n) = a T(n/b) + f(n) CASE 1: f (n) = O(nlogba – ε), constant ε > 0 T(n) = Θ(nlogba). CASE 2: f (n) = Θ(nlogba lgkn), constant k 0 T(n) = Θ(nlogba lgk+1 n). CASE 3: f (n) = Ω(nlogba + ε), constant ε > 0, and regularity condition T(n) = Θ(f(n)). 22

MERGESORT ∙ Mergesort is an example of a recursive sorting algorithm. ∙ It is based on the divide-and-conquer paradigm ∙ It uses the merge operation as its fundamental component (which takes in two sorted sequences and produces a single sorted sequence) ∙ Simulation of Mergesort ∙ Drawback of mergesort: Not in-place (uses an extra temporary array) 23

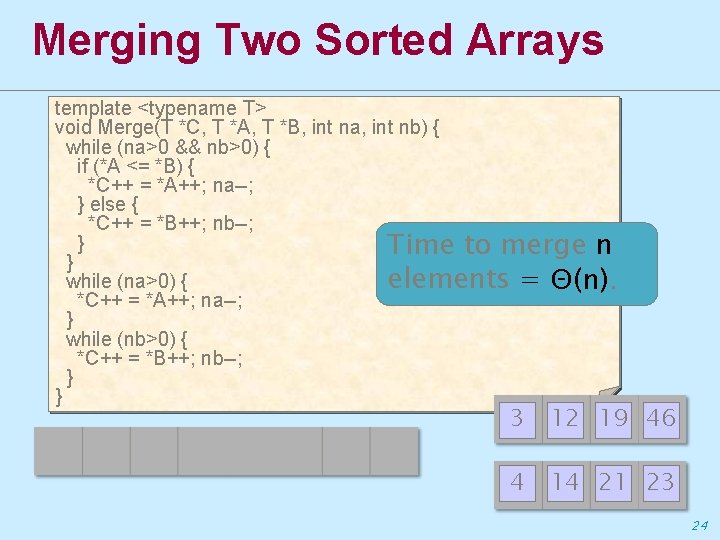
Merging Two Sorted Arrays template <typename T> void Merge(T *C, T *A, T *B, int na, int nb) { while (na>0 && nb>0) { if (*A <= *B) { *C++ = *A++; na--; } else { *C++ = *B++; nb--; } Time to merge n } while (na>0) { elements = Θ(n). *C++ = *A++; na--; } while (nb>0) { *C++ = *B++; nb--; } } 3 12 19 46 4 14 21 23 24

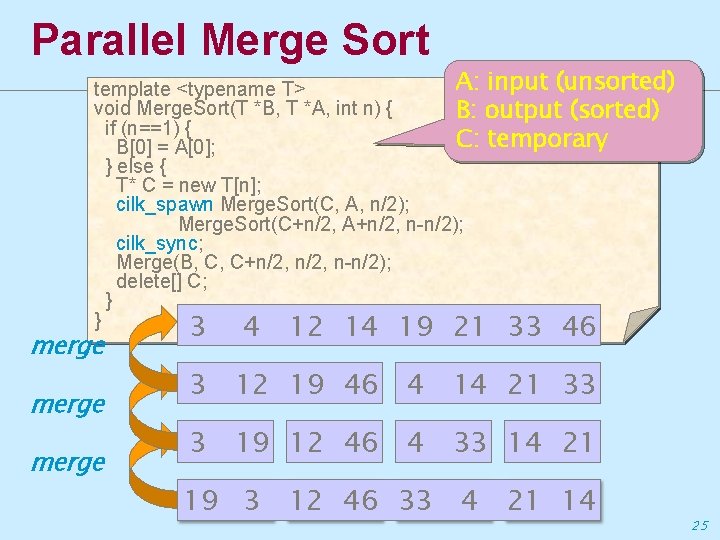
Parallel Merge Sort A: input (unsorted) template <typename T> void Merge. Sort(T *B, T *A, int n) { B: output (sorted) if (n==1) { C: temporary B[0] = A[0]; } else { T* C = new T[n]; cilk_spawn Merge. Sort(C, A, n/2); Merge. Sort(C+n/2, A+n/2, n-n/2); cilk_sync; Merge(B, C, C+n/2, n-n/2); delete[] C; } } 3 4 12 14 19 21 33 46 merge 3 12 19 46 4 14 21 33 3 19 12 46 4 33 14 21 19 3 12 46 33 4 21 14 25

Work of Merge Sort template <typename T> void Merge. Sort(T *B, T *A, int n) { if (n==1) { B[0] = A[0]; } else { T* C = new T[n]; CASE 2: cilk_spawn Merge. Sort(C, A, n/2); Merge. Sort(C+n/2, A+n/2, n-n/2); nlogba = nlog 22 = n cilk_sync; f(n) = Θ(nlogbalg 0 n) Merge(B, C, C+n/2, n-n/2); delete[] C; } } Work: T 1(n) = 2 T 1(n/2) + Θ(n) = Θ(n lg n) 26

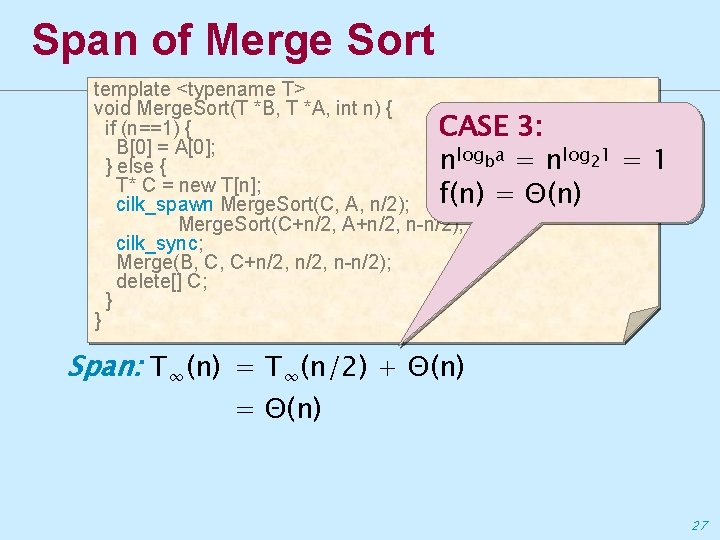
Span of Merge Sort template <typename T> void Merge. Sort(T *B, T *A, int n) { if (n==1) { CASE 3: B[0] = A[0]; nlogba = nlog 21 } else { T* C = new T[n]; cilk_spawn Merge. Sort(C, A, n/2); f(n) = Θ(n) Merge. Sort(C+n/2, A+n/2, n-n/2); cilk_sync; Merge(B, C, C+n/2, n-n/2); delete[] C; } } =1 Span: T∞(n) = T∞(n/2) + Θ(n) = Θ(n) 27

Parallelism of Merge Sort Work: T 1(n) = Θ(n lg n) Span: T∞(n) = Θ(n) Parallelism: T 1(n) T∞(n) = Θ(lg n) We need to parallelize the merge! 28

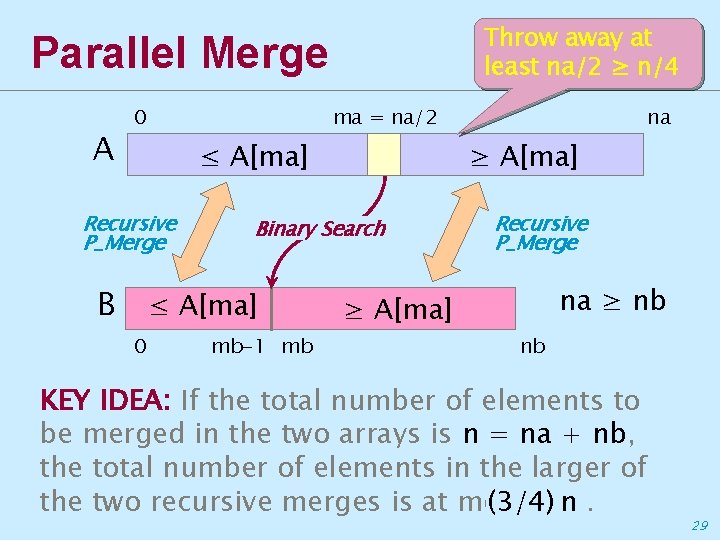
Throw away at least na/2 ≥ n/4 Parallel Merge A ma = na/2 0 ≤ A[ma] Recursive P_Merge B 0 ≥ A[ma] Binary Search ≤ A[ma] mb-1 mb na Recursive P_Merge na ≥ nb ≥ A[ma] nb KEY IDEA: If the total number of elements to be merged in the two arrays is n = na + nb, the total number of elements in the larger of the two recursive merges is at most (3/4) n. 29

Parallel Merge template <typename T> void P_Merge(T *C, T *A, T *B, int na, int nb) { if (na < nb) { P_Merge(C, B, A, nb, na); } else if (na==0) { return; } else { int ma = na/2; int mb = Binary. Search(A[ma], B, nb); C[ma+mb] = A[ma]; cilk_spawn P_Merge(C, A, B, ma, mb); P_Merge(C+ma+mb+1, A+ma+1, B+mb, na-ma-1, nb-mb); cilk_sync; } } Coarsen base cases for efficiency. 30

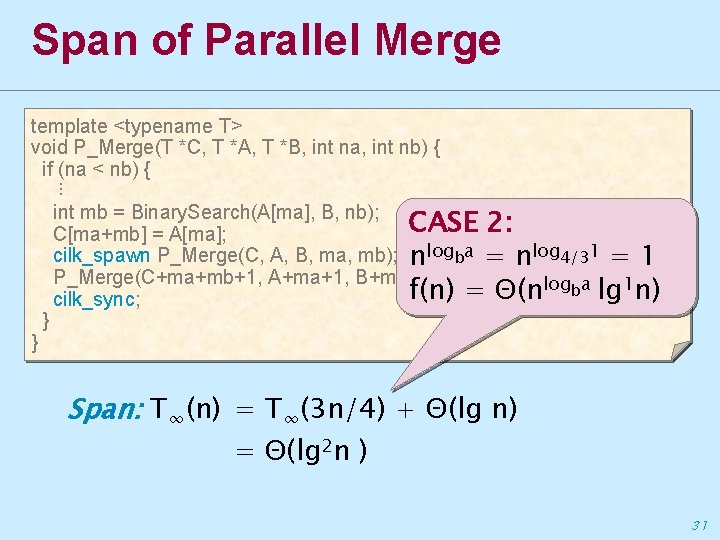
Span of Parallel Merge template <typename T> void P_Merge(T *C, T *A, T *B, int na, int nb) { if (na < nb) { ⋮ int mb = Binary. Search(A[ma], B, nb); CASE 2: C[ma+mb] = A[ma]; cilk_spawn P_Merge(C, A, B, ma, mb); nlogba = nlog 4/31 = 1 P_Merge(C+ma+mb+1, A+ma+1, B+mb, na-ma-1, nb-mb); logba lg 1 n) f(n) = Θ(n cilk_sync; } } Span: T∞(n) = T∞(3 n/4) + Θ(lg n) = Θ(lg 2 n ) 31

Work of Parallel Merge template <typename T> void P_Merge(T *C, T *A, T *B, int na, int nb) { if (na < nb) { ⋮ int mb = Binary. Search(A[ma], B, nb); C[ma+mb] = A[ma]; cilk_spawn P_Merge(C, A, B, ma, mb); P_Merge(C+ma+mb+1, A+ma+1, B+mb, na-ma-1, nb-mb); cilk_sync; } } Work: T 1(n) = T 1(αn) + T 1((1 -α)n) + Θ(lg n), where 1/4 ≤ α ≤ 3/4. Claim: T 1(n) = Θ(n). 32

Analysis of Work Recurrence Work: T 1(n) = T 1(αn) + T 1((1 -α)n) + Θ(lg n), where 1/4 ≤ α ≤ 3/4. Substitution method: Inductive hypothesis is T 1(k) ≤ c 1 k – c 2 lg k, where c 1, c 2 > 0. Prove that the relation holds, and solve for c 1 and c 2. T 1(n)=T 1( n) + T 1((1– )n) + (lg n) ≤ c 1( n) – c 2 lg( n) + c 1(1– )n – c 2 lg((1– )n) + (lg n) 33

Analysis of Work Recurrence Work: T 1(n) = T 1(αn) + T 1((1 -α)n) + Θ(lg n), where 1/4 ≤ α ≤ 3/4. T 1(n)=T 1( n) + T 1((1– )n) + (lg n) ≤ c 1( n) – c 2 lg( n) + c 1(1– )n – c 2 lg((1– )n) + (lg n) 34

Analysis of Work Recurrence Work: T 1(n) = T 1(αn) + T 1((1 -α)n) + Θ(lg n), where 1/4 ≤ α ≤ 3/4. T 1(n)=T 1( n) + T 1((1– )n) + Θ(lg n) ≤ c 1( n) – c 2 lg( n) + c 1(1– )n – c 2 lg((1– )n) + Θ(lg n) ≤ c 1 n – c 2 lg( n) – c 2 lg((1– )n) + Θ(lg n) ≤ c 1 n – c 2 ( lg( (1– )) + 2 lg n ) + Θ(lg n) ≤ c 1 n – c 2 lg n – (c 2(lg n + lg( (1– ))) – Θ(lg n)) ≤ c 1 n – c 2 lg n by choosing c 2 large enough. Choose c 1 large enough to handle the base case. 35

Parallelism of P_Merge Work: T 1(n) = Θ(n) Span: T∞(n) = Θ(lg 2 n) Parallelism: T 1(n) T∞(n) = Θ(n/lg 2 n) 36

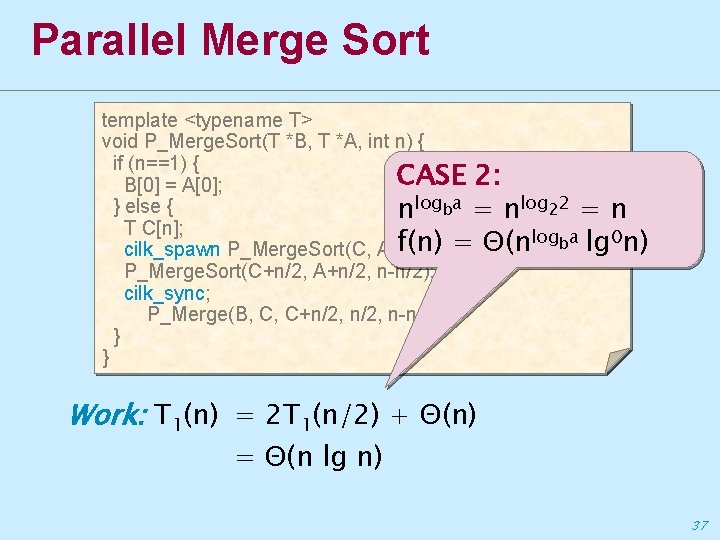
Parallel Merge Sort template <typename T> void P_Merge. Sort(T *B, T *A, int n) { if (n==1) { CASE 2: B[0] = A[0]; } else { nlogba = nlog 22 = n T C[n]; logba lg 0 n) f(n) = Θ(n cilk_spawn P_Merge. Sort(C, A, n/2); P_Merge. Sort(C+n/2, A+n/2, n-n/2); cilk_sync; P_Merge(B, C, C+n/2, n-n/2); } } Work: T 1(n) = 2 T 1(n/2) + Θ(n) = Θ(n lg n) 37

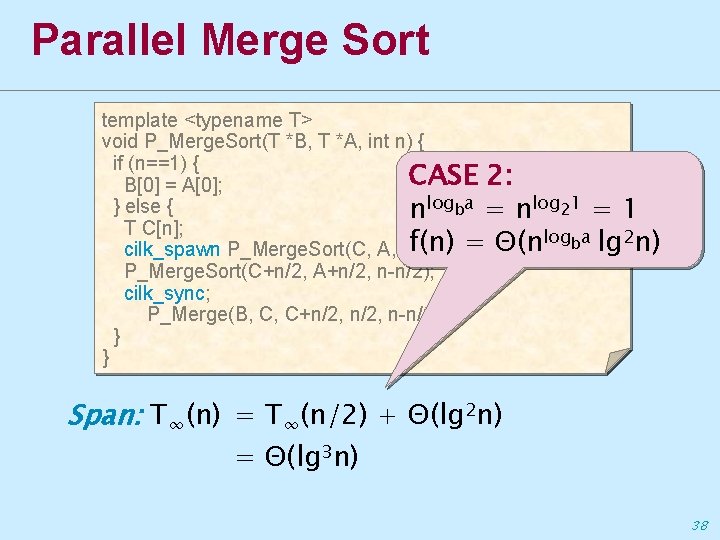
Parallel Merge Sort template <typename T> void P_Merge. Sort(T *B, T *A, int n) { if (n==1) { CASE 2: B[0] = A[0]; } else { nlogba = nlog 21 = 1 T C[n]; logba lg 2 n) f(n) = Θ(n cilk_spawn P_Merge. Sort(C, A, n/2); P_Merge. Sort(C+n/2, A+n/2, n-n/2); cilk_sync; P_Merge(B, C, C+n/2, n-n/2); } } Span: T∞(n) = T∞(n/2) + Θ(lg 2 n) = Θ(lg 3 n) 38

Parallelism of P_Merge. Sort Work: T 1(n) = Θ(n lg n) Span: T∞(n) = Θ(lg 3 n) Parallelism: T 1(n) T∞(n) = Θ(n/lg 2 n) 39