Scientific Measurement QUALITATIVE VS QUANTITATIVE QUALITATIVE DESCRIPTIVE NONNUMERICAL

























- Slides: 31

Scientific Measurement: QUALITATIVE VS. QUANTITATIVE QUALITATIVE = DESCRIPTIVE, NONNUMERICAL. EX. : THE MORNINGS ARE GETTING VERY COLD. QUANTITATIVE = NUMERICAL, DEFINITE MEASUREMENT EX. : THE TEMPERATURE WAS 65°F THIS MORNING.

Scientific Measurement: Metric Know your metric relationships! kilo -hecta - deca -(base) - deci - centi – milli ( 103 - 102 -101 - (1) – 10 -1 - 10 -2 - 10 -3) King Henry Died By Drinking Chocolate Milk

Scientific Notation In science, we deal with some very LARGE numbers: 1 mole = 60200000000000 In science, we deal with some very SMALL numbers: Mass of an electron = 0. 000000000000000091 kg

Imagine the difficulty of calculating the mass of 1 mole of electrons! 0. 000000000000000091 kg x 60200000000000 ? ? ? ? ? ? ? ? ?

Scientific Notation: A method of representing very large or very small numbers in the form: M x 10 n ØM is a number between 1 and 10 Ø n is an integer

2 500 000 9 8 7 6 5 4 3 Step #1: Insert an understood decimal point Step #2: Decide where the decimal must end up so that one number is to its left Step #3: Count how many places you bounce the decimal point Step #4: Re-write in the form M x 10 n 2 . 1

2. 5 x 9 10 The exponent is the number of places we moved the decimal.

0. 0000579 1 2 3 4 5 Step #2: Decide where the decimal must end up so that one number is to its left Step #3: Count how many places you bounce the decimal point Step #4: Re-write in the form M x 10 n

5. 79 x -5 10 The exponent is negative because the number we started with was less than 1.

Scientific Notation Rules for using scientific notation Numbers are represented as a value between 1 <10 Exponents (+) (-) Ex: (+), (-) describe the decimal movement number grows larger number gets smaller 1. 2 x 10 3 = 1200 Math function and scientific notation: Be sure to use the [2 nd][EE] function on your calculator! Ex. 5. 03 x 1014 / 2. 9 x 107 = ?

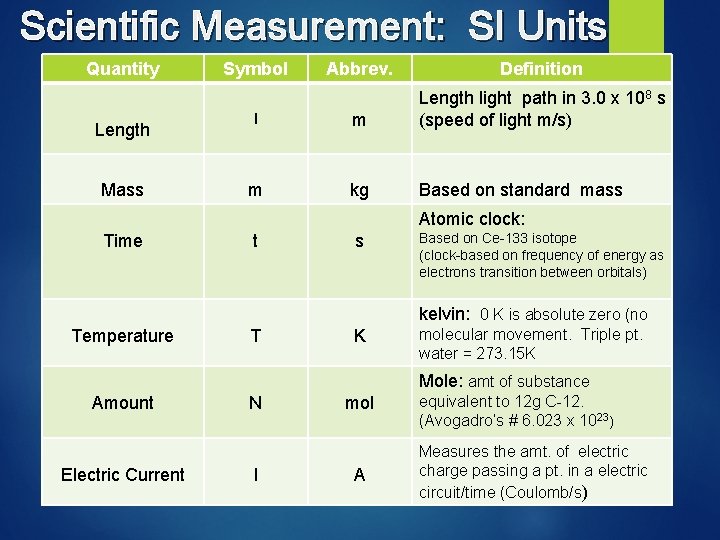
Scientific Measurement: SI Units Standard Unit of measure Metric based measurements Length = meter (m) Mass = kilograms (kg) Time = seconds (s) Temperature = Kelvin (K) Amount of substance = mole (mol) Electric Current = ampere (A)

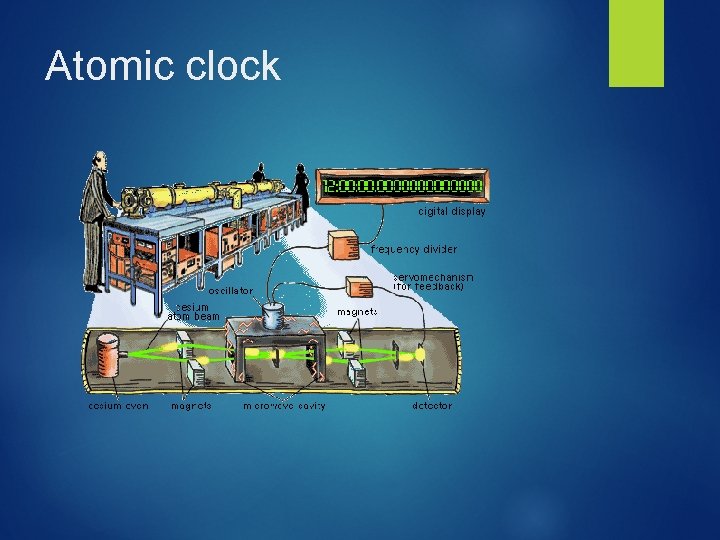
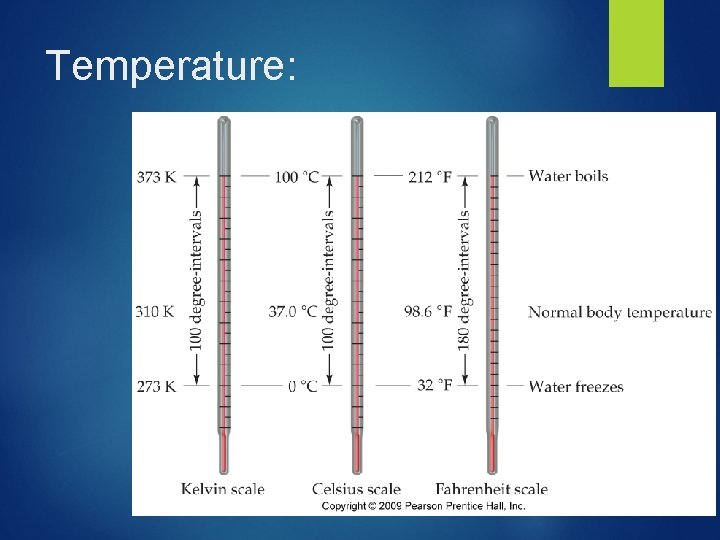
Scientific Measurement: SI Units Quantity Length Mass Symbol Abbrev. Definition l m Length light path in 3. 0 x 108 s (speed of light m/s) m kg Based on standard mass Atomic clock: Time t s Based on Ce-133 isotope (clock-based on frequency of energy as electrons transition between orbitals) kelvin: 0 K is absolute zero (no Temperature T K molecular movement. Triple pt. water = 273. 15 K Mole: amt of substance Amount Electric Current N l mol A equivalent to 12 g C-12. (Avogadro’s # 6. 023 x 1023) Measures the amt. of electric charge passing a pt. in a electric circuit/time (Coulomb/s)

Atomic clock

Temperature:

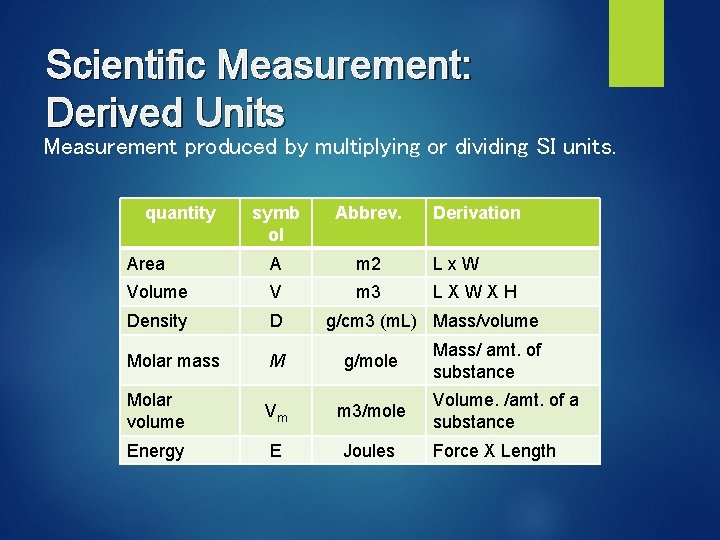
Scientific Measurement: Derived Units Measurement produced by multiplying or dividing SI units. quantity symb ol Abbrev. Derivation Area A m 2 Lx. W Volume V m 3 LXWXH Density D Molar mass M g/mole Molar volume Vm m 3/mole Energy E Joules g/cm 3 (m. L) Mass/volume Mass/ amt. of substance Volume. /amt. of a substance Force X Length

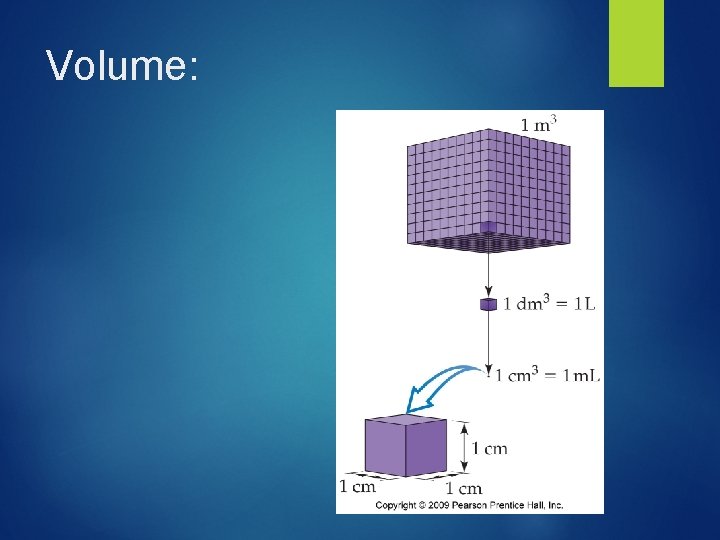
Volume Measurement The amount of space occupied by an object Some useful relationships: 1 Liter = 1 dm 3 = 103 cm 3 = 1000 m. L 1 cm 3 = 1 m. L

Volume:

Density Measurement Describes the ratio of mass to volume Density is a physical property that is independent to amount (intensive property) D = Mass/Volume= (g/m. L or g/cm 3)

Measuring density: Solids - Liquids Displacement

Calculations using density: Conversions using density: Ex. Aluminum has a density of 2. 699 g/cm 3 What is mass of a 11. 25 cm 3 block of Al? 11. 25 cm 3 2. 699 g 1 cm 3 = 30. 36 g Al What is the volume of a 3. 75 g sample of Al? 3. 75 g Al 1 cm 3 = 1. 38 cm 3 2. 699 g

Conversion Factors A relationship showing the equality between two different units that allows for conversion between these units. Examples: 1 week = 7 days 1 dozen eggs = 12 eggs ? ? ?

Scientific Measurement: Accuracy- close to the true value Precision- close within measurements % Error- describes how close your data is to the accepted value Accepted – Experimental x 100 Accepted Value

Accuracy & Precision

Scientific Measurement: Significant Figures Used to express the accuracy of a number. Used for “measured” numbers. Rules for determining Sig. Figs. 1. All non-zero numbers are significant 2. Captive zeros are significant 3. Leading zeros are not significant 4. Trailing zeros are significant if a decimal is present

Significant figures: Determine the number of sig figs 1. 3060 2. . 000789 3. 1. 40 x 10 6 4. 1000 5. 2030. 6. 45, 0060

Answers: Determine the number of sig figs 1. 3060 (3) 2. . 000789 (3) 3. 1. 40 x 10 6 (3) 4. 1000 (1) 5. 2030. 6. 45, 0060 (4) (5)

Calculations using Significant Figures Addition/Subtraction Limited to the placement of the least significant figure. ex. 12. 00 + 8. 3 + 14 = Multiplication/Division Limited to the lowest number of significant figures. Ex. 12. 0 x 8. 3 X 14 =

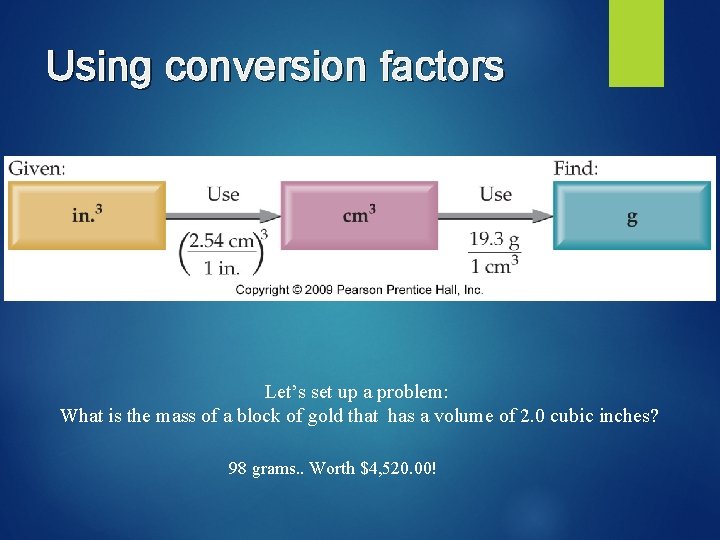
Using conversion factors Let’s set up a problem: What is the mass of a block of gold that has a volume of 2. 0 cubic inches? 98 grams. . Worth $4, 520. 00!

Problem Solving Steps to Problem Solving Approach: A. Analyze: determine starting point and plan steps required to get a solution (unknown). B. Plan: set up a strategy to solve the problem. C. Solve: conduct appropriate calculations based on plan. This may require multiple steps. D. Evaluate: Review answer to see if it seems reasonable.

Problem Solving a ratio of equivalent measurements ( 1 inch = 2. 54 cm) Conversion Factors- Dimensional Analysis- the technique for solving problems using unit conversions based on conversion factors Ex. 6. 42 inches = ? cm

Problem Solving Multi-step Problems – use more than one conversion factor: ex. 5 days = ? minutes Complex Problems- involves ratios of two units: ex. . 45 Km/hrs = ? m/s Golden Rule for conversions…always show your work!
 Examples of qualitative data
Examples of qualitative data Research design descriptive quantitative
Research design descriptive quantitative Research design approach
Research design approach The kinds of quantitative research
The kinds of quantitative research Quantitative descriptive method
Quantitative descriptive method 間斷變數
間斷變數 Qualitative variables and quantitative variables
Qualitative variables and quantitative variables Qualitative and quantitative
Qualitative and quantitative Qualitative research methods
Qualitative research methods Qualitative and quantitative test for lipids
Qualitative and quantitative test for lipids Qualitative vs quantitative science
Qualitative vs quantitative science Qualitative traits vs quantitative traits
Qualitative traits vs quantitative traits Qualitative vs quantitative sociology
Qualitative vs quantitative sociology Integrating qualitative and quantitative methods
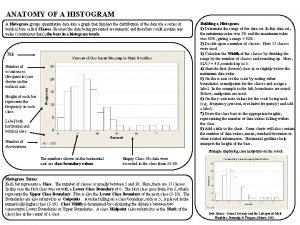
Integrating qualitative and quantitative methods Is a histogram qualitative or quantitative
Is a histogram qualitative or quantitative Qualitative vs quantitative political science
Qualitative vs quantitative political science Qualitative vs quantitative
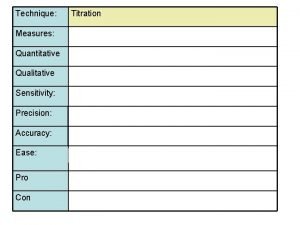
Qualitative vs quantitative Is titration qualitative or quantitative
Is titration qualitative or quantitative Qualitative researcch has holistic nature
Qualitative researcch has holistic nature Words images objects qualitative or quantitative
Words images objects qualitative or quantitative Quantitative und qualitative differenzierung
Quantitative und qualitative differenzierung Quantitative qualitative estimation
Quantitative qualitative estimation Qualitative vs quantitative measurements
Qualitative vs quantitative measurements Quantitative observation definition
Quantitative observation definition Quantitative observations
Quantitative observations Qualitative vs quantitative data analysis
Qualitative vs quantitative data analysis Similarities between qualitative and quantitative research
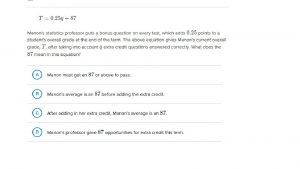
Similarities between qualitative and quantitative research In a survey of 177 237 u.s. adults
In a survey of 177 237 u.s. adults Quantitative vs qualitative observations
Quantitative vs qualitative observations Inheritance of quantitative traits
Inheritance of quantitative traits Sampling methods in qualitative and quantitative research
Sampling methods in qualitative and quantitative research Similarities of qualitative and quantitative research
Similarities of qualitative and quantitative research