Module 2 Divide and Conquer Divide and Conquer






![Quick sort • ALGORITHM Quicksort(A[l. . r]) • //Sorts a subarray by quicksort • Quick sort • ALGORITHM Quicksort(A[l. . r]) • //Sorts a subarray by quicksort •](https://slidetodoc.com/presentation_image_h/93a23f0f4de37029036c7e6ec2dbc4cd/image-8.jpg)
![ALGORITHM : Partition(A[l. . r]) //Partitions a subarray by Hoare’s algorithm, using the first ALGORITHM : Partition(A[l. . r]) //Partitions a subarray by Hoare’s algorithm, using the first](https://slidetodoc.com/presentation_image_h/93a23f0f4de37029036c7e6ec2dbc4cd/image-9.jpg)

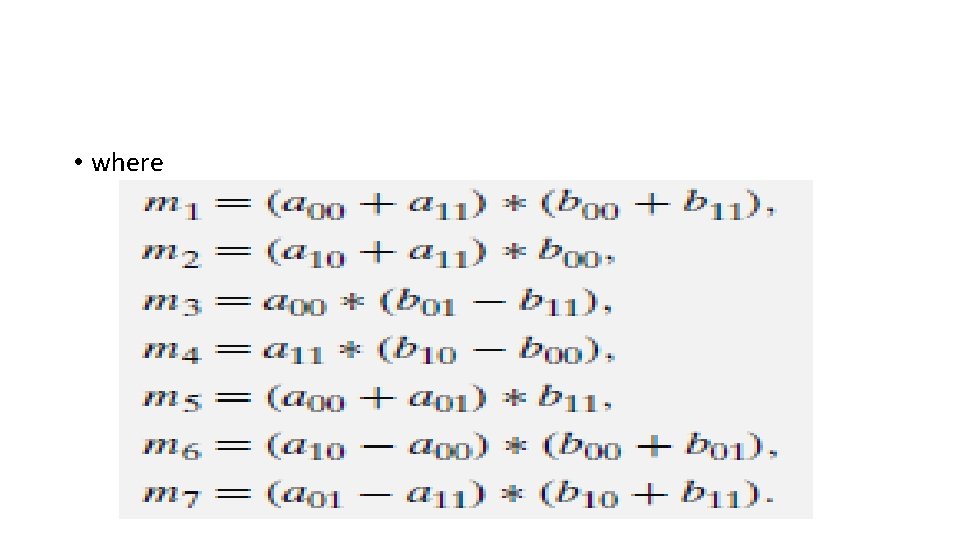





- Slides: 17

Module 2: Divide and Conquer

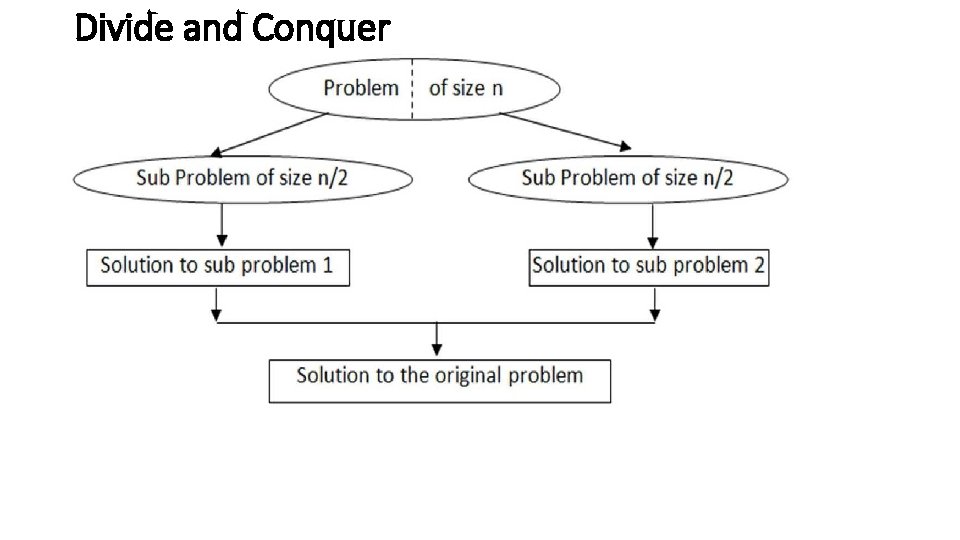
Divide and Conquer

Algorithm DAnd. C(P) {. if Small(P) Then return S(P); else { divide P into smaller instances P 1, P 2, . . . , Pn, n>1; Apply DAnd. C t, o each of these subproblems; return Combine(DAnd. C(P 1), DAnd. C(P 2), DAnd. C(Pn)); } }

Solving recurrence relation using Master theorem • It states that, in recurrence equation T(n) = a. T(n/b) + f(n), • If f(n)∈ Θ (nd ) where d ≥ 0 then



![Quick sort ALGORITHM QuicksortAl r Sorts a subarray by quicksort Quick sort • ALGORITHM Quicksort(A[l. . r]) • //Sorts a subarray by quicksort •](https://slidetodoc.com/presentation_image_h/93a23f0f4de37029036c7e6ec2dbc4cd/image-8.jpg)
Quick sort • ALGORITHM Quicksort(A[l. . r]) • //Sorts a subarray by quicksort • //Input: Subarray of array A[0. . n − 1], defined by its left and right • // indices l and r • //Output: Subarray A[l. . r] sorted in nondecreasing order • if l < r • s ←Partition(A[l. . r]) //s is a split position • Quicksort(A[l. . s − 1]) • Quicksort(A[s + 1. . r])
![ALGORITHM PartitionAl r Partitions a subarray by Hoares algorithm using the first ALGORITHM : Partition(A[l. . r]) //Partitions a subarray by Hoare’s algorithm, using the first](https://slidetodoc.com/presentation_image_h/93a23f0f4de37029036c7e6ec2dbc4cd/image-9.jpg)
ALGORITHM : Partition(A[l. . r]) //Partitions a subarray by Hoare’s algorithm, using the first element // as a pivot //Input: Subarray of array A[0. . n − 1], defined by its left and right // indices l and r (l<r) //Output: Partition of A[l. . r], with the split position returned as // this function’s value p←A[l] i ←l; j ←r + 1 repeat i ←i + 1 until A[i]≥ p repeat j ←j − 1 until A[j ]≤ p swap(A[i], A[j ]) until i ≥ j swap(A[i], A[j ]) //undo last swap when i ≥ j swap(A[l], A[j ]) return j

Analysis • Cbest(n) = 2 Cbest(n/2) + n for n > 1, Cbest(1) = 0. • According to the Master Theorem, Cbest(n) ∈ (n log 2 n); solving it exactly for n = 2 k yields Cbest(n) = n log 2 n. • Cworst(n) = (n + 1) + n +. . . + 3 = ((n + 1)(n + 2))/2− 3 ∈ (n 2). • .

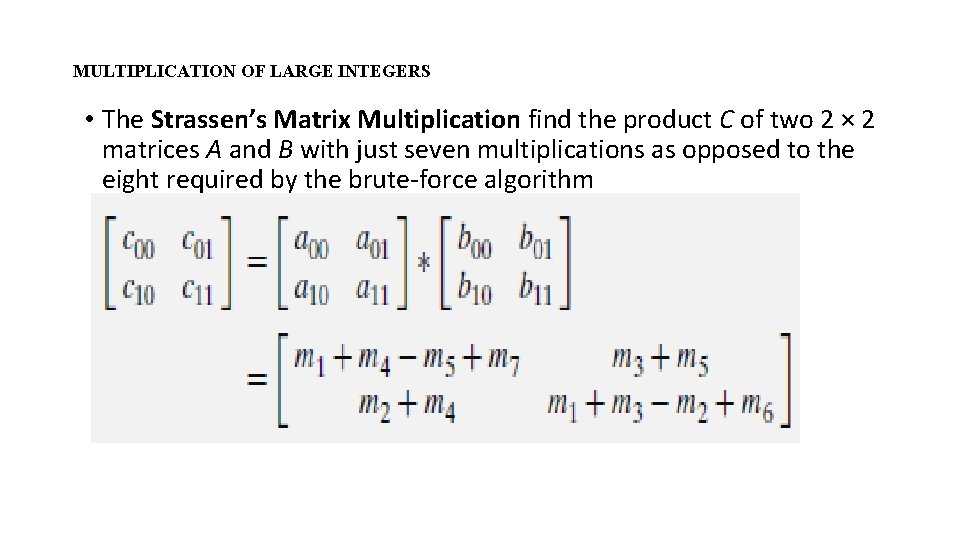
MULTIPLICATION OF LARGE INTEGERS • The Strassen’s Matrix Multiplication find the product C of two 2 × 2 matrices A and B with just seven multiplications as opposed to the eight required by the brute-force algorithm
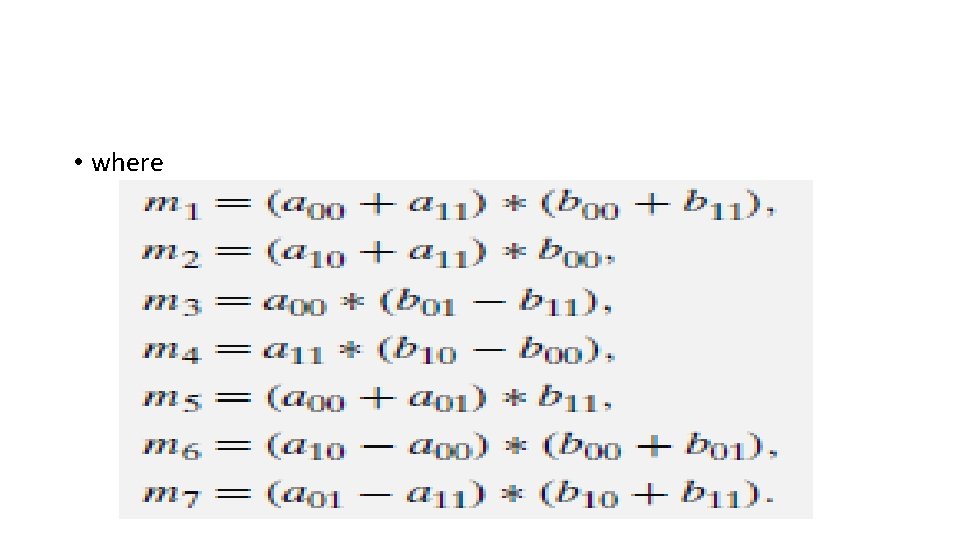
• where

The asymptotic efficiency of Strassen’s matrix multiplication algorithm • If M(n) is the number of multiplications made by Strassen’s algorithm in multiplying two n×n matrices, where n is a power of 2, The recurrence relation is M(n) = 7 M(n/2) for n > 1, M(1)=1. Since n = 2 k, M(2 k) = 7 M(2 k− 1) = 7[7 M(2 k− 2)] = 72 M(2 k− 2) =. . .


Finding the Maximum and Minum


Analysis