CRYPTOGRAPHIC PROTOCOLS 2015 LECTURE 5 twomessage homomorphic protocols

CRYPTOGRAPHIC PROTOCOLS 2015, LECTURE 5 two-message homomorphic protocols Helger Lipmaa University of Tartu, Estonia

UP TO NOW Assumptions, reductions DL, CDH, DDH Key exchange Modularization, Elgamal

THIS TIME This time: secure computation Concrete two-message protocols Some of them are toy, some are useful Note: here Enc will denote lifted Elgamal

FUNCTIONALITY a a ∈ S₁ b ∈ S₂ fₐ(a, b) Goal

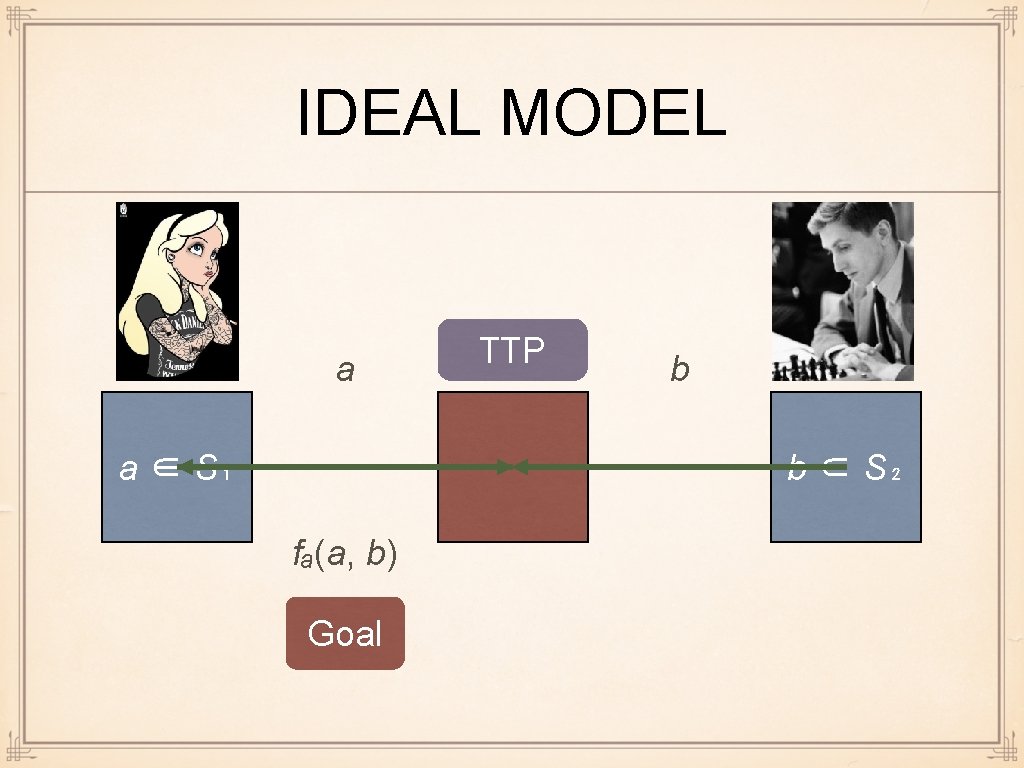
IDEAL MODEL a a ∈ S₁ TTP b b ∈ S₂ fₐ(a, b) Goal

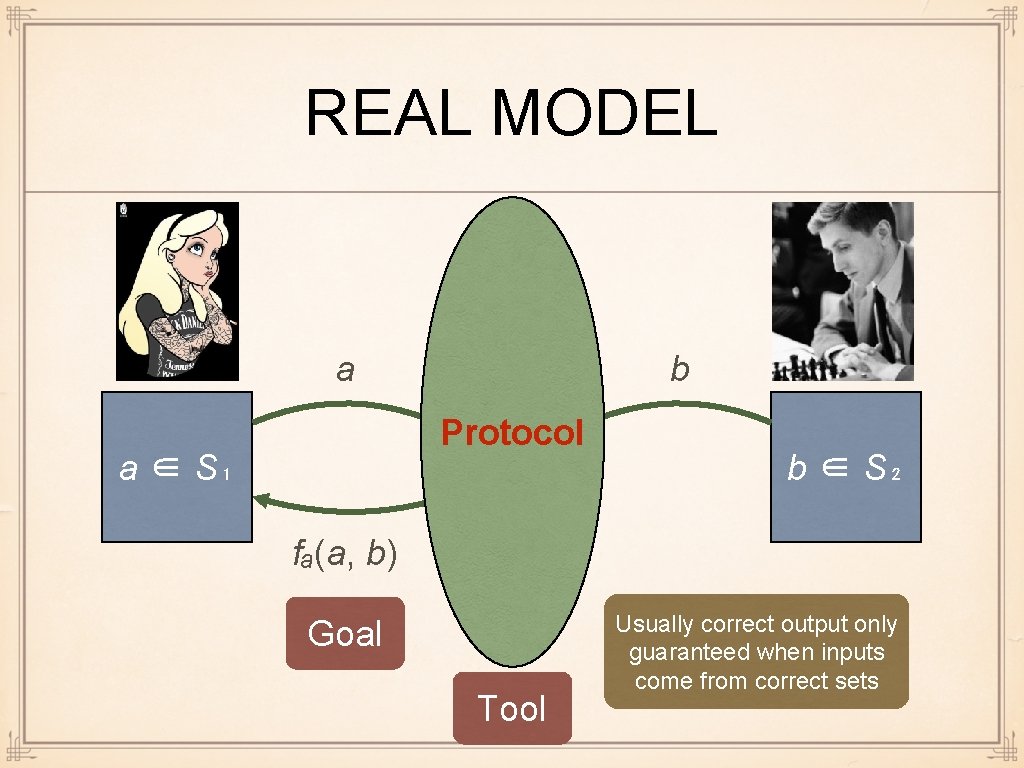
REAL MODEL a b Protocol a ∈ S₁ b ∈ S₂ fₐ(a, b) Goal Tool Usually correct output only guaranteed when inputs come from correct sets

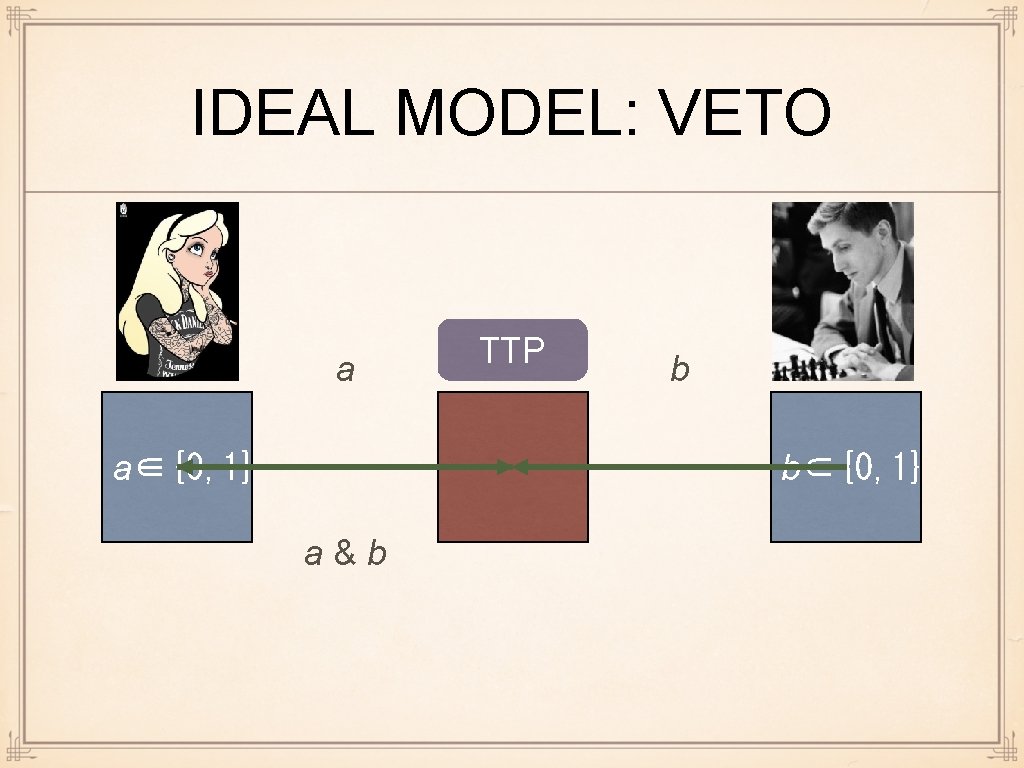
IDEAL MODEL: VETO a a∈{0, 1} TTP b b∈{0, 1} a&b

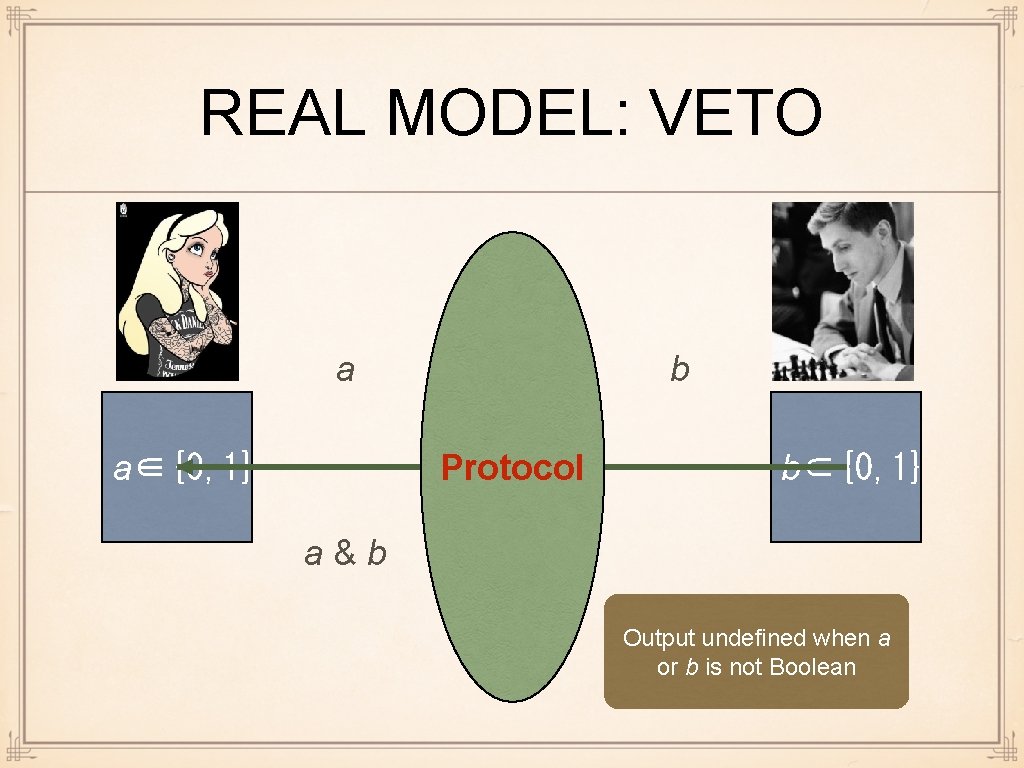
REAL MODEL: VETO a TTP Protocol a∈{0, 1} b b∈{0, 1} a&b Output undefined when a or b is not Boolean

FUNCTIONALITY VS PROTOCOL (a, a & b) leaks something about b This is a problem of the functionality, not of the protocol If leaking is not desired, redefine the functionality! Some functionalities just do not exist Goal: functionality Tool: cryptography a 0 0 1 1 b 0 1 a&b 0 0 0 1

IDEA: LINEARIZATION Lifted Elgamal enables to compute linear function Linearization: transform given non-linear function f into a linear function f * that agrees with f on restricted input set Example: a & b = a · b for a, b ∈ {0, 1}

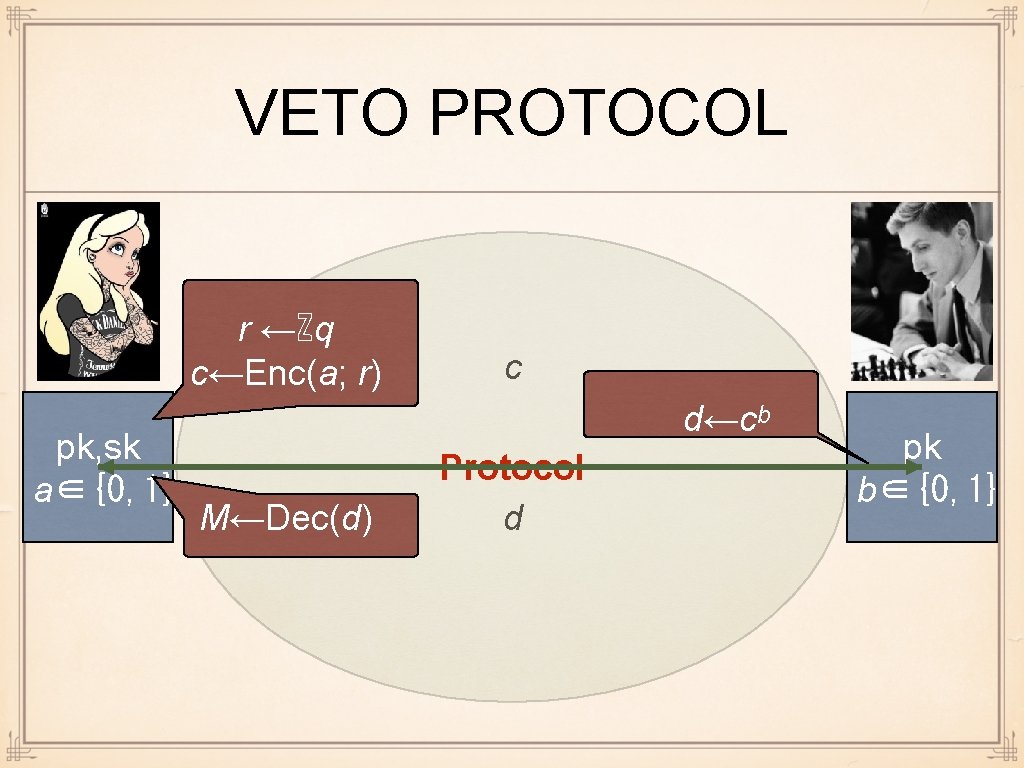
VETO PROTOCOL r ←ℤq c←Enc(a; r) pk, sk a∈{0, 1} c d←cᵇ M←Dec(d) Protocol d pk b∈{0, 1}

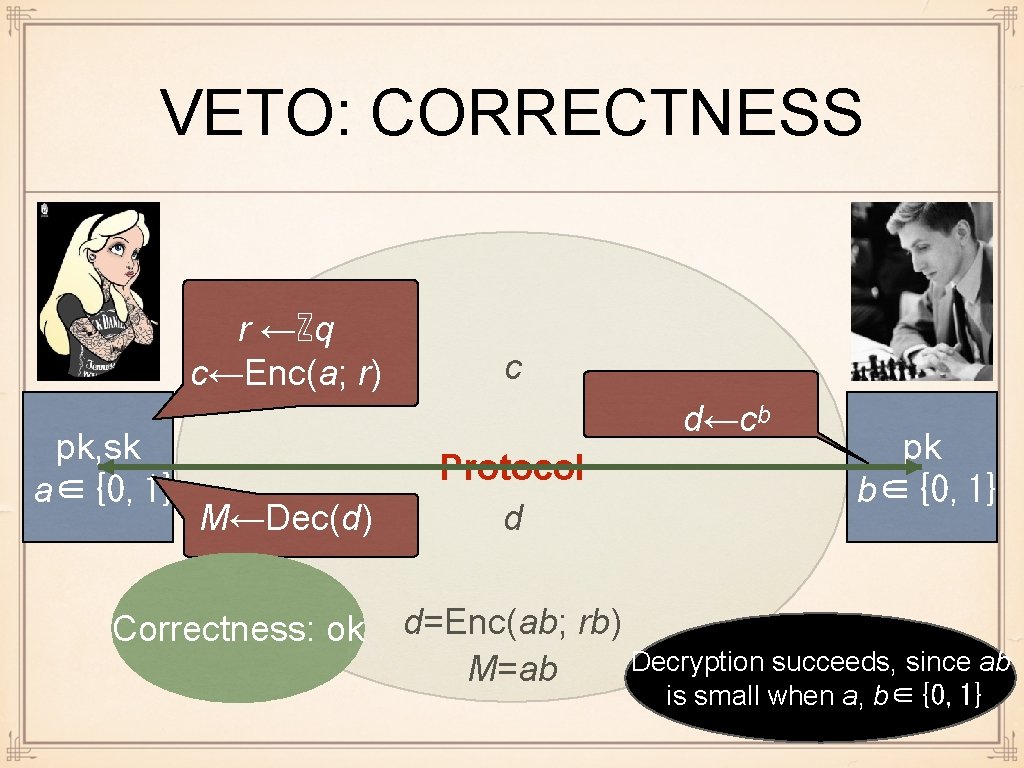
VETO: CORRECTNESS r ←ℤq c←Enc(a; r) pk, sk a∈{0, 1} c d←cᵇ M←Dec(d) Correctness: ok Protocol d pk b∈{0, 1} d=Enc(ab; rb) Decryption succeeds, since ab M=ab is small when a, b∈{0, 1}

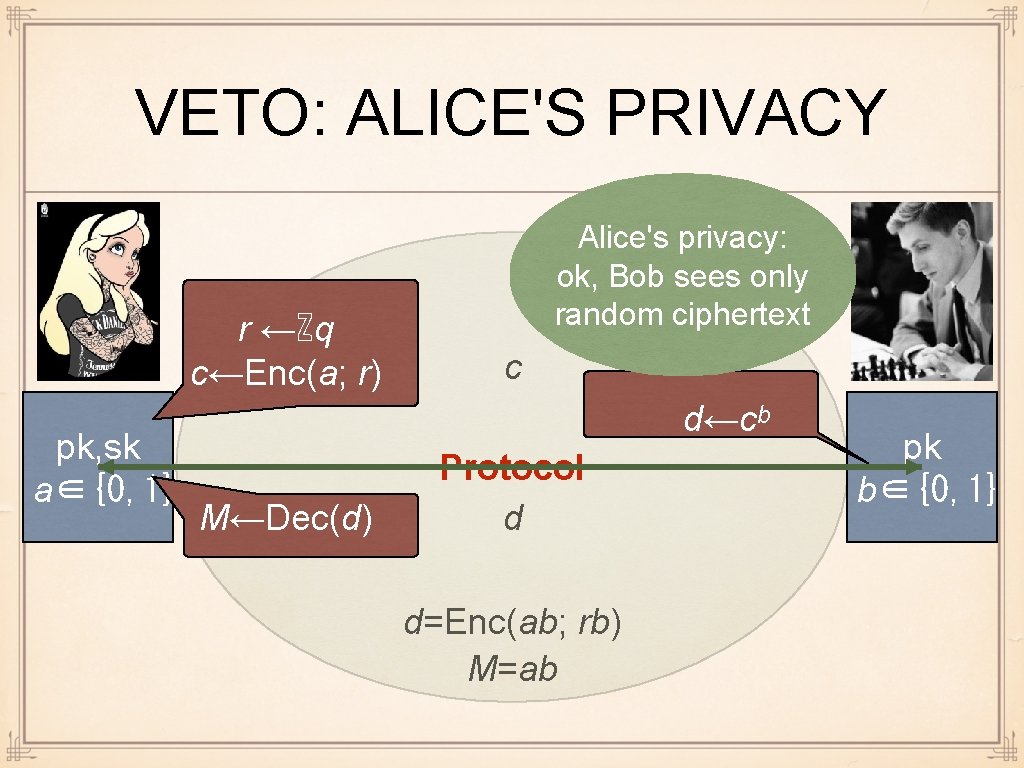
VETO: ALICE'S PRIVACY r ←ℤq c←Enc(a; r) pk, sk a∈{0, 1} Alice's privacy: ok, Bob sees only random ciphertext c d←cᵇ M←Dec(d) Protocol d d=Enc(ab; rb) M=ab pk b∈{0, 1}

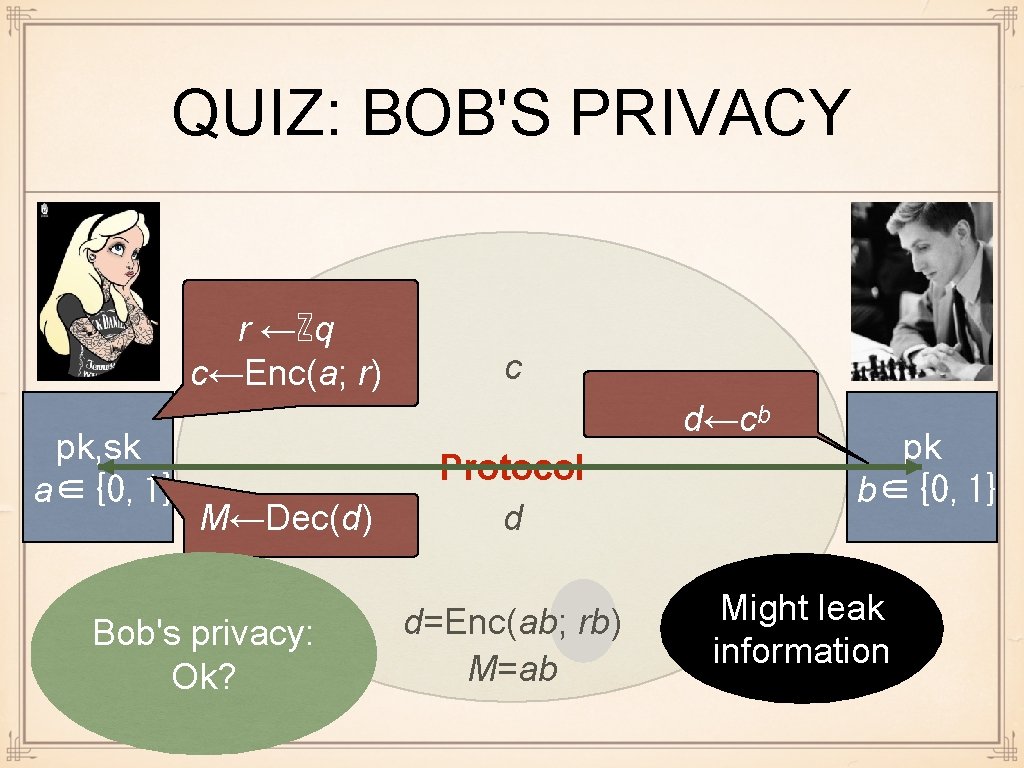
QUIZ: BOB'S PRIVACY r ←ℤq c←Enc(a; r) pk, sk a∈{0, 1} c d←cᵇ M←Dec(d) Bob's privacy: Ok? Protocol d d=Enc(ab; rb) M=ab pk b∈{0, 1} Might leak information

BLINDING PROPERTY Enc(m; r) · Enc(0; r') = Enc(m; r + r') follows from the definition of (lifted) Elgamal r' random => r + r' random for any r Blinding property: given any encryption of (unknown) m => can compute random encryption of m

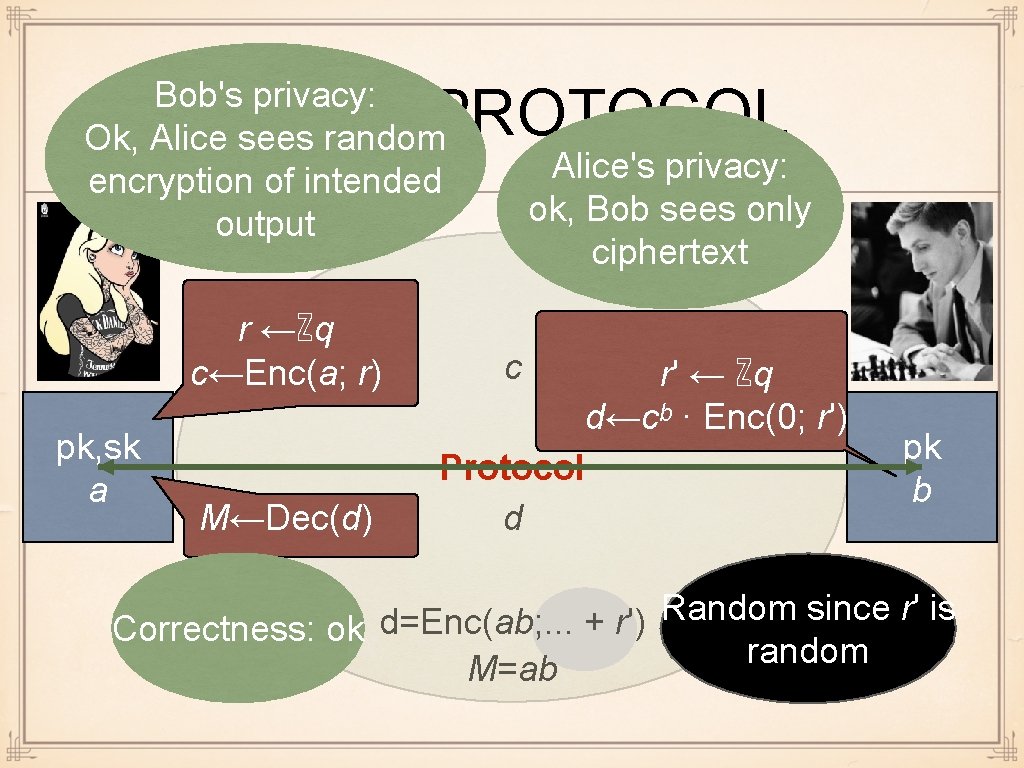
Bob's privacy: Ok, Alice sees random encryption of intended output VETO PROTOCOL r ←ℤq c←Enc(a; r) pk, sk a M←Dec(d) Alice's privacy: ok, Bob sees only ciphertext c Protocol d r' ← ℤq d←cᵇ · Enc(0; r') pk b Random since r' is d=Enc(ab; . . . + r') Correctness: ok random M=ab

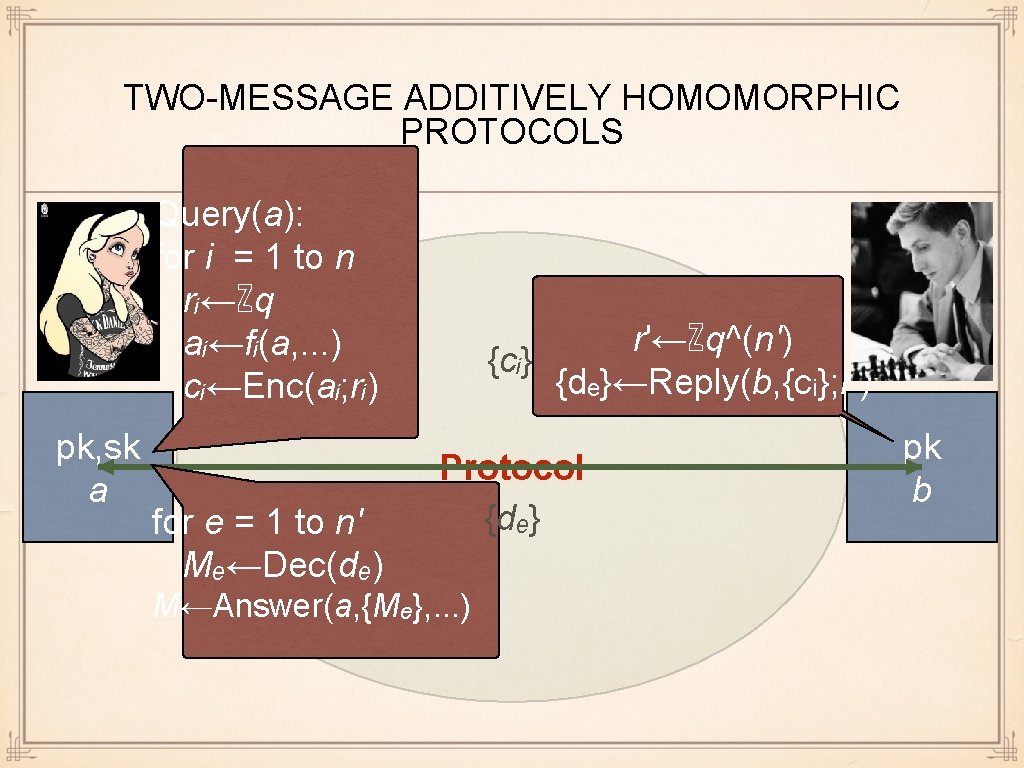
TWO-MESSAGE ADDITIVELY HOMOMORPHIC PROTOCOLS Query(a): for i = 1 to n rᵢ←ℤq aᵢ←fᵢ(a, . . . ) cᵢ←Enc(aᵢ; rᵢ) pk, sk a for e = 1 to n' Mₑ←Dec(dₑ) r'←ℤq^(n') {cᵢ} {dₑ}←Reply(b, {cᵢ}; r') Protocol {dₑ} M←Answer(a, {Mₑ}, . . . ) pk b

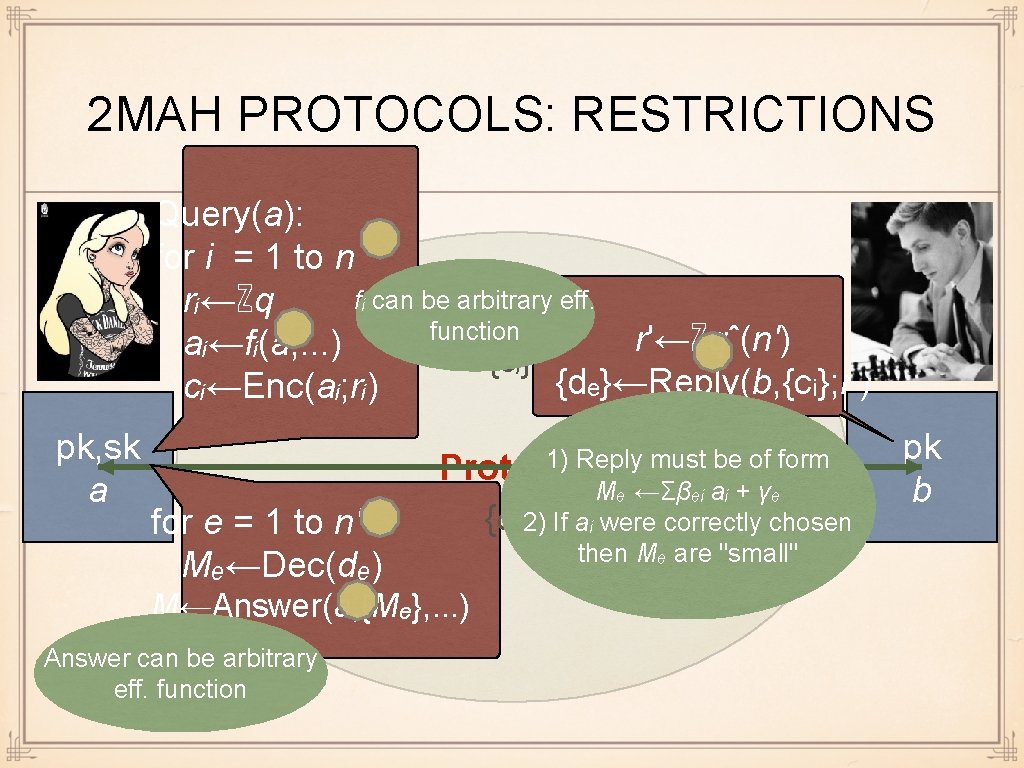
2 MAH PROTOCOLS: RESTRICTIONS Query(a): for i = 1 to n fᵢ can be arbitrary eff. rᵢ←ℤq function r'←ℤqˆ(n') aᵢ←fᵢ(a, . . . ) {cᵢ} {dₑ}←Reply(b, {cᵢ}; r') cᵢ←Enc(aᵢ; rᵢ) pk, sk a for e = 1 to n' Mₑ←Dec(dₑ) 1) Reply must be of form Protocol Mₑ ←Σβₑᵢ aᵢ + γₑ {dₑ} 2) If aᵢ were correctly chosen then Mₑ are "small" M←Answer(a, {Mₑ}, . . . ) Answer can be arbitrary eff. function pk b

FUNCTIONALITY: SCALAR PRODUCT a aᵢ∈{0, 1}ᴸ a={aᵢ: i∈[n]} TTP Protocol <a, b>=Σaᵢbᵢ b bᵢ∈{0, 1}ᴸ b={bᵢ: i∈[n]}

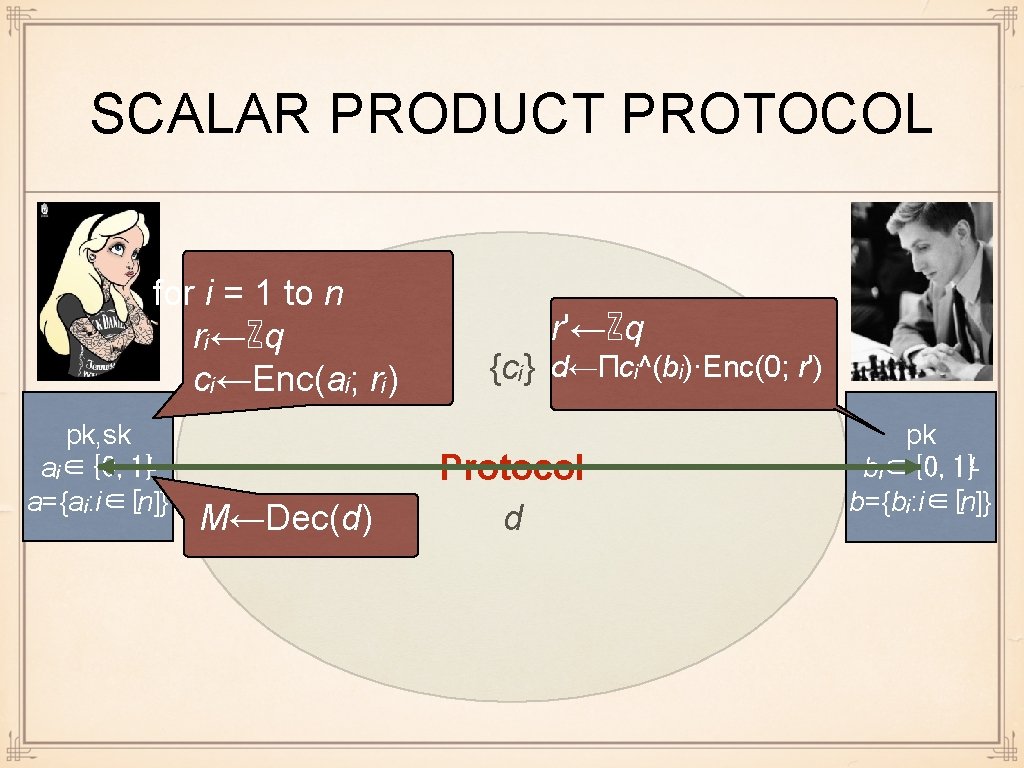
SCALAR PRODUCT PROTOCOL for i = 1 to n rᵢ←ℤq cᵢ←Enc(aᵢ; rᵢ) pk, sk aᵢ∈{0, 1}ᴸ a={aᵢ: i∈[n]} M←Dec(d) r'←ℤq {cᵢ} d←Πcᵢ^(bᵢ)·Enc(0; r') Protocol d pk bᵢ∈{0, 1}ᴸ b={bᵢ: i∈[n]}

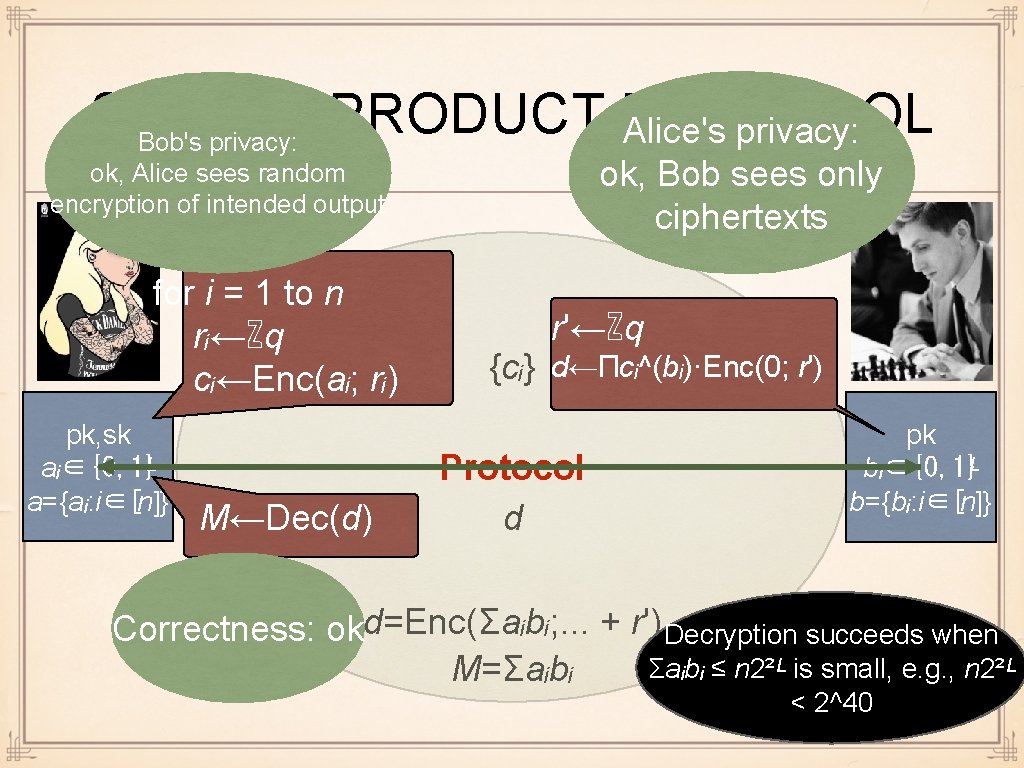
SCALAR PRODUCT PROTOCOL Alice's privacy: Bob's privacy: ok, Bob sees only ciphertexts ok, Alice sees random encryption of intended output for i = 1 to n rᵢ←ℤq cᵢ←Enc(aᵢ; rᵢ) pk, sk aᵢ∈{0, 1}ᴸ a={aᵢ: i∈[n]} M←Dec(d) r'←ℤq {cᵢ} d←Πcᵢ^(bᵢ)·Enc(0; r') Protocol d pk bᵢ∈{0, 1}ᴸ b={bᵢ: i∈[n]} Correctness: okd=Enc(Σaᵢbᵢ; . . . + r') Decryption succeeds when Σaᵢbᵢ ≤ n 2²ᴸ is small, e. g. , n 2²ᴸ M=Σaᵢbᵢ < 2^40

MORE FUN. . . Veto and scalar product are "linear" functions. . . thus straightforward to implement by using lifted Elgamal It comes out we can also implement less straightforward functionalities

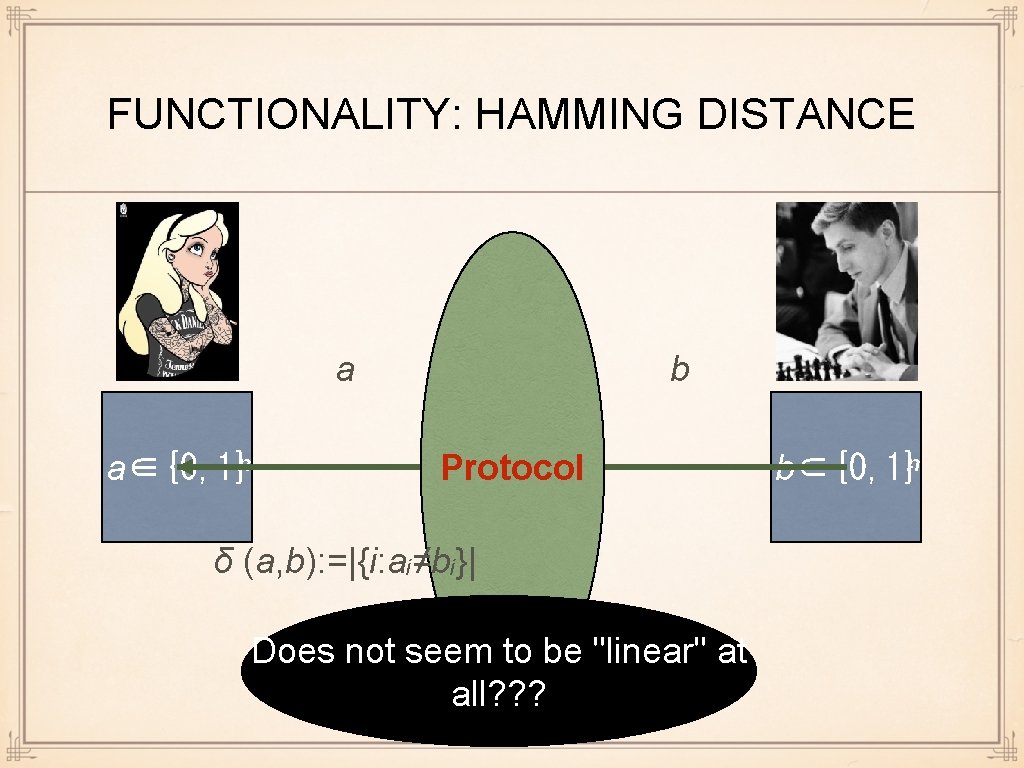
FUNCTIONALITY: HAMMING DISTANCE TTP a a∈{0, 1}ⁿ b Protocol δ (a, b): =|{i: aᵢ≠bᵢ}| Does not seem to be "linear" at all? ? ? b∈{0, 1}ⁿ

QUIZ: LINEARIZATION OF HD Note aᵢ and bᵢ are Boolean! aᵢ ≠ bᵢ iff aᵢ XOR bᵢ = 1 Moreover, Bob knows bᵢ x XOR 0 = x = 0 + (1 - 2 · 0) x x XOR 1 = 1 - x = 1 + (1 - 2 · 1) x δ is "linear" and thus we can construct 2 MAH protocol for Hamming distance x XOR y = y + (1 - 2 y) x δ (a, b) = Σᵢ (bᵢ + (1 - 2 bᵢ) aᵢ) = Σᵢ (1 - 2 bᵢ) aᵢ + Σᵢ bᵢ

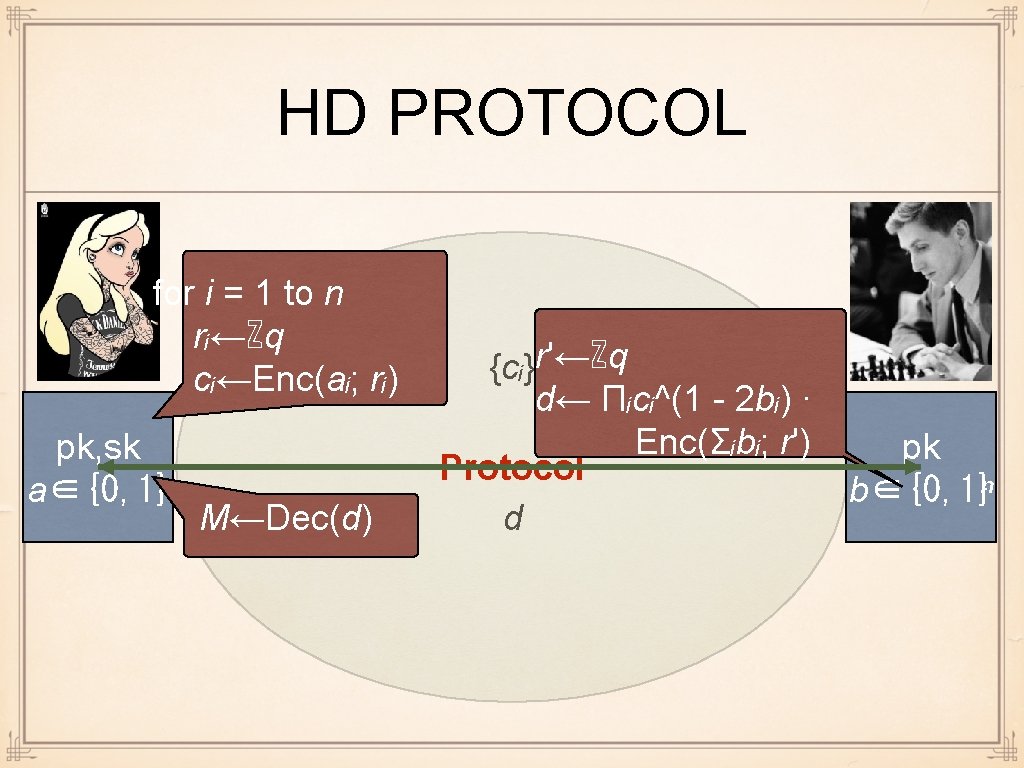
HD PROTOCOL for i = 1 to n rᵢ←ℤq cᵢ←Enc(aᵢ; rᵢ) pk, sk a∈{0, 1}ⁿ M←Dec(d) {cᵢ}r'←ℤq d← Πᵢcᵢ^(1 - 2 bᵢ) · Enc(Σᵢbᵢ; r') pk Protocol b∈{0, 1}ⁿ d

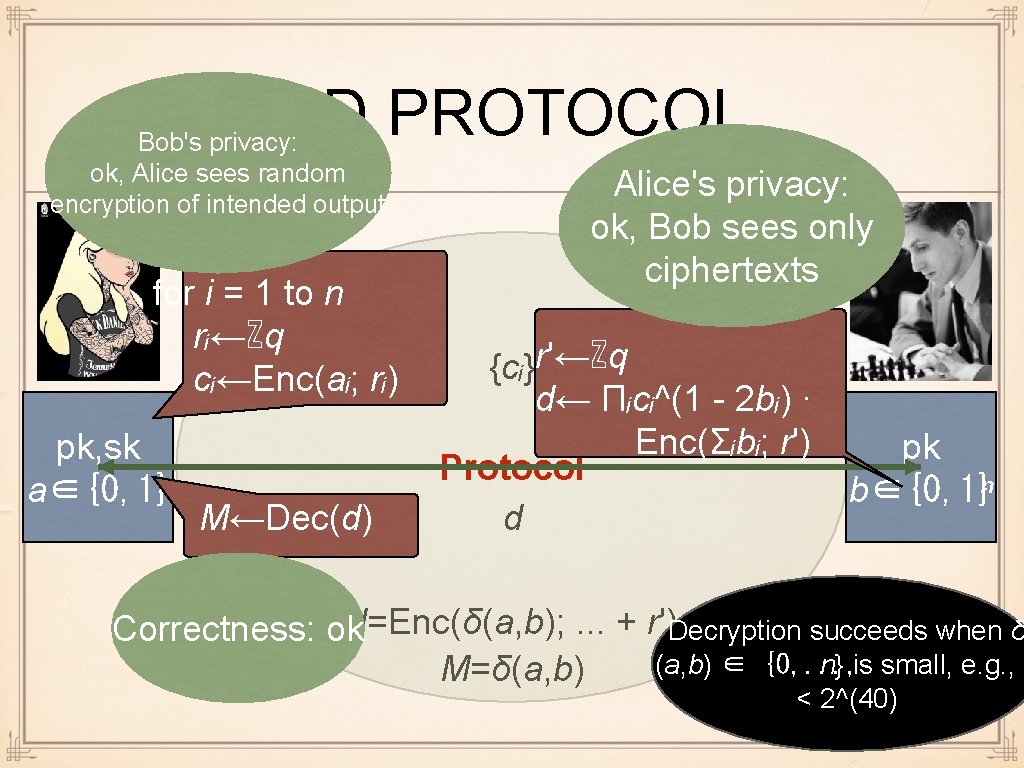
HD PROTOCOL Bob's privacy: ok, Alice sees random encryption of intended output for i = 1 to n rᵢ←ℤq cᵢ←Enc(aᵢ; rᵢ) pk, sk a∈{0, 1}ⁿ M←Dec(d) Alice's privacy: ok, Bob sees only ciphertexts {cᵢ}r'←ℤq d← Πᵢcᵢ^(1 - 2 bᵢ) · Enc(Σᵢbᵢ; r') pk Protocol b∈{0, 1}ⁿ d Correctness: okd=Enc(δ(a, b); . . . + r')Decryption succeeds when δ (a, b) ∈ {0, . . . , n} is small, e. g. , n M=δ(a, b) < 2^(40)

REAL PROTOCOL: CPIR Assume any privacy-preserving database application Most trivial operation: Alice queries one element from Bob's database subprotocol in myriad other protocols How to do it so that Bob has no clue which element was obtained? simplest case: Bob's database has two elements

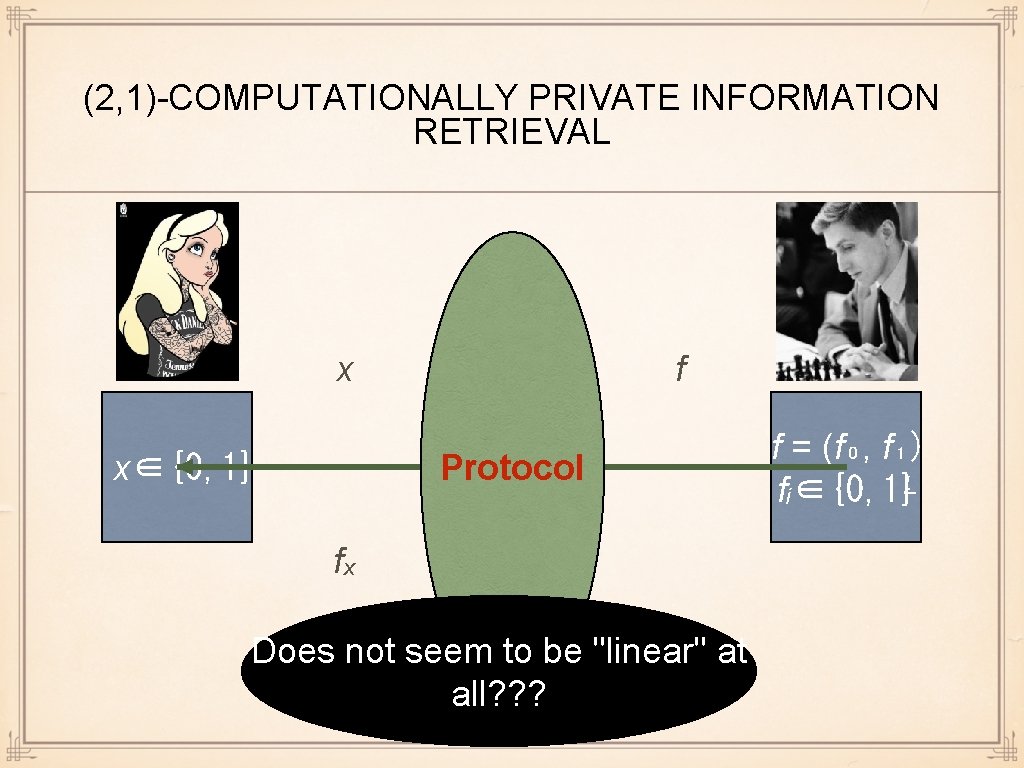
(2, 1)-COMPUTATIONALLY PRIVATE INFORMATION RETRIEVAL x TTP f Protocol x∈{0, 1} fₓ Does not seem to be "linear" at all? ? ? f = (f₀, f₁) fᵢ∈{0, 1}ᴸ

QUIZ: CPIR PROTOCOL Note x∈{0, 1} Moreover, Bob knows f₀ and f₁ fₓ = f₀ ·[x = 0] + f₁ ·[x = 1] fₓ = f₀ · (1 x)- + f₁ x = f₀ + f(₁ "linear" and thus we can -f₀) x construct 2 MAH for (2, 1)CPIR

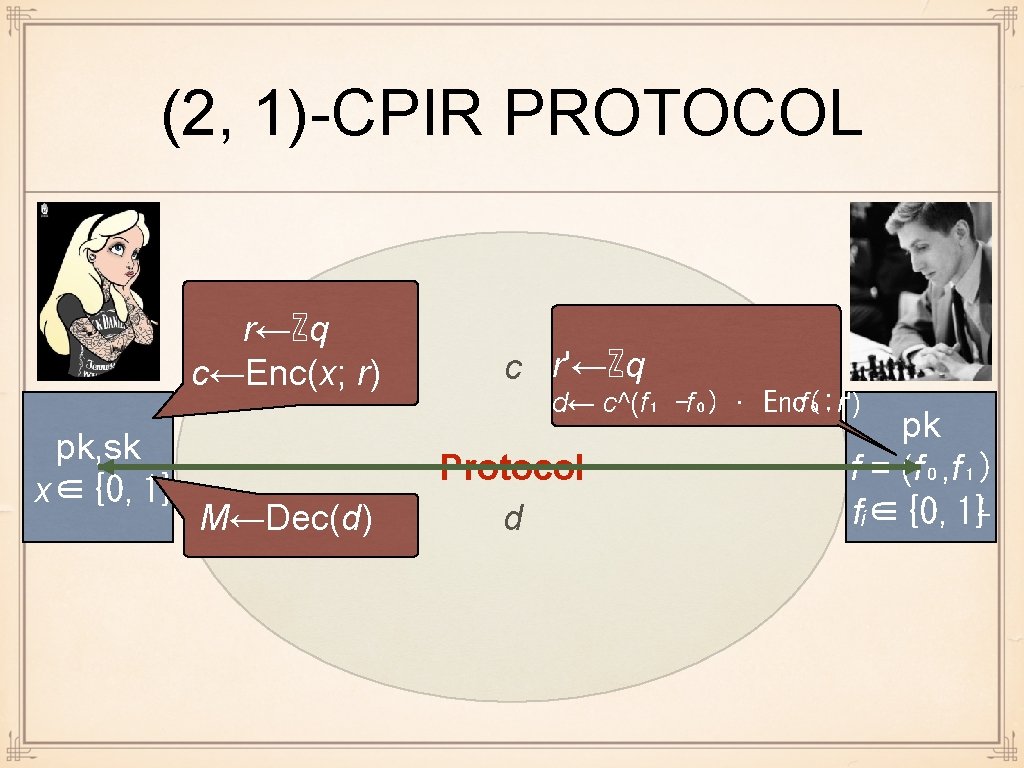
(2, 1)-CPIR PROTOCOL r←ℤq c←Enc(x; r) pk, sk x∈{0, 1} M←Dec(d) c r'←ℤq d← c^(f₁ -f₀) · Enc( f₀; r') Protocol d pk f = (f₀, f₁) fᵢ∈{0, 1}ᴸ

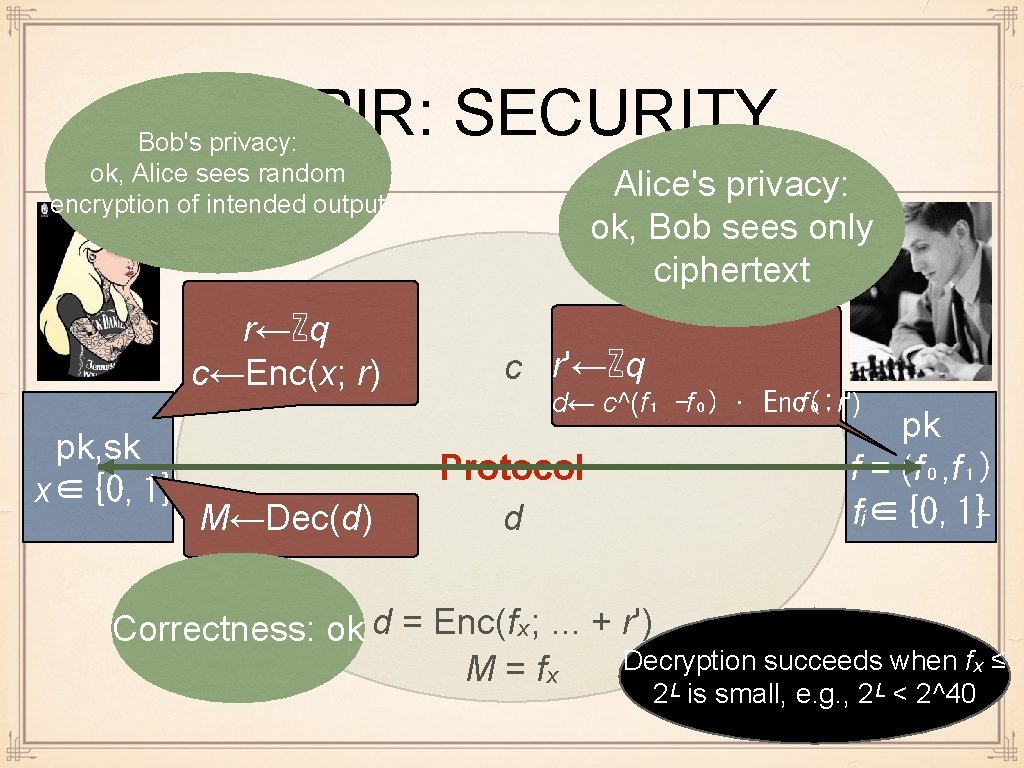
CPIR: SECURITY Bob's privacy: ok, Alice sees random encryption of intended output r←ℤq c←Enc(x; r) pk, sk x∈{0, 1} M←Dec(d) Alice's privacy: ok, Bob sees only ciphertext c r'←ℤq d← c^(f₁ -f₀) · Enc( f₀; r') Protocol d pk f = (f₀, f₁) fᵢ∈{0, 1}ᴸ Correctness: ok d = Enc(fₓ; . . . + r') Decryption succeeds when fₓ ≤ M = fₓ 2ᴸ is small, e. g. , 2ᴸ < 2^40

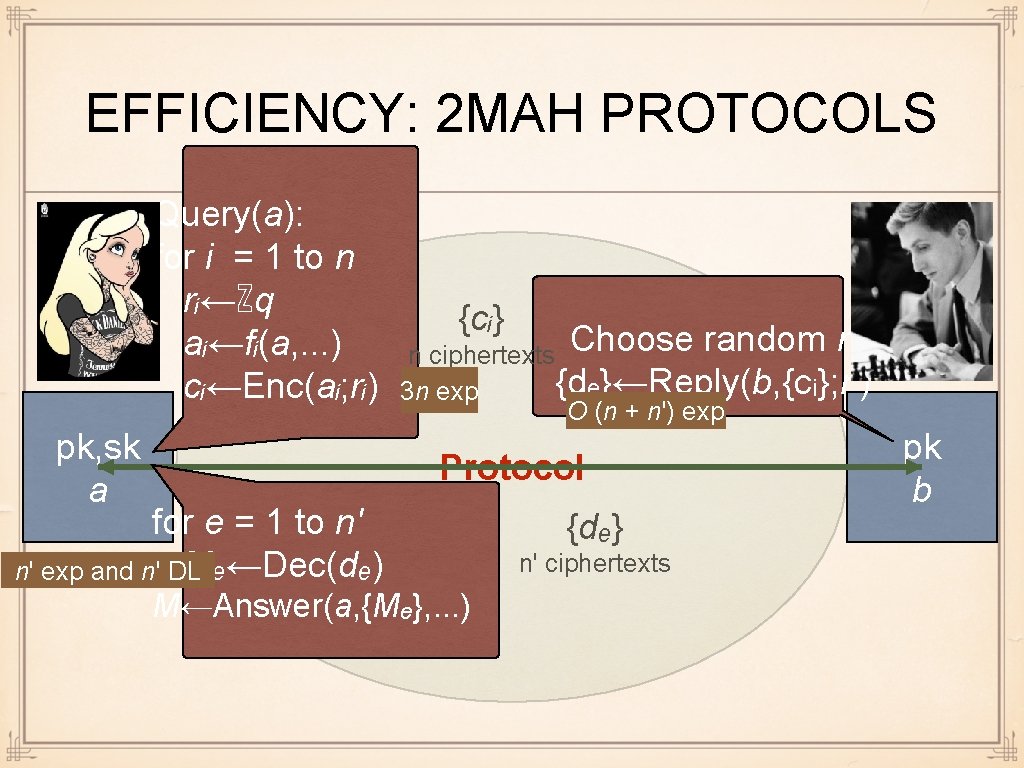
EFFICIENCY: 2 MAH PROTOCOLS Query(a): for i = 1 to n rᵢ←ℤq aᵢ←fᵢ(a, . . . ) cᵢ←Enc(aᵢ; rᵢ) pk, sk a {cᵢ} Choose random r' n ciphertexts {dₑ}←Reply(b, {cᵢ}; r') 3 n exp O (n + n') exp Protocol for e = 1 to n' Mₑ←Dec(dₑ) n' exp and n' DL M←Answer(a, {Mₑ}, . . . ) {dₑ} n' ciphertexts pk b

ON EFFICIENCY Alice: n encryptions + n' decryptions that is, (3 n + Θ(n')) exponentiations + n' DL-s Since exponentiation Bob: takes Θ(L^2. 58) bit-ops by using Karatsuba depends very much on protocol multiplication, and DL takes Θ(2^(L/2)) bit-ops, Usually Θ(n + n') exponentiations for large L, DL is the bottleneck

"BITWISE" TRICKS DL timing: Θ(n' 2^(L / 2)) bit-ops /* linear in n' but exponential in L */ Common trick: let Alice encrypt every bit separately, and then construct protocol so that every final ciphertext also encrypts a bit Θ (L) times more DL-s, but each DL gets "1 -bit" input DL-s dominated by Θ (n'L) bit-ops Drawback: comm. and Bob's comp. increased by factor of Θ (L)

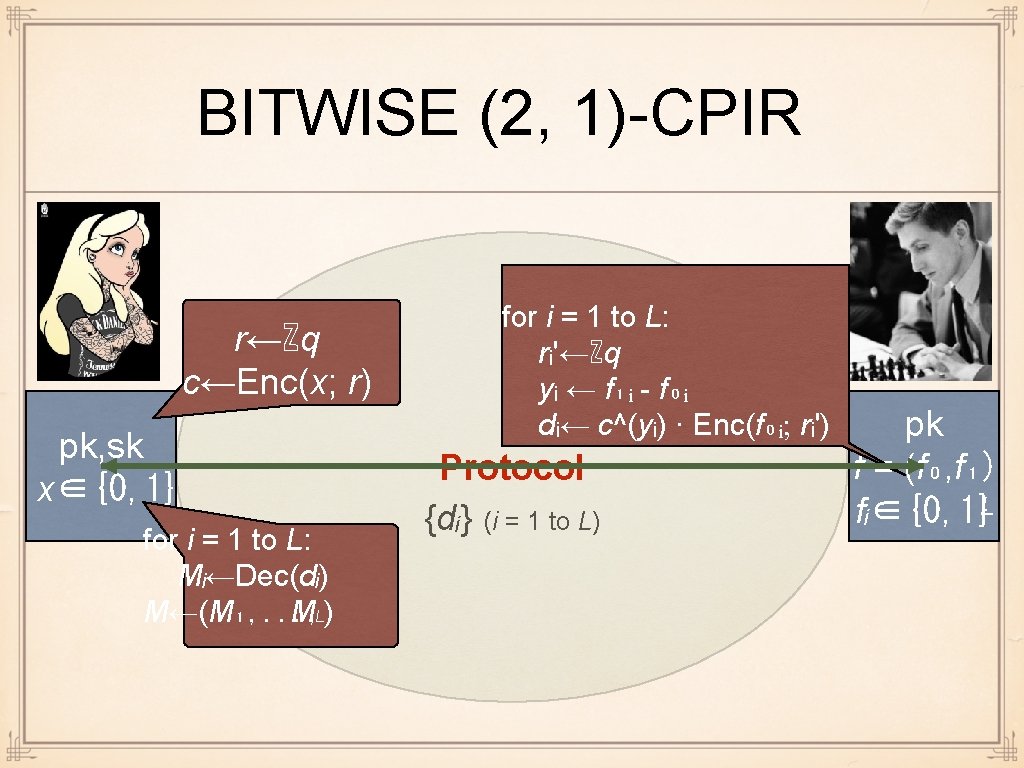
BITWISE (2, 1)-CPIR r←ℤq c←Enc(x; r) pk, sk x∈{0, 1} for i = 1 to L: Mᵢ←Dec(dᵢ) M←(M₁, . . . , ML ) for i = 1 to L: rᵢ'←ℤq c yᵢ ← f₁ᵢ - f₀ᵢ dᵢ← c^(yᵢ) · Enc(f₀ᵢ; rᵢ') Protocol {dᵢ} (i = 1 to L) pk f = (f₀, f₁) fᵢ∈{0, 1}ᴸ

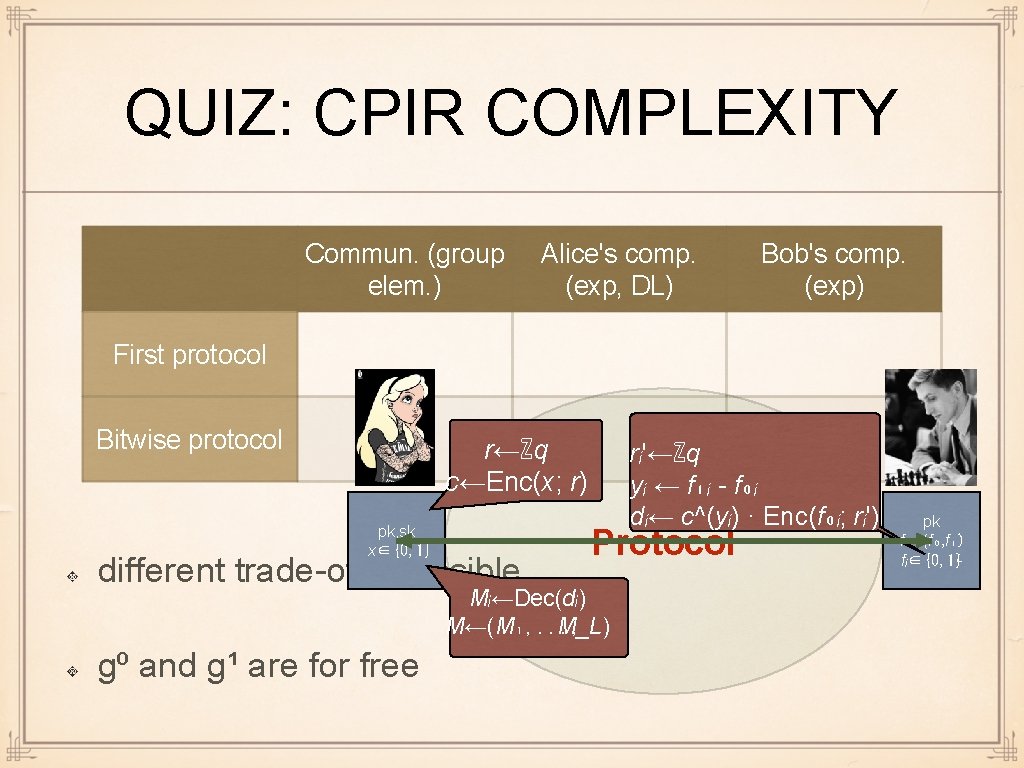
QUIZ: CPIR COMPLEXITY Commun. (group elem. ) Alice's comp. (exp, DL) Bob's comp. (exp) First protocol Bitwise protocol r←ℤq c←Enc(x; r) pk, sk x∈{0, 1} different trade-offs possible Protocol Mᵢ←Dec(dᵢ) M←(M₁, . . . , M_L) g⁰ and g¹ are for free rᵢ'←ℤq yᵢ ← f₁ᵢ - f₀ᵢ dᵢ← c^(yᵢ) · Enc(f₀ᵢ; rᵢ') pk f = (f₀, f₁) fᵢ∈{0, 1}ᴸ

QUIZ: CPIR COMPLEXITY First protocol Bitwise protocol Commun. (group elem. ) Alice's comp. (exp, DL) Bob's comp. (exp) 4 3 exp + DL(L) 5 2 L + 2 (L + 2) exp + L·DL(1) 2 L different trade-offs possible r←ℤq rᵢ'←ℤq c←(g^x hʳ, gʳ) yᵢ ← f₁ᵢ - f₀ᵢ pk, sk x∈{0, 1} g⁰ and g¹ are for free dᵢ← (c 1, c 2)^(yᵢ) · (g^(f₀ᵢ)h^(rᵢ'), g^(rᵢ')) Protocol Mᵢ← dlog (dᵢ₁ / d�₂ ^sk) M←(M₁, . . . , M_L) pk f = (f₀, f₁) fᵢ∈{0, 1}ᴸ

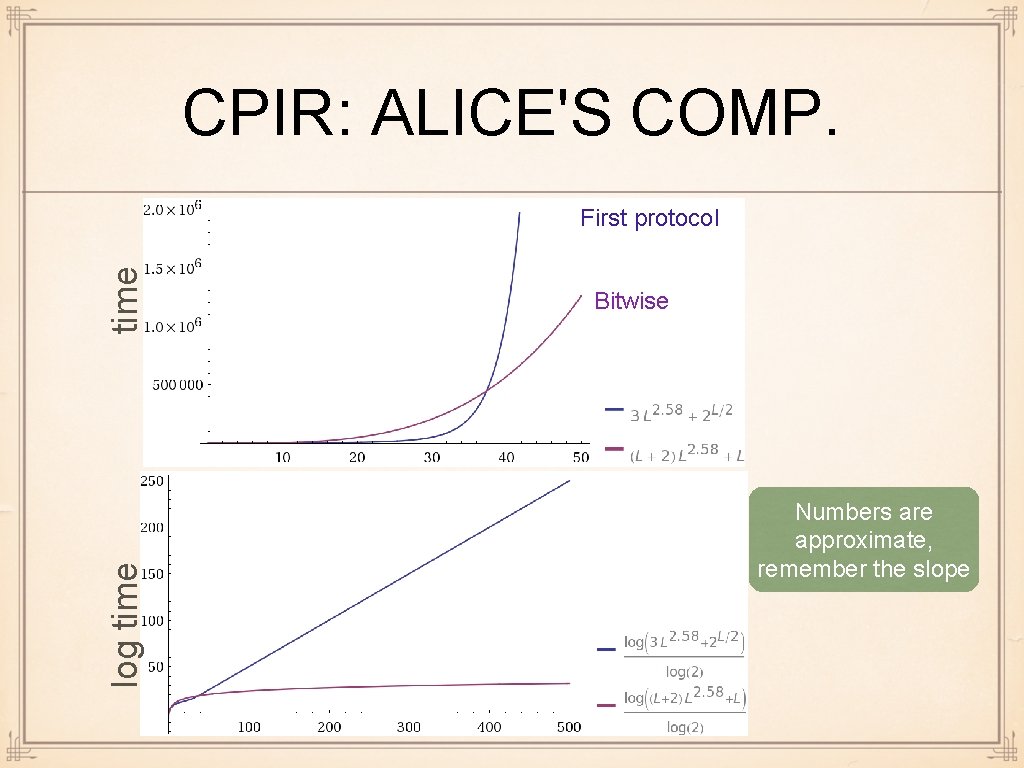
CPIR: ALICE'S COMP. log time First protocol Bitwise Numbers are approximate, remember the slope

REMARKS Bitwise execution: logical and (more) efficient solution for CPIR In other protocols, not so easy Millionaire: output bit depends on all input bits Lifted Elgamal-based millionaire protocol with >40 dimensional vectors is way too slow Need other solutions

ON ART OF PROTOCOL DESIGN Figure out how much resources you have Communication, Alice's and Bob's computation Design a protocol that achieves a good tradeoff Also: efficiency vs assumption

ABOUT SECURITY Currently: semihonest model Alice and Bob follow protocol but "eavesdrop" Malicious model Later lectures Given protocol secure in semihonest model, add zero knowledge proofs

ABOUT SECURITY The protocols are "designed" to be secure Correctness (semihonest model) Follows from protocol design Alice's privacy (semihonest model) Bob only sees some random encryptions, thus follows from IND-CPA security of used cryptosystem Bob's privacy (semihonest model) Alice only sees random encryptions of intended output(s)

MORE ON SECURITY Alice's privacy: Defined like IND-CPA for public-key encryption Bob cannot distinguish between Alice's messages corresponding to Alice's any two inputs a₀ and a₁ Bob's privacy: some computational assumption no computational assumptions Alice should obtain no information about Bob's input b, except what is obvious from her input a and correct output fₐ(a, b)

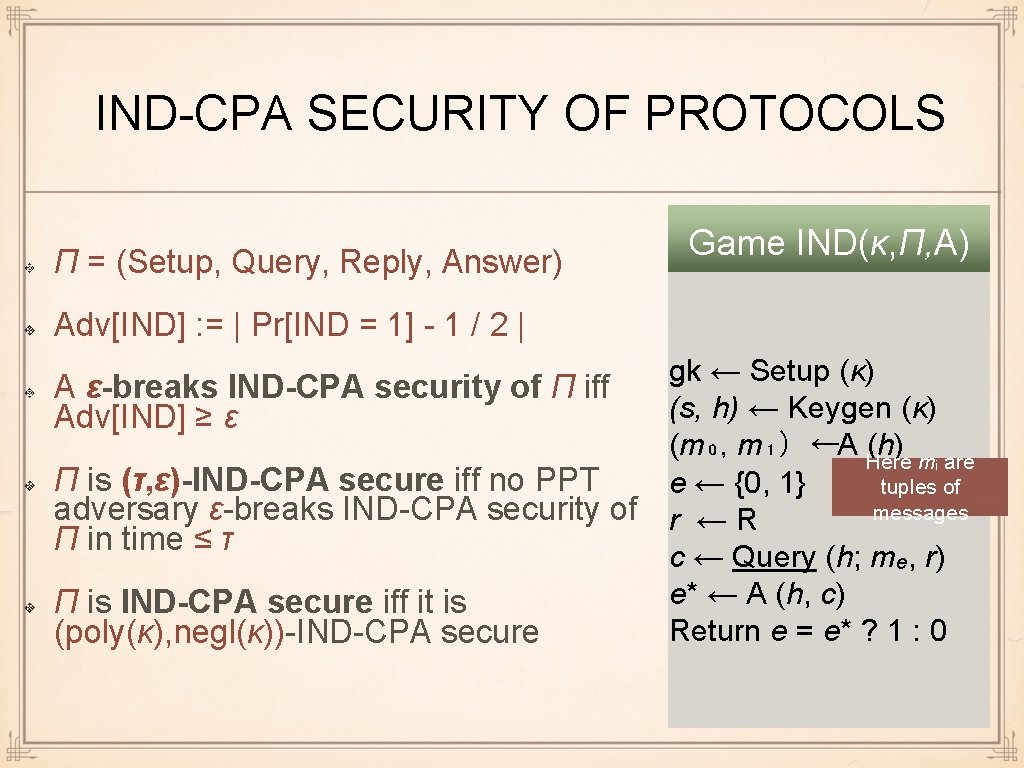
IND-CPA SECURITY OF PROTOCOLS Π = (Setup, Query, Reply, Answer) Game IND(κ, Π, A) Adv[IND] : = | Pr[IND = 1] - 1 / 2 | A ε-breaks IND-CPA security of Π iff Adv[IND] ≥ ε Π is (τ, ε)-IND-CPA secure iff no PPT adversary ε-breaks IND-CPA security of Π in time ≤ τ Π is IND-CPA secure iff it is (poly(κ), negl(κ))-IND-CPA secure gk ← Setup (κ) (s, h) ← Keygen (κ) (m₀, m₁) ←A Here (h) mᵢ are e ← {0, 1} tuples of messages r ←R c ← Query (h; mₑ, r) e* ← A (h, c) Return e = e* ? 1 : 0

IND-CPA SECURITY PROOFS IND-CPA security proofs of all 2 MAH protocols are tautologies Since Elgamal is IND-CPA secure, and Bob only sees random ciphertexts, the protocol is IND-CPA secure

BOB'S PRIVACY PROOFS Also tautology if the protocol is well constructed Alice only sees random encryption of the intended output Thus even if Alice is omnipotent, Alice can only recover intented output

STUDY OUTCOMES Functionality vs protocol 2 MAH protocols, examples Different efficiency aspects DL dominates when outputs get longer. . . Tricks (some of them!): linearization, bitwise Security of 2 MAH protocols

NEXT LECTURE How to construct protocols with large outputs without "bitwising" Trapdoor discrete logarithm Paillier cryptosystem