CRYPTOGRAPHIC PROTOCOLS 2015 LECTURE 11 Sigma protocols Helger

CRYPTOGRAPHIC PROTOCOLS 2015, LECTURE 11 Sigma protocols Helger Lipmaa University of Tartu, Estonia

UP TO NOW Introduction to the field Secure computation protocols Can do almost everything in semihonest model Introduction to malicious model

THIS TIME Reminder: zero knowledge and malicious model Σ-Protocols: a particular kind of "ZK" protocols motivation security definitions examples

REMINDER: GENERAL PROTOCOL DESIGN Design a passively secure protocol I. e. , that protects privacy given participants follow the protocol. . . take any protocol we have seen up to now Make it secure in the malicious model by of course this needs "some" care: adding ZK proofs to all messages you need to know which ZK to add efficiency, . . .

PROOFS VS PROOFS OF KNOWLEDGE ZK Proof: Complete: honest prover convinces honest verifier Sound: dishonest prover does not convince honest verifier Zero Knowledge: dishonest verifier only gets to know that honest prover is honest ZK Proof of Knowledge: (in addition) Proof of Knowledge (stronger soundness): honest prover convinces honest verifier that he knows "why he is honest" --- i. e. , knows some secret "witness"

REMINDER: AUTHENTICATION Prover P Verifier V pk, sk pk I am The Doctor Prove it! sk ZK proof of knowledge of sk Proof: I can sign your document with Doctor's secret key. Leaks information (new signatures), not really ZK. ZK proofs do not make sense in this application Proof of knowledge: I know sk (nothing else is leaked)

MOTIVATION BY EXAMPLES We first describe a very simple protocol that intuitively is a "secure" ZK proof of knowledge We will later see other protocols that are "secure" in the same sense Common name: Σ-protocols We then formally define security of such protocols

GRAPH ISOMORPHISM Two graphs G₁ = V ( ₁, E₁) and G₂ = V ( ₂, E₂) are isomorphic if there exists a map φ: V₁ → V₂ such that 1. φ is bijection 2. (v₁, v₂) ∈E₁ iff (φ(v₁), φ(v₂)) ∈E₂ Intuitively: isomorphism We write then G₂ = φ (G₁) is a consistent renaming of vertices, together with Best known algorithm for GI [Babai, 2015]: edges between them time 2^((log n)^(O (1))) --- thus hard problem (not poly-time) Like factoring, not known to be in P or NP-complete Better classical algorithm but no known efficient quantum algorithm

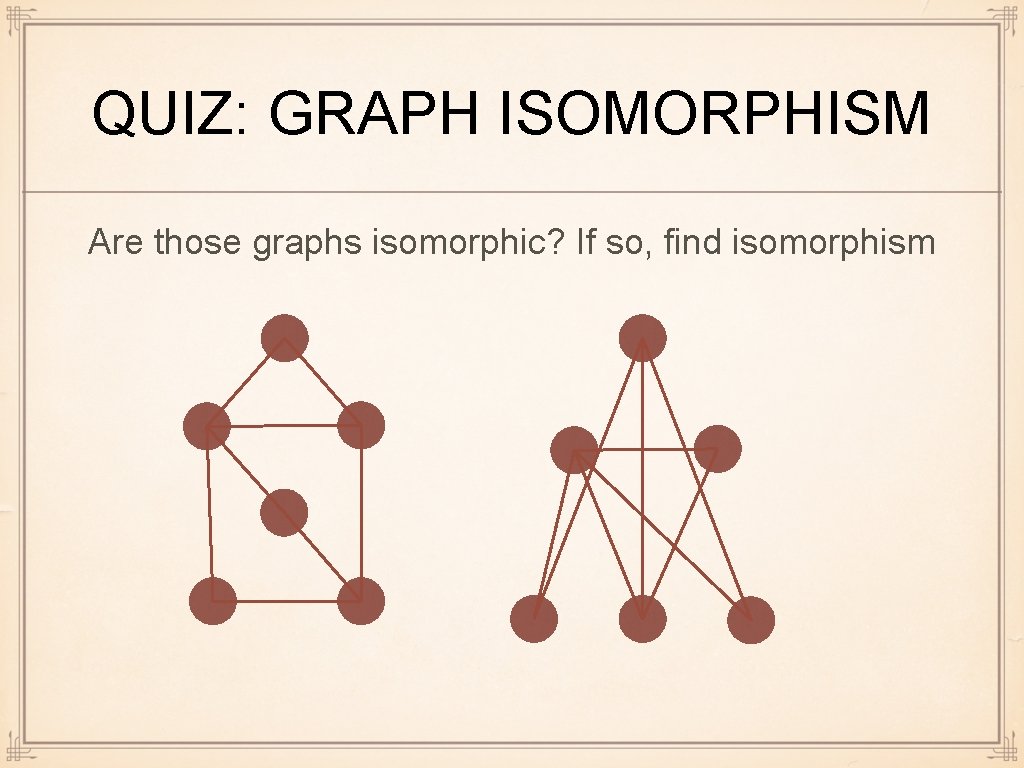
QUIZ: GRAPH ISOMORPHISM Are those graphs isomorphic? If so, find isomorphism

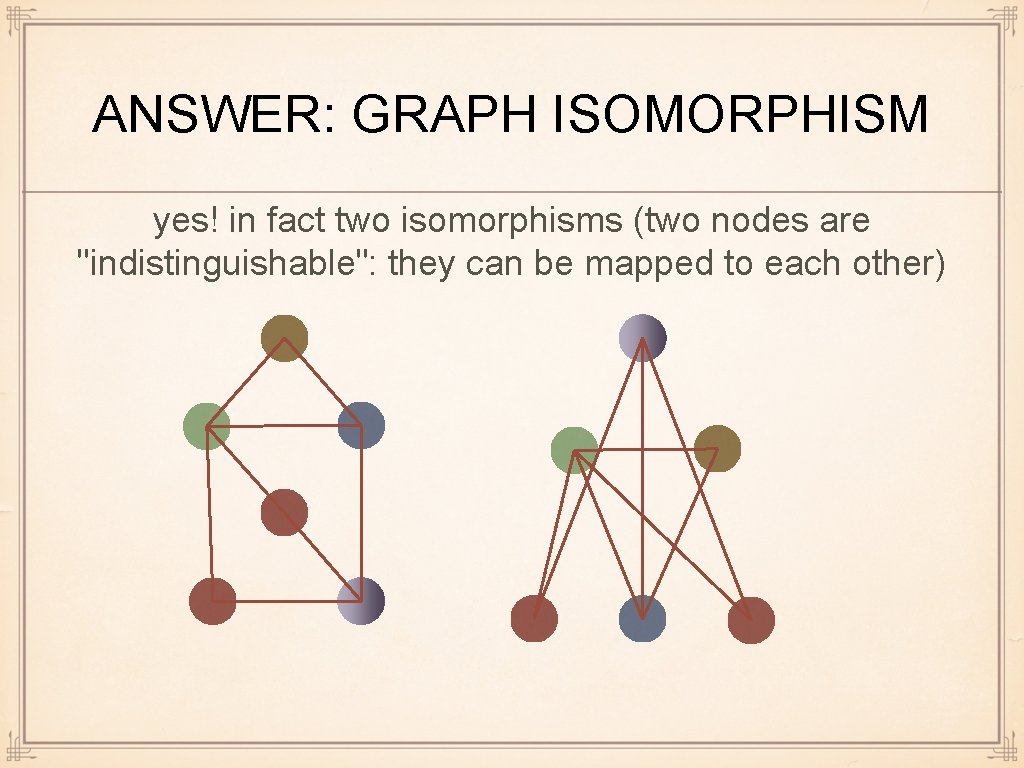
ANSWER: GRAPH ISOMORPHISM yes! in fact two isomorphisms (two nodes are "indistinguishable": they can be mapped to each other)

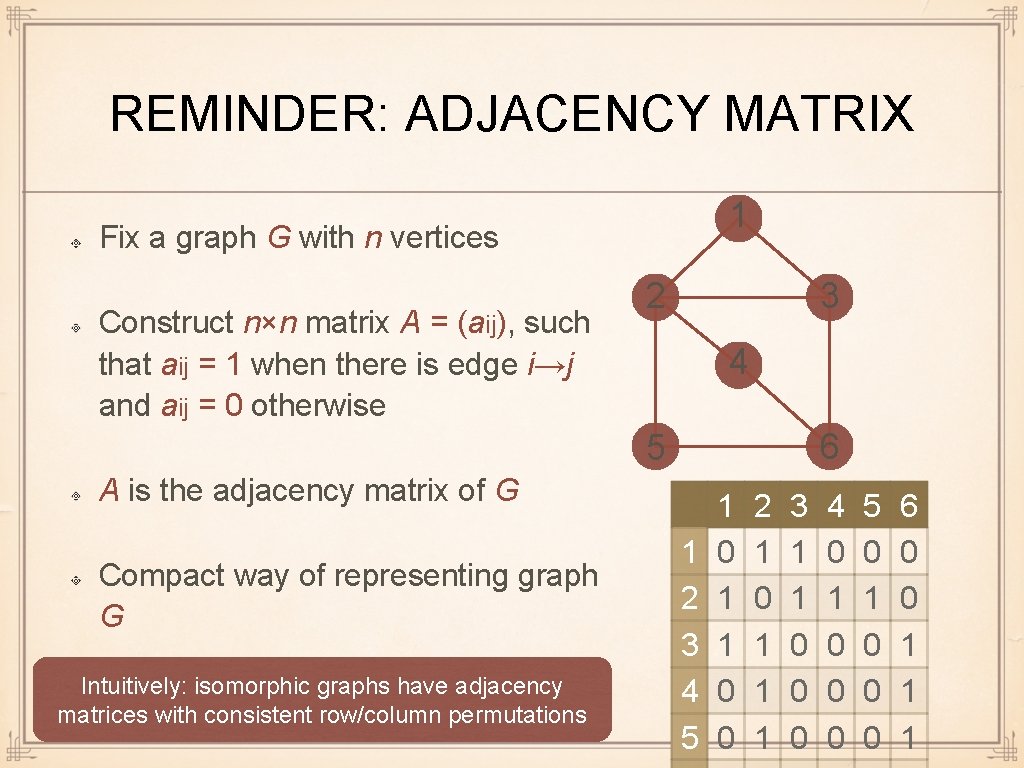
REMINDER: ADJACENCY MATRIX 1 Fix a graph G with n vertices Construct n×n matrix A = (aij), such that aij = 1 when there is edge i→j and aij = 0 otherwise 2 3 4 6 5 A is the adjacency matrix of G Compact way of representing graph G Intuitively: isomorphic graphs have adjacency matrices with consistent row/column permutations 1 2 3 4 5 1 0 1 1 0 0 2 1 0 1 1 1 3 1 1 0 0 0 4 0 1 0 0 0 5 0 1 0 0 0 6 0 0 1 1 1

QUIZ: Σ-PROTOCOL FOR GI QUIZ: can you think of any kind of protocol that convinces verifier that G₁ prover knows isomorphism, without revealing it? : -) G₂

QUIZ: Σ-PROTOCOL FOR GI QUIZ: can you think of any kind of protocol that convinces verifier that G₁ prover knows isomorphism, withoutprob. 1/2 revealing it? : -) G₂ prob. 1/2 H Hint: let prover to prove that for a third graph he knows that this is isomorphic to either of these two graphs

ANSWER: Σ-PROTOCOL FOR GI Prover creates a random isomorphic copy H of G₁ Verifier asks Prover to reveal, for random c, the isomorphism between H and Gc Clearly, honest Prover succeeds always If G₁ and G₂ are not isomorphic, Prover fails with probability 1/2 Random isomorphic copy of G with adj. matrix A: a graph whose adjacency matrix is a random row/column permutation of A

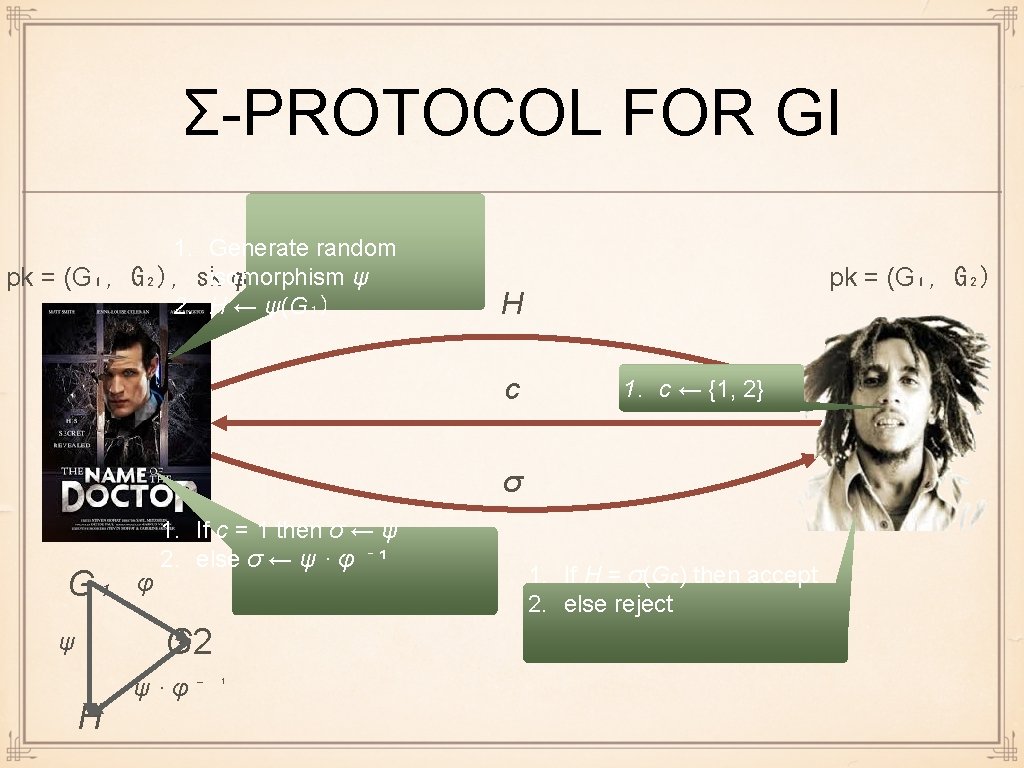
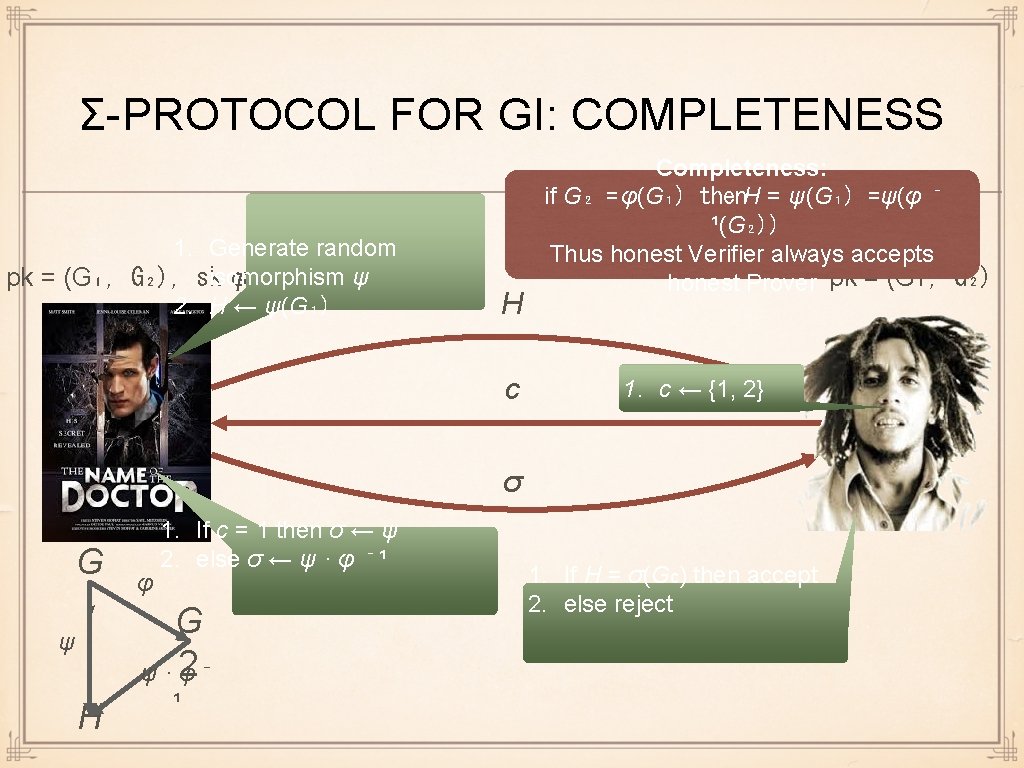
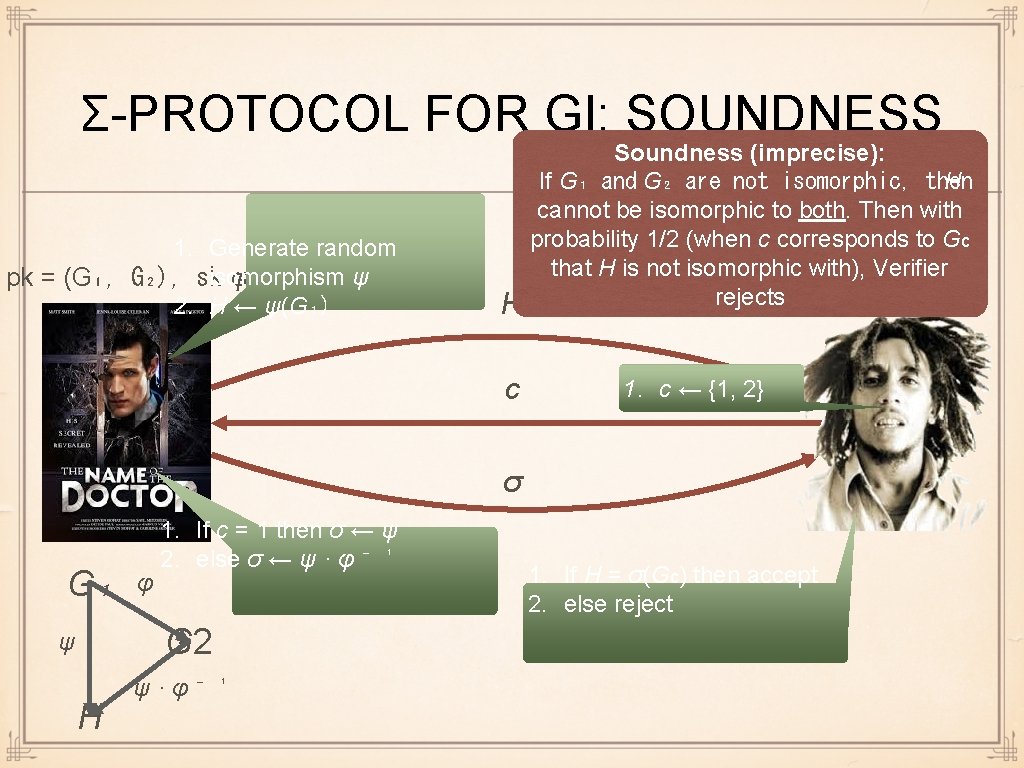
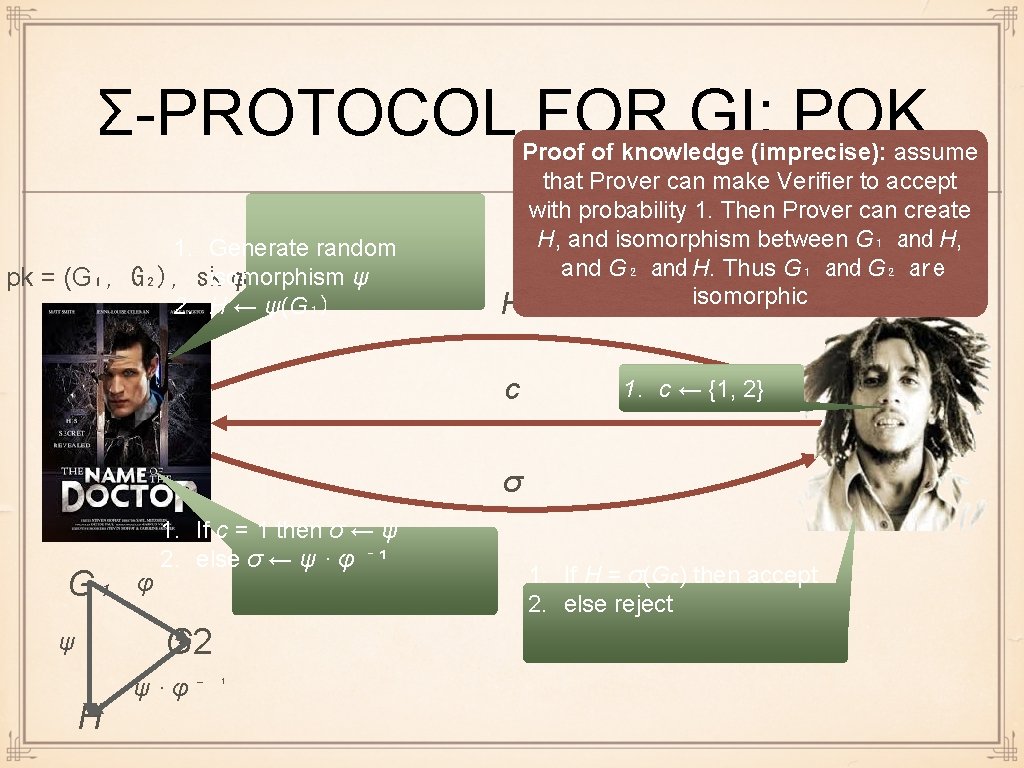
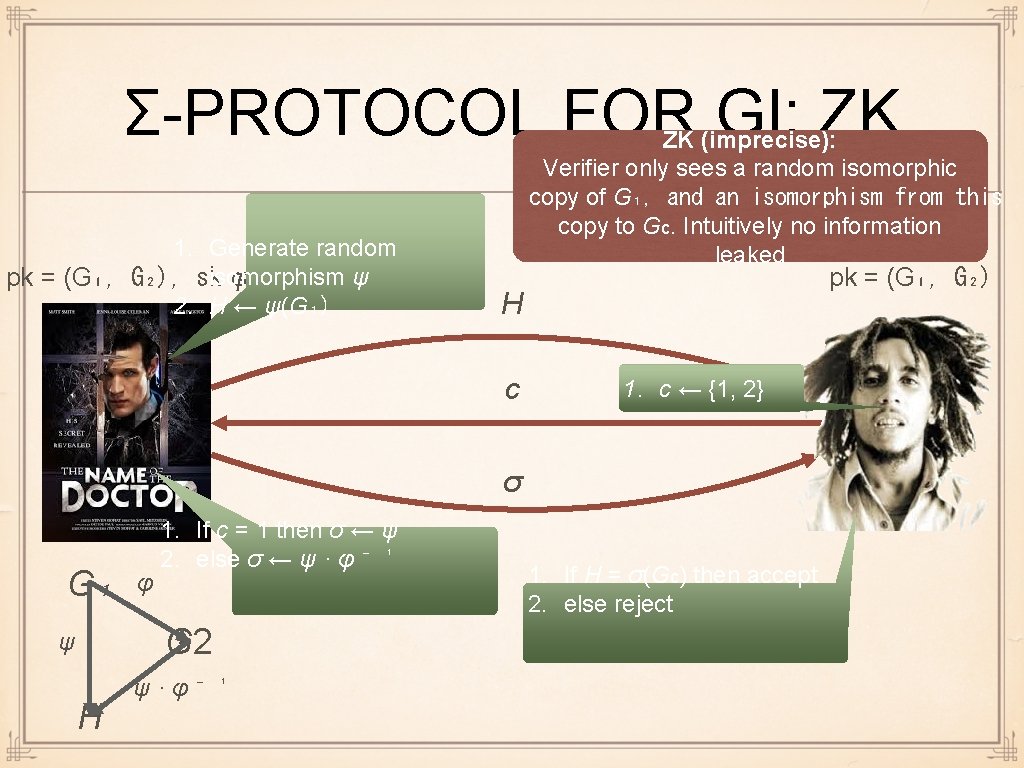
Σ-PROTOCOL FOR GI 1. Generate random ψ pk = (G₁, G₂), skisomorphism φ = 2. H ← ψ(G₁) pk = (G₁, G₂) H c 1. c ← {1, 2} σ G₁ φ 1. If c = 1 then σ ← ψ 2. else σ ← ψ · φ ⁻ ¹ G 2 ψ H ψ·φ⁻ ¹ 1. If H = σ(Gc) then accept 2. else reject

Σ-PROTOCOL FOR GI: COMPLETENESS 1. Generate random ψ pk = (G₁, G₂), skisomorphism φ = 2. H ← ψ(G₁) H c Completeness: if G₂ = φ(G₁) then. H = ψ(G₁) =ψ(φ ⁻ ¹(G₂)) Thus honest Verifier always accepts honest Prover pk = (G₁, G₂) 1. c ← {1, 2} σ G ₁ ψ H φ 1. If c = 1 then σ ← ψ 2. else σ ← ψ · φ ⁻ ¹ G 2⁻ ψ·φ ¹ 1. If H = σ(Gc) then accept 2. else reject

Σ-PROTOCOL FOR GI: SOUNDNESS 1. Generate random ψ pk = (G₁, G₂), skisomorphism φ = 2. H ← ψ(G₁) H c Soundness (imprecise): If G₁ and G₂ are not isomorphic, then H cannot be isomorphic to both. Then with probability 1/2 (when c corresponds to Gc that H is not isomorphic with), pk =Verifier (G₁, G₂) rejects 1. c ← {1, 2} σ G₁ φ 1. If c = 1 then σ ← ψ 2. else σ ← ψ · φ ⁻ ¹ G 2 ψ H ψ·φ⁻ ¹ 1. If H = σ(Gc) then accept 2. else reject

Σ-PROTOCOL FOR GI: POK 1. Generate random ψ pk = (G₁, G₂), skisomorphism φ = 2. H ← ψ(G₁) Proof of knowledge (imprecise): assume that Prover can make Verifier to accept with probability 1. Then Prover can create H, and isomorphism between G₁ and H, and G₂ and H. Thus G₁ and are G₂) pk =G₂(G₁, isomorphic H c 1. c ← {1, 2} σ G₁ φ 1. If c = 1 then σ ← ψ 2. else σ ← ψ · φ ⁻ ¹ G 2 ψ H ψ·φ⁻ ¹ 1. If H = σ(Gc) then accept 2. else reject

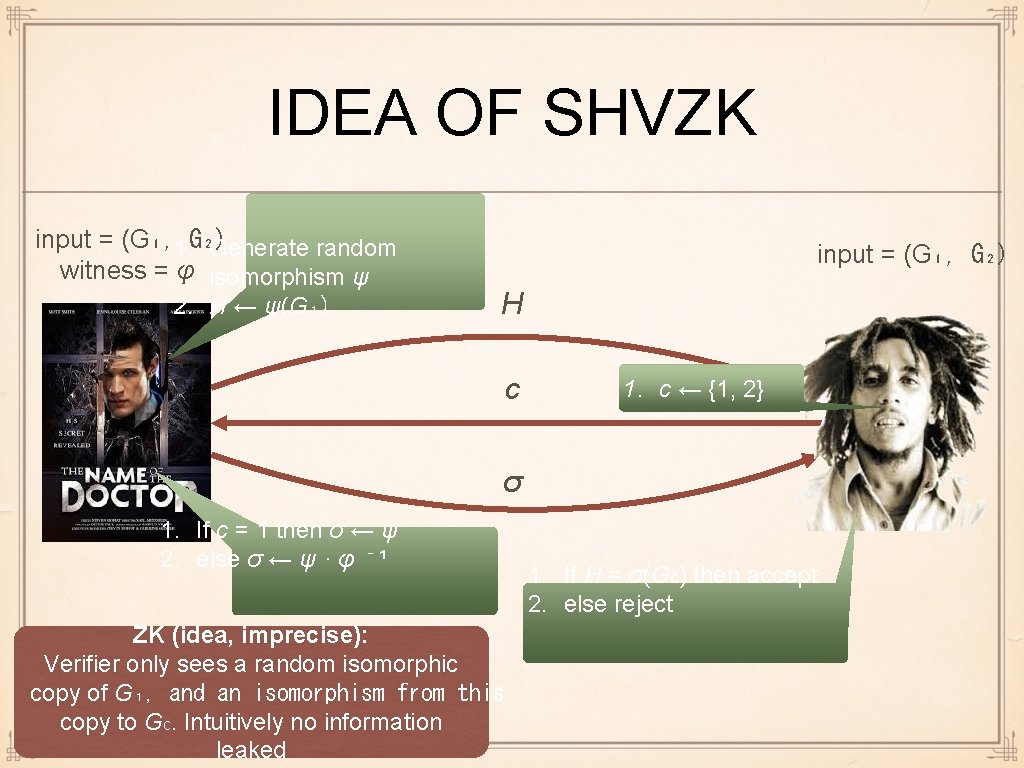
Σ-PROTOCOL FOR GI: ZK 1. Generate random ψ pk = (G₁, G₂), skisomorphism φ = 2. H ← ψ(G₁) ZK (imprecise): Verifier only sees a random isomorphic copy of G₁, and an isomorphism from this copy to Gc. Intuitively no information leaked pk = (G₁, G₂) H c 1. c ← {1, 2} σ G₁ φ 1. If c = 1 then σ ← ψ 2. else σ ← ψ · φ ⁻ ¹ G 2 ψ H ψ·φ⁻ ¹ 1. If H = σ(Gc) then accept 2. else reject

KNOWLEDGE ERROR Honest Prover accepted with probability 1 Dishonest Prover accepted with non-zero probability κ = 1/2 Def (informal). Κnowledge error = κ Every Σ-protocol has non-zero knowledge error Prover can just guess Verifier's challenge and prepare first message accordingly

A BIT OF TERMINOLOGY All such proofs are of type: does input x belong to language L? The prover knows a witness w Proving x∈L can be done efficiently, given w Proof of knowledge: Prover proves he knows w GI: L = {(G₁, G₂): ∃ φ: G₂ = φ(G₁)} x = (G₁, G₂) w=φ

Σ-PROTOCOLS: SYNTAX input, witness 1 st message: commitment a input 2 nd message: challenge c 3 rd message: response z Requirement: c is chosen from some challenge set C randomly. (Does not depend on a!) Terminology: public coin protocol

Σ-PROTOCOLS: FORMAL DEFINITION Definition A protocol (P, V) is a Σ-protocol, if 1. it is a three-message public-coin protocol: it has three messages, with the prover starting, and the second message is completely random and independent of the first message 2. Security: it is complete, specially sound, and special honest-verifier zero knowledge

Σ-PROTOCOLS: SECURITY input, witness 1 st message: commitment a input 2 nd message: challenge c 3 rd message: response z 1. Completeness 2. Special Soundness 3. Special Honest-Verifier ZK (SHVZK)

Σ-PROTOCOLS: SECURITY input, witness 1 st message: commitment a input 2 nd message: challenge c 3 rd message: response z Completeness: if Prover is honest then honest Verifier always accepts. GI protocol has it

Σ-PROTOCOLS: SECURITY input, witness 1 st message: commitment a input 2 nd message: challenge c 3 rd message: response z Special Soundness (with knowledge error κ): if Prover is dishonest then honest Verifier accepts with probability not much larger than κ. GI protocol has it (intuitively)

SPECIAL SOUNDNESS: MORE Our proof of special soundness for GI relied on the next (informal) fact: If (possibly malicious) P* makes honest V always accept, then P* knows isomorphism between both H and G₁, and between H and G₂ We will next make this intuition more formal

SEMIFORMALLY: SPECIAL SOUNDNESS Assume a dishonest prover P* can make honest verifier V to accept with some probability ε > κ This guarantees κ is really the "limit" Then V can "extract" the witness (here, φ) from P* in time, related to ε - κ => we have a proof of knowledge However, V is a pre-defined algorithm We need to define a new algorithm, an extractor K, that communicates with P* and extracts φ from P* As in reductions, K can only communicate with P*. K does not know anything else about P* apart from what P* outputs

FORMALLY: SPECIAL SOUNDNESS Definition A Σ-protocol (P, V) is specially sound, if there exists a probabilistic expected poly-time extractor algorithm K, such that if a prover P* (possibly malicious) can make V to accept with a probability ε > κ, then K can --- after playing the role of V in possibly many instances of the protocol with P --output the value of the witness However, K must have some "superpower": otherwise V could do the same and extract witness. Here: rewinding

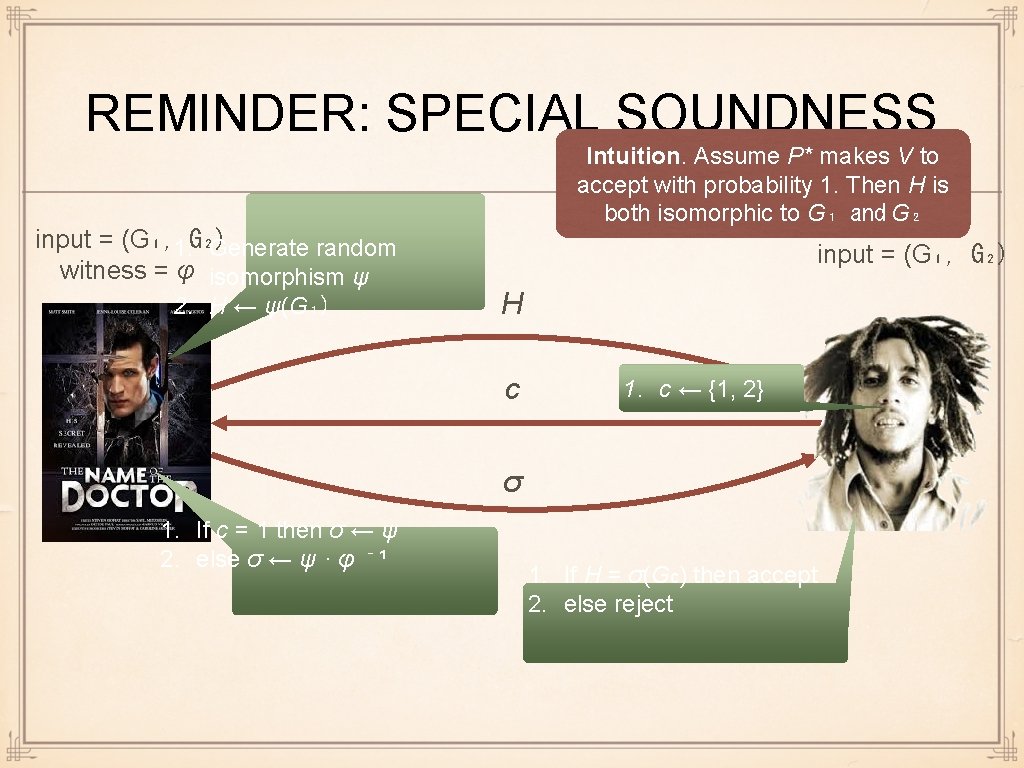
REMINDER: SPECIAL SOUNDNESS input = (G₁, 1. G₂) Generate random witness = φ isomorphism ψ 2. H ← ψ(G₁) Intuition. Assume P* makes V to accept with probability 1. Then H is both isomorphic to G₁ and G₂ input = (G₁, G₂) H c 1. c ← {1, 2} σ 1. If c = 1 then σ ← ψ 2. else σ ← ψ · φ ⁻ ¹ 1. If H = σ(Gc) then accept 2. else reject

SPECIAL SOUNDNESS: REWINDING input = (G₁, G₂) witness = φ input = (G₁, G₂) H c σ Formally, K plays V in the protocol. K does the following: Execute the protocol once with c = 1. Store (H, c, σ) Create a breakpoint for prover directly after sending H

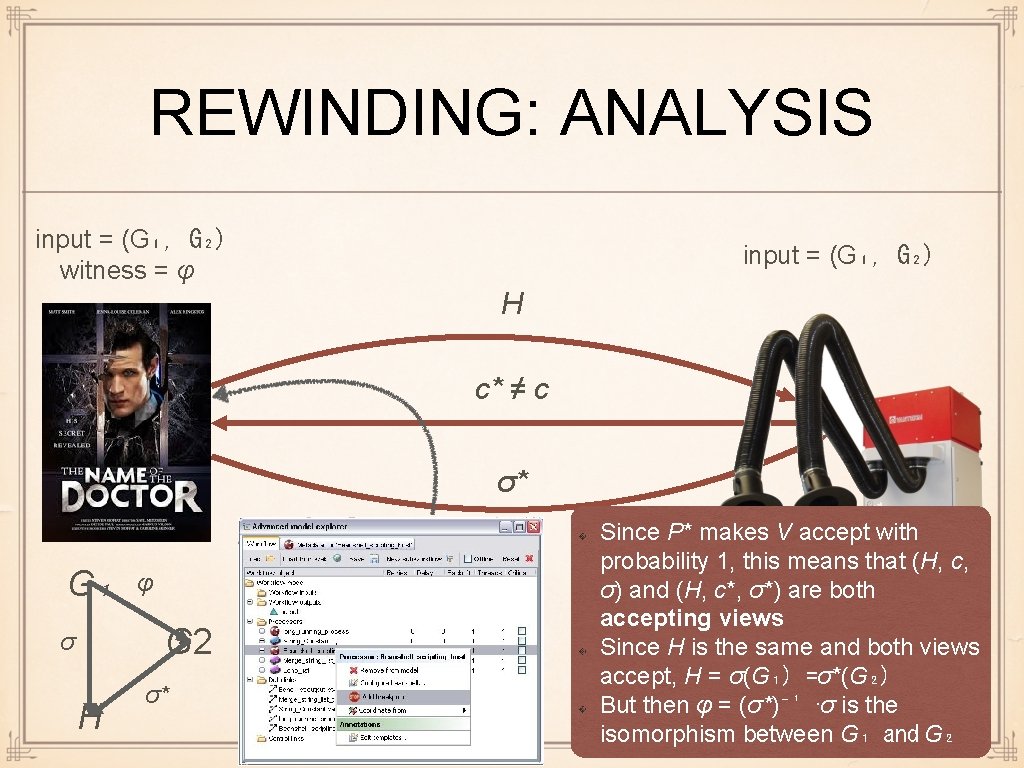
SPECIAL SOUNDNESS: REWINDING input = (G₁, G₂) witness = φ input = (G₁, G₂) H c* ≠ c σ* After that: Rewind P* to the breakpoint (the state P* was directly after sending H). Challenge with c* = 2, get P*'s answer, and store (H, c*, σ*)

REWINDING: ANALYSIS input = (G₁, G₂) witness = φ input = (G₁, G₂) H c* ≠ c σ* G₁ φ G 2 σ H σ* Since P* makes V accept with probability 1, this means that (H, c, σ) and (H, c*, σ*) are both accepting views Since H is the same and both views accept, H = σ(G₁) =σ*(G₂) But then φ = (σ*)⁻¹ ·σ is the isomorphism between G₁ and G₂

GENERAL K Assume P* makes V to accept with prob. ε >κ Probability ε is both over the randomness ω of P* and c of V Construct a Boolean matrix A P* (x, ω) generates a, P* (x, ω, c) generates z A[ω, c] = 1 iff V accepts given that P* has random string ω and verifier has random string c c ω 1 1 Fraction ε of entries are 1 1 1 There exists a row with two 1 -s iff ε > κ : = 1 / |{c}| 1

GENERAL K If P* makes V to accept with prob. ε > κ, K does: 1 / ε expected steps 1. Generate random (ω, c) until V accepts the resulting view (a, c, z) 2. Generate random c* (but use the same ω) until V c accepts the resulting view (a, 47 c*, z*)6 5 2 3. If c = c* then goto 1 Happens with some prob. p ω 1 / ε expected steps 2 1 35 4 6 4. Now K has (a, c, z), (a, c*, z*), with c ≠ 3 c*, and can 1 retrieve witness as before Tprobes : = the number of probed matrix entries before this happens 2 / (pε) expected steps

GENERAL Ε One has to analyze the number of expected number of steps Tprobes that guarantees that K will with high probability obtain such views Expected: with small probability, the number of steps can be very large Will omit precise analysis Answer: Tprobes = 2 / (ε - κ): expected number of runs

SPECIAL SOUNDESS: SIMPLIFIED Due to what we saw on last slides, we can somewhat simplify the special soundness definition We know the relation between ε - κ and the running time of extractor We can just assume that if we have already found two accepting views (a, c, z), (a, c*, z*) with c ≠ c*, then K can efficiently retrieve the witness We can then use what we know to construct full extractor

SPECIAL SOUNDNESS: SIMPLIFIED Definition (simplified) A Σ-protocol (P, V) is specially sound, if there exists a (deterministic) poly-time extractor algorithm K that, given two accepting views (a, c, z) and (a, c*, z*), such that c ≠ c*, can efficiently compute the value of the witness

GI: PROOF OF SPECIAL SOUNDNESS input = (G₁, 1. G₂) Generate random witness = φ isomorphism ψ 2. H ← ψ(G₁) input = (G₁, G₂) H c 1. If c = 1 then σ ← ψ 2. else σ ← ψ · φ ⁻ ¹ σ 1. c ← {1, 2} 1. If H = σ(Gc) then accept 2. else reject Construction of extractor: Given accepting views (H, c, σ) and (H, c*, σ*) with c ≠ c*, K outputs φ ← (σ*)⁻¹ ·σ Analysis: 1. Since H is the same and both views accept, H = σ(G₁) =σ*(G₂) 2. Thus φ is an isomorphism between G₁ and G₂

IDEA OF SHVZK input = (G₁, 1. G₂) Generate random witness = φ isomorphism ψ 2. H ← ψ(G₁) input = (G₁, G₂) H c 1. c ← {1, 2} σ 1. If c = 1 then σ ← ψ 2. else σ ← ψ · φ ⁻ ¹ ZK (idea, imprecise): Verifier only sees a random isomorphic copy of G₁, and an isomorphism from this copy to Gc. Intuitively no information leaked 1. If H = σ(Gc) then accept 2. else reject

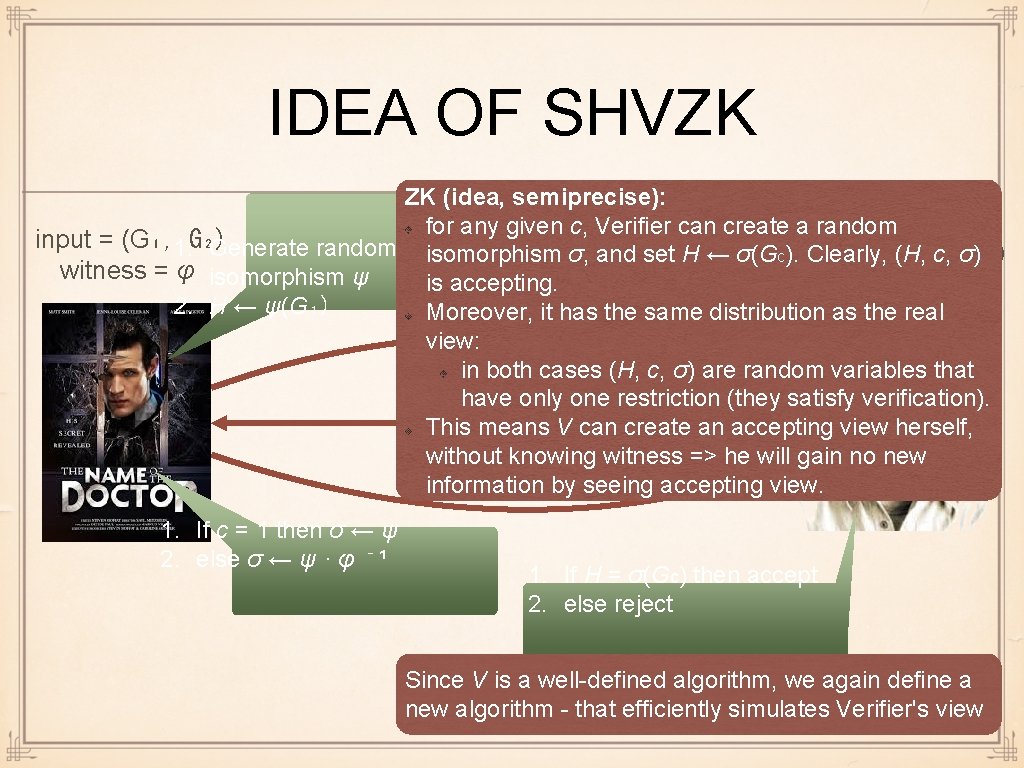
IDEA OF SHVZK ZK (idea, semiprecise): for any given c, Verifier can create a random input = (G₁, 1. G₂) Generate random isomorphism σ, and set H ← σ(Gc). Clearly, c, σ)G₂) input =(H, (G₁, witness = φ isomorphism ψ is accepting. 2. H ← ψ(G₁) H it has the same distribution as the real Moreover, view: in both cases (H, c, σ) are random variables that 1. c ← {1, (they 2} satisfy verification). haveconly one restriction This means V can create an accepting view herself, without knowing witness => he will gain no new σ by seeing accepting view. information 1. If c = 1 then σ ← ψ 2. else σ ← ψ · φ ⁻ ¹ 1. If H = σ(Gc) then accept 2. else reject Since V is a well-defined algorithm, we again define a new algorithm - that efficiently simulates Verifier's view

FORMALLY: SHVZK Definition A Σ-protocol (P, V) is SHVZK, if there exists a probabilistic poly-time simulator algorithm S that can, for any c, generate first a random z, and then a suitable a, such that 1. (a, c, z) accepts, and 2. if c is random then (a, c, z) has the same distribution as the real protocol views S must have a "superpower": otherwise dishonest prover could also simulate the view. Here the superpower is out-of-order execution

SHVZK: COMMENTS SHVZK is both stronger and weaker than "zero-knowledge" Weaker: It is honest verifier. It only guarantees ZK against a verifier that chooses c randomly and independently of a Stronger: It is special. It allows to simulate the view by using very strict well-defined algorithm We will make us of both "specials" (soundness, ZK) in following lectures to construct interesting protocols

SECURITY AMPLIFICATION In practice κ = 1 / 2 is way too big Simple solution: run the same protocol in parallel s times If P honest: honest V accepts always Completeness and ZK clearly carry over If P dishonest: the probability that V accepts in all runs is κˢ = 2⁻ ˢ Universal remedy, however it makes protocol slower It is better to start with smaller κ before the amplification

WHY Σ-PROTOCOLS? Security definitions correspond to intuition behind a very natural protocol Can construct efficiently for many problems Halfway there: soundness against malicious prover, zero-knowledge against honest verifier Can get, by adding a few extra steps, get a four-message ZK out from any Σ-protocol in a black-box way: it does not depend much on the concrete Σ-protocol Since we know how to construct Σ-protocols for NP-complete protocols (see Hamiltonian path in last slides), this means we can construct four-message ZK protocols for any language in NP

STUDY OUTCOMES Reminder: ZK Example, very natural, protocol with "intuitive" security Σ-protocols: definition Motivations behind definition For example: why special soundness? (from natural protocol)

NEXT LECTURE Σ-protocols based on DL For example: knowledge of DL (knowledge of Elgamal sk) Various stuff about Elgamal plaintexts For example: Σ-protocol that Elgamal plaintext is in {0, 1}

TUTORIAL The following material is presented in tutorial It may be required for exam!

HAMILTONIAN PATH A Hamiltonian path in graph G is a path that visits every vertex exactly once Hamiltonian cycle: HP that is a cycle HP problem: does Hamiltonian path exist in this graph? Known to be NP-complete

QUIZ: HAMILTONIAN PATH Question: Does HC or at least HP exist in this graph? If not, how many edges would you need to add to get HP/HC?

ANSWER: HAMILTONIAN PATH Question: Does HC or at least HP exist in this graph? If not, how many edges would you need to add to get HP/HC? Answer: Previous graph has HP but no HC. It suffices to add one edge to get HC

QUIZ: Σ-PROTOCOL FOR HP Assume Prover knows Hamiltonian path in G Question: How can Prover convince Verifier in this? Hint: use the fact we can solve GI

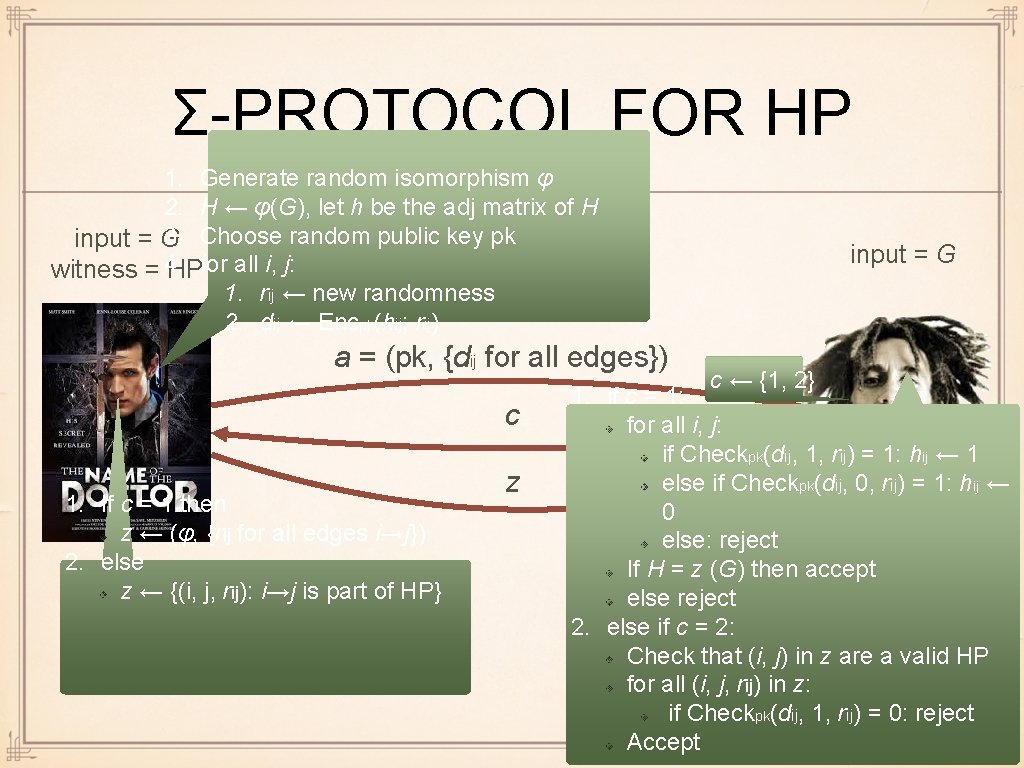
ANSWER: Σ-PROTOCOL FOR HP Prover creates a random isomorphic copy H of G, and sends to Verifier its encrypted edges Actually "committed" (see lecture 13) Checkpk (d, a, r): Verifier selects random c 1. if Encpk (a, r) = d return If c = 1: P reveals H and the isomorphism 1 2. else return 0 If c = 2: Prover opens encrypted edges of H that correspond to HP. Verifier checks this opening is correct Honest Prover succeeds always If G has no Hamiltonian path, Prover fails with probability 1/2

Σ-PROTOCOL FOR HP 1. Generate random isomorphism φ 2. H ← φ(G), let h be the adj matrix of H 3. Choose random public key pk input = G witness = 4. HPfor all i, j: 1. rij ← new randomness 2. dij ← Encpk(hij; rij) a = (pk, {dij for all edges}) c 1. If c = 1 then z ← (φ, {rij for all edges i→j}) 2. else z ← {(i, j, rij): i→j is part of HP} z input = G c ← {1, 2} 1. if c = 1: for all i, j: if Checkpk(dij, 1, rij) = 1: hij ← 1 else if Checkpk(dij, 0, rij) = 1: hij ← 0 else: reject If H = z (G) then accept else reject 2. else if c = 2: Check that (i, j) in z are a valid HP for all (i, j, rij) in z: if Checkpk(dij, 1, rij) = 0: reject Accept

TASK prove security of this protocol!